A Boosting Fuzzy Clustering Technique for Image Segmentation based on an Initial Low-Class

Abstract

Image segmentation is a basic problem in medical image analysis and useful for disease diagnosis. However, the complexity of medical images makes image segmentation difficult. In recent decades, fuzzy clustering algorithms have been preferred due to their simplicity and efficiency. However, they are sensitive to noise. To solve this problem, many algorithms using non-local information have been proposed, which perform well but are inefficient. This paper proposes a boosting fuzzy clustering algorithm utilizing non- local self-similarity and a low-class prior for image segmentation. Firstly, cluster centers are initialized based on peak detection. Then, a pixel correlation model between corresponding pixels is constructed, and similar pixel sets are retrieved. To improve efficiency and robustness, the proposed algorithm uses a novel objective function combining non-local information and an initial low-class. The algorithm\'s ability to achieve satisfactory results while simultaneously significantly increasing efficiency is demonstrated by experiments on medical and synthetic images.

Introduction

I. INTRODUCTION

With the development of medical diagnostic technology, various forms of information, such as medical images and electrocardiograms, have been adopted for use in clinical decision support systems. The combination of medical knowledge and data processing technology is an active research area which has received extensive attention. Currently, data processing technologies such as image segmentation, image registration, and 3D reconstruction play an important role in smart healthcare [1]. Generally speaking, medical image segmentation can be used to partition an image into di?erent tissues or organs, which is helpful for clinical decision support systems. However, the complexity of medical images makes this problem di?cult. In medical images, the intensity value of a pixel is in?uenced by adjacent pixels due to the imaging principle [2]. Therefore, the intensity value of a pixel may represent interactions with corresponding tissues or organs. Many algorithms have been proposed for image segmentation, such as threshold-based algorithms [3– 5], fuzzy clustering algorithms [6], and so on. Among these algorithms, fuzzy C-means (FCM) is preferable since it is suitable for modeling the principles of formation of medical images. In FCM, each pixel is assigned membership in [0, 1] to denote the degree to which it concurrently belongs to each of several clusters. Much information is thereby retained, enhancing the segmentation results.

However, the traditional FCM algorithm is sensitive to image noise as it only considers intensity information; many algorithms have been proposed to improve its robustness.   For example, Bezdek [7] proposed a bias-corrected version of FCM (BCFCM), and Stelios [8] proposed a fuzzy local information C-means clustering algorithm (FLICM). In these algorithms, neighborhood information is introduced in di?erent forms to improve performance. However, when the image is contaminated heavily, these algorithms are either ine?ective or ine?cient.

To achieve satisfactory results, improved FCM algorithms based on non-local information (NLFCM) have been proposed [9]. In NLFCM, the information covering the whole image can be utilized, and is not limited to the vicinity of a given pixel. In algorithms such as BCFCM, FLICM, and NLFCM, neighboring pixels or similar pixels are made to belong to the same cluster, thus improving the insensitivity to image noise. In these algorithms, the most important problem is to measure the relatedness of pixels, which can be measured in di?erent ways. In Ref. [7], the pixel correlation between neighboring pixels and the central one is de?ned as the constant α. In Ref. [10], pixel relatedness is de?ned as the product of spatial relatedness and intensity relatedness. Due to the limitations of spatial relatedness, pixel relatedness decreases greatly with the increase of Euclidean distance between pixels. Thus, only nearby pixels can play positive roles, resulting in poor performance. In Ref. [9], pixel relatedness is de?ned as the similarity between image patches, which can enhance the results to some extent, but with low e?ciency.

This paper proposes an improved fuzzy clustering algorithm for segmentation, exploiting more information.   Firstly, the cluster centers are initialized by peak detection. Then, a novel distance model to measure pixel relatedness is constructed, a patch weighted distance. With accurate relatedness, more information can be utilized, just as in NLFCM. Finally, a low-class prior is merged into the fuzzy clustering algorithm framework to perform image segmentation.

The rest of the paper is organized as follows: Section 2 presents the motivation and contribution. Section 3 presents the proposed algorithm in detail, including cluster center initialization, a novel pixel relatedness model, and the improved fuzzy clustering algorithm. Section 4 shows and analyses experimental results and Section 5 Conclusion of the paper.

II. MOTIVATION AND CONTRIBUTION

In improved FCM algorithms based on non-local information, to ensure e?ciency, a search window with a large radius is adopted instead of the whole image. In essence, the purpose of these methods is to enforce similar pixels to be classi?ed as belonging to the same cluster. However, the improved robustness comes at the cost of e?ciency [9].   Speci?cally, if the radius of the search window is r, the number of pixels considered in image segmentation is (2r + 1)2- 1 . When the patch-weighted distance model is introduced to measure pixel relatedness, (2r + 1)2- 1  weights must be computed ?rst, which further reduces e?ciency. To overcome this problem, this paper proposes a segmentation method based on a low-class prior and non-local self-similarity.

As we all know, almost all images have high information redundancy either in the form of low class or sparse representation [11, 12]: many pixels share similar features.   Based on a low-class prior or sparse representation, images can be denoised [13–17]. For medical images with limited intensity levels, the phenomenon of low class is particularly obvious. Figure 1 illustrates the low-class property using two medical images. The patch matrices are approximately low-class, so most image patches share similar features. Therefore, in the image segmentation process, we can improve the e?ciency by putting those similar pixels into the same cluster without considering dissimilar pixels.

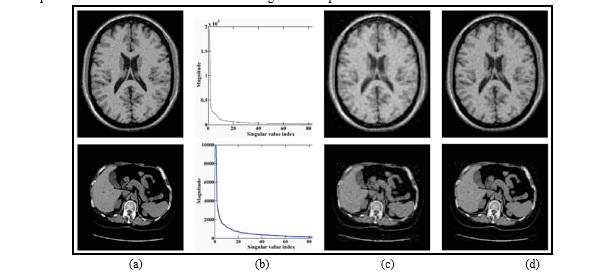
Fig.1 Low-class prior in medical images. (a) Original images (above: MR brain image, below: CT lung image). (b) Distributions of singular values of corresponding patch matrices. (c, d) Low-class approximations with class = 20, 30, respectively.

In fact, the idea of a low-class prior is widely applied in the ?elds of image denoising [13] and resolution enhancement [18]. In Ref. [19], an improved super pixel segmentation algorithm was proposed which updates the seeds by averaging pixels with the most homogeneous appearance; not all pixels belong to a super pixel. This can also avoid inhomogeneous intensity within a super pixel. In Ref. [18], a low-class prior is exploited to estimate the missing pixels and reconstruct the high resolution (HR) image. In segmentation algorithms based on soft sets [20], pixels are divided into three regions: positive, boundary, and negative. In the process of image segmentation, only the pixels in the positive and boundary regions are utilized.

Furthermore, fuzzy clustering algorithms tend to fall into local a minimum, which also reduces e?ciency. It is well known that the histogram of an image can re?ect its grayscale frequency distribution well [21], and many segmentation algorithms based on histograms have been proposed [22, 23]. Peaks in the histogram are grayscales correlated with more pixels while troughs are gray levels associated with fewer pixels. Generally speaking, the peaks are close to the cluster centers while the valleys lie far away. Therefore, the histogram peaks can be adopted for cluster initialization.

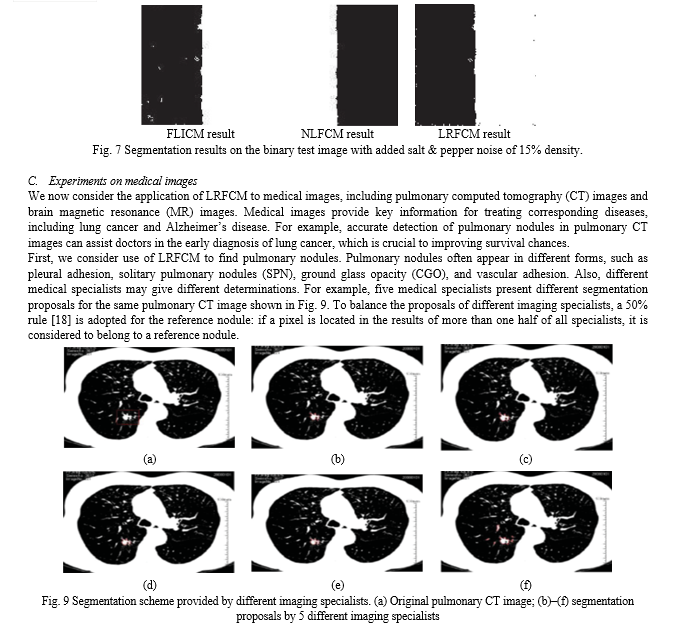
Recently, background knowledge or prior knowledge has been adopted in supervised algorithms, such as CNN-based methods, to improve accuracy [24]. However, these algorithms may provide highly inaccurate results for medical images for two reasons. First, there is physiological variability between di?erent subjects [25]. Secondly, large numbers of samples are required to train a CNN, which is di?cult due for individual privacy and other reasons. In clinical applications, accuracy and speed requirements of medical image segmentation are very high [26]. In order to achieve satisfactory results with acceptable e?ciency, we combine non-local information and a low-class prior in the framework of fuzzy clustering algorithms. Image segmentation proceeds in four steps: (i) initialize the cluster centers by peak detection, (ii) relatedness of pixels is modeled, (iii) a low-class prior is exploited to retrieve the most related pixels, and (iv) image segmentation is performed in the framework of fuzzy clustering.

Our main contributions are as follows: (i) an initialization method which avoids the local minimum problem of traditional fuzzy algorithms, (ii) a model which can accurately measure pixel relatedness, (iii) an e?cient yet e?cacious method for medical image segmentation, utilizing a low-class prior and non- local information simultaneously, and (iv) utilization of the FLICM framework, which is free of parameter adjustment and provides easy extension to other fuzzy clustering algorithms.

III. METHOD

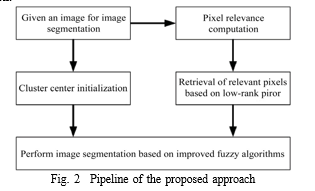
The framework of the proposed algorithm is presented in Fig. 2. It has three steps: cluster center initialization, related pixel retrieval, and image segmentation.

A. Cluster Center Initialization

In traditional fuzzy algorithms, memberships are initialized at random, and cluster centers are computed based on intensity values and initial memberships. In fuzzy clustering algorithms, random initialization of the memberships may lead to unstable performance, and often the process becomes trapped in local minima [27]. Intuitively, cluster centers should be located in regions with greater diversity: grayscales with higher frequency are suitable for use as the initial cluster centers. In the proposed schema, the cluster centers are initialized using peak detection [2].

B. Pixel relatedness model

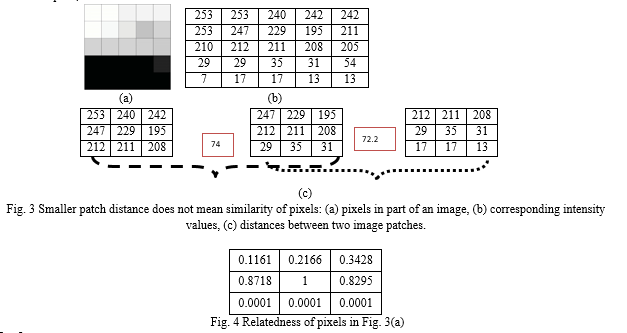
As mentioned earlier, the measurement of pixel relatedness is a key problem in fuzzy clustering algorithms. In our opinion, only considering the most closely related pixels in image segmentation will improve efficiency. In previous work [6, 9], pixel relatedness was measured by patch distance. However, a smaller distance between corresponding patches does not always correspond to similarity of pixels, as shown by the example in Fig. 3. It is reasonable to classify the center pixel and the pixel above in Fig. 3(a) in the same cluster, while the center pixel and the pixel below should belong to di?erent clusters. However, the distances suggest the opposite: see Fig. 3(c). Hence, measuring pixel relatedness by the distance between image patches is an unsuitable approach.

The problem is that distance between corresponding patches does not consider edge information. Specifically, di?erent neighbors of a pixel may have di?erent in?uences on the central pixel. To tackle this problem, we present a novel relatedness model, formalized in Algorithm 1, which introduces weighting for di?erent directions to better measure pixel relatedness. Using the novel model, the pixel relatedness between the center pixel and neighboring pixels in Fig. 3(a) is presented in Fig. 4. The relatedness computed by the novel model is more reasonable.

C. Finding related pixels by low-class prior

As mentioned      earlier,   information  from  a neighborhood or the whole image is used to resist the effects of image noise. More information provided by similar pixels plays a positive role in accurate performance. However, using more information reduces efficiency. To ensure efficiency, various limitations have been considered. For example, the size of the search window may be limited, and only neighboring pixels are considered in FGFCM and FLICM. In NLFCM, a large search window is used, including similar and dissimilar pixels. Since only similar pixels play a positive role, why not neglect the dissimilar pixels?

When image patches are analyzed by singular value decomposition (SVD), most of the energy is concentrated into a few, largest, singular values. Following denoising algorithms [14, 15], we utilize the most related pixels to play a positive role in image segmentation, while neglecting other pixels in the non-local search window. As we all know, the reason for the success of low class and sparse representations is that many pixels in the image share similar features [28]. Therefore, the number of pixels in a cluster is closely related to the class of image patches. Speci?cally, a large class means a small number of pixels in the same cluster, while a low class means a large number of pixels in the same cluster. However, measuring the class accurately is very difficult, and considering fewer pixels will degrade accuracy.   Hence, we must consider the number of similar pixels in the search window based on the class prior, which will be discussed in Section 4.

D. Image segmentation

We now present the improved FLICM algorithm in detail. FLICM introduces a fuzzy factor to replace the e?ects of neighboring pixels, and avoids the burden of parameter adjustment. However, when applied to complex images, FLICM has the following disadvantages: (i) when the image is severely noisy, FLICM performs poorly, (ii) the relatedness between pixels is measured by Euclidean distance, so e?ectively ignores far away pixels, and (iii) to improve robustness, a large search window is used, degrading e?ciency. We aim to overcome these problems, using non-local information and a low- class prior to achieve high accuracy with acceptable e?ciency. In this study, the fuzzy factor is de?ned as

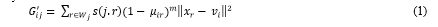
Conclusion

In this study, an improved algorithm for image segmentation is proposed, which combines non-local information and a low-rank prior into the framework of fuzzy clustering. In the proposed algorithm, a novel pixel relatedness model is presented, by which non-local information can be utilized to improve the robustness. With the help of a low-class prior, only the information provided by the most similar pixels is utilized, which improves the efficiency of our algorithm based on non-local information. Experiments on synthetic and medical images illustrate the advantages of the proposed algorithm over other FCM-related algorithms. In our future work, the ideas of this study will be extended to medical image series segmentation. Relatedness will be measured by similarity within pixel cubes, to utilize information covering the whole image series.

References

[1] Liu, H.; Xu, J.; Wu, Y.; Guo, Q.; Ibragimov, B.; Xing, L. Learning deconvolutional deep neural network for high resolution medical image reconstruction. Information Sciences Vol. 468, 142–154, 2018. [2] Zhang, X. F.; Zhang, C. M.; Tang, W. J.; Wei, Z. W. Medical image segmentation using improved FCM. Science China Information Sciences Vol. 55, No. 5, 1052–1061, 2012. [3] Orduna, R.; Jurio, A.; Paternain, D.; Bustince, H.; Melo-Pinto, P.; Barrenechea, E. Segmentation of color images using a linguistic 2-tuples model. Information Sciences Vol. 258, 339–352, 2014. [4] Chaira, T. A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Applied Soft Computing Vol. 11, No. 2, 1711– 1717, 2011. [5] Verma, H.; Agrawal, R. K.; Sharan, A. An improved intuitionistic fuzzy C-means clustering algorithm incorporating local information for brain image segmentation. Applied Soft Computing Vol. 46, 543– 557, 2016. [6] Zhang, X. F.; Guo, Q.; Sun, Y. J.; Liu, H.; Wang, G.; Su, Q. T.; Zhang, C. M. Patch-based fuzzy clustering for image segmentation. Soft Computing Vol. 23, No. 9, 3081–3093, 2019. [7] Ahmed, M. N.; Yamany, S. M.; Mohamed, N.; Farag, A. A.; Moriarty, T. A modi?ed fuzzy C-means algorithm for bias ?eld estimation and segmentation of MRI data. IEEE Transactions on Medical Imaging Vol. 21, No. 3, 193–199, 2002. [8] Krinidis, S.; Chatzis, V. A robust fuzzy local information C-means clustering algorithm. IEEE Transactions on Image Processing Vol. 19, No. 5, 1328– 1337, 2010. [9] Zhang, X. F.; Sun, Y. J.; Wang, G.; Guo, Q.; Zhang, C. M.; Chen, B. J. Improved fuzzy clustering algorithm with non-local information for image segmentation. Multimedia Tools and Applications Vol. 76, No. 6, 7869– 7895, 2017. [10] Cai, W. L.; Chen, S. C.; Zhang, D. Q. Fast and robust fuzzy C-means clustering algorithms incorporating local information for image segmentation. Pattern Recognition Vol. 40, No. 3, 825–838, 2007. [11] Zhang, F.; Li, J. J.; Liu, P. Q.; Fan, H. Computing knots by quadratic and cubic polynomial curves. Computational Visual Media Vol. 6, No. 4, 417–430, 2020. [12] Liu, X. X.; Zhang, Y. F.; Bao, F. X.; Shao, K.; Sun, Z. Y.; Zhang, C. M. Kernel-blending connection approximated by a neural network for image classi?cation. Computational Visual Media Vol. 6, No. 4, 467–476, 2020. [13] Guo, Q.; Zhang, C. M.; Zhang, Y. F.; Liu, H. An e?cient SVD-based method for image denoising. IEEE Transactions on Circuits and Systems for Video Technology Vol. 26, No. 5, 868–880, 2016. [14] Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing Vol. 15, No. 12, 3736–3745, 2006. [15] Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative ?ltering. IEEE Transactions on Image Processing Vol. 16, No. 8, 2080–2095, 2007. [16] Dong, W. S.; Lei, Z.; Shi, G. M.; Wu, X. L. Nonlocal back-projection for adaptive image enlargement. In: Proceedings of the 16th IEEE International Conference on Image Processing, 349–352, 2009. [17] Ma, D. Y.; Zhou, Y. F.; Xin, S. Q.; Wang, W. P. Convex and compact superpixels by edge-constrained centroidal power diagram. IEEE Transactions on Image Processing Vol. 30, 1825–1839, 2021. [18] Liu, H.; Guo, Q.; Wang, G. L.; Gupta, B. B.; Zhang, [19] C. M. Medical image resolution enhancement for healthcare using nonlocal self-similarity and low-rank prior. Multimedia Tools and Applications Vol. 78, No. 7, 9033–9050, 2019. [20] Zhang, Y. X.; Li, X. M.; Gao, X. F.; Zhang, C. M. A simple algorithm of superpixel segmentation with boundary constraint. IEEE Transactions on Circuits and Systems for Video Technology Vol. 27, No. 7, 1502– 1514, 2017. [21] Namburu, A.; Samay, S. K.; Edara, S. R. Soft fuzzy rough set-based MR brain image segmentation. Applied Soft Computing Vol. 54, 456–466, 2017. [22] Kim, G. R.; Kim, E. K.; Kim, S. J.; Ha, E. J.; Yoo, J.; Lee, H. S.; Hong, J. H.; Yoon, J. H.; Moon, H. J.; Kwak, [23] J. Y. Evaluation of underlying lymphocytic thyroiditis with histogram analysis using grayscale ultrasound images. Journal of Ultrasound in Medicine Vol. 35, No. 3, 519–526, 2016. [24] Otsu, N. A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man, and Cybernetics Vol. 9, No. 1, 62–66, 1979. [25] Ben Ishak, A. A two-dimensional multilevel thresholding method for image segmentation. Applied Soft Computing Vol. 52, 306–322, 2017. [26] Liu, Y.; Cheng, M. M.; Hu, X. W.; Bian, J. W.; Zhang, L.; Bai, X.; Tang, J. Richer convolutional features for edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol. 41, No. 8, 1939–1946, 2019. Singh, C.; Bala, A. A DCT-based local and non-local fuzzy C-means algorithm for segmentation of brain magnetic resonance images. Applied Soft Computing Vol. 68, 447–457, 2018. [27] Ren, T. B.; Wang, H. H.; Feng, H. L.; Xu, C. S.; Liu, G. S.; Ding, P. Study on the improved fuzzy clustering algorithm and its application in brain image segmentation. Applied Soft Computing Vol. 81, 105503, 2019. [28] Pham, T. X.; Siarry, P.; Oulhadj, H. Integrating fuzzy entropy clustering with an improved PSO for MRI brain image segmentation. Applied Soft Computing Vol. 65, 230–242, 2018. [29] Guo, Q.; Gao, S. S.; Zhang, X. F.; Yin, Y. L.; Zhang, C. M. Patch-based image inpainting via two-stage low rank approximation. IEEE Transactions on Visualization and Computer Graphics Vol. 24, No. 6, 2023–2036, 2018. [30] Szila´gyi, L. Lessons to learn from a mistaken optimization. Pattern Recognition Letters Vol. 36, 29–35, 2014. [31] Krinidis, S.; Chatzis, V. A robust fuzzy local information C-means clustering algorithm. IEEE Transactions on Image Processing Vol. 19, No. 5, 1328– 1337, 2010. [32] Kwan, R. K. S.; Evans, A. C.; Pike, G. B. MRI simulation-based evaluation of image-processing and classi?cation methods. IEEE Transactions on Medical Imaging Vol. 18, No. 11, 1085–1097, 1999.

Copyright

Copyright © 2023 C. Ramesh, Dr. T. Venugopal. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.