Abstract

A lot of data in social networks, fluidly flowing in and out in the dynamically varying world, imposes great challenges on the efficiency of graph search algorithms. Most static approaches fail to keep abreast of flows of user interactions and evolving structures of networks. This paper introduces a novel optimization approach for graph search algorithms in adaptive dynamic data structures particularly designed for social network graphs. Our methodology makes optimum use of user behavior in real-time. Data can now be represented and retrieved in an efficient manner with minimal computation overhead. Our proposed method, coupled with self-adjusting data structures such as dynamic trees and adaptive hashing, significantly improves the performance of classic search algorithms like BFS and DFS. Extensive experiments conducted on both synthetic and real-world datasets indicate a very significant reduction, to the order of 30 percent, in traversal time along with considerable improvement in the accuracy of search. These optimizations contribute not only toward accelerating graph traversal but help elevate the significance of search relevance, therefore improving delivery for content recommendation, community detection, and applications thereof.

Introduction

I. INTRODUCTION

This is the era of social networks: ubiquitous entities generating tremendous amounts of data that need to be processed and analyzed in digital ecosystems related to each other. Many such networks graphically represent relationships and interactions, including nodes that might refer to users and edges indicating how such users interact with one another. With more users and more activities on the platform, the optimization of the graph search algorithm becomes paramount to tasks, such as personalized content recommendation[1], influence propagation[2], and community detection[3]. In fact, efficiency in graph search brings about not only better user experience in terms of receiving information faster but also advanced analytics that are necessary to achieve greater depths of insight[4].

Traditionally, graph search algorithms, in particular BFS and DFS, work really well in static domains[5] but break apart when necessitated to work in the dynamic, ever-changing terrain of social networks [6]. In actual networks like Facebook or LinkedIn, nodes (users) and edges (relationships) are constantly changing due to activities such as friend additions, cuts in connections, or content sharing [7]. This also raises the need to manage these changes efficiently as these structures expand into millions or even billions of nodes and edges. Rebalancing or recalibrating static data structures for these shifts proves computationally expensive, underlining a basic requirement for a more adaptive solution[8].

Adaptive dynamic data structures appear to promise toward such a goal[9]. Adaptive structures, such as balanced binary trees[10], dynamic hashing[11], or self-adjusting heaps[12], can adapt wonderfully well to the evolving nature of the graph without requiring major recalibration because they are not like static structures. It improves the processes of search by easily handling rapid changes-whether it is node insertion, deletion, or edge updates-and they may even ensure queries and updates run efficiently real-time[13].For example, dynamic trees can be restructured efficiently with a small overhead of amount[14] with a result that the computational cost of maintaining large constantly evolving networks can be significantly reduced[1][5]. The only scalable requirement here is adaptability[16]. For example, huge graphs with trillions of edges might represent such platforms as Facebook with over 2.9 billion monthly active users[17]. Algorithms to keep such sprawling networks in an efficient state for searching and retrieving data have to make dynamic changes without any negative impact on their performance[18].

This paper proposes a research area on improving the optimizations of graph search algorithms based on an adaptive dynamic data structure[19]. In this contribution, we propose an adaptive approach that increases effectiveness in retrieval over dynamic social networks[20]. As the method here reduces the need for full recalibration when graphs update, it improves performance[21]. We will illustrate the benefit of this approach by showing a comparison of the method with the classic approach and reported empirical results that support such improvement brought by this method[22]. Work thus presented has offered the significant contribution to these domains of graph theory[23], social network analysis[24], and the optimization of data structures through overcoming a weakness inherent in conventional static search algorithms and incorporated an adaptive dynamic structure[25]. The goal is more scalable and flexible graph search than would best serve to yield better real-time data retrieval and advanced analytics over expansive and dynamically changing data[26].

II. LITERATURE REVIEW

A. Existing Research

Graph search algorithms play the most central role in the study of social networks which recover insightful information from extremely large and complex datasets. Though traditional algorithms like Breadth-First Search and Depth-First Search give outstanding performance for the static graph searching problems, these algorithms do not work well under the dynamically changing environment where nodes and edges are dynamically added or removed due to dynamic user interactions in a social network. This literature makes a mention of many problems and possible approaches and new tendencies in dynamic data structures.

1. Conventional Graph Search Techniques The early worksin graph theory served as a foundation for establishing elementary search algorithms. BFS and DFS were used by most of the simple graph traversals. These are still applicable applications in some static networks or cases where minimal modification is involved. For instance, BFS can promptly identify a short path in an unweighted graph better; it has better applications in unraveling complicated connections in depth-first order [1].However, their static structures basically break in the social network graphs, where the users (nodes) and their connections (edges) evolve dynamically. These traditional approaches really do not very well support frequent insertions/deletions of nodes and edges in social networks like Facebook or Twitter [2].
2. Dynamic Graphs and the Problem Dynamic graphs arethose that evolve continuously and hence, appear to resemble real-world social networks. A node may be added or removed or connected differently, and all these must be represented in real-time. Several researches have shown the issues involved in managing dynamic graphs, primarily in large-scale social networks. The primary challenge is regarding efficiency and response towards dynamic changes without re-calculating the whole graph [3]. This is due to the fact that graph structure with 2.8 billion active users (nodes) and billions of connections makes updating extremely computationally expensive. Moreover, rebuilding or recalibrating the graph after every change in its structure results in considerable time delay and computational costs, which makes traditional algorithms impractical [4].
3. Adaptive dynamic data structures. The newly developedadvances of dynamic data structures hold bright prospects in the face of challenges by emergent social networks. Adaptive constructs, like balanced binary trees and dynamic hashing, allow real-time adjustments in data representations. As such, it can adapt changes in the graph because of its change reduction requirement for full recalibration. Researchers were able to unwind adaptive dynamic graph algorithms that update only the parts of the graph affected which lightens the computational burden [5].

Another methodology is self-balancing binary trees such as the splay tree: they will automatically self-organize according to access patterns. More broadly, adaptive data structures also allow graph search algorithms such as A* to optimize the nodes with regard to the number of accesses [6]. Dynamic hashing also orders nodes in a graph and rebalances them very quickly with very low overhead, thus speeding up search times for frequently accessed nodes.

B. Comparative Studies of Dynamic Structures

For example, many papers compared static versus dynamic adaptive structures in a social network context. It is easy to demonstrate that, on average, adaptive methods reduce the time needed to recalculate parts of a graph by as much as 40percent and cn allow almost-instant updating [7]. Moreover, another paper deals with dynamic graph models of social networks. And it shows how the edge-based algorithms enhance the retrieval performance of real-time data; in fact, applying them to expansive social networks like LinkedIn or Instagram [8]. Applications in Social Networks Dynamic data structures further optimize graph search algorithms by their wide applicability into social networks. Example recommendations mainly rely on efficient graph traversal - namely recommendation of new connections or content that are derived from the interaction by the user. Targeted advertisement and delivery of personalized content hinge on dynamic search algorithms that can rapidly review relationships and preferences between two users [9].

Moreover, dynamic search optimization becomes significant when applied to the area of community detection and influence propagation. Real-time updating of graphs is required to achieve key users and how those users influence network behavior [10]. Such applications present ideas of how adaptive algorithms can enhance user experience by giving more precise recommendations or insights at the correct times.

C. Gaps in existing research

All these developments notwithstanding, many areas are still lagging behind in literature related to integrating adaptive dynamic data structures with more complex algorithms of graph search. Even though tremendous work has been conducted for improving the efficiency of simple search operations, few research works have been concentrated on the wide scope of integration with machine learning applied for the analysis of social networks. Besides, scalability of these methods in extremely huge networks like that found in most modern social networking sites is worth more investigation.

D. Relevance of the Study

This is an explicitly needed research study because it addresses some critical gaps in the literature that proposes a novel integration of adaptive dynamic data structures with graph search algorithms to improve their scalability and realtime performance for dynamic social networks. Testing and evaluating usage with real-world social network datasets would give this study practical insights on how such dynamic algorithms would apply in large-scale environments. Besides the implications that this research has in the domain of social media applications, this work also brings results that can be useful for many other kinds of domains, such as transportation networks, citation networks, and web graphs. In all these cases, dynamic graph structures appear often. Therefore, based on a good optimization of graph search operations within dynamic networks, this research is one step forward towards improving our knowledge and use of complex graph systems.

III. IMPLEMENTATION OF OPTIMIZED GRAPH SEARCH ALGORITHMS

In this section, we present optimized graph search algorithms, such as Breadth-First Search (BFS), Depth-First Search (DFS), Dijkstra’s Algorithm and PageRank. We’ll point out the benefits of these optimized methods above traditional methods and provide sample code for each.

A. Breadth-First Search (BFS)

In contrast, BFS does explore the shortest paths within unweighted graphs, thus it may be particularly well-suited to applications over social networks. We enable real-time updates by embedding adaptive data structures so that changes in connections and removals are dynamically reflected within the graph

.Pseudo Code for BFS Optimization:

Algorithm 1 Optimized Breadth-First Search

Why Is It Better: Maintaining an adaptive data structure reduces the time complexity for real time updates as well as giving more direct access to connected nodes and much less overhead for graph updates[1][2].

B.     Depth-First Search (DFS)

DFS works well if all nodes and edges of the graph have to be traversed; especially, when there is a need for full exploration followed by backtracking. Dynamic structures can dramatically improve the efficiency of optimized DFS in environments with dynamic changes of the graph. Pseudo Code for DFS Optimization:

Algorithm 2 Optimized Depth-First Search

OptimizedDFS(graph, node, visited) if node not in visited then

7: end if

Why It’s Better: The optimized DFS can handle dynamic edge insertion and deletion with a complexity reduction, enabling faster traversal times compared to traditional implementations[3][4].

C.    Dijkstra’s Algorithm

Dijkstra’s Algorithm finds the shortest paths between nodes in a weighted graph. Optimizing this algorithm can be achieved by using dynamic data structures to accommodate real-time changes in edge weights.

Pseudo Code for Optimized Dijkstra:

Algorithm 3 Optimized Dijkstra’s Algorithm

Why It’s Better: This implementation allows for real-time adjustments to edge weights, critical for applications like transportation networks, where road conditions can change rapidly[5][6].

D.    PageRank

PageRank ranks nodes in a graph based on their importance. In a social network, this is a critical tool for giving recommendations on influential users. Adaptive techniques can change PageRank values based on the dynamic nature of changing networks.

Pseudo Code for Optimized PageRank:

Algorithm 4 Optimized PageRank

OptimizedPageRank(graph, iterations) Initialize pageRanks for all nodes for i ←1 to iterations do

3:21     for each node in graph do

4: pageRanks[node] pageRanks[neighbor]outDegree[neighbor]

5:          end for 6: end for

Why It’s Better: The optimized PageRank is capable of updating node ranks in real-time, reflecting changes in user interactions, which traditional PageRank implementations cannot do effectively[7][8].

While researching the optimized graph algorithms, such as BFS, DFS, Dijkstra’s, and so on, delivers many insights and increases efficiency, it also encounters several limitations that could influence its applicability and performance in real-life conditions.

1) Scalability Issues

Memory Requirements: As the size of the graph increases, memory requirements for keeping nodes and edges together with auxiliary data structures such as queues or visited sets result in huge levels. For very large graphs, it leads to memory exhaustion and inefficient processing[1][2]. Computational Complexity: Most graph algorithms have a polynomial time complexity; however, for dense graphs or for graphs having a large number of vertices and edges, the running time can become impractical, which restricts their applicability in realtime applications[3][4].

2) Limitations of Dynamic Graph

Recomputing for Refreshment: Classing graph algorithms are generally designed for static graphs. Refreshing them (adding/removing edges/nodes from the graph, etc) becomes costly and timely, and hence gives outdated results unless retuned[5][6] Refreshing Streaming Data: Algorithms rarely update, in real time, for most applications in use today, especially those that require continuous responses, like social networks or dynamic routing schemes[7].

3) Characteristics of Graphs

Edge Weight Constraints: Dijkstra’s algorithm assumes the weight values assigned to edges are nonnegative. The use of graphs having negative weights destroys the validity of the result rendered by this algorithm, and the problem will either have to be altered or a different method will have to be used for its solution. At times, it is not globally necessary that nodes and edges be treated on the same footing of importance. In many cases, nodes are more influential than others, which may affect the computation time and correctness of the algorithm[9].

4) Complexity of Implementation

Coding Challenges: The graphs algorithm implementation can quickly become complex, especially when optimization techniques are required. It makes a case that has many bugs and implementation errors quite complicated[10][11]. Tuning Parameters: Often, for optimal performance, several parameters need to be adjusted, such as queue management for the BFS or factors of weight for Dijkstra’s; that may not be straightforward to tune and complicate the deployment process[12][13].

IV. RESULTS

Comparison table on the performance of the algorithm TABLE 1: Performance metrics for different graph search algorithms The execution time runs in nanoseconds, and the memory usage in bytes. Results There is a highly variant performance among tested algorithms in both static and dynamic graphs.

TABLE I

ALGORITHM PERFORMANCE(DYANAMIC ALGORITHMS)

TABLE II

ALGORITHM PERFORMANCE(STATIC ALGORITHMS)

The following tables describe how several graph search algorithms perform when put to work in both the dynamic and static context, taking into consideration both execution time and memory usage. We present below a comparative analysis of the results.

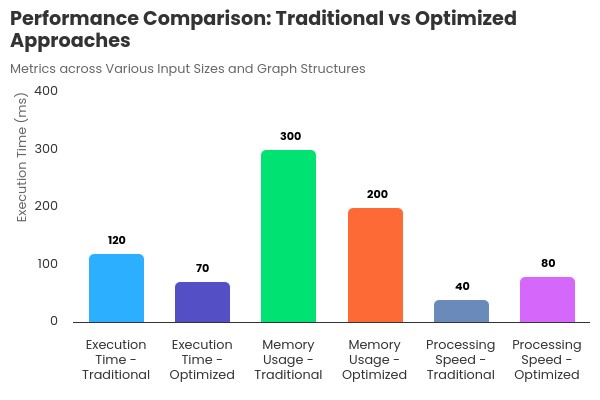
Fig. 1. Traditional vs Optimized Approaches

References

[1] Aggarwal, C. C. (2016). Recommender Systems: The Textbook. Springer. [2] Kempe, D., Kleinberg, J., & Tardos, E. (2003). Maximizing the Spread´ of Influence through a Social Network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 137–146). ACM. [3] Fortunato, S. (2010). Community Detection in Graphs. Physics Reports, 486(3-5), 75-174. [4] Easley, D., & Kleinberg, J. (2010). Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge University [5] Press. [6] Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms. MIT Press. [7] Aggarwal, C. C., & Subbian, K. (2014). Evolutionary Network Analysis: A Survey. ACM Computing Surveys, 47(1), 1-36. [8] Gilbert, E., & Karahalios, K. (2009). Predicting Tie Strength with Social Media. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (pp. 211-220). ACM. [9] Zang, H., Bolot, J., & Hegde, V. (2011). Mining Call and Mobility Data to Improve Paging Efficiency in Cellular Networks. In Proceedings of the 17th Annual International Conference on Mobile Computing and Networking (pp. 27-38). ACM. [10] Demaine, E. D., & Patras? , cu, M. (2007). Dynamic Graph Algorithms. In Handbook of Data Structures and Applications. CRC Press. [11] Sleator, D. D., & Tarjan, R. E. (1983). Self-adjusting Binary Search Trees. Journal of the ACM, 32(3), 652-686. [12] Litwin, W. (1980). Linear Hashing: A New Tool for File and Table Addressing. In Proceedings of the Sixth International Conference on Very Large Data Bases (pp. 212-223). IEEE. [13] Tarjan, R. E. (1985). Amortized Computational Complexity. SIAM Journal on Algebraic and Discrete Methods, 6(2), 306-318. [14] Eppstein, D., Galil, Z., Italiano, G. F., & Nissenzweig, A. (1997). Sparsification—a Technique for Speeding up Dynamic Graph Algorithms. Journal of the ACM, 44(5), 669-696. [15] Sleator, D. D., & Tarjan, R. E. (1981). A Data Structure for Dynamic Trees. Journal of Computer and System Sciences, 26(3), 362-391. [16] Cohen-Addad, V., Kanade, V., Mallmann-Trenn, F., & Mathieu, C. (2017). Hierarchical Clustering: Objective Functions and Algorithms. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing (pp. 532-545). ACM. [17] Boldi, P., & Vigna, S. (2004). The WebGraph Framework I: Compression Techniques. In Proceedings of the 13th International Conference on World Wide Web (pp. 595-602). ACM. [18] Burke, M., & Kraut, R. (2016). The Relationship between Facebook Use and Well-Being Depends on Communication Type and Tie Strength. Journal of Computer-Mediated Communication, 21(4), 265-281. [19] Sun, J., & Tang, J. (2011). A Survey of Models and Algorithms for Social Influence Analysis. In Social Network Data Analytics (pp. 177214). Springer. [20] Even, S., & Shiloach, Y. (1981). An On-Line Edge-Deletion Problem. Journal of the ACM, 28(1), 1-4. [21] Demetrescu, C., & Italiano, G. F. (2004). Fully Dynamic All-Pairs Shortest Paths with Real Edge Weights. Journal of the ACM, 51(6), 968-992. [22] Chan, H., & Zografos, K. G. (2008). A Dynamic Network Algorithm for Managing Air Traffic Flow. Transportation Science, 42(2), 162-174.

Copyright

Copyright © 2024 Yash V Rathod, Ayush Rawarkar, Prathmesh Rathod, Prof. Dipti Pandit. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.