Advancements and Comparative Analysis of Digital Signature Algorithms: A Review

Abstract

: Digital signatures have emerged as crucial cryptographic tools for ensuring the authenticity, integrity, and non-repudiation of electronic documents and transactions in the digital age. With the increasing reliance on electronic communication and the growing threat landscape, it is essential to have a thorough understanding of digital signature algorithms and their suitability for various security applications. This review paper provides a comprehensive analysis of digital signature algorithms, including RSA-based, elliptic curve-based, and post-quantum cryptographic algorithms. It explores the underlying principles, security features, and performance characteristics of each algorithm category. The paper discusses the security requirements that digital signatures aim to fulfill and examines the strengths, limitations, and real-world applications of RSA-based, elliptic curve- based, and post-quantum cryptographic algorithms. It presents a comparative evaluation of these algorithms, considering security factors, performance metrics, and suitability for different use cases. The paper also addresses recent developments in quantum-safe cryptography, standardization efforts, and emerging digital signature algorithms. Overall, it provides valuable insights for practitioners and researchers in the field of digital signatures and cryptography.

Introduction

I. INTRODUCTION

A digital communication or report's validity can be verified using a digital signature, which is a mathematical system. A recipient has reason to believe that a communication was created by a known sender and was not changed in transit if it bears a valid digital signature. Software distribution, financial transactions, and other situations where it's crucial to spot fraud or tampering typically utilise digital signatures. Internet has permeated every aspect of our daily lives. The word "security" is crucial in this context. If a severe attack takes place, it will impact vital functions including trade, transactions, and communication.Private key Cryptography is a type of encryption that often enables users to communicate privately without having prior knowledge of a shared secret key. This is accomplished by the use of two distinct cryptographic keys, a public key and a personal key. A private key functions similarly to the email password whereas a public key is similar to an email address. While the non-public key is kept a secret from everyone, the public key is supplied to the recipient [1].They are mathematically related.

Only the second key can be used to decode something that has been encrypted with the first, and vice versa. [4]. Therefore, if A wants to send B a secure email, A should encrypt it using B's public key so that B may decrypt it using his own private key after receiving the encrypted email. When we state that A encrypts the report, all A actually does is run the file through a hashing programme. For any report, the hash function software programme generates a hard and fast duration of alphabets, numbers, and logos. The result of the hash algorithm is this. The hash result for two distinct documents is never the same. Any tiny change made to the file will produce a completely unique hash result. The hash result of a specific message will always be the same thanks to the hash function software. Therefore, all that has to be done to determine whether or not the message was intercepted is to look at the hash functions at both ends. The hash function, which encloses and transforms the initial digital record into any other digital document, and uneven cryptography (which is nothing but the public key cryptography system described above) will be used to authenticate the digital record. In essence, a digital signature certificate contains the owner's public key along with other information, such as contact information, and its most important element: the digital signature of the Certifying Authority [2].[7]. One of these certificates is primarily used to demonstrate that the statistics it contains have been attested by a reliable authority that has been appointed and managed by the government.

II. BENEFITS

1. While many business leaders and executives are interested in digital signatures, what precisely are they? A digital signature can be thought of as your electronic fingerprint.
2. It authenticates the signer and enables electronic signatures.
3. It is a mathematical code that verifies the sender of the document and guarantees that it reaches the recipient intact.
4. Digital signatures use a widely known format called a Public Key Infrastructure, which provides a very high level of security and makes it difficult to reproduce, thus concerns about its security are reasonable.
5. Office paperwork is much more efficient with digital signatures, however national restrictions on this technology differ.
6. Due to the advantages of digital signatures, more businesses and offices are adopting esignatures, creating a digitally safe and efficient workplace

III. LITERATURE REVIEW

The RSA algorithm, introduced by Rivest, Shamir, and Adleman in 1978, remains one of the most widely used digital signature algorithms. It is based on the computational difficulty of factoring large composite numbers (Rivest et al., 2021). The security of RSA relies on the difficulty of factorizing the modulus N, making it resistant to attacks based on prime factorization. Researchers have extensively studied RSA-based digital signature algorithms and their security properties. In a comprehensive analysis by Bellare and Rogaway (2022), they presented a provably secure digital signature scheme based on RSA. Their work established a theoretical foundation for RSA signatures, addressing security concerns such as unforgeability and resistance against chosen message.

Due to its robust security features and effective computing, elliptic curve-based digital signature algorithms, including the Elliptic Curve Digital Signature Algorithm (ECDSA), have attracted a lot of attention. Elliptic curve-based techniques provide shorter key lengths and quicker computations than RSA while preserving a comparable level of security. The security and efficiency of elliptic curve-based digital signature algorithms have been studied in several publications. Johnson et al. (2021) looked at the security of ECDSA and offered suggestions for parameter selection to guarantee a high enough level of security. They emphasised the significance of selecting suitable elliptic curve parameters and key sizes in order to fend off known assaults.

Researchers have focused on post-quantum cryptography (PQC) methods that provide resistance against attacks by quantum computers since the development of quantum computing. In a post-quantum age where traditional cryptographic methods, such as RSA and elliptic curve-based algorithms, may become vulnerable, PQC digital signature algorithms seek to guarantee security.

For post-quantum secure digital signatures, lattice-based digital signature algorithms have shown promise. The effectiveness and security of lattice-based signature methods have been studied. A provably secure lattice- based signature system was put out by Peikert and Waters (2008), who also emphasised the benefits of lattice-based cryptography in terms of security from both classical and quantum attackers.

Different digital signature algorithms have been compared based on their performance, security, and appropriateness for a range of applications. For instance, Li et al. (2018) compared the computational effectiveness and security characteristics of the RSA, ECDSA, and lattice-based digital signature algorithms. Their investigation provided insights into the actual use of each algorithm category by highlighting the benefits and trade- offs of each.

In conclusion, the reviewed literature demonstrates extensive research on digital signature algorithms, including RSA-based, elliptic curve-based, and post- quantum cryptographic algorithms. The studies have addressed various aspects such as security properties, performance analysis, parameter selection, and comparative evaluations. These research findings form the basis for a comprehensive review of digital signature algorithms, providing insights into their security and applications for practitioners and researchers in the field of cryptography.

IV. DIGITAL SIGNATURE

Digital signatures are cryptographic mechanisms used to ensure the authenticity, integrity, and non-repudiation of electronic documents, messages, or transactions in the digital realm. They work as the digital equivalent of handwritten signatures in conventional paper-based transactions, offering a safe mechanism to confirm the signer's identity and spot any changes to the data they have signed. By fostering trust and confidence in electronic communications, digital signatures make it possible for data to be sent securely and reliably through digital channels.

Digital signatures serve several purposes. They are used to verify the source of digital data in the first place. By using a digital signature, the signer links their distinct identity to the information they are signing, creating a way to confirm their identification. This assures that the data's source can be trusted and verifies that it was not altered during transmission. Second, digital signatures guarantee the accuracy of the data they sign. The recipient will be able to recognise and reject tampered data if any modifications or revisions are made to the signed content after the signature has been applied. Last but not least, digital signatures offer non-repudiation, which means that the signer cannot subsequently refute their participation in signing the letter or message. For contractual and legal reasons, the recipient can depend on the digital signature as proof of the signer's dedication to the content and intent. In general, electronic transactions and communications benefit from digital signatures' increased security and dependability.

A. Components of a Digital Signature Include

To guarantee the consistency, veracity, and non- repudiation of electronic documents or messages, a digital signature is made up of several crucial elements. These elements consist of: Private Key: The signer securely maintains the private  key, which is a special and private cryptographic key. To protect the integrity of the signing procedure, it must be kept a secret because it is utilised to create the digital signature.

V. RSA ALGORITHM

A. Overview of the RSA Algorithm

One of the most well-known and extensively studied public-key encryption and digital signature methods is the RSA (Rivest-Shamir-Adleman) algorithm. Leonard Adleman, Adi Shamir, and Ron Rivest first presented it in 1977. The computational challenge of factoring huge composite numbers into their prime factors forms the basis of the procedure.

The creation of a public-private key pair is a requirement of the RSA algorithm. While the private key is kept private and is used for decryption and signature creation, the public key is used for encryption and signature verification. Choosing two huge prime numbers, determining their product (n) as the modulus, and determining the totient ((n)) of the modulus are all steps in the key generation process. The public key is made up of the modulus (n), which is often a tiny prime value, and the public exponent (e). The private exponent (d), which is part of the private key, is obtained by modular arithmetic from the public key parameters. [3]

B. The RSA Signature Scheme

Public-key cryptography's fundamental ideas form the foundation of the RSA signature algorithm. The signer follows a set process to produce an RSA digital signature. To create a fixed-length digest, the message is first subjected to a hash function. After padding, the digest is converted into a numerical representation. The signature value is produced by the signer by exponentiating the padded digest using the private key. The recipient receives the message with the signature included.[4] The recipient of the signed communication can use the corresponding RSA public key to confirm the signature's legitimacy after receiving it. The signature is exponentiated by the recipient using the public key, which results in a number that represents the original digest. Using the same hash algorithm, the recipient also determines the message's digest. The signature is regarded as legitimate if the calculated digest agrees with the decrypted value.

C. Security Weaknesses and Possibilities

Digital signature methods based on RSA have a number of security advantages. Large composite numbers are computationally difficult to factor, which is the foundation of the security of RSA. Given sufficiently high key sizes, it is currently thought to be computationally impossible to break RSA, which requires security against conventional assaults.

However, there are some restrictions and potential weaknesses with RSA that must be taken into account. The choice of key sizes is crucial to RSA's security. To maintain the necessary level of security, higher key sizes are needed as processing power and factoring algorithms increase. Furthermore, RSA signatures do not naturally defend against selected ciphertext or malleability attacks. To prevent these issues, appropriate padding techniques like RSA-PSS or PKCS#1 v1.5 must be used.[5]

D. Performance Evaluation

The effectiveness of digital signature algorithms based on RSA is influenced by a number of variables, including as the size of the message, the size of the key, and the effectiveness of the modular exponentiation process. Modular exponentiation with the private key is a step in the RSA signature creation process that can be computationally demanding, especially for keys of greater sizes. On the other hand, modular exponentiation with the public key is used for signature verification, which is often quicker.

Performance of RSA methods is directly impacted by key size. Larger key sizes increase processing times and storage needs by requiring more computational power. Key creation and administration may need additional time and resources.[6]

E. Real-World Applications

In many different real-world situations where secure authentication and integrity verification are essential, RSA-based digital signature methods find extensive application. Examples of typical applications include: Secure Communication Protocols: To enable secure communication over the internet, protocols like Secure Sockets Layer/Transport Layer Security (SSL/TLS) use RSA. It facilitates safe key exchange and guarantees the validity of server certificates. Digital certificates: For safe identification and authentication, digital certificates use RSA signatures. To validate the legitimacy of people, companies, or websites, certificate authority issue certificates with RSA signatures.

RSA signatures are used in secure email systems to guarantee the authenticity and non-repudiation of email messages. They give the recipient the ability to confirm that the communication came from the stated sender and wasn't tampered with in route.

Digital document signing uses RSA signatures to ensure the authenticity and integrity of the document. This is crucial in situations involving law and business, because signed documents must have legal force.

Code signing: To sign software code and guarantee its integrity and authenticity, RSA signatures are utilised. Users can confirm that the software is authentic and has not been tampered with by using code signing certificates with RSA signatures.

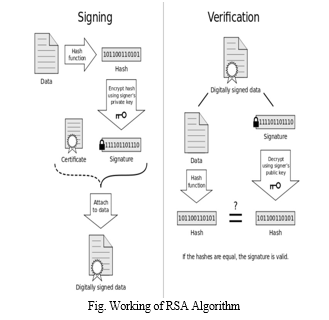
In conclusion, RSA-based digital signature algorithms are popular and offer high security in a range of practical applications. They are utilised for secure email systems, document signing, code signing, digital certificates, and secure communication protocols. Despite significant restrictions and potential weaknesses, RSA is still a popular option because of its well-proven security features and broad support across numerous platforms and applications.

VI. ELLIPTIC CURVE-BASED DIGITAL SIGNATURE ALGORITHMS

A subset of public-key cryptography called elliptic curve cryptography (ECC) is based on the algebraic characteristics of elliptic curves over finite fields. Despite using smaller key sizes than more established cryptographic methods like RSA, ECC offers security and performance advantages.

An elliptic curve is described by the equation y2 = x3 + axe + b in the ECC, where a and b are curve-specific constants. There are locations on the curve, including a unique point at infinity, that satisfy this equation. Point addition is the definition of the group operation on the curve, and it demonstrates closure, associativity, and the presence of an identity element. [6]

A. ECDSA, for example, is an ECC-based Signature scheme

The Elliptic Curve Digital Signature Algorithm (ECDSA) is one of the most used elliptic curve-based digital signature systems. In contrast to conventional methods like RSA, ECDSA offers good security with reduced key sizes and is based on the concepts of public-key cryptography.[6][7] The signer follows a precise technique to produce an ECDSA digital signature. To create a fixed-length digest, the message is first subjected to a hash function. Then the ephemeral private key, a random number, is chosen. By dividing the curve's base point by the temporary private key, the signer calculates a point on the elliptic curve. The generated point's x-coordinate is used as a temporary value. The signer then multiplies the digest with their private key and computes the modular inverse of the ephemeral private key. The signature is created by combining the values obtained, and it has two parts: the r-value and the s-value. The recipient receives the message with the signature included.

The recipient of the signed communication can use the matching ECDSA public key to confirm the signature's legitimacy after receiving it. The recipient runs a series of calculations using the original message digest, the received signature, and the recipient's public key. The signature is regarded as valid if the calculations result in the anticipated values.[7]

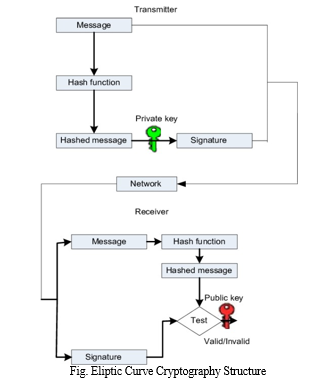
B. Security Weaknesses and Possibilities

Digital signature techniques based on elliptic curves, like ECDSA, have various security advantages. The elliptic curve discrete logarithm issue, which is thought to be computationally challenging to solve, is the foundation for the security of ECC. Compared to other conventional algorithms, ECC offers comparable security with smaller key sizes. Because of the smaller key sizes, ECC is more advantageous in contexts with limited resources in terms of computing and storage needs.[6]

ECC does, however, have several restrictions and potential weaknesses, just like any other cryptographic technique. The correct choice of elliptic curve parameters is crucial for maintaining ECC's security. The security of ECC may be jeopardised if a weak curve or bad parameter selections are used. The implementation of ECC-based systems may also be vulnerable to implementation mistakes or side-channel attacks. Therefore, while utilising ECC-based digital signature algorithms, it is imperative to adhere to suggested rules and best practises.[7]

C. Performance Evaluation

Algorithms for digital signatures that are based on elliptic curves have advantages in performance. Modern computing systems may effectively implement the computations required for ECC, such as point multiplication on elliptic curves. Compared to conventional techniques like RSA, this results in computations that are faster. ECC's smaller key sizes further lower the amount of space needed to store both keys and signatures.

The effectiveness of ECC-based signature schemes is impacted by a number of variables, including the key size, message size, and the effectiveness of point multiplication operations. ECC's performance can be slightly impacted by larger key sizes, but this effect is often less severe than it is for RSA. ECC is especially well suited for contexts with limited resources or applications that demand effective functioning and minimal bandwidth utilisation.

D. Applications in the Real World

Elliptic curve-based digital signature algorithms are used in a variety of real-world contexts where efficiency and security are paramount. Examples of typical applications include:

1. Safe Communication Protocols: To provide safe communication over networks, secure communication protocols like TLS (Transport Layer Security) and SSH (Secure Shell) use ECC-based algorithms, including ECDSA. They guarantee the privacy, accuracy, and legitimacy of the information sent between endpoints.
2. Secure IoT Networks: ECC is an excellent choice for safeguarding Internet of Things (IoT) networks that contain resource-restricted devices with confined memory and processing capability. ECC-based digital signatures are excellent for safeguarding IoT devices and guaranteeing the integrity and authenticity of data transported within IoT networks because they offer strong security with lower key sizes.
3. Secure Messaging and Email Systems: To guarantee authentication and non-repudiation, secure messaging and email systems use ECC-based signatures. They ensure that the communications haven't been altered with while in transit and confirm the sender's identity.
4. Mobile Device Security: For secure communication and digital signatures, ECC is frequently employed in mobile devices like smartphones. It is ideal for safeguarding mobile applications and transactions because of its effectiveness and reduced key sizes.
5. Blockchain Technology: To authenticate transactions, guarantee data integrity, and prove ownership, blockchain technology makes extensive use of ECC- based digital signatures. Due to its effectiveness and robust security features, ECC is a good fit for blockchain networks that demand quick and secure transaction verification.

In conclusion, elliptic curve-based digital signature algorithms, like ECDSA, offer significant benefits in terms of efficiency and security. Applications for ECC can be found in blockchain technology, secure IoT networks, secure messaging and email systems, and mobile device security. It is a well-liked option for situations where there are few resources or when efficient operations are essential because of its lower key sizes, faster computations, and reduced storage needs. The security of ECC-based digital signature schemes depends on proper parameter selection and implementation techniques.

VII. POST-QUANTUM CRYPTOGRAPHIC (PQC) ALGORITHMS

A. Traditional Algorithms Face Quantum Threats

Traditional cryptographic algorithms, particularly those used for digital signatures, are seriously threatened by the development of quantum computers. By taking advantage of the underlying mathematical assumptions of popular algorithms like RSA and elliptic curve-based cryptography, quantum computers have the ability to crack them. The security for these techniques is based on the efficient solution of two problems, the integer factorization problem and the discrete logarithm problem on elliptic curves.

The security of digital signatures based on these conventional algorithms may be compromised by the development of powerful, fault-tolerant quantum computers. Post-quantum cryptography (PQC) techniques are thus required in order to fend off assaults from both classical and quantum computers.[8]

B. PQC Algorithm Overview

In a world where quantum computers can effectively answer specific mathematical problems, post-quantum cryptography techniques seek to offer security. To defend against attacks from both classical and quantum computers, these algorithms investigate various mathematical constructions and computational premises.

Lattice-based, code-based, multivariate, hash-based, and isogeny-based algorithms are only a few examples of the many families of PQC algorithms. These algorithms are built on various mathematical structures or issues that are thought to be challenging for both conventional and quantum computers to solve. Analysis of PQC algorithms' efficiency, effectiveness, and applicability for real-world use are all part of their study and development.[8][9]

C. Signatures using a Lattice

The security offered by lattice-based digital signature algorithms takes use of the difficulty of specific lattice problems. In multidimensional space, lattices are geometrical objects that can be visualised as grids or collections of points. Based on the difficulty of lattice problems like the Shortest Vector challenge (SVP) or the Learning With Errors (LWE) challenge, lattice-based signatures are created.[10] Strong defence against both conventional and quantum attacks is provided by lattice-based signatures. They can withstand attacks utilising Shor's algorithm, a quantum technique that is effective at addressing some issues. On the basis of well-researched mathematical puzzles, lattice-based signatures offer demonstrable security guarantees.[9]

D. Code-Based Signatures

The security of code-based digital signature methods depends on the toughness of specific error-correcting codes. These algorithms' foundations are error-correcting codes, which can effectively fix mistakes in a message after it has been received. The incapability of decoding a symptom to access the private key underpins the security of code-based signatures.

Coding-based signatures benefit from established cryptographic security. The complexity of a syndrome's decoding is based on well-researched mathematical conundrums. Since there is no known quantum algorithm that can effectively address the decoding challenge, code-based signatures are immune to attacks utilising quantum computers.

E. Multivariate Cryptography

Another class of PQC algorithms that provide security based on the difficulty of resolving systems of multivariate polynomial equations is known as multivariate cryptography. Sets of multivariate polynomials are used to create multivariate cryptographic signatures, and the security of these signatures depends on how difficult it is to solve the underlying equations.

Multivariate signatures provide defence against both conventional and unconventional threats. However, the security of these systems depends on the polynomial systems chosen and how challenging they are to solve. The overall security of multivariate cryptographic methods must be ensured by careful selection and study of the polynomial systems.

F. Security Weaknesses and Possibilities

Digital signature methods for post-quantum cryptography offer a number of security benefits. Long- term security is guaranteed even in the presence of potent quantum computers thanks to their resistance to attacks from both classical and quantum computers.

PQC algorithms' security is built on a variety of challenging mathematical problems or structures that are thought to be impossible for quantum algorithms to solve effectively. PQC algorithms do, however, have constraints and potential weaknesses. PQC algorithms require in-depth investigation, evaluation, and standardisation to prove their security features and thwart potential attacks because they are relatively new cryptographic algorithms. In comparison to conventional algorithms, some PQC algorithms may have bigger key sizes, greater computational complexity, or longer processing times. Furthermore, adequate implementation and adherence to suggested best practises are necessary for the real-world security of PQC algorithms.[9]

G. Performance Evaluation

Post-quantum cryptographic digital signature methods' performance is influenced by a number of variables, including the particular algorithm, key size, implementation effectiveness, and hardware capabilities. Different PQC algorithms might have various performance traits. Some lattice-based signature methods enable effective operations with more manageable key sizes, making them somewhat practical. Code-based signatures can also be effective, but bigger key sizes might be needed. In comparison to conventional algorithms, multivariate cryptographic signatures may have a higher computing cost, larger key sizes, or longer processing times. It is significant to highlight that research and optimisation efforts are continually focused on improving the performance of PQC algorithms. Ongoing work aims to raise their effectiveness, shrink essential sizes, and enhance their performance for real-world uses.[10]

H. Applications in the Real World

Algorithms for post-quantum cryptographic digital signatures could be applied in a range of real-world scenarios where long-term security is crucial. These algorithms have not yet been widely adopted in the actual world because they are still being created and standardised. However, a few possible uses include:

1. Secure Communication Protocols: To guarantee the confidentiality, integrity, and authenticity of data sent via networks, secure communication protocols can use PQC algorithms.
2. Secure Cloud Computing: PQC techniques can be used in cloud computing environments to secure data storage, retrieval, and processing, shielding critical data from potential quantum attacks.
3. Financial Systems: In banking and payment systems, PQC algorithms can be used to safeguard financial transactions and guarantee the integrity and authenticity of digital signatures.
4. Government Communications: PQC algorithms can offer safe channels for transmitting private information to and from the government, guarding against potential assaults from both classical and quantum computers.
5. Critical Infrastructure Protection: Where long-term security is crucial, PQC algorithms can be used to secure critical infrastructure systems, such as power grids, transportation networks, and healthcare systems.

Their usefulness and applicability for various real-world settings will be better understood and validated as PQC algorithms become more widely used and standardised.

In conclusion, post-quantum cryptographic digital signature techniques provide long-term security from both classical and quantum threats. Among the families of PQC algorithms being researched and tested are multivariate, lattice-based, and code-based cryptographic algorithms. These algorithms have a variety of security advantages, but they also have drawbacks and might affect performance. Their practical uses and performance characteristics will become better understood as research and standardisation efforts proceed, enabling their implementation in crucial systems needing quantum-resistant security.[10]

VIII. COMPARISON AND EVALUATION

A. Trade-offs and Security Considerations

The security aspects and trade-offs of various digital signature algorithms have been widely explored, and RSA-based methods have a long history of use. When properly sized keys are used, they provide robust security by depending on the computationally challenging nature of factoring huge composite numbers. But RSA's security depends on the notion that factoring big numbers is computationally impossible.

Larger key sizes are required with RSA in order to ensure security against factoring algorithms and increasingly potent computer resources. Performance, key management, and key storage may all be impacted by this trade-off.

Digital signature techniques based on elliptic curves, like ECDSA, offer an alternate strategy. They are more effective in terms of computational resources, key storage, and bandwidth since they provide security that is comparable to RSA but with substantially smaller key sizes. Based on how challenging the discrete logarithm problem for elliptic curves is, elliptic curve methods are secure. To ensure their security, the elliptic curves and parameters chosen are essential. Elliptic curve algorithms must also take into account any potential weaknesses, such as side-channel attacks or flaws in certain curve selections.

Methods for post-quantum cryptographic digital signatures are being developed in response to the threat posed by quantum computers, which have the ability to crack elliptic curve-based and traditional cryptographic methods like RSA. Lattice-based, code-based, and multivariate cryptography are a few examples of these algorithms that offer defence against quantum attacks. They do, however, have their own disadvantages. Code- based signatures rely on error-correcting codes, whereas multivariate cryptography takes advantage of the difficulty of solving multivariate polynomial equations. Lattice-based signatures take advantage of the hardness of some lattice problems. These post-quantum cryptography algorithms frequently call for higher key sizes, more difficult computations, or longer processing times, which may affect their usability and efficiency.

B. Performance Measurements

When it comes to speed, RSA-based digital signature algorithms verify signatures more quickly than they can generate them. A modular exponentiation operation is used in the efficient signature verification process.

However, it can be computationally expensive to generate signatures because it necessitates modular exponentiation using the private key, especially for bigger key sizes. The key size has a direct bearing on the computational difficulty of RSA, with longer keys requiring greater computing power. Additionally, there may be additional time and storage requirements associated with the creation and management of RSA keys.

Algorithms for digital signatures that are based on elliptic curves have advantages in performance. On current computing platforms, point multiplication on elliptic curves can be implemented effectively for both signature creation and verification procedures. Even with reduced key sizes, this results in computations that are faster.

Elliptic curve-based algorithms are more suited for contexts with limited resources, like embedded systems or mobile devices, because the smaller key sizes also lead to decreased storage needs and shorter signature lengths. The choice of elliptic curve parameters, effective implementation strategies, and the complexity of the underlying processes, however, can all affect how well elliptic curve algorithms perform.

The performance characteristics of post-quantum cryptography digital signature methods differ. For instance, lattice-based signatures are comparatively practical because they provide effective operations with reduced key sizes. Code-based and multivariate cryptography, on the other hand, could have higher computational costs, bigger key sizes, or longer processing times. When analysing the effectiveness of post-quantum cryptography algorithms for specific use cases, these aspects must be properly taken into account.[13]

C. Adaptability to Various Use Cases

Digital signature algorithms' usefulness for diverse use cases is influenced by a number of variables, including the required security level, performance requirements, and application context. Digital signature techniques based on RSA have a long history and are often used in many applications. They are appropriate in situations when the speed of key creation and verification is not crucial and the resilience of a tried-and-true technique is sought. In applications where security is crucial, such as secure email systems, digital certificates, and secure communication protocols, RSA is frequently utilised.[11]

Elliptic curve-based digital signature algorithms are suited for resource-constrained situations or applications that demand efficient operations because they provide robust security with reduced key sizes and faster computations. They are frequently employed in secure messaging apps, secure IoT networks, secure communication protocols, and other contexts where computational effectiveness is an important factor.

Digital signature methods for post-quantum cryptography are currently in the research and development stage. The particular algorithm's security and performance properties determine if they are suitable. The use of post-quantum cryptographic algorithms may be required in situations where long- term security and resilience to quantum attacks are essential, such as secure government communications or critical infrastructure protection.

When determining whether bigger key sizes are appropriate for a given use case, it is important to carefully weigh the trade-offs, potential performance effects, and current standardisation initiatives.[12][14]

In conclusion, choosing the best digital signature algorithm for a particular application necessitates carefully weighing the security aspects, performance metrics, and appropriateness of several algorithms.[12] RSA-based techniques provide well-known security but could necessitate bigger key sizes. With lower key sizes and quicker computations, elliptic curve-based algorithms offer comparable security. In order to combat the threat posed by quantum computers, post- quantum cryptography algorithms must be assessed for their security, performance, and standardisation status. In order to guarantee the appropriate security level and performance for the specified use case, the selection of a digital signature algorithm should be based on a thorough evaluation of these aspects.

IX. RECENT DEVELOPMENTS AND FUTURE DIRECTIONS IN DIGITAL SIGNATURES ALGORITHMS

A. Quantum-safe Cryptography

The growing danger posed by quantum computers has greatly affected recent improvements in digital signature algorithms. There is a need for quantum-safe or post-quantum cryptographic algorithms since quantum computers have the ability to crack conventional cryptographic methods, such as RSA and elliptic curve- based algorithms. In order to protect users from attacks from both classical and quantum computers, quantum- safe cryptography was developed.[13]

Lattice-based, code-based, multivariate, hash-based, and isogeny-based algorithms are only a few of the methods being investigated for quantum-safe cryptography. These algorithms are claimed to be resistant to attacks by both classical and quantum computers since they are based on several mathematical foundations and computational assumptions. The current work in quantum-safe cryptography focuses on finding algorithms with good security characteristics, examining their weaknesses, and enhancing their performance for real-world use.[12][9]

B. Efforts at Standardisation

The acceptance and use of digital signature algorithms depends heavily on standardisation. In order to facilitate secure and effective cryptographic implementations, standardisation efforts strive to offer rules, specifications, and compatibility. Standardisation efforts in the context of digital signatures are mostly concentrated on secure cryptographic protocols and post-quantum cryptographic techniques.

Several organisations, including the National Institute of Standards and Technology (NIST) and the European Telecommunications Standards Institute (ETSI), are driving standardisation attempts for post-quantum cryptography algorithms. These programmes feature open contests and teamwork among specialists from around the world to assess and choose the most promising post-quantum cryptographic algorithms. To make sure that the chosen algorithms are secure, effective, and interoperable, the standardisation process entails rigorous analysis, testing, and examination.[16]

Standardisation efforts cover strong cryptographic techniques for digital signatures in addition to post- quantum cryptography. For instance, organisations that develop and maintain standards for secure communication protocols like TLS (Transport Layer Security) and the Cryptographic Message Syntax (CMS) include the Internet Engineering Task Force (IETF) and the International Organisation for Standardisation (ISO). certain standards specify how digital signatures should be used inside certain protocols, assuring security and interoperability across various implementations.[14]

C. Emerging Digital Signature Algorithms

Emerging digital signature algorithms have made major strides in recent years, aiming to address the changing security landscape and satisfy the needs of contemporary cryptographic applications. These algorithms provide greater efficiency, increased security, and flexibility to new cryptographic problems. These prominent new digital signature algorithms are listed below:

Boneh-Lynn-Shacham, sometimes known as BLS, is a pairing-based digital signature method that has drawn attention for its effectiveness and robust security features. Compared to conventional techniques like RSA and ECDSA, it offers shorter signatures and quicker verification. In applications like blockchain technology, where efficiency and compactness are essential, BLS signatures are very helpful. BLS signatures have been incorporated into a number of blockchain platforms and are being thought of for a number of different uses.[17]

A hash-based digital signature system that offers defence against both conventional and quantum assaults is called XMSS (Extended Merkle Signature Scheme). It provides high security guarantees and is based on the idea of Merkle trees. Since XMSS is intended to be stateful, managing private keys is necessary, and keys cannot be reused. In their post-quantum cryptography competition, NIST standardised XMSS, which is seen as a promising post-quantum cryptographic method for digital signatures.[18]

SPHINCS (SPHINCS+): The SPHINCS family of stateless hash-based signature methods provides protection from both conventional and quantum assaults. To create signatures, SPHINCS uses a tree- based structure and hash algorithms. While offering robust security guarantees, it is also resistant to numerous threats. The SPHINCS+ scheme fixes some of the shortcomings of the original SPHINCS design. It provides more effectiveness and is being taken into consideration for post-quantum secure applications.[19]

Ring Learning with Errors, or R-LWE The R-LWE lattice-based digital signature algorithm depends on the difficulty of lattice-related problem solving. It is a strong contender for post-quantum cryptography since it provides strong security against both conventional and quantum assaults. The Ring Learning with Errors problem, which entails resolving systems of polynomial equations, is the foundation for R-LWE signatures. As part of the continuing standardisation work for post- quantum cryptography, R-LWE is now being researched and standardised.[20]

These new digital signature algorithms continue to be thoroughly studied, assessed, and standardised. They provide promising answers to the problems brought on by the introduction of quantum computers and the changing cryptography environment. These algorithms' performance is being optimised, and researchers are striving to make sure they are appropriate for a variety of practical applications. Emerging digital signature algorithms are being created in response to the demand for post-quantum security, increased efficiency, and improved security features.

These algorithms offer protection from quantum attacks and serve as substitutes for more established ones like RSA and elliptic curve-based algorithms. They aim to address the shortcomings of conventional algorithms and provide long-term security in the face of technological advancement.

The adoption and application of new digital signature algorithms depends heavily on standardisation initiatives. The standardisation initiatives to assess, choose, and establish rules for the application of these algorithms are being led by organisations like NIST and ETSI. The objective is to guarantee efficiency, security, and interoperability across many implementations.[18]

Research, evaluation, and standardisation are still being done on these new digital signature algorithms. They provide resistance against quantum assaults and overcome the shortcomings of conventional algorithms, offering viable answers to the changing security landscape. Ongoing work aims to evaluate their performance, assure their applicability for diverse real- world applications, and analyse their security characteristics.

In conclusion, the need for quantum-safe cryptography and the advent of new cryptographic requirements have motivated recent breakthroughs in digital signature algorithms. Post-quantum cryptography is a rapidly developing topic as a result of ongoing research, efforts at standardisation, and the creation of novel algorithms. To assure security in a post-quantum future, quantum- safe cryptography methods are being investigated.

Guidelines and requirements for secure cryptographic implementations are provided by standardisation efforts. Digital signature algorithms that are currently being developed, like BLS, XMSS, SPHINCS, and R-LWE, promise improved security and effectiveness. These algorithms are anticipated to be extremely important as the industry develops in the future for maintaining the security and dependability of digital signatures.

X. DISCUSSION

A. Cryptographic hashing

Without using a key, a hash feature converts a message with a variable duration into one with a fixed duration hash cost or message digest. It is recognised as a cryptographic hash characteristic that is computationally impossible to find either a message that maps to a previously unique hash value or messages that map to the same hash value. This hash characteristic is desired for security applications. In other words, a cryptographic hash feature should possess both the one-way and the collision-resistant properties. The aforementioned residences are utilised to determine whether or not the related message has been altered using a cryptographic hash value. However, The hash value must be secured.

B. Electronic Signature

Using information specific to the signer and depending on the message being signed, a digital signature is a bit sample. A cryptographic hash function is used to generate a hash value or message digest from the input message M. Using the signer's private key, the hash fee h, which is dependent on the message M, is encrypted to produce the signature. The result hash value of the message M' is compared to the value obtained by decrypting the signature using the signer's public key in order to determine whether or not the digital signature is legitimate. The message's author is the owner of the public key if each value is the same. The signature is not valid if anything else. Three methods are included in the Digital Signature Standard (DSS): the Elliptic Curve Digital Signature Algorithm (ECDSA), the RSA digital signature algorithm, and the Digital Signature Algorithm (DSA).[22]

The cryptographic hash function and the public key cryptography set of rules are what keep a digital signature secure. An attacker can create a fake digital signature to circumvent a digital signature by adding a new message to an existing digital signature—a tactic known as a cryptographic hash feature—or by creating a fake virtual signature for a given message—a tactic known as a general public key cryptographic algorithm. The public key algorithm must be immune to assaults and the hash feature must be collision-resistant. The approved methods are regarded as secure. A digital signature cannot be faked due to computational limitations. Non-repudiation and authentication are provided via the digital signature. As a result, if the signature is authentic, the message's author cannot dispute creating it

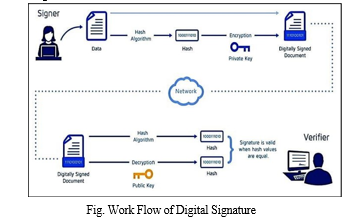
A. Authority for Certificates

Digital certificates are offered by Trust Service Providers (TSP), who make sure that documents are signed and keys are issued in a secure environment.[23]

B. Electronic ID

A digital representation of information about a person or entity that is based on ITU-T X.509 v3 standards. It is kept on a computer or in a group of computers, a USB token, a smart card, and many more places. A public key certificate, a private key, and additional information are included in a digital ID.

C. Certificates digital

Aid in establishing a certificate's holder's legitimacy. Digital certificates are digitally signed by a Certificate authority and contain the sender's public key.[24]

The public key infrastructure (PKI), which supports the distribution of public keys and the identification of users via virtual certificates and a certificates authority, consists of rules, protocols, regulations, people, and structures.[25]

D. Digital signatures are recognised as legal documents in several nations throughout the world.

1. The Uniform Electronic Transactions Act (UETA) 1999 and The E-sign Act 2000, USA
2. The European Union’s Electronic Signatures Directive, Directive 1999/93/EC
3. The Information Technology Act 2008, India
4. The Electronic Communications and Transactions Act 2002, South Africa
5. UNCITRAL Model Law on Electronic Signatures 2001

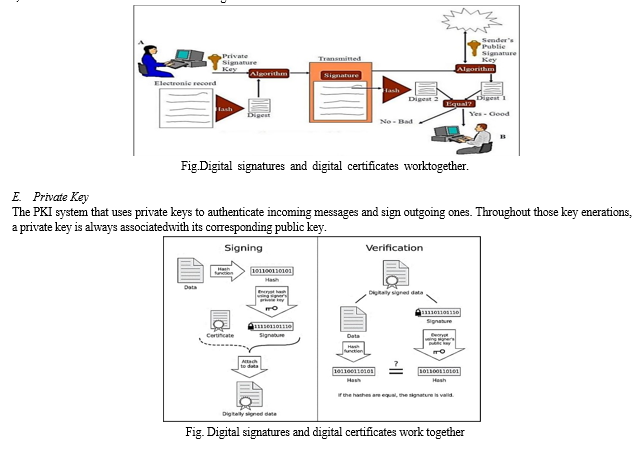
Conclusion

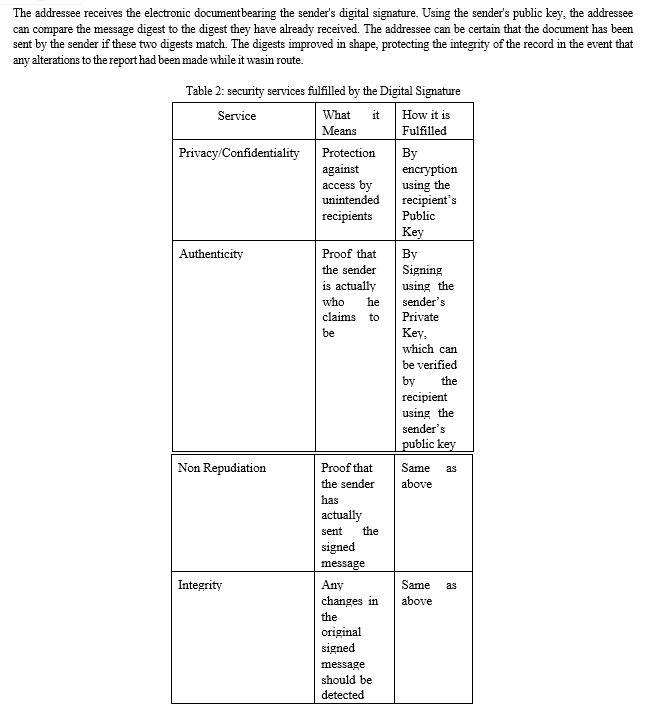
Key Takeaways: This review paper has offered a thorough overview of digital signature algorithms, including those based on RSA, elliptic curves, and post- quantum cryptography. This investigation reveals several important conclusions: 1) RSA-based digital signature algorithms have received a lot of attention and adoption, and they provide robust security with solid mathematical underpinnings. However, considering post-quantum cryptography options is necessary due to their susceptibility to quantum attacks.[3] 2) Digital signature algorithms based on elliptic curves, like ECDSA, offer effective operations, lower key sizes, and resilience to quantum assaults. They have applications in secure communication, IoT networks, and mobile device security and operate well in circumstances with limited resources. 3) Post-quantum cryptographic digital signature algorithms, which strive to fend off assaults from both classical and quantum computers, represent the future of safe digital signatures. Although they need more study, standardisation, and optimisation, lattice-based, code- based, and multivariate cryptographic algorithms are potential possibilities that provide resistance to quantum attacks.[8][9] A. Suggestions for Real-World Application Several suggestions for the effective implementation of various digital signature algorithms can be provided based on the evaluation of those algorithms: 1) When choosing digital signature algorithms, organisations should analyse their security needs and take quantum threats into account. For short-term security, RSA-based algorithms might still be appropriate, however switching to post-quantum cryptographic algorithms is advised for long-term security.[10] 2) Implementers must adhere to suggested rules and best practises for the particular digital signature algorithm they have selected. This includes choosing the right key size, choosing parameters wisely, managing keys securely, and adhering to suggested padding methods and protocols.[9] In order to establish the security characteristics, effectiveness, and interoperability of new post- quantum cryptographic algorithms, further research, evaluation, and standardisation initiatives are required. To ensure a smooth transition to quantum-safe cryptography, organisations should stay up to date on developments in the field and take part in standardisation projects.[13] Future Prospects: Post-quantum cryptographic algorithms that can offer security in the face of quantum computers are what will determine the future of digital signature algorithms. Lattice-based, code- based, and multivariate cryptography research and standardisation efforts should result in useful and effective solutions. Additionally, there are promising futures for the integration of digital signatures with cutting-edge technologies like blockchain, the Internet of Things (IoT), and secure cloud computing. The security, integrity, and authenticity of digital transactions, data transfers, and decentralised systems can all be improved with the help of digital signatures and associated technologies. Additionally, improvements in hardware technology, including the usage of specialised hardware accelerators and quantum-resistant hardware, can aid in the effective implementation of digital signature algorithms and make it easier for them to be used in practical applications.[23] The analysis of digital signature algorithms has demonstrated the value of taking into account the security, functionality, and potential of various algorithms.[5] When choosing and implementing digital signature algorithms, organisations and implementers should carefully assess their security needs, keep up with post-quantum cryptography developments, and make informed selections. Future secure and reliable digital communication is greatly enhanced by the move to quantum-safe cryptography and the incorporation of digital signatures with cutting-edge technologies.[6]The addressee receives the electronic document bearing the sender\'s digital signature. Using the sender\'s public key, the addressee can compare the message digest to the digest they have already received. The addressee can be certain that the document has been sent by the sender if these two digests match. The digests improved in shape, protecting the integrity of the record in the event that any alterations to the report had been made while it was in route.[12]

References

[1] Katz, J., & Lindell, Y. (2021). “Introduction to Modern Cryptography”. Chapman and Hall/CRC. [2] Schneier, B. (2020). “Applied Cryptography: Protocols, Algorithms, and Source Code in C”. Wiley. [3] U. R. Bodasingi and S. Gunupuru, “New Digital Signature Scheme Based on RSA Using Circulant Matrix,” SN Computer Science, vol. 4, no. 3, Mar. 2023, doi: 10.1007/s42979-023-01694-4. [4] M. M. Ahmed, “Digital Signature with RSA Public Key Cryptography for Data Integrity in SOSE-Based E- Government Systems,” International Journal of Management, Technology, and Social Sciences, pp. 59– 70, Jan. 2022, doi: 10.47992/ijmts.2581.6012.0177. [5] J. Chandrashekhara, A. V B, P. H, and R. B R, “A COMPREHENSIVE STUDY ON DIGITAL SIGNATURE,” International Journal of Innovative Research in Computer Science & Technology, vol. 9, no. 3, May 2021, doi: 10.21276/ijircst.2021.9.3.7. [6] L. Lawrence and S. R., “VECDSigL: Video integrity verification using elliptic curve digital signature links,” Software Impacts, vol. 15, p. 100474, Mar. 2023, doi: 10.1016/j.simpa.2023.100474. [7] R. Ma and L. Du, “Attribute-Based Blind Signature Scheme Based on Elliptic Curve Cryptography,” IEEE Access, vol. 10, pp. 34221–34227, 2022, doi: 10.1109/access.2022.3162231. [8] C. Balamurugan, K. Singh, G. Ganesan, and M. Rajarajan, “Post-Quantum and Code-Based Cryptography—Some Prospective Research Directions,” Cryptography, vol. 5, no. 4, p. 38, Dec. 2021, doi: 10.3390/cryptography5040038. [9] H. Nejatollahi, N. Dutt, S. Ray, F. Regazzoni, I. Banerjee, and R. Cammarota, “Post-Quantum Lattice- Based Cryptography Implementations,” ACM Computing Surveys, vol. 51, no. 6, pp. 1–41, Jan. 2019, doi: 10.1145/3292548. [10] V. Chamola, A. Jolfaei, V. Chanana, P. Parashari, and V. Hassija, “Information security in the post quantum era for 5G and beyond networks: Threats to existing cryptography, and post-quantum cryptography,” Computer Communications, vol. 176, pp. 99–118, Aug. 2021, doi: 10.1016/j.comcom.2021.05.019. [11] F. G. Tawfeeq and A. M. Abdul-Hadi, “Improved throughput of Elliptic Curve Digital Signature Algorithm (ECDSA) processor implementation over Koblitz curve k-163 on Field Programmable Gate Array (FPGA),” Baghdad Science Journal, vol. 17, no.3(Suppl.), p. 1029, Sep. 2020, doi: 10.21123/bsj.2020.17.3(suppl.).1029. [12] N. Q. Luc, T. T. Nguyen, D. H. Quach, T. T. Dao, and N. T. Pham, “Building Applications and Developing Digital Signature Devices based on the Falcon Post-Quantum Digital Signature Scheme,” Engineering, Technology & Applied Science Research, vol. 13, no. 2, pp. 10401–10406, Apr. 2023, doi: 10.48084/etasr.5674. [13] A. A. Moldovyan, “Post-quantum digital signature algorithm with doubled verification equation,” Information Security Questions, no. 2, pp. 54–60, 2023, doi: 10.52190/2073-2600_2023_2_54. [14] L. Lawrence and S. R., “VECDSigL: Video integrity verification using elliptic curve digital signature links,” Software Impacts, vol. 15, p. 100474, Mar. 2023, doi: 10.1016/j.simpa.2023.100474. [15] S.-G. Liu, W.-Q. Chen, and J.-L. Liu, “An Efficient Double Parameter Elliptic Curve Digital Signature Algorithm for Blockchain,” IEEE Access, vol. 9, pp.77058–77066, 2021, doi:10.1109/access.2021.3082704. [16] I. Dinur and G. Leurent, “Preface to Volume 2020, Special Issue on Designs for the NIST Lightweight Standardisation Process,” IACR Transactions on Symmetric Cryptology, pp. 1–4, Jun. 2020, doi: 10.46586/tosc.v2020.is1.1-4. [17] N.-Q. Luc, Q.-T. Do, and M.-H. Le, “Implementation of Boneh - Lynn - Shacham short digital signature scheme using Weil bilinear pairing based on supersingular elliptic curves,” Ministry of Science and Technology, Vietnam, vol. 64, no. 12, pp. 3–9, Dec.2022, doi: 10.31276/vjste.64(4).03-09. [18] L. Li, X. Lu, and K. Wang, “Hash-based signature revisited,” Cybersecurity, vol. 5, no. 1, Jul. 2022, doi: 10.1186/s42400-022-00117-w. [19] S. Sun, R. Zhang, and H. Ma, “Efficient Parallelism of Post-Quantum Signature Scheme SPHINCS,” IEEE Transactions on Parallel and Distributed Systems, vol. 31, no. 11, pp. 2542–2555, Nov. 2020, doi: 10.1109/tpds.2020.2995562. [20] S. Kumar, G. Mittal, and S. Kumar, “Digital Signature Schemes Based on Group Ring,” SN Computer Science, vol. 3, no. 5, Jul. 2022, doi: 10.1007/s42979-022-01286-8. [21] M. Ouyang, Z. Wang, and F. Li, “Digital signature with cryptographic reverse firewalls,” Journal of Systems Architecture, vol. 116, p. 102029, Jun. 2021, doi: 10.1016/j.sysarc.2021.102029 [22] R. C. Ribeiro, M. G. de Almeida, and E. D. Canedo, “A Digital Signature Model Using XAdES Standard as a Rest Service,” Information, vol. 12, no. 8, p. 289, Jul. 2021, doi: 10.3390/info12080289. [23] Y. N. Wei, Y. T. Jin, and J. W. Zhou, “Design and Realization of RSA Digital Signature System Based on Digital Certificate,” Applied Mechanics and Materials, vol. 743, pp. 698–701, Mar. 2015, doi: 10.4028/www.scientific.net/amm.743.698. [24] D. T. Nguyen, “CONSTRUCTING DIGITAL SIGNATURE ALGORITHMS BASED ON NEW KEY SCHEMES,” Journal of Science and Technique, vol. 9, no. 2, Mar. 2021, doi: 10.56651/lqdtu.jst.v9.n02.207.ict. [25] G. B and S. M, “An Improved Public Key Infrastructure (PKI)-Based Digital Signature Authentication Service for Higher Key Storage System,” BOHR International Journal of Smart Computing and Information Technology, vol. 3, no. 1, pp. 1–6, 2020, doi: 10.54646/bijscit-19

Copyright

Copyright © 2024 Deepanshu Rana. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.