Applications of Algebra in Topological Data Analysis: Bridging Algebra and Data Science

Abstract

Topological Data Analysis (TDA) has emerged as a powerful framework for understanding the shape and structure of data. Algebra, particularly concepts from homological and computational algebra, plays a pivotal role in TDA by enabling the extraction of robust topological features from complex datasets. This review explores the applications of algebra in TDA, highlighting its contributions to data science. We discuss foundational concepts, methodologies, computational tools, and practical applications, providing insights into the intersection of algebra and data-driven insights. We delve into the theoretical foundations of TDA, highlighting the construction of simplicial complexes, the computation of homology and persistent homology, and the development of efficient algorithms for large-scale data analysis. Furthermore, we examine the integration of TDA with machine learning, its applications across various domains including image and signal processing, natural language processing, and biosciences and discuss current challenges and future directions in the field. By bridging the gap between abstract algebraic theories and real-world data analysis, this paper underscores the transformative potential of TDA in advancing data science methodologies.

Introduction

I. INTRODUCTION

In an era of data deluge, extracting meaningful insights from complex, high-dimensional datasets is a significant challenge. TDA offers tools to analyze the "shape" of data, capturing geometric and topological patterns that traditional statistical methods often miss. Algebra, particularly through concepts such as groups, rings, modules, and vector spaces, provides the theoretical foundation for many of TDA’s core techniques. This paper reviews how algebra facilitates TDA, emphasizing its applications in data science.[1]

The interplay between algebra and topology in TDA allows researchers to study the intrinsic structure of datasets without requiring explicit geometric embeddings. For instance, persistent homology—a cornerstone of TDA—relies on algebraic structures to quantify and track topological features such as connected components, holes, and voids across multiple scales. These insights have found applications in diverse fields, from computational biology and machine learning to sensor networks and financial modeling.[2] This paper aims to provide a comprehensive review of the role of algebra in TDA, discussing its theoretical underpinnings, computational methodologies, and practical applications. We also highlight challenges and future directions to inspire further research at this interdisciplinary intersection. Toillustrate how topology can be helpful, consider some examples of 2-dimensional point clouds in Figure 1 below. [3,4]

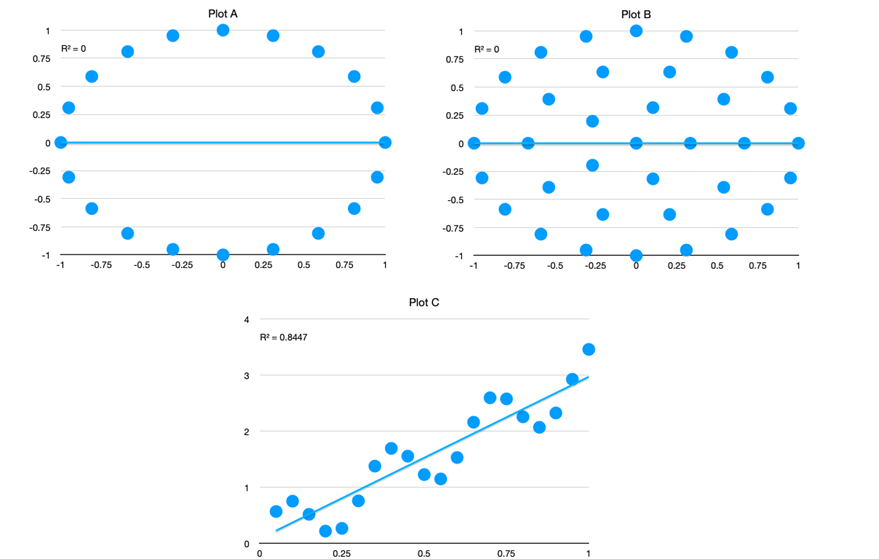
Figure 1. Scatterplots A, B, and C with R2 values of 0, 0, and 0.8447, respectivel

II. BACKGROUND/THEORETICAL FOUNDATIONS

This section offers essential background information, introducing fundamental concepts and theories related to algebra and topological data analysis. It sets the stage for readers to understand the subsequent discussions.[5]

A. Linear Algebra Tools for Data Analysis

Linear algebra serves as the cornerstone for many data analysis techniques, including those in TDA. Key concepts to cover include:

1. Vector Spaces and Linear Transformations: Understanding vector spaces and linear mappings between them is crucial for grasping data structures and transformations.
2. Matrix Algebra: ++Matrices represent linear transformations and are fundamental in computations involving datasets.
3. Eigenvalues and Eigenvectors: These concepts are vital for dimensionality reduction techniques and understanding data variance. [6,7]

B. Introduction to Algebraic Topology

Algebraic topology provides tools to study topological spaces through algebraic invariants. Essential topics include:

1) Simplicial Complexes: These are combinatorial structures that approximate topological spaces and are used to study their properties. A related concept is that of a triangulation. A geometric simplicial complex K is said to be a triangulation of a topological space X, if there exists a homeomorphism : K X. A space that accepts a triangulation is said to be triangulable.[8,9]

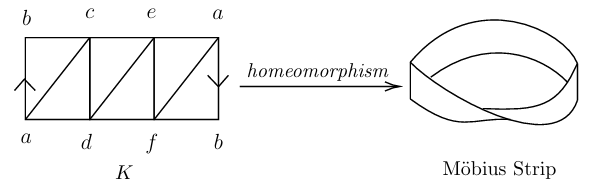
Figure 2: geometric simplicial complex

2) Homology and Cohomology: These theories assign algebraic structures (like groups) to topological spaces, enabling the classification of their features such as holes and voids.

C. Persistent Homology

Persistent homology is a central tool in TDA that studies the multi-scale topological features of data. Key points include:

1. Filtrations: These are nested sequences of simplicial complexes used to analyze data at various scales.
2. Persistence Diagrams and Barcodes: These are visual representations that summarize the birth and death of topological features across scales.[10]

D. Computational Tools and Algorithms

Implementing TDA requires efficient computational methods. Important aspects include:

1. Matrix Reduction Techniques: Algorithms for reducing boundary matrices to compute homology efficiently.
2. Software Libraries: Tools such as GUDHI, Dionysus, and Ripser facilitate TDA computations.[11,12,13,14]

E. Advanced Topics

Depending on the depth of your review, you might also explore:

1. Sheaf Theory: This provides a framework for systematically tracking local data attached to the open sets of a topological space.
2. Category Theory: This offers a high-level abstraction useful for understanding the relationships between different algebraic structures in TDA.[16]

III. METHODOLOGIES AND TECHNIQUES

Here, you delve into the specific algebraic methods and tools employed in topological data analysis, such as persistent homology, simplicial complexes, and other relevant techniques.

A. Simplicial Complexes and Filtrations

1. Simplicial Complexes: These are combinatorial structures that generalize the concept of graphs to higher dimensions, allowing the representation of multi-dimensional data relationships. They serve as the foundational building blocks in TDA for modeling the shape of data.
2. Filtrations: A filtration is a nested sequence of simplicial complexes, each included in the next, used to study the data at multiple scales. By analyzing how topological features evolve across these scales, one can infer significant patterns and structures within the data. [17,18,19]

B. Homology and Persistent Homology

1. Homology: This algebraic tool identifies and quantifies topological features such as connected components, holes, and voids within a space. In TDA, homology is computed over simplicial complexes to understand the underlying structure of data.
2. Persistent Homology: An extension of homology, persistent homology examines how topological features persist across different scales in a filtration. Features that persist over a wide range of scales are often considered significant, distinguishing them from noise.

C. Computational Algorithms

1. Matrix Reduction Techniques: Algorithms such as the Smith Normal Form are employed to reduce boundary matrices, facilitating efficient computation of homology groups. These techniques are crucial for handling large datasets typical in data science applications. [20]
2. Discrete Morse Theory: This method simplifies complex computations by reducing the number of simplices needed to compute homological features, thereby enhancing computational efficiency.

D. Software and Computational Tools

1. GUDHI: An open-source library offering data structures and algorithms for TDA, including simplicial complexes and persistent homology computations.
2. Ripser: A software tool designed for efficient computation of Vietoris–Rips persistence barcodes, particularly useful for large datasets.
3. Dionysus: A library providing implementations for computing persistent homology and cohomology , along with other TDA-related algorithms.[22]

E. Mapper Algorithm

The Mapper algorithm is a technique for visualizing high-dimensional data by constructing a simplicial complex that captures its topological structure.

It involves:

1. Covering the Data: Applying a cover (e.g., overlapping intervals) to the data based on a chosen filter function.
2. Clustering: Performing clustering within each set of the cover to identify connected components.
3. Constructing the Simplicial Complex: Nodes represent clusters, and edges (or higher-dimensional simplices) are added between nodes with shared data points, resulting in a simplicial complex that reflects the data's shape.[23]

F. Advanced Techniques

1. Sheaf Theory: Provides a framework for systematically tracking local data attached to the open sets of a topological space, offering a more refined analysis of data structures.
2. Category Theory: Offers a high-level abstraction useful for understanding the relationships between different algebraic structures in TDA, facilitating the formulation of more general theories and methods. [24]

IV. APPLICATIONS IN DATA SCIENCE

This section explores how the discussed methodologies are applied within data science, providing examples and case studies that demonstrate the practical utility of algebra in topological data analysis. It's essential to illustrate how algebraic methods, particularly those from Topological Data Analysis (TDA), are employed to address complex challenges across various domains within data science and  This section should highlight real-world applications, demonstrating the practical utility and versatility of TDA in extracting meaningful insights from intricate datasets.[25]

A. Image and Signal Processing

1. Feature Extraction: TDA techniques, such as persistent homology, are utilized to identify and quantify topological features within images and signals, aiding in tasks like object recognition and classification.
2. Noise Reduction: The robustness of topological features against noise makes TDA a valuable tool in preprocessing steps, enhancing the quality of image and signal analysis. By focusing on persistent features, TDA helps in distinguishing significant patterns from random noise.[26]

B. Natural Language Processing (NLP)

1. Semantic Structure Analysis: TDA has been applied to uncover the topological structure of semantic spaces, providing insights into the relationships between words and concepts.This approach facilitates tasks such as topic modeling and sentiment analysis by revealing the 'shape' of language data.
2. Document Classification: By representing text data as high-dimensional point clouds, TDA methods can assist in clustering and classifying documents based on their topological features, offering a novel perspective beyond traditional statistical methods.

C. Biosciences

1. Brain Connectomics : TDA has been employed to analyze the complex network of neural connections in the brain, known as connectomes. By studying the topological properties of these networks, researchers can gain insights into brain function and organization.[27]
2. Drug Discovery and Development: In the pharmaceutical industry, TDA has been applied to analyze high-dimensional biological data, aiding in the identification of potential drug targets and understanding the mechanisms of action.
3. Epidemiology and Disease Modeling: TDA methods have been used to study the spread of diseases by analyzing the topological features of epidemiological data, providing insights that can inform public health strategies.[28]

D. Financial Data Analysis

1. Market Structure Analysis: TDA has been applied to understand the 'shape' of financial markets by analyzing the topological features of market data, aiding in the detection of market regimes and transitions.
2. Portfolio Optimization: By examining the topological relationships between different financial instruments, TDA can assist in identifying diversification opportunities and optimizing investment portfolios.[29]

E. Sensor Networks

1. Coverage Analysis: TDA techniques are used to assess the coverage and detect coverage holes in sensor networks, ensuring efficient deployment and operation.
2. Anomaly Detection: By analyzing the topological patterns of sensor data, TDA can help in identifying anomalies and ensuring the reliability of sensor networks.

F. Machine Learning

1. Feature Engineering: TDA provides a framework for creating topological features that can be integrated into machine learning models, enhancing their performance by capturing the intrinsic 'shape' of data. This approach has been shown to improve classification and regression tasks by incorporating topological information.
2. Model Interpretability: The topological perspective offered by TDA can aid in understanding the decision boundaries and behavior of complex machine learning models, contributing to more interpretable and trustworthy AI systems.[30]

V. CURRENT CHALLENGES AND FUTURE DIRECTIONS

Discuss the limitations, ongoing challenges, and potential future developments in the field, offering insights into areas where further research is needed. It's crucial to address the existing limitations within the field and propose potential avenues for future research. This discussion not only highlights areas requiring further development but also underscores the dynamic nature of Topological Data Analysis (TDA) as it continues to evolve and integrate more deeply with data science.

A. Computational Complexity

1. Challenge: The algorithms used in TDA, particularly those involving persistent homology, can be computationally intensive, especially when applied to large, high-dimensional datasets. This complexity can hinder the scalability and real-time applicability of TDA methods.[31]
2. Future Direction: Developing more efficient algorithms and leveraging advanced computational techniques, such as parallel processing and quantum computing, could mitigate these challenges, enabling the application of TDA to increasingly large datasets.

B. Integration with Machine Learning

1. Challenge: While TDA has shown promise in enhancing machine learning models, seamlessly integrating topological features into these models remains a complex task. Determining the most effective ways to combine TDA with deep learning architectures is an ongoing area of research.
2. Future Direction: Advancing the field of topological deep learning (TDL) involves creating novel neural network architectures that inherently incorporate topological concepts, thereby improving model performance and interpretability.

C. Interpretability and Visualization

1. Challenge: The abstract nature of topological constructs can make interpreting and visualizing TDA results challenging for practitioners, potentially limiting the accessibility and adoption of these methods.
2. Future Direction: Developing intuitive visualization tools and user-friendly software that can effectively convey complex topological information will be essential in making TDA more accessible to a broader audience.

D. Theoretical Foundations

1. Challenge: While TDA provides powerful tools for data analysis, the theoretical underpinnings, particularly concerning the stability and robustness of topological invariants in noisy data, require further exploration to ensure reliable application.
2. Future Direction: Conducting rigorous theoretical research to establish stronger foundations for TDA methods will enhance their reliability and facilitate their application across diverse domains.[31]

E. Application to Diverse Data Types

1. Challenge: Extending TDA methods to effectively handle various data types, such as time-series data, multi-modal data, and dynamic networks, presents ongoing challenges due to the inherent complexity and variability of these data forms.
2. Future Direction: Adapting and generalizing TDA techniques to accommodate a wider range of data structures will broaden the applicability of topological methods in data science.

VI. EDUCATIONAL OUTREACH AND INTERDISCIPLINARY COLLABORATION

1. Challenge: The specialized knowledge required to apply TDA methods can be a barrier to entry for researchers and practitioners from other disciplines, potentially limiting interdisciplinary applications.
2. Future Direction: Promoting educational initiatives and fostering collaborations across disciplines will be vital in disseminating TDA knowledge and encouraging its integration into various fields of study.

Conclusion

The integration of algebraic methods within Topological Data Analysis (TDA) has significantly advanced the field of data science by providing innovative tools to uncover the intrinsic \'shape\' of complex datasets. This synergy has enabled more profound insights across various domains, including image processing, natural language processing, biosciences, and financial analysis. Despite these advancements, challenges such as computational complexity, seamless integration with machine learning models, and the need for intuitive visualization tools persist. Addressing these issues through the development of efficient algorithms, the creation of topologically informed neural network architectures, and the enhancement of user-friendly software will be crucial for the continued evolution of TDA. Looking forward, expanding the theoretical foundations of TDA, adapting its methodologies to diverse data types, and fostering interdisciplinary collaborations will be essential steps in fully harnessing the potential of algebraic approaches in data science. By embracing these future directions, the data science community can continue to leverage the strengths of TDA, driving innovation and uncovering deeper insights within complex data structures.

References

[1] Adams, H., Emerson, T., Kirby, M., Neville, R., Peterson, C., Shipman, P., Chepushtanova, S., Hanson, E., Motta, F., Ziegelmeier, L.: Persistence images: A stable vector representation of persistent homology. J. Mach. Learn. Res. 18 (1), 218–252(2017) [2] Adams, H., Tausz, A., Vejdemo-Johansson, M.: Javaplex: A research software pack-age for persistent (co) homology. In: International Congress on Mathematical Soft-ware. pp. 129–136. Springer (2014) [3] Barsocchi, P., Cassarà, P., Giorgi, D., Moroni, D., Pascali, M.: Computational topology to monitor human occupancy. Proceedings 2 (99) (2018) [4] Bauer, U., Kerber, M., Reininghaus, J.: DIPHA (a distributed persistent homology algorithm). Software available at https://github.com/DIPHA/dipha (2014) [5] Bauer, U., Kerber, M., Reininghaus, J., Wagner, H.: PHAT–persistent homology algorithms toolbox. Journal of symbolic computation78, 76–90 (2017) [6] Bergomi, M.G., Frosini, P., Giorgi, D. et al. Towards a topological–geometrical theory of group equivariant non-expansive operators for data analysis and machine learning. Nat Mach Intell 1, 423–433 (2019). [7] Biasotti, S., Cerri, A., Frosini, P., Giorgi, D., Landi, C.: Multidimensional size functions for shape comparison. Journal of Mathematical Imaging and Vision 32 (2) (2008) [8] Bowman, G., Huang, X., Yao, Y., Sun, J., Carlsson, G., Guibas, L., Pande, V.: Structural insight into RNA hairpin folding intermediates. J Am Chem Soc. 130 (30), 9676–8 (2008) [9] Bubenik, P.: Statistical topological data analysis using persistence landscapes. Journal of Machine Learning Research 16 (3), 77–102 (2015) [10] Carlsson, G., Ishkhanov, T., de Silva, V., Zomorodian, A.: On the local behavior of spaces of natural images. International Journal of Computer Vision 76, 1–12 (2008) [11] Ramer, L. M., Ramer, M. S. & Bradbury, E. J. Restoring function after spinal cord injury: towards clinical translation of experimental strategies. Lancet Neurol. [12] 1241–1256 (2014). 11. Manley, G. T. & Maas, A. I. Traumatic brain injury: an international knowledge-based approach. JAMA 310, 473–474 (2013). [13] Lum, P. Y. et al. Extracting insights from the shape of complex data using topology. Sci. Rep. 3, 1236 (2013). [14] Nielson, J. L. et al. Development of a database for translational spinal cord injury research. J. Neurotrauma 31, 1789–1799 (2014). [15] Inoue, T. et al. Combined SCI and TBI: recovery of forelimb function after unilateral cervical spinal cord injury (SCI) is retarded by contralateral traumatic [16] Rosenzweig, E. S. et al. Extensive spontaneous plasticity of corticospinal projections after primate spinal cord injury. Nat. Neurosci. 13, 1505–1510 (2010). [17] Basso, D. M., Beattie, M. S. & Bresnahan, J. C. A sensitive and reliable locomotor rating scale for open field testing in rats. J. Neurotrauma 12, 1–21 (1995). [18] Scheff, S. W., Rabchevsky, A. G., Fugaccia, I., Main, J. A. & Lumpp, Jr J. E. Experimental modeling of spinal cord injury: characterization of a forcedefined injury device. J. Neurotrauma 20, 179–193 (2003). [19] Young, W. Spinal cord contusion models. Prog. Brain Res. 137, 231–255 (2002). [20] Subramanian, A. et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl Acad. Sci. USA 102, 15545–15550 (2005). [21] Cohen, J. A power primer. Psychol. Bull. 112, 155–159 (1992). [22] MacCallum, R. C., Roznowski, M. & Necowitz, L. B. Model modifications in covariance structure analysis: the problem of capitalization on chance. Psychol. Bull. 111, 490–504 (1992). [23] Hawryluk, G. W. et al. Mean arterial blood pressure correlates with neurological recovery following human spinal cord injury: analysis of high frequency physiologic data. J. Neurotrauma doi:10.1089/neu.2014.3778 (2015). [24] Inoue, T., Manley, G. T., Patel, N. & Whetstone, W. D. Medical and surgical management after spinal cord injury: vasopressor usage, early surgerys, and complications. J. Neurotrauma 31, 284–291 (2014). [25] Guha, A., Tator, C. H. & Rochon, J. Spinal cord blood flow and systemic blood pressure after experimental spinal cord injury in rats. Stroke 20, 372–377 (1989). [26] Kong, C. Y. et al. A prospective evaluation of hemodynamic management in acute spinal cord injury patients. Spinal Cord 51, 466–471 (2013). [27] Scallan, J., Huxley, V. H. & Korthuis, R. J. Capillary Fluid Exchange: Regulation, Functions, and Pathology (Morgan & Claypool Life Sciences, 2010). [28] Gorelick, P. B. New horizons for stroke prevention: PROGRESS and HOPE. Lancet Neurol. 1, 149–156 (2002). [29] Choi, D. W. Excitotoxic cell death. J. Neurobiol. 23, 1261–1276 (1992). [30] Crowe, M. J., Bresnahan, J. C., Shuman, S. L., Masters, J. N. & Beattie, M. S. Apoptosis and delayed degeneration after spinal cord injury in rats and monkeys. Nat. Med. 3, 73–76 (1997). [31] Ferguson, A. R. et al. Derivation of multivariate syndromic outcome metrics for consistent testing across multiple models of cervical spinal cord injury in rats. PLoS ONE 8, e59712 (2013).

Copyright

Copyright © 2025 Asmaa Mohammed Ashour Kushlaf. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.