Apprentice of Ground Water Level Fluctuation using AI Models in Jammu District of Jammuand Kashmir

Abstract

Gravity causes precipitation to permeate and percolate into subterranean aquifers through bedrock interstices, sands, gravels, and other interspaces, which hold the majority of the freshwater found beneath the earth\'s surface (Wang et al., 2014). There are 1.4 billion cubic meters of water on the earth. Fresh water makes up 2.5 percent of it, and the oceans and seas make up 97.5 percent. According to Unes et al. (2017), sweet waters account for 0.3% of the water in lakes and rivers, 30.8% of ground water, soil necropsy, and marsh, and 68.9% of ice and permanent snow. India has 430.45 km3 of yearly replenishable groundwater resources and 395.52 km3 of net annual groundwater availability. According to Anonymous (2013), Jammu and Kashmir has yearly replenishable groundwater resources of 3.70 km3, with a net annual groundwater availability of 3.33 km3. It has been anticipated that the nation will need 1450 km3/year of water overall by the year 2050 for a variety of activities (Gupta and Deshpande 2004). Around 2050, water availability will need to be almost tripled compared to the current 500 km3/year. Particularly in arid and semi-arid areas, groundwater represents a substantial supply of fresh water for industry, agriculture, and drinking (Barzegar et al., 2017). Groundwater supplies are under pressure to meet the demand for fresh water across several industries, since surface water pollution is getting worse every day. Both groundwater quality and quantity have lately declined as a result of excessive groundwater extraction for business and agriculture (Kalantari et al., 2019). In addition, human activity and climate change are having an effect on the amount and quality of supply (Kalantari et al., 2014). Since the conclusion of the green revolution, more groundwater has been extracted nationwide in India, leading to overuse in certain states, including Tamil Nadu, Orissa, Punjab, Rajasthan, Gujrat, and Haryana (CGWB, 2006). As a result, a sizable population and their means of subsistence are in jeopardy, greatly endangering the natural ecology, the security of India\'s food and water supplies, and the health of its plants and people. It emphasizes how important it is to manage groundwater resources sustainably in order to meet the needs of both the current and the next generation. Thanks to recent rapid increases in computing power and widespread availability of computers and model software, groundwater modelling has become an essential tool for professional hydro-geologists to identify, develop, and manage groundwater resources as well as to predict the effects of management measures (Brassington, 1998). Forecasting groundwater levels (GWLs) can reduce groundwater misuse and aid in the creation of efficient water resource management plans (Yoon et al., 2011). Models like MODFLOW, FEFLOW, and PMWIN have been developed to estimate groundwater levels and recharge for global groundwater research. According to Raghavendra and Deka (2016), GWL forecasting can be used to manage groundwater for a range of demands, evaluate changes in GW storage, estimate recharge rates, and guarantee the ecological sustainability of a watershed.

Introduction

I. INTRODUCTION

In recent decades, several studies have examined various physical, numerical, and data-driven methods for predicting groundwater levels. However, creating numerical models calls for a massive amount of data as well as other information. Getting a lot of these data and information is often expensive and/or difficult, especially in developing countries. Researchers are now more inclined to use machine learning approaches because of the aforementioned practical difficulty (Adamowski and Chan 2011; Nayak et al., 2006). Artificial intelligence (AI) models have garnered significant interest in the past two decades due to their advantages over numerical models and their capacity to predict intricate hydrologic systems (Gong et al., 2016). Neural networks (NNs) have been utilized successfully in forecasting GWLs due to their capacity to handle complicated nonlinear difficulties that are challenging to solve using conventional parametric methods (Mohanty et al., 2010; Suryanarayana et al., 2014).

In addition to applying AI techniques, researchers have started to relate wavelet transforms (WT) with the previously described model types. Before the data is fed into the data-driven models, WT is employed as a data pre-processing tool in connected models (Belayneh et al., 2016). Hydrological studies are increasingly using coupled wavelet-artificial neural network (WA-ANN) models for forecasting (Adamowski and Chan, 2011; Barzegar et al., 2016), trend analysis (Nalley et al., 2012), and multiscale correlation (Labat, 2005; Sang et al., 2010). A variety of algorithms can be used to train neural network models, including gradient descent (GD), gradient descent with momentum (GDM), gradient descent with Adaptive learning rate back propagation (GDA), one-step secant (OSS), scaled conjugate gradient (SCG), Fletcher-Reeves conjugate gradient (CGF), Powell-Beale conjugate gradient (CGB), and Polak Ribiere conjugate gradient methods (Sudheer and Mathur, 2012). Huang et al. (2004) introduced the single layer feed forward neural network (SLFN), an extreme learning machine (ELM). The ELM model preserves the benefits of quick learning, robust generalization, and simple parameter selection when compared to the back-propagation (BP) neural network, support vector machines, and other traditional models (Huang et al., 2006; Lian et al., 2014). Consequently, several fruitful studies into applying the ELM algorithm to problems across several scientific domains have been finished (Yu et al., 2014; Wong et al., 2015). In order to determine a relationship between input and output variables and choose the best model or network topology, the GMDH is an inductive learning algorithm that makes use of quadratic regression polynomials with two input variables (DeGiorgi et al., 2016). By providing an objective model of a high-order polynomial in the input variable, it solves a variety of problems, including prediction, identification, control, and so on. It then generates, verifies, and chooses from a large number While there are still few applications of the GMDH algorithm for groundwater studies, its use in artificial intelligence models is becoming more and more popular, especially in the field of hydrology. The creation of the WA-ELM and WA-GMDH models, which combine the advantages of several wavelets to anticipate groundwater levels, is what makes this work unique.

II. STUDY AREA

There are two administrative divisions in the Jammu and Kashmir Union Territory: the Kashmir division (Anantnag, Baramulla, Kupwara, Kulgam, Pulwama, Srinagar, Shopian Bandipora, Budgam, Ganderbal) and the Jammu division (Jammu, Kathua, Reasi, Rajouri, Poonch, Samba, Udhampur, Ramban, Kishtwar, Doda). Between latitudes 32°17' and 36°08' N and longitudes 73°23' and 76°47' E is where it is situated.

The Central Groundwater Board, North Western Himalayan Region, checks the water levels at observation wells in the state of Jammu and Kashmir four times a year: in May (between May 20 and May 31), August (between August 20 and August 31), November (1 and 10), and January (1 and 10).

III. METHODOLOGY

Creating appropriate artificial intelligence (AI) models to forecast fluctuations in groundwater levels can be a useful use of machine learning. In this situation, supervised and unsupervised machine learning techniques can both be applied. The processes to create these models using these methods are outlined below.

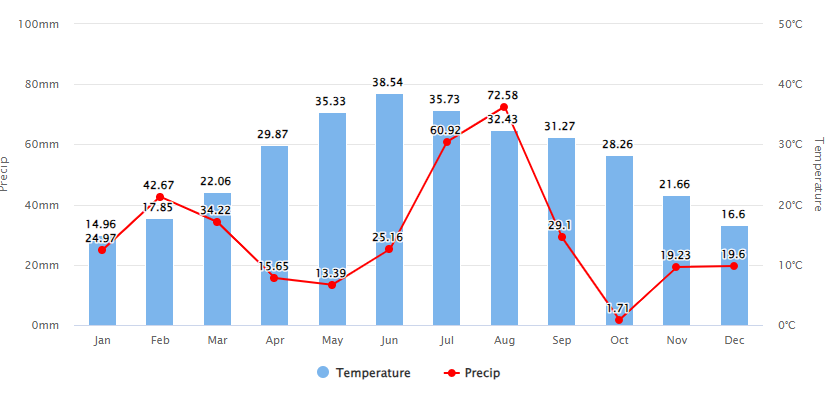
The chart above shows the mean monthly temperature and precipitation of Akhnoor in recent years.

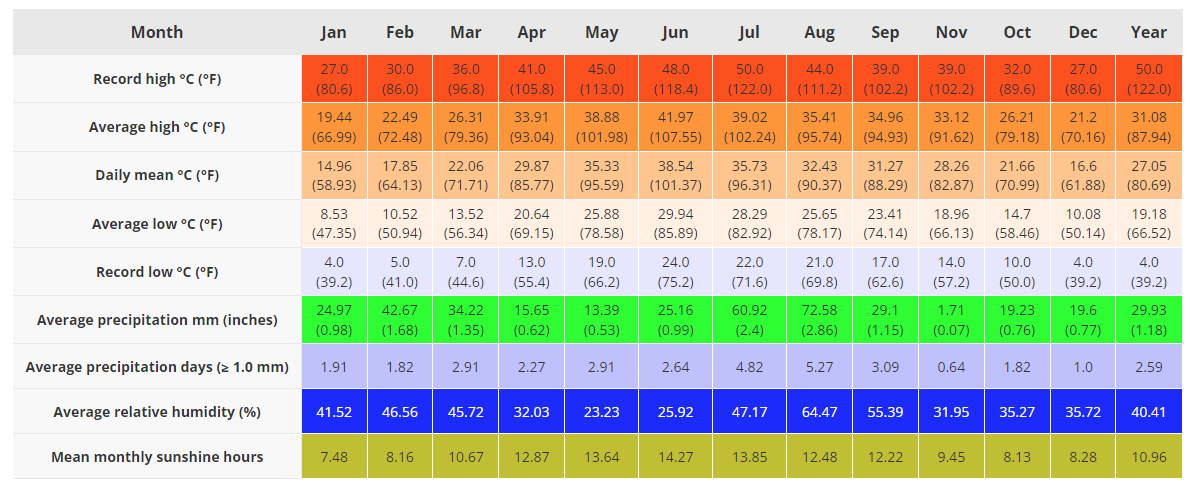Weather of Akhnoor by months

1) Gathering and Preparing Data

• Compile historical data on groundwater levels from a variety of monitoring wells and pertinent meteorological and environmental parameters, like temperature, precipitation, and groundwater extraction rates.
• Handle mistakes, outliers, and missing numbers to clean up the data.
• Scale or normalize the data to guarantee that the ranges of each feature are comparable.

2) Engineering Features:

• Determine significant elements, such as hydrological factors, geological traits, and seasonal patterns, that may have an impact on groundwater levels.
• Create derived features using domain expertise to increase the models' capacity for prediction.

3) Data Division

• Divide the data into sets for testing, validation, and training. The testing set assesses the final performance, the validation set aids in hyper-parameter tweaking, and the training set is utilized to train the models.

4) Approaches to supervised and unsupervised machine  learning

• There are distinct benefits to using both supervised and unsupervised machine learning techniques for forecasting variations in groundwater levels. While the unsupervised technique concentrates on identifying hidden structures and relationships without depending on labelled samples, the supervised approach enables direct prediction by learning from labelled data.
• A supervised machine learning approach uses historical data with known groundwater levels as a reference to train the model in the context of forecasting fluctuations in groundwater levels. Developing a predictive model that can generalize and produce precise forecasts for data that hasn't been seen is the aim. This method requires labelled data, which means that every data point in the training set needs to have measurements of the relevant groundwater levels along with the characteristics (such temperature, rainfall, etc.).
• The prediction model can be created using supervised regression methods including Gradient Boosting, Support Vector Machines (SVM), Decision Trees, Random Forests, and Linear Regression. Every algorithm has pros and cons, and the best-performing model can be found by carefully analysing each one using measures like Mean Absolute Error (MAE) or Root Mean Squared Error (RMSE).
• The model can be used to forecast variations in groundwater levels in real-time or almost real-time scenarios after it has been trained and verified on the testing set. Frequent retraining with fresh data guarantees that the model stays current and accurate, allowing it to adjust to shifting environmental circumstances.
• To guarantee a clean dataset, missing values and outliers are treated during the initial stage of the unsupervised technique, known as data preprocessing. Once labelled groundwater level data are no longer required, the emphasis switches to identifying innate patterns and connections between the features.
• A well-liked unsupervised method called K-Means Clustering puts related data points together according to feature similarity. This can assist in locating specific areas within the dataset that correspond to certain behaviours of groundwater levels. DBSCAN (Density-Based Spatial Clustering of Applications with Noise), another helpful technique, can spot high-density areas, which may indicate locations with notable fluctuations or anomalies.

A mix of these methods or a prevailing method can provide more precise forecasts and a deeper comprehension of groundwater behaviour, depending on the particular goals and data at hand. Frequent updates and enhancements to the models guarantee these AI-powered systems' effectiveness in efficiently managing water resources.

To ascertain the degree of inaccuracy associated with the model output, many criteria can be employed to evaluate the proficiency of black-box models in hydrological modelling (Gupta et al. 2009). The performance of the trained model will be compared using a statistical precision assessment. This study will employ the Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Correlation Coefficient (R) to evaluate the models' predictive potential. The given parameters are presented as

• RMSE, or root mean square error - When we talk about RMSE, we are talking about the sample standard deviation of the difference between predicted and actual values. It has the following definition:

• R, or the correlation coefficient - The degree to which the models agree with the experimental results is shown by the correlation coefficient (R). It is stated as

• The MAE, or mean absolute error - Mean absolute error (MAE) provides the mean of the absolute difference between the target value and the model prediction. The MAE calculates the magnitude of mistakes in a sequence of predictions without taking into account their sign. It's stated as

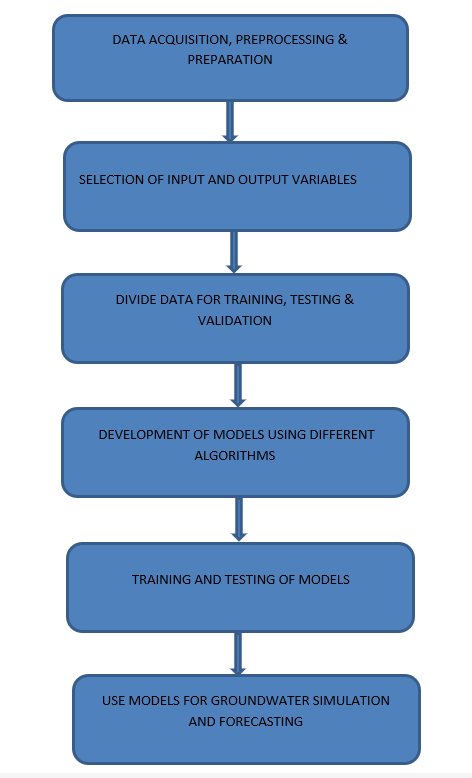
FLOW CHART

Conclusion

The Akhnoor district\'s long-term groundwater level monitoring and rainfall data have shown that variations in groundwater levels may directly affect groundwater management techniques. It was discovered that abstraction, lateral groundwater flow through regional circulation, and direct and induced recharge all contributed to the groundwater-level fluctuation pattern. One plausible long-term indicator has been the consistent variation in the amplitude of the water level. In regions where groundwater is predominantly utilized for water supply, estimating groundwater recharge is crucial. Groundwater resources are subject to pollution and are extensively used for irrigation and other uses. Gradient Boosting Regression was used to develop a regression model. The model was trained to estimate groundwater level using rainfall as inputs. Using the model, it is possible to identify the reasons producing groundwater variability in the area under study. The groundwater level and primary components have a linear relationship, which was satisfied by the actual values of the groundwater level compared to the estimated values.

References

[1] Adamowski, J., Chan, H.F. (2011). A wavelet neural network conjunction model for groundwater level forecasting. J. Hydrol. 407, 28–40. [2] Anonymous, 2013-2014. Ground Water year Book. Ministry of Water Resources. Government of India, New Delhi. [3] Barzegar, R., Adamowski, J., Asghari Moghaddam, A. (2016). Application of wavelet-artificial intelligence hybrid models for water quality prediction: a case study in AjiChay River, Iran. Stoch. Env. Res. Risk A. 30 (7), 1797–1819. [4] Barzegar, R., Asghari Moghaddam, A., Tziritis, E., Fakhri, M.S., Soltani, S. (2017). Identification of hydrogeochemical processes and pollution sources of groundwater resources in the Marand plain, northwest of Iran. Environ. Earth Sci. 76, 297. [5] Belayneh, A., Adamowski, J., Khalil, B., Quilty, J. (2016). Coupling machine learning methods with wavelet transforms and the bootstrap and boosting ensemble approaches for drought prediction. Atmos. Res. 172–173, 37–47. [6] Bisht, D., Mohan, R. M. and Joshi, M. (2009) Simulation of water table elevation fluctuation using fuzzy-logic and ANFIS. Comput Model New Technol 13(2):16–23. [7] Brassington, R. 1998. Field Hydrogeology. Second edition 1998 Published John Wiley & Sons. Chichester. [8] Bustami, R., Bessaih, N., Bong, C. and Suhaili, S. (2006). Artificial Neural Network for Precipitation and water level predictions of Bed up River. IAENG International Journal of Computer Sciences. 34(2): 11-19. [9] DeGiorgi, M.G., Malvoni, M., Congedo, P.M. (2016). Comparison of strategies for multistep ahead photovoltaic power forecasting models based on hybrid group method of data handling networks and least square support vector machine. Energy 107, 360–373. [10] CGWB, 2006. Dynamic Groundwater Resources of India. (as on March 2004). Central Ground Water Board (CGWB), Ministry of Water Resources, New Delhi, India. [11] Emamgholizadeh, S., Moslemi, K. &Karami, G. (2014) Prediction the Groundwater Level of Bastam Plain (Iran) by Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS). Water Resour Manage 28, 5433–5446. https://doi.org/10.1007/s11269-014-0810-0. [12] Ghose, D., Das, U., Roy, P. (2018). Modeling response of runoff and evapotranspiration for predicting water table depth in arid region using dynamic recurrent neural network. Groundwater for. Sustain. Dev. 6, 263–269. https://doi.org/10.1016/j.gsd.2018.01. 007. [13] Gong, Y., Zhang, Y., Lan, S., Wang, H. (2016). A comparative study of artificial neural networks, support vector machines and adaptive neuro fuzzy inference system for forecasting groundwater levels near Lake Okeechobee, Florida. Water Resour. Manag. 30 (1), 375–391. [14] Gupta, H. V., Kling, H., Yilmaz, K. K., Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: implications for improving hydrological modelling. J Hydrol 377(1–2):80–91. [15] Gupta, S. K. and Deshpande, R. D. (2004). Water for India in 2050: first-order assessment of available options. Current Science. 86(9): 1216-1224. [16] Huang, G.B., Zhu, Q.Y., Siew, C.K. (2004). Extreme learning machine: a new learning scheme of feedforward neural networks. International Joint Conference on Neural Networks. 2, pp. 985–990. [17] Huang, G.B., Zhu, Q.Y., Siew, C.K. (2006). Extreme learning machine: theory and applications. Neurocomputing 70 (1), 489–501. [18] Husn, N. E. A., Bari, S. H., Shourov, M. H., Tauhid, M. and Rahman, U. (2016). Groundwater level prediction using artificial neuron network. International Journal of Hydrology Science and Technology, 6(4): 371-381. [19] Jeihouni, E., Eslamian, S., Mohammadi, M. and Zareien, J. M. (2019). Simulation of groundwater level fluctuations using a wavelet-ANN hybrid technique for the Shabestar plain, Iran, 78: 293. [20] Kalantari Z, Lyon SW, Folkeson L, French HK, Stolte J, Jansson P-E, Sassner M (2014) Quantifying the hydrological impact of simulated changes in land use on peak discharge in a small catchment. Sci Total Environ 466:741–754. [21] Kalantari Z, Ferreira CSS, Page J, Goldenberg R, Olsson J, Destouni G (2019) Meeting sustainable development challenges in growing cities: coupled social-ecological systems modeling of land use and water changes. J Environ Manag 245:471–480. [22] Kumar, D., Roshni, T., Singh, A., Jha, M. K. and Samui, P. (2020). Predicting groundwater depth fluctuations using deep learning, extreme learning machine and Gaussian process: a comparative study. Earth Sci Inform. 13,1237-1250. [23] Labat, D. (2005). Recent advances in wavelet analyses: part 1. A review of concepts. J. Hydrol. 314 (1–4), 275–288. [24] Lambert, R.S.C., Lemke, F., Kucherenko, S.S., Song, S., Shah, N. (2016). Global sensitivity analysis using sparse high dimensional model representations generated by the group method of data handling. Math. Comput. Simul. 128, 42–54. [25] Lian, C., Zeng, Z., Yao, W., Tang, H. (2014). Extreme learning machine for the displacement prediction of landslide under rainfall and reservoir level. Stoch. Env. Res. Risk A. 28, 1957–1972. [26] Mohanty, S., Jha, M. K., Kumar,A., Srivastava, R. C. and James, B. K. (2007). Groundwater level forecasting in Kathajodi River basin using artificial neural network. Third International Groundwater Conference (IGC-2007), held at TNAU, Coimbatore, India, TS-5-12. [27] Mohanty, S., Jha, M.K., Kumar, A., Sudheer, K.P. (2010). Artificial neural network modeling for groundwater level forecasting in a River Island of eastern India. Water Resour. Manag. 24, 1845–1865. [28] Mohanty, S., Jha, M.K., Kumar, A., Sudheer, K.P. (2010). Artificial neural network modeling for groundwater level forecasting in a River Island of eastern India. Water Resour. Manag. 24, 1845–1865. [29] Nair, S. S. and Sindhu, G. (2016). Groundwater level forecasting using Artificial Neural Network. International Journal of Scientific and Research Publications, Vol: 6(1): 234-238. [30] Nalley, D., Adamowski, J., Khalil, B. (2012). Using discrete wavelet transforms to analyze trends in streamflow and precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 475, 204–228. [31] Nayak PC, Rao YS, Sudheer K (2006) Groundwater level forecasting in a shallow aquifer using artificial neural network approach. Water Resour Manag 20(1):77–90 [32] Piasecki, A., Jakub, J. and Rajmund, S. (2017). Forecasting Surface Water level Fluctuations of Lake Serwy (Northeastern Poland) by Artificial Neural Networks and Multiple Linear Regression, Vol: 25(04): 379-388. https://doi.org/10.3846/16486897.2917.1303498. [33] Raghavendra, N. S., Deka, P. C. (2016). Multistep ahead groundwater level time-series forecasting using Gaussian process regression and ANFIS. Advanced Computing and Systems for Security, Volume 396 of the Series Advances in Intelligent Systems and Computing, pp. 289–302. [34] Sahoo, S., Russo, T. A., Elliott, J. and Foster, I. (2017). Water Resources Machine learning algorithms for modeling groundwater level changes in agricultural regions of the U.S. Journal of Water Resoyrce Research. Doi:10.1002/2016wr19933. [35] Sang, Y.F., Wang, D., Wu, J.C., Zhu, Q.P. (2010). Wavelet cross-correlation method for hydrologic time series analysis. J. Hydrol. Eng. 11, 1172–1179. [36] Sreekanth , P. D., Geethanjali, N., Sreedevi, P. D., Ahmed, S., Kumar, N. R. and Kamala Jayathi, P. D. (2009). Forecasting groundwater level using artificial neural networks. Current Science, 96(7): 10.

Copyright

Copyright © 2024 Dr. Bashir Ahmad Pandit. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.