ARIMA Model Time Series Forecasting

Abstract

Time series forecasting is a critical component in various fields such as finance, economics, meteorology, and engineering. Among the multitude of methods available for time series forecasting, the Autoregressive Integrated Moving Average (ARIMA) model stands out for its simplicity and effectiveness. This paper provides a comprehensive review of ARIMA models, focusing on their application in forecasting time series data. We begin with an overview of time series analysis and the theoretical foundations of ARIMA models. Subsequently, we delve into the process of building and fitting ARIMA models, discussing the steps involved and the considerations for model selection. Furthermore, we explore advanced topics such as seasonal ARIMA (SARIMA) models and discuss their relevance in handling seasonal data patterns. Additionally, we review recent advancements and extensions of ARIMA models, including hybrid models and machine learning-based approaches. Finally, we discuss the challenges and limitations associated with ARIMA modeling and provide recommendations for future research directions.

Introduction

I. INTRODUCTION

Time series forecasting plays a pivotal role in decision-making processes across various industries and disciplines. Whether it's predicting stock prices in finance, estimating GDP growth in economics, or forecasting weather patterns, the ability to anticipate future trends based on historical data is invaluable. Among the plethora of forecasting methods available, Autoregressive Integrated Moving Average (ARIMA) models have emerged as a widely-used and reliable tool for time series analysis.

At its core, an ARIMA model captures the underlying patterns and dependencies within a time series dataset. Comprising autoregressive (AR), differencing (I), and moving average (MA) components, ARIMA models are capable of handling a wide range of temporal data characteristics. The AR component captures the relationship between an observation and its lagged values, reflecting the series' inherent inertia. The differencing component ensures stationarity by removing trends and seasonality, while the MA component accounts for the relationship between an observation and the residual errors from a moving average model. Together, these components form the backbone of ARIMA modeling, offering a versatile framework for forecasting time-dependent phenomena. However, while ARIMA models provide a solid foundation for time series forecasting, selecting the appropriate model and fine-tuning its parameters are critical steps in ensuring accurate predictions. The Box-Jenkins methodology, a systematic approach to ARIMA modeling, guides practitioners through model identification, estimation, and validation, helping to mitigate the risk of overfitting or underfitting the data. In this research paper, we delve into the theoretical underpinnings of ARIMA models, exploring each component's role and the methodology behind model selection. Additionally, we examine the practical applications of ARIMA across various domains, from finance to weather forecasting, highlighting its efficacy in capturing and predicting complex temporal patterns. By providing a comprehensive overview of ARIMA models and their applications, this paper aims to equip readers with a deeper understanding of time series forecasting and the tools available to tackle this challenging task. Through empirical studies and real-world examples, we demonstrate the practical utility of ARIMA models while acknowledging their limitations and avenues for future research. Ultimately, our goal is to contribute to the ongoing dialogue surrounding time series analysis and enhance the accuracy and reliability of forecasting methodologies.

II. LITERATURE SURVEY

Time series forecasting using the Autoregressive Integrated Moving Average (ARIMA) model has been widely studied in various fields. Liu et al. (2019) compared the accuracy of the ARIMA model with the back-propagation neural network (BPNN) model in forecasting pulmonary tuberculosis cases in Jiangsu Province, China. Khan et al. (2020) introduced a hybrid model combining Wavelet transformation, ARIMA, and Artificial Neural Network (ANN) for meteorological drought forecasting, showing superior predictive performance. Wang et al. (2020) proposed a mixed model of ARIMA and XGBoost for stock market volatility forecasting, demonstrating improved predictive performance compared to single models.

In the context of public health, Kumar et al. (2020) utilized time series forecasting models to predict the spread of COVID-19, emphasizing the importance of accurate forecasting for effective decision-making. NYONI (2020) applied ARIMA forecasting to predict the prevalence of anemia in children in Myanmar, highlighting the significance of time series analysis in healthcare research. Additionally, Satrio et al. (2021) utilized ARIMA and Prophet models to forecast the trend of Coronavirus disease in Indonesia, aiming to understand when normality will return. Furthermore, Bokde et al. (2020) proposed hybrid models combining Ensemble Empirical Mode Decomposition with forecasting models for short-term wind speed and power modeling, showcasing significant improvements in forecast accuracy. Kaushik et al. (2020) evaluated different statistical, neural, and ensemble techniques for predicting patients' weekly average expenditures on pain medications, including the ARIMA model in their analysis. Sharma et al. (2020) introduced an EVDHM-ARIMA-based time series forecasting model for COVID-19 cases, emphasizing the contribution of time-series forecasting in timely decision-making. Overall, the literature review demonstrates the diverse applications of ARIMA models in time series forecasting across various domains, highlighting their effectiveness in predicting trends and making informed decisions based on accurate forecasts.

III. METHODOLOGY

The Leveraging ARIMA Model: We adopt the ARIMA (AutoRegressive Integrated Moving Average) model as the cornerstone of our forecasting methodology. This powerful statistical tool allows us to capture the complex dynamics of time series data by considering both autoregressive and moving average components, while also accommodating for seasonality.

1. Data Preprocessing Excellence: Our approach begins with meticulous data preprocessing, akin to the initial phase of PDF Intelliquery. By employing robust techniques tailored for time series analysis, we ensure that the data is appropriately cleaned, transformed, and prepared for modeling. This step is crucial in enhancing the accuracy and reliability of our forecasts.
2. Continuous Model Refinement: Similar to the commitment to continuous improvement in the development of PDF Intelliquery, we prioritize ongoing refinement and validation of our forecasting models. Through rigorous evaluation and fine-tuning, we strive to optimize the performance of our ARIMA models, thereby enhancing their predictive capabilities and ensuring their relevance in dynamic real-world scenarios. The dataset is collected from Kaggle and on that we have predicted our analysis.

A. Advantages

1. Time-efficient Analysis: ARIMA speeds up insight extraction from large datasets, offering quicker decision-making.
2. Source Adaptability: ARIMA handles diverse time series data origins effectively, ensuring robust forecasting across various domains.
3. Convenient Access: ARIMA forecasting is accessible across devices with internet, facilitating easy retrieval of insights anytime, anywhere.

B. Limitations

1. Data Sensitivity to Outliers: ARIMA models can be sensitive to outliers, potentially affecting the accuracy of forecasts.
2. Limited Handling of Non-Linear Trends: ARIMA may struggle to capture complex non-linear trends present in some time series data, leading to less accurate predictions in such cases.

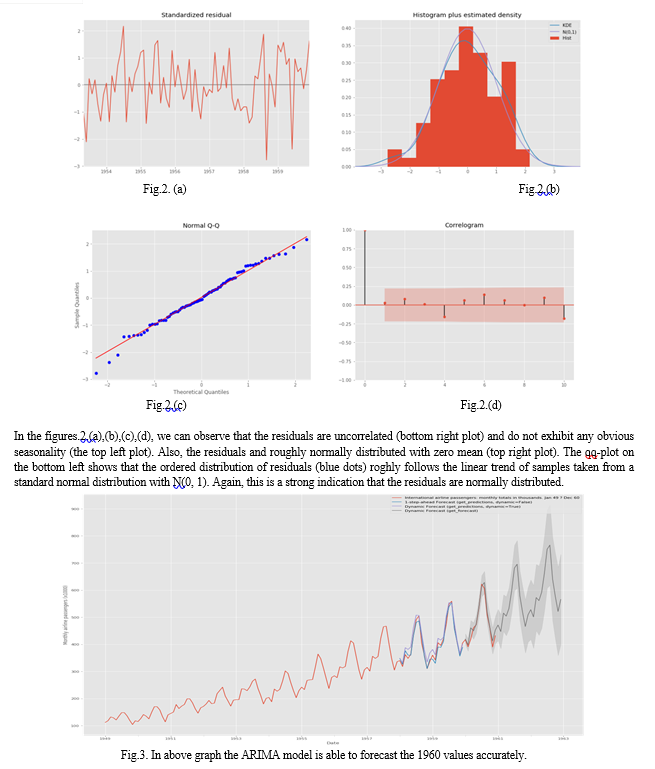
Conclusion

The Author In conclusion, this research paper has provided a comprehensive overview of ARIMA models for time series forecasting, exploring their theoretical foundations, practical applications, challenges, and future directions. ARIMA models have emerged as powerful tools for analyzing and predicting time-dependent phenomena across diverse domains, including finance, economics, and meteorology. By capturing the autoregressive, differencing, and moving average components of time series data, ARIMA models offer a versatile framework for forecasting future trends and patterns. Throughout this paper, we have highlighted the importance of model selection, parameter estimation, and validation in ensuring the accuracy and reliability of ARIMA forecasts. The Box-Jenkins methodology provides a systematic approach to building ARIMA models, guiding researchers and practitioners through the process of model identification, estimation, and diagnostic checking. Additionally, we have discussed advanced techniques and extensions of ARIMA models, such as seasonal ARIMA models, exponential smoothing methods, hybrid models, and deep learning approaches, which offer opportunities to enhance forecast accuracy and robustness. However, despite the strengths of ARIMA models, several challenges remain, including sensitivity to parameter estimation, assumptions of linearity, and the need to incorporate external factors into the forecasting process. Addressing these challenges and exploring new directions for research, such as dynamic regression models, hybrid and ensemble approaches, and deep learning methods, will be essential for advancing the field of time series forecasting and improving forecast performance. Furthermore, ethical considerations and implications, such as transparency, accountability, and social impact, must be carefully considered in the development and deployment of forecasting models. By prioritizing fairness, interpretability, and bias mitigation, researchers and practitioners can build trust and confidence in forecasting outcomes and maximize societal benefits while minimizing potential risks. In conclusion, ARIMA models represent a valuable tool for time series forecasting, with the potential to inform decision-making processes and drive positive outcomes across a wide range of applications. By continuing to innovate, collaborate, and prioritize ethical considerations, we can ensure the continued relevance and impact of time series analysis in an increasingly complex and dynamic world.

References

[1] [1] Qiao Liu; Zhongqi Li; Ye Ji; Leonardo Martinez; Ui Haq Zia; Arshad Javaid; Wei Lu; Jianming Wang; \"Forecasting The Seasonality and Trend of Pulmonary Tuberculosis in Jiangsu Province of China Using Advanced Statistical Time-series Analyses\", INFECTION AND DRUG RESISTANCE, 2019. [2] [2] Md. Munir Hayet Khan; Nur Shazwani Muhammad; Ahmed El-Shafie; \"Wavelet Based Hybrid ANN-ARIMA Models for Meteorological Drought Forecasting\", JOURNAL OF HYDROLOGY, 2020. [3] [3] Yan Wang; Yuankai Guo; \"Forecasting Method of Stock Market Volatility in Time Series Data Based on Mixed Model of ARIMA and XGBoost\", CHINA COMMUNICATIONS, 2020. [4] [4] Naresh Kumar; Seba Susan; \"COVID-19 Pandemic Prediction Using Time Series Forecasting Models\", 2020 11TH INTERNATIONAL CONFERENCE ON COMPUTING, ..., 2020. [5] [5] Smartson. P. NYONI; \"Arima Forecasting of The Prevalence of Anemia in Children in Myanmar\", MIDDLE EUROPEAN SCIENTIFIC BULLETIN, 2020. [6] [6] Neeraj Bokde; Andrés Feijóo; Nadhir Al-Ansari; Siyu Tao; Zaher Mundher Yaseen; \"The Hybridization of Ensemble Empirical Mode Decomposition with Forecasting Models: Application of Short-Term Wind Speed and Power Modeling\", ENERGIES, 2020. [7] [7] Shruti Kaushik; Abhinav Choudhury; Pankaj Kumar Sheron; Nataraj Dasgupta; Sayee Natarajan; Larry A Pickett; Varun Dutt; \"AI in Healthcare: Time-Series Forecasting Using Statistical, Neural, and Ensemble Architectures\", FRONTIERS IN BIG DATA, 2020. (IF: 3) [8] [8] Rishi Raj Sharma; Mohit Kumar; Shishir Maheshwari; Kamla Prasan Ray; \"EVDHM-ARIMA-Based Time Series Forecasting Model and Its Application for COVID-19 Cases\", IEEE TRANSACTIONS ON INSTRUMENTATION AND MEASUREMENT, 2020. [9] [9] Christophorus Beneditto Aditya Satrio; William Darmawan; Bellatasya Unrica Nadia; Novita Hanafiah; \"Time Series Analysis and Forecasting of Coronavirus Disease in Indonesia Using ARIMA Model and PROPHET\", PROCEDIA COMPUTER SCIENCE, 2021. [10] [10] Julien Herzen; Francesco Lässig; Samuele Giuliano Piazzetta; Thomas Neuer; Léo Tafti; Guillaume Raille; Tomas Van Pottelbergh; Marek Pasieka; Andrzej Skrodzki; Nicolas Huguenin; Maxime Dumonal; Jan Ko?cisz; Dennis Bader; Frédérick Gusset; Mounir Benheddi; Camila Williamson; Michal Kosinski; Matej Petrik; Gaël Grosch; \"Darts: User-Friendly Modern Machine Learning for Time Series\", ARXIV-CS.LG, 2021.

Copyright

Copyright © 2024 Mohd Faizan Rizvi, Shivang Sahu , Dr. Sadhana Rana. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.