Automating Branch Change: Developing an Efficient Algorithm for Solving the Branch Change Problem

Abstract

The B.Tech program\'s Branch Change Problem is a key component, giving students the chance to transfer to their desired branch after the first year based on their performance. Since the academic division now solves this issue by hand, there is a possibility of inaccuracy, and it takes a lot of time and effort. In order to overcome these difficulties, the goal of this research is to create a computer algorithm that can successfully solve the branch change problem. The program will minimize the time and effort needed for resolution by automating the process, minimizing the chances of human error. The suggested method would improve branch allocation\'s efficiency and accuracy overall, guaranteeing a fair and efficient process for students looking to switch branches.

Introduction

I. INTRODUCTION

After the first year, every B.Tech student has the option to request a branch change. If the transfer does not contravene the guidelines established by the Institute Senate, the candidate may receive their preferred branch based on how well they performed in the first year. The Branch Change Problem is what we refer to it as. The academic division of our Institute has been manually resolving this issue ever since it was founded. When done manually, there is a high risk of mistakes and a high cost of time. Therefore, the goal of this project is to create a computer algorithm that can address the branch change issue.

A. Organization of The Report

A general overview of the issue and the need for a solution is provided in this chapter. The remaining chapters are set up as follows: In the following chapter, we will understand the problem in greater depth. In Chapter 3, we discuss the allocation verifier approach we have worked on. In Chapter 4, we go through the research papers we have studied and see how they will help us solve our problem. In Chapter 5, we discuss the algorithm designed using the ESDA approach, which we have adapted from the research papers studied, and we see the implementation of this algorithm and finally, in Chapter 6, we conclude with some future work.

II. UNDERSTANDING THE PROBLEM

A. Rules of Branch Change

The Senate of the Indian Institute of Technology and the Vellore Institute of Technology has established the following rules that must be followed in order for a change of branch to be permitted:

1. Depending on the number of openings, all students who successfully completed the First and Second semesters of the course will be eligible for consideration for change of branch.
2. The first year's performance will serve as the foundation for any branch change considerations. In case of a tie in CGPA, the Entrance rank is used.
3. When changing branches, a class's strength cannot drop below the current strength by more than 10% of the sanctioned strength or rise above the sanctioned strength by more than 10% of the sanctioned strength. Both instances of "strength" in this context refer to the total number of students in the class.
4.  Regardless of Rule 3, a minimum of one student from each discipline will be qualified to be considered for a change of branch at the end of the first year.
5. If a student with a higher GPA is denied access to a certain branch due to  

Other restrictions aside, this should not be made available to any other students with a lower GPA, even if they meet the requirements based on the standards in place.

B. Understanding the Rules of Branch Change

1. Sanctioned Strength

The sanctioned strength is the number of seats allowed to a specific branch. The Institute which we have taken for working  now has four branches, each with its own set of sanctioned strengths: Computer Science and Engineering (CSE) - 50,

Electrical Engineering (EE) - 50,

Mechanical Engineering (ME) - 40,

Civil Engineering (CE) - 40

2. Existing Strength

Existing Strength refers to the number of students who have joined a particular branch at the start of the first semester. Existing strength may differ from sanctioned strength since some seats may be unoccupied.

a. Rule 3 says that a class’s strength should not drop below its existing strength by more than 10% of the sanctioned strength. Let’s assume the existing strength of CSE is 47. As sanctioned strength as mentioned above is 50, 10% of 50 = 5. This means that the existing strength may only drop by 5 i.e, 42. This is referred to as being ”Floored out” or ”Bottomed out.”

b. Rule 3 says that a class’s strength should not exceed the sanctioned strength by more than 10%. Let’s assume the sanctioned strength for CSE is 50. 110% of 50 equals 55. As a result, the strength can reach a maximum of 55. This is referred to as being ”Roofed out” or ”Maxed out”.

c. Rule 4 is a sub-case of Rule To deal with situations like this, the term irrespective of rule 3 is used. For example, if a branch’s sanctioned strength is just 8 (any natural number less than 10 may be used as an example) then that branch’s existing strength will definitely be 8 or below, now 10% of the sanctioned strength is less than one, So branch can’t lose a student as the strength of a class will fall below the existing strength by more than ten percent of the sanctioned strength. As a result, Rule 4 assures that only one student can leave that branch under such circumstances.

3. Origin of Rule-5

The origin of Rule - 5 would have most likely been to guarantee that this reallocation was done fairly. Though this regulation appears to be fair for a student with a higher GPA, it may also be detrimental to a student with a higher GPA.

4. Supremum Criteria for Allocation

The student with the highest GPA is prioritized under this criterion. Assume there are two allocations, A1 and A2, that are sorted by GPAs in decreasing order. If student S gets his better preference in A1 over A2, we say A1 is optimal/better. Where S is the first student from the top whose allocation has been changed.

III. ALLOCATION VERIFIER APPROACH

After reviewing the prior works we began to see the problem in a new way. We wanted to verify if a given allocation is optimal or not. If the allocation is not optimal, we’ll need to figure out why (The thought behind this is if we figure out why our allocation isn’t optimal and then figure out how to solve it). By solving it we can get into a better/optimal allocation. Now, this problem can be seen as an Allocation Verifier.

A. Problem Statement

We will be given a particular allocation and we need to verify whether it is the optimal allocation (following the supremum criteria) for the given branch change requests.

1. We assume the given allocation is not optimal and we try to check whether our assumption is right or wrong .
2. In the given allocation the students will be in the order of decreasing GPA.
3. We will take the first student who did not get his first preference and we try to find a way that will improve his preference.
4. If we find a way to improve the preference for this student we can say that the given allocation is not optimal. If not we repeat this procedure for all the students below him.
5. If none of the students got into their better preferences then we can conclude that the given allocation is optimal.

There are just three reasons for a student for not getting the better preferences in the given allocation.

• The current branch of the student is floored out
• The preferred branch of the student is roofed out
• Or the allocation does not obey rule-5.

But for the first person who misses out on his first preference, let say S1, only the first 2 reasons (from above mentioned) will be applicable. If he misses out on any of the preferences then those particular branches cannot be allocated to any of the students below him by rule-5(As he is the person(S1) with the highest CGPA who got rejected for a branch that means that all the other students below him should also be rejected). Now we need not verify the branch request by other students for the branch the S1 got rejected. So we can decline/remove all the requests to that branch for all the students below him( this will eliminate all the rejections to that branch by rule-5) . The student immediately below S1, let’s say S2, there won’t be rule 5 into consideration and has only the possible floored out and roofed out reasons for rejection . So we can treat all the students below S1 the same way we treated S1.

B. Conclusion

We have to find out the different structures for both the scenarios (floored out and roofed out) in which we can tackle these cases.

We decided to put this Allocation Verifier approach on hold because we discovered a better analogy for the Branch Change Problem with Hospital-Residence Problem. So we went on to the research papers on it, and the literature review for those can be found in the following chapter.

IV. LITERATURE REVIEW

In Computer Science, the stable marriage problem (also known as the stable matching problem) is the problem of finding a stable matching equal-sized sets of elements given a preference ordering for each element.

The Hospitals/Residents problem is a many-to-one extension of the stable marriage problem. In this case, each hospital imposes a quota, or an upper limit on the number of seats it can provide. For this problem, there exists at least one stable matching, and finding one can be done in polynomial time. The papers which we will be looking below will study an extension of this problem in which each hospital sets not only an upper limit but also a lower limit on the number of seats. This problem is known as Hospital/Residence problem with Lower Quotas(HR-LQ). We’ll study some papers on HR-LQ because the problem is quite similar to our branch change problem. We can find a good analogy between these two problems: hospitals are branches, residents are students and as we are not allowed to go below the 10% of the existing strength this will be the lower quota. But the major difference is that we are already allocated into a branch and we need to relocate them whereas HR-LQ problem is for a new allocation (i.e, if we directly remodel this we’ll be allocating them from scratch so they might lose their current branch).

We’ll study the below mentioned research papers and try to adapt them to our problem or we will gain the knowledge which might be helpful to tackle the branch change problem.

A. Envy-Free Matchings with Lower Quotas by Yu Yokoi[1]

As mentioned above every HR instance has a stable matching but with the lower quotas we won’t have any stable matchings guaranteed. For such instances, by weakening the fairness properties we can expect an existence of an envy free matching.

They characterized the existence of an envy-free matching in the following way: Let I be a given HR-LQ instance, and I′ be the HR instance generated by eliminating lower quotas and replacing upper quotas with the original lower quotas from I. They showed that I has an envy-free matching if and only if every hospital in a stable matching of I′is full. Combining this characterisation with the Rural Hospital Theorem results in an efficient algorithm for determining the existence of an envy-free matching for an HR-LQ instance.

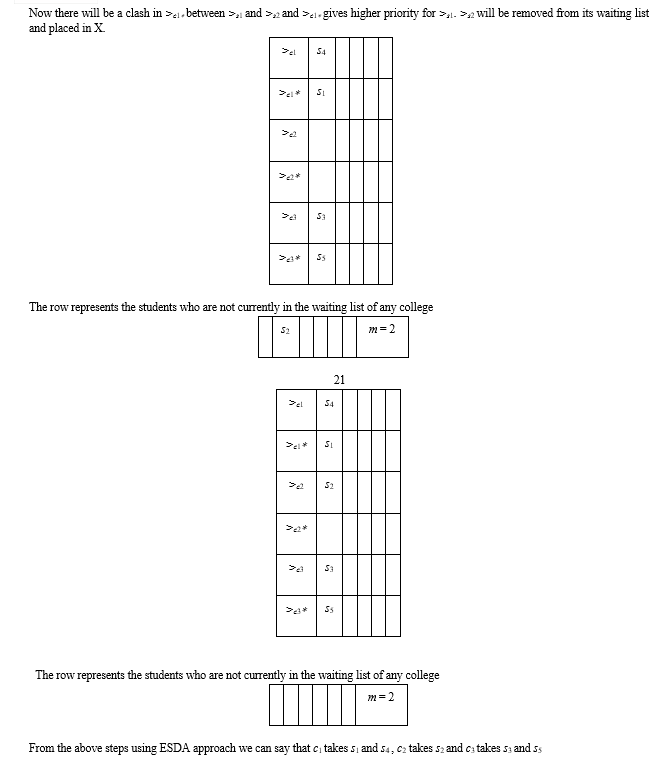
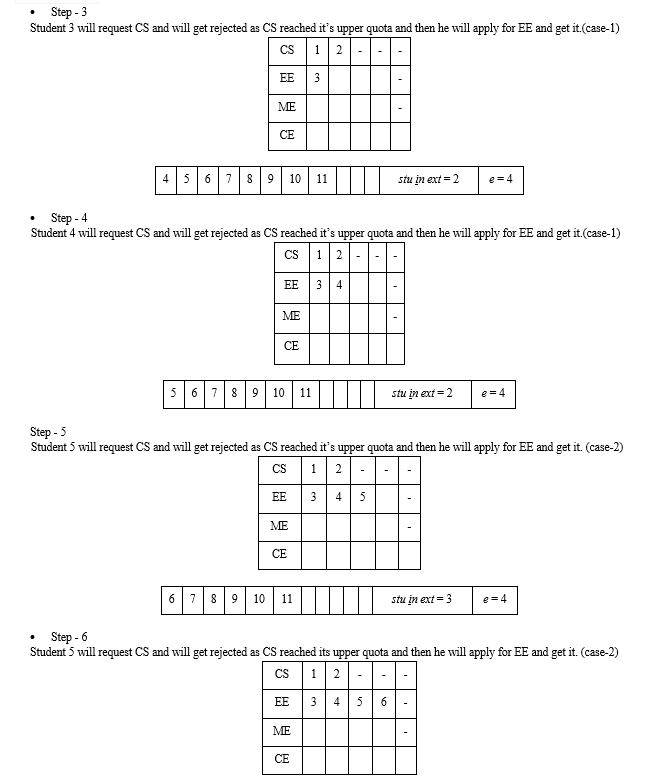
This allocation exactly matches with the allocation that the academic section has arrived at for this set of branch change requests. This algorithm takes less than a second for execution for this input, We also tested this for a random data with 4 branches and 1000 students it still takes less than a second for execution. Where as the brute force algorithm takes around 58 minutes for 4 branches and 20 students to arrive at the solution.

Conclusion

We have successfully designed a polynomial time algorithm for the Branch Change problem with supremum rule. Time complexity of our algorithm is O(b2s3log(s))) compared to exponential time (O(bs)) of the Brute force solution for the problem with only supremum rule. Where s is the number of students and b is the number of branches. In our code we are sorting the students of non home branches while allocating. By using priority queue instead of sorting there then we might improve our time complexity. We are yet to prove that the result we get using this algorithm is the optimal solution or not. If it isn\'t then how close it is to the optimal solution.

References

[1] Y. Yokoi, “Envy-free matchings with lower quotas,” 2018. [2] D. FRAGIADAKIS, A. IWASAKI, P. TROYAN, S. UEDA, and M. YOKOO, “Strate gyproof matching with minimum quotas,” 2015. [3] Branch Change Rules, IIT Palakkad. [Online]. Available: https://drive.google.com/ file/d/1VulhJ0R7LsTVPBclxvd8gllMddTTl4Rk/view [4] Kasireddy Durga Prasad Reddy, “Graph theoretic approach on branch reallocation,” B.Tech Project Report, Computer Science and Engineering, IIT Palakkad, 2019. [5] Vishnu Teja, “Graph theoretic approach on branch change,” B.Tech Project Report, Computer Science and Engineering, IIT Palakkad, 2020.

Copyright

Copyright © 2023 Jemunigani Jishnu, Juttu Gajendra Anurag, Eturu Harshith. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.