Design and Performance Evaluation of Brent Kung Adder based 8-Bit Vedic Multiplier

Abstract

Multiplier is an essential functional block of a microprocessor because multiplication is needed to be performed repeatedly in almost all scientific calculations. Therefore, design of fast and low power binary multiplier is very important particularly for Digital Signal Processors. Vedic mathematics has improved the performance of multiplier. Vedic mathematics, a system of ancient Indian mathematics, which has a unique technique of solutions based on only 16 sutras. The novel point is the efficient use of Vedic algorithm (sutras) that reduces the number of computational steps considerably compared with any conventional method. This paper presents design and Performance Evaluation of Brent Kung Adder based 8-Bit Vedic Multiplier. Urdhva Tiryagbhyam sutra has been used for multiplication purpose. The partial product addition in Vedic multiplier is realized using Brent Kung Adder. Simulation results shows that described Brent Kung Adder based 8-Bit Vedic Multiplier is efficiently decreases the Delay, power consumption and Area than other multipliers.

Introduction

I. INTRODUCTION

In most of the digital systems, multiplier and adder are the fundamental components in the design of application specific integrated circuits like RISC processors, digital signal processors (DSP), microprocessors etc. Now a day’s high speed devices play key role in VLSI applications. So the designing of fast devices has become essential to fulfill the demand of end user [1]. For multiplication operation performed in DSP applications, latency and throughput are the two major concerns from delay perspective.

The speed of processor depends on the performance of Multiplier. A logic circuit which is combinational in nature and employed in a digital circuits to perform the multiplication operation can be called a multiplier. In past decade several new Architecture of Multiplier has been design like Booth’s multiplier, Modified Booth multiplier [2], Wallace Multiplier etc. In these algorithms various partial products are generated and also runs through various steps to attain the final resultant. The various steps comprises of addition, subtraction, and many comparisons which as a result consume much time therefore reduce the speed of multiplier. Since speed is major concern for Multiplier Design, therefore these architectures are not feasible [3].

Vedic multiplication is considered as the oldest Indian ancient technique which is successfully used in designing multilevel 2d-DWT and image processing [4]. Designing of these systems involve careful analysis of multiplication algorithms. Some of the important factors based on which the performance of a multiplier is judged are area, speed and power consumption. In recent time, a number of research articles have been published to reduce the computational complexity of the multiplication algorithm.

Vedic mathematics was reconstructed from the ancient Indian scriptures (Vedas) by Swami Bharati Krishna Tirthaji Maharaja (1884-1960) after his eight years of research on Vedas. Vedic mathematics is mainly based on sixteen principles or word-formulae which are termed as sutras [5]]. This is a very interesting field and presents some effective algorithms which can be applied to various branches of engineering such as computing and digital signal processing. Integrating multiplication with Vedic Mathematics techniques would result in the saving of computational time. Thus, integrating Vedic mathematics for the multiplier design will enhance the speed of multiplication operation. The multiplier architecture is based on Urdhva Tiryagbhyam (vertical and cross-wise algorithm) sutra. An illustration of Urdhva Tiryagbhyam sutra is shown in Figure 1.

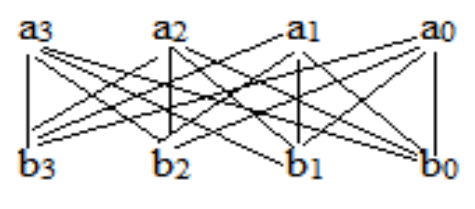
Figure 1. Illustration of Urdhva Tiryagbhyam sutra

The 4x4 multiplication has been done in a single line in Urdhva Tiryagbhyam sutra, whereas in shift and add (conventional) method, four partial products have to be added to get the result. Thus, by using Urdhva Tiryagbhyam Sutra in binary multiplication, the number of steps required calculating the final product will be reduced and hence there is a reduction in computational time and increase in speed of the multiplier.

This paper presents Design and Performance Evaluation of Brent Kung Adder based 8-Bit Vedic Multiplier.  Urdhva Tiryagbhyam sutra has been used for multiplication purpose.  The partial product addition in Vedic multiplier is realized using Brent Kung Adder.

Remaining paper is organized as follows: Section II presents literature survey, Section III presents described Brent Kung Adder based 8-Bit Vedic Multiplier. Section IV presents simulation results and performance analysis of described multiplier, finally paper is concluded with section V.

II. LITERATURE SURVEY

In [6], a high speed multiplier is proposed using Urdhva Tiryagbhyam sutra and MUX based adder. The Experimental results shows that the proposed multiplier with MUX based adder can achieve significant improvement in speed and area.

In [7] describes another new architecture of Vedic multiplier which is the combination of Urdhva Tiryagbhyam sutra of Vedic maths for performing high speed multiplication and kogge stone algorithm for adding partial products. Kogge stone adder is a parallel prefix adder. The Verilog code of 8x8 proposed multiplier was synthesized using Xilinx ISE 9.1i. It is found that the proposed architecture reduces the delay.

In [8], two possible architectures are proposed for a Vedic real multiplier based on the URDHVA TIRYAKBHYAM (Vertically and cross wise) sutra of Indian Vedic mathematics and an expression for path delay of an N×N Vedic real multiplier with minimum path delay architecture is developed. Then, architectures of four Vedic real multipliers solution, three Vedic real multipliers solution of complex multiplier are presented. Finally, the results are compared with that of the four and three real multipliers solutions using the conventional Booth and Array multipliers.

In [9] design a Vedic multiplication algorithm by using Vedic mathematics formula Urdhava Tiryakbhyam method means vertically and cross wise. The speed of the computation process is increased and the processing time is reduced due to decrease of combinational path delay compared to the existing multipliers. In our proposed multiplication algorithm, we get less time delay compared to other algorithms.

In [10] presents the HDL implementation of a novel multiplier algorithm based on the combination of Vedic mathematics and Booth-Wallace tree multiplier. An 8×8 multiplier is implemented in VHDL. The HDL code is simulated and synthesized using ModelSim and Xilinx ISE 14.1, respectively. The performance parameters of 8-bit multipliers implemented using various algorithms are compared in this paper. The comparison results exhibit that the proposed algorithm is faster than other multiplier algorithms.

In [11] proposed multiplier pertaining to concepts of Vedic Mathematics was designed to reduce propagation delay, design complexity as well as to optimize power consumption in comparison to conventional multipliers. The Vedic Multiplier computed the partial products in a simultaneous manner and the carry was propagated using ripple carry adders. Upon simulation of the results, the Vedic Multiplier was found to restrict the delay, compared to the Array and Booth Multipliers.

In [12] proposed multiplier architectures are based on the Urdhva and Nikhilam sutras of the Vedic Mathematics. The Urdhva multiplier generates the partial products and the sums in parallel. Hence, this multiplier reduces the carry propagation delay from LSB to MSB.  The proposed Urdhva and Nikhilam multipliers achieve 60%, 77% improvement in speed and 37%, 50% improvement in power respectively, as compared with the power consumption of the conventional array multipliers.

III. BRENT KUNG ADDER BASED 8-BIT VEDIC MULTIPLIER

In this paper, Design and Performance Evaluation of Brent Kung Adder based 8-Bit Vedic Multiplier is presented.

A. Brent–Kung Adder

A Brent–Kung adder is a high-speed parallel prefix adder that uses a tree structure to perform arithmetic operations. It was developed by Brent and Kung. PPA is the unique architecture of adders that uses generate and propagate signals. BKA takes less area than other PPAs. Less cost and wiring congestion are other advantages of Brent Kung adder. It will increase the speed of partial product addition without compromising the power performance of the adder. It gives minimal number of calculating nodes but it has maximum logic depth and minimum area. Brent Kung adder has 3 stages namely pre-processing stage, prefix carry tree stage and post-processing stage.

Preprocessing: - This progression includes calculation of create and spread signs comparing too each combine of bits in An and B. These signs are given by the rationale conditions beneath:

Pi=Ai XOR Bi…(1)

Gi=Ai AND Bi…(2)

Carry look ahead network: - This square separates KSA from different adders and is the primary power behind its superior. This progression includes calculation of conveys comparing to each piece.

Ci=Gior Pi and Ci-1…..(3)

Post processing: - This is the last advance and is normal to all adders of this family (convey look forward). It includes calculation of total bits. Total bits are figured by the rationale given underneath:

Si=Pi XOR Ci-1…..(4)

B. 8-bit Vedic multiplier using Brent–Kung adder

The 8-bit multiplier is designed using four 4x4 Vedic multipliers which employ Urdhva Tiryagbhyam sutra and Brent–Kung adder technique for partial product addition. 2 x 2 Vedic multiplier is used as a basic building block for design of 4 x 4 bit Vedic multiplier. The output of these Vedic multipliers is added by modifying the logic levels of Brent–Kung adder. Block diagram of the proposed 8x8 multiplier is illustrated in Figure 2.

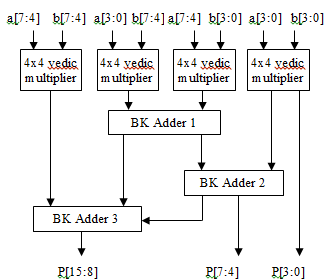
Figure. 2. Block diagram of Brent Kung Adder based 8-Bit Vedic Multiplier

The 8-bit input sequence is divided into two 4-bit numbers and given as inputs to the 4-bit multiplier blocks (a[7:4] & b[7:4], a[3:0] & b[7:4], a[7:4] & b[3:0], a[3:0] & b[3:0]). The four multipliers used are similar and give 8-bit intermediate products which are added using overlapping logic with the help of three Brent–Kung (BK) adders. The partial products obtained from the four multipliers are demarcated into four regions.

The four LSB product bits P[3:0] are directly obtained from one of the multipliers. The output of the second and third multiplier block is added directly using BK adder -1 as the second and third region is overlapping. Then the higher order bit of first multiplier block is added to the overlapping sum using BK adder-2 which gives the product P[7:4]. Finally, MSB bits P[15:8] are obtained by adding the fourth multiplier output to the carry from BK adder -1 (added at the fifth bit position) and higher order bits (acts as lower nibble of addend) of BK adder -3.

IV. RESULT ANALYSIS

Implementation details and performance analysis of described Design and Performance Evaluation of Brent Kung Adder based 8-Bit Vedic Multiplier is analyzed in this section. Xilinx 14.7 has been used for synthesize the Verilog codes of multipliers. Delay, power consumption and Area are three important parameters used in this paper to evaluate the performance analysis. The RTL schematic of described Brent Kung Adder based Vedic Multiplier is shown n below Figure 3.

Figure. 3. RTL schematic of Brent Kung Adder based 8-Bit Vedic Multiplier

Below Table 1 shows the comparative analysis of described Brent Kung Adder based 8-Bit Vedic Multiplier, Vedic Multiplier using MUX based adder and Vedic Multiplier using Ripple Carry adder in terms of delay, power consumption and Area.

Table. 1. Comparative performance analysis

Figure 4 shows the comparative graphical analysis of delay parameter for Vedic Multiplier using described Brent Kung Adder, MUX based adder and Ripple Carry adder. It is observed that, described Brent Kung Adder based 8-Bit Vedic Multiplier is achieves less delay compared to other multipliers.

Figure 4. Comparative analysis for Delay parameter

Comparative graphical analysis of power consumption parameter for Vedic Multiplier using described Brent Kung Adder, MUX based adder and Ripple Carry adder is shown in below Figure 5 and results clears that less power consumption attained by described model.

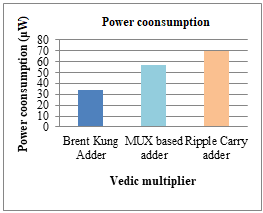
Figure 5. Comparative analysis for power consumption

Vedic Multiplier using described Brent Kung Adder, MUX based adder and Ripple Carry adder comparative area (number of LUTs) is graphically represented in below Figure 6. Described model multiplier has less area has other multipliers.

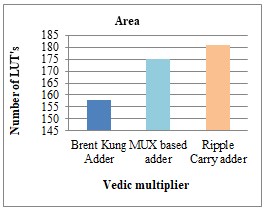
Figure 6. Comparative analysis for Area

From overall result analysis it is observed that, described Vedic Multiplier using described Brent Kung Adder gives a superior performance as compared with other multipliers.

Conclusion

In this paper, Design and Performance Evaluation of Brent Kung Adder based 8-Bit Vedic Multiplier is presented. Multipliers assume an essential part in the present advanced flag handling and different applications. Integrating Vedic mathematics for the multiplier design will enhance the speed of multiplication operation. The 8-bit multiplier is designed using four 4x4 Vedic multipliers which employ Urdhva Tiryagbhyam sutra and Brent–Kung adder technique for partial product addition. Delay, power consumption and Area are three important parameters used in this paper to evaluate the performance analysis. From overall result analysis it is observed that, described Vedic Multiplier using described Brent Kung Adder gives a superior performance as compared with other multipliers.

References

[1] J. Sommer, M. A. Özkan, O. Keszocze and J. Teich, \"DSP-Packing: Squeezing Low-precision Arithmetic into FPGA DSP Blocks,\" 2022 32nd International Conference on Field-Programmable Logic and Applications (FPL), Belfast, United Kingdom, 2022, pp. 160-166, doi: 10.1109/FPL57034.2022.00035. [2] S. Rooban, M. Nagesh, M. V. S. L. Prasanna, K. Rayudu and G. D. Sai, \"Implementation of 128-bit Radix-4 Booth Multiplier,\" 2021 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 2021, pp. 1-7, doi: 10.1109/ICCCI50826.2021.9457004. [3] F. G. Dell\'Anna, T. Dong, P. Li, W. Yumei, M. Azadmehr and Y. Berg, \"Low-power voltage multiplier synthesis tool for preliminary topology identification,\" 2017 International Conference on Open Source Systems & Technologies (ICOSST), Lahore, Pakistan, 2017, pp. 24-29, doi: 10.1109/ICOSST.2017.8279000. [4] L. Mandal and K. Dasgupta, \"Use of Vedic Mathematics to Speed-up Basic Mathematical Operations in Android Based Calculator,\" 2019 International Conference on Intelligent Sustainable Systems (ICISS), Palladam, India, 2019, pp. 162-165, doi: 10.1109/ISS1.2019.8907961 [5] S. Akhter and S. Chaturvedi, \"Modified Binary Multiplier Circuit Based on Vedic Mathematics,\" 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 2019, pp. 234-237, doi: 10.1109/SPIN.2019.8711583. [6] Saji. M. Antony , S.Sri Ranjani Prasanthi, Dr.S.Indu, Dr. Rajeshwari Pandey , (2015) Design of High Speed Vedic Multiplier using Multiplexer based Adder 2015 International Conference on Control, Communication & Computing India (ICCC) 19-21,IEEE. [7] Sudeep.M.Cs, Sharath Bimba.M, Mahendra Vucha, (2014) Design and FPGA Implementation of High Speed Vedic MultiplierInternational Journal of Computer Applications Volume 90, [8] K. D. Rao, C. Gangadhar and P. K. Korrai, \"FPGA implementation of complex multiplier using minimum delay Vedic real multiplier architecture,\" 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON), Varanasi, India, 2016, pp. 580-584, doi: 10.1109/UPCON.2016.7894719. [9] D. K. Kahar and H. Mehta, \"High speed vedic multiplier used vedic mathematics,\" 2017 International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 2017, pp. 356-359, doi: 10.1109/ICCONS.2017.8250742. [10] A. Jain, S. Bansal, S. Khan, S. Akhter and S. Chaturvedi, \"Implementation of an Efficient N× N Multiplier Based on Vedic Mathematics and Booth-Wallace Tree Multiplier,\" 2019 International Conference on Power Electronics, Control and Automation (ICPECA), New Delhi, India, 2019, pp. 1-5, doi: 10.1109/ICPECA47973.2019.8975673. [11] V. Meghana, Sandhya S, Aparna R and C. Gururaj, \"High speed multiplier implementation based on Vedic Mathematics,\" 2015 International Conference on Smart Sensors and Systems (IC-SSS), Bangalore, India, 2015, pp. 1-5, doi: 10.1109/SMARTSENS.2015.7873593. [12] S. Patil, D. V. Manjunatha and D. Kiran, \"Design of speed and power efficient multipliers using vedic mathematics with VLSI implementation,\" 2014 International Conference on Advances in Electronics Computers and Communications, Bangalore, India, 2014, pp. 1-6, doi: 10.1109/ICAECC.2014.7002484.

Copyright

Copyright © 2024 Maznu Shaik, B Ramakrishna, B. Ashok, K Rajesh Kumar, Rajashekhar K. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.