Case Study on Breast Cancer Detection using K-Nearest Neighbour Algorithm

Abstract

Breast cancer is one of the common occurring cancer in women across the globe, affecting about significant percentage of women at some point in their life. Even with the development of new technologies in the field of medicine and research, the accurate diagnosis of this fatal disease outcome is one of the most important tasks needed to be done till date. Our objective is to develop a sophisticated and automated diagnostic system that yields accurate and reproducible results for predicting whether a breast cancer tumour is benign (non-cancerous) or malignant (cancerous). We have implemented KNearest Neighbour Algorithm using various normalization techniques and distance functions at different values of K. A comparative study using various distance metrics, i.e., Euclidean distance, Pythagorean distance has been done. The accuracy of each variation is tested and the maximum accurate prediction is considered for the result. Highest accuracy of 121/143 = 84.6% is achieved, with KNN implementation using Euclidean distance metric at k=5.

Introduction

I. INTRODUCTION

Breast cancer is the second most common type of cancer in women and one of the leading causes of cancer related deaths. As per statistics (Berry, 2017),the breast cancer occurs more in western countries when compared to developing countries. On the contrary, the death rates due to breast cancer, from the developing countries, disease are higher as compared to the death rates, due to the same, from developed countries. It also states that the rate of breast cancer per 100,000 women is higher in the U.S., Canada, and Europe.

Breast cancer occurs when an infected tissue (tumour) begins to spread quickly. These cancerous cells can move anywhere within the body causing further damage.

There are two types of breast cancer tumours:

1. Non-cancerous or ‘benign’
2. Cancerous or ‘malignant’

Timely prediction requires a precise and authentic methodology to distinguish between benign breast tumors from malignant ones. Nowadays, diagnostic tests such as Surgical Biopsy have been replaced by Fine Needle Aspiration (FNA).

However, the accurate prediction of fatal disease outcome is still one of the most challenging tasks needed to be done till date and various Machine Learning techniques have become a popular tool to resolve this problem. Machine learning predictive analytics and pattern recognition have achieved 89% accuracy rate (Yun Liu, 2017). That’s quite a bit ahead of an average score of 73% for the existing system of surgical biopsy. Also, using machine learning techniques, there is relative reduction in cost as less human effort is required. Furthermore, the fast speed at which machine learning consumes data allows the system to produce real-time data and predictions in a shorter duration of time.

II. RELATED WORK

An easy way to comply with IJRASET paper formatting requirements is to use this document as a template and simply type your text into it.

Authors in (Shagun Chawla, Rajat Kumar, 2018), implemented KNearest Neighbour Algorithm using various normalization techniques and distance functions at different values of K. A comparative study using various normalization techniques, i.e., Min-Max normalization, Z-Score normalization and Decimal Scaling normalization, and different distance metrics, i.e., Manhattan distance, Euclidean distance, Chebyshev distance and Cosine distance has been done. The accuracy of each variation is tested and the maximum accurate prediction is considered for the result. Highest accuracy of 98.24% is achieved, with KNN implementation using Manhattan distance metric, at K=14, along with Decimal scale normalization.

Authors in (Seyyid Ahmed Medjahed, 2013), compared the accuracy of k-NN using several distances and different normalization techniques. Various distances included were Euclidean distance, City Block Distance, Cosine distance and Correlation distance. The k-parameter in the algorithm had a range from 1 to 50. Highest accuracy of 98.70% was obtained when the kparameter was taken as 1 and Euclidean distance was chosen as the distance metric.

The accuracy of Naïve Bayes, SVM and Ensemble Algorithm were analyzed by Animesh et. al. in (Hazra, Mandal & Gupta, 2016). Using feature selection, it was found that Naïve Bayes gave maximum accuracy of 97.3978% by selecting only 5 dominant features.

In (Janghel, 2010), authors’ implemented four models of neural networks namely Back Propagation Algorithm, Radial Basis Function Networks, Learning vector Quantization and Competitive Learning Network. In the best configuration, it was observed that Learning Vector Quantization, Competitive Learning and Multi-Layer Perceptron algorithms had testing accuracy of 95.82, 74.48 and 51.88% respectively.

In (Hiba, Hajar & Hassan, 2016), Hiba Asri, HajarMousannif, Hassan Al Moatassime and Thomas Noel have compared efficiencies among Support Vector Machine (SVM), Naïve Bayes (NB) and k Nearest Neighbours (k-NN) on the breast cancer data set with accuracy of 97.13, 95.99and 95.27 respectively.

Othman and Thomashave analyzed the breast cancer dataset using WEKA in (Bin & Yau, 2017), by applying Bayes Network, Radial BasisFunction, Pruned Tree, Single Conjunctive Rule Learner and Nearest Neighbour Algorithm. The highest accuracy of 89.71% was achieved by Naïve Bayes algorithm followed by Radial Basis Function with an accuracy of 87.43%. while the Nearest neighbours algorithm achieved the accuracy of 84.57%.

In (Rana, 2015) Mandeep Rana et. al. compared the accuracy of Support Vector Machine, Logistic Regression, KNN and Naive Bayes. It was observed that the highest testing accuracy of 95.68% was achieved by k-NN with Euclidean distance.

Above discussed work had taken the Wisconsin Breast Cancer Dataset (Street, Wolberg, Mangasarian & Goldgof, 1993) for the reference.

III. EXPERIMENT AND METHODOLOGY

The various materials that have been used in the paper include: Python for coding purposes and Breast Cancer Dataset. The technique used is K-Nearest Neighbour.

A. K-Nearest Neighbour (K-NN)

K-Nearest Neighbors, or KNN for short, is one of the simplest machine learning algorithms and is used in a wide array of institutions. KNN is a non-parametric, lazy learning algorithm. When we say a technique is non-parametric, it means that it does not make any assumptions about the underlying data. In other words, it makes its selection based on proximity to other data points regardless of what feature the numerical values represent. 

Being a lazy learning algorithm implies that there is little to no training phase. Therefore, we can immediately classify new data points as they present themselves.

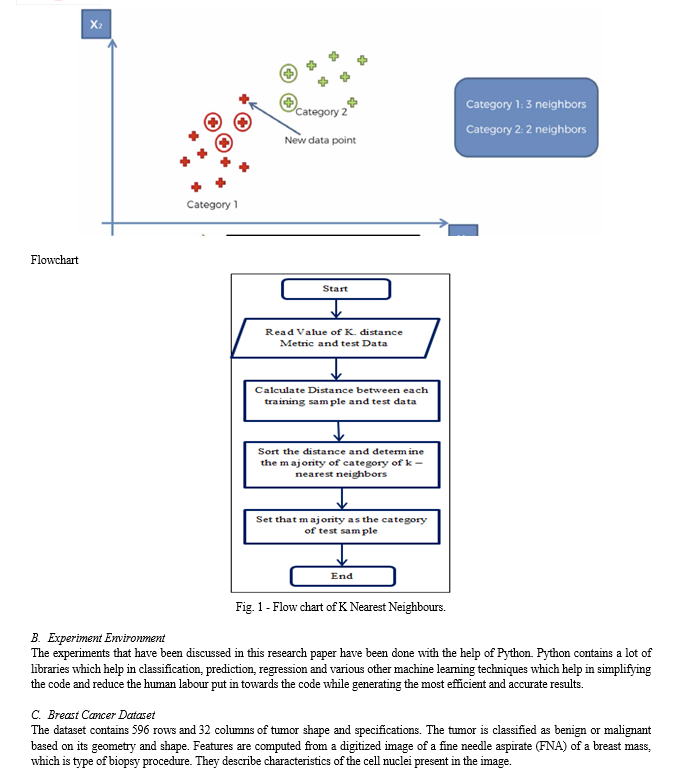
The features of the dataset include:

1. tumor radius (mean of distances from center to points on the perimeter)
2. texture (standard deviation of gray-scale values)
3. perimeter
4. area
5. smoothness (local variation in radius lengths)
6. compactness (perimeter² / area — 1.0)
7. concavity (severity of concave portions of the contour)
8. concave points (number of concave portions of the contour)
9. symmetry
10. fractal dimension

The mean, standard error and “worst” or largest (mean of the three largest values) of these features were computed for each image, resulting in 30 features.

IV. CODE AND RESULT

Let’s take a look at how we could go about classifying data using the K-Nearest Neighbors algorithm in Python. For this case study, we’ll be using the breast cancer dataset from the sklearn.datasets module. We need to start by importing the proceeding libraries.

import numpy as np

import pandas as pd

from matplotlib import pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.metrics import confusion_matrix

from sklearn.neighbors import KNeighborsClassifier

from sklearn.model_selection import train_test_split

import seaborn as sns

sns.set()

#We can set the style by calling Seaborn's set() method

The dataset classifies tumors into two categories (malignant and benign) and contains something like 30 features. In the real world, you’d look at the correlations and select a subset of features that plays the greatest role in determining whether a tumor is malignant or not. However, for the sake of simplicity, we’ll pick a couple at random. We must encode categorical data for it to be interpreted by the model (i.e. malignant = 0 and benign = 1).

breast_cancer = load_breast_cancer()

X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)

X = X[['mean area', 'mean compactness']]

y = pd.Categorical.from_codes(breast_cancer.target, breast_cancer.target_names)

y = pd.get_dummies(y, drop_first=True)

#Make a Categorical type from codes and categories or dtype. This constructor #is useful if you already have codes and categories/dtype and so do not need #the factorization step

As mentioned earlier, the point of building a model, is to classify new data with undefined labels. Therefore, we need to put aside data to verify whether our model does a good job at classifying the data. By default, train_test_split sets aside 25% of the samples in the original dataset for testing.

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

The sklearn library has provided a layer of abstraction on top of Python. Therefore, in order to make use of the KNN algorithm, it’s sufficient to create an instance of KNeighborsClassifier. By default, the KNeighborsClassifier looks for the 5 nearest neighbors. We must explicitly tell the classifier to use Euclidean distance for determining the proximity between neighboring points.

knn = KNeighborsClassifier(n_neighbors=5, metric='euclidean')

knn.fit(X_train, y_train)

Using our newly trained model, we predict whether a tumor is benign or not given its mean compactness and area.

y_pred = knn.predict(X_test)

We visually compare the predictions made by our model with the samples inside the testing set.

???????

Conclusion

The K Nearest Neighbors algorithm doesn’t require any additional training when new data becomes available. Rather it determines the K closest points according to some distance metric (the samples must reside in memory). Then, it looks at the target label for each of the neighbors and places the new found data point into the same category as the majority. Given that KNN computes distance, it’s imperative that we scale our data. In addition, since KNN disregards the underlying features, it’s our responsibility to filter out any features that are deemed irrelevant.

References

[1] Shagun Chawla ,Rajat Kumar,Eknath Aggrarwal,Sarthak Swain,”Breast Cancer Detection Using K-Nearest Neighbour Algorithn”,in International Conference on Computational Intelligence and Internet of Things,2018. [2] Berry, J. (2017, April 26). \"Worldwide statistics on breast cancer: Diagnosis and risk factors.\" Medical News Today. Retrieved from https://www.medicalnewstoday.com/articles/317135.php. [3] Yun Liu et al., Detecting Cancer Metastases on Gigapixel Pathology Images”,2017. Available:arXiv:1703.02442 [4] Seyyid Ahmed Medjahed et al.,”Breast Cancer Diagnosis by using k-Nearest Neighbor with Different Distances and Classification Rules”, in International Journal of Computer Applications (0975 - 8887), Vol. 62-No.1,January 2013. [5] Hazra Animesh, Mandal K. Subrata and Gupta Amit, “Study and Analysis of Breast Cancer Cell Detection using Naïve Bayes, SVM and Ensemble Algorithms.\" International Journal of Computer Applications 145(2):39-45, July 2016. [6] R.R.Janghel et al.,“Breast cancer diagnosis using Artificial Neural Network models”, IEEE , August 2010. [7] Hiba Asri, Hajar Mousannif, Hassan Al Moatassime, Thomas Noel, “Using Machine Learning Algorithms for Breast Cancer Risk Prediction and Diagnosis”, Elsevier, 2016, DOI 10.1016/j.procs.2016.04.224, [8] Bin Othman M.F., Yau T.M.S. (2007),“Comparison of Different Classification Techniques Using WEKA for Breast Cancer.” In: Ibrahim F., Osman N.A.A.,Usman J., Kadri N.A. (eds) 3rd Kuala Lumpur International Conference on Biomedical Engineering 2006. IFMBE Proceedings, vol 15. Springer, Berlin, Heidelberg. [9] Rana, Mandeep, “Breast Cancer Diagnosis And Recurrence Prediction Using Machine Learning Techniques.” International Journal of Research in Engineering and Technology, 2015. [10] Hamou, Reda Mohamed. \"Handbook of Research on Biomimicry in Information Retrieval and Knowledge Management.\" IGI Global, 2018. 1-429. Web. 11 Mar. 2018. [11] Mandelbrot, B.B. (1977), The Fractal Geometry of Nature, W.H. Freeman and Company, New York. Dodge Y, ”The Oxford Dictionary of Statistical Terms”,(2003) [12] N. Katayama and S. Satoh, \"Distinctiveness-sensitive nearest-neighbor search for efficient similarity retrieval of multimedia information,\"Proceedings 17th International Conference on Data Engineering, Heidelberg, 2001, pp. 493-502. [13] Anton, Howard (1994), “Elementary Linear Algebra” (7th ed.), John Wiley & Sons, pp. 170–171, ISBN 978-0-471-58742-2 Deza, Elena; Deza, Michel Marie, “Encyclopedia of Distances”,(2009) Springer.p. 94. [14] Paul E. Black, \"Manhattan distance\", in Dictionary of Algorithms and Data Structures [online], Vreda Pieterse and Paul E. Black, eds. 31 May 2006. [15] Eugene F. Krause, “Taxicab Geometry”,(1987) Dover. [16] Cyrus. D. Cantrel, ”Modern Mathematical Methods for Physicists and Engineers” (2000), Cambridge University Press.

Copyright

Copyright © 2023 Chetana B. Bhagat, Udhav M. Parbhane. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.