Structural Analysis of Castellated Beams with Web Openings of Different Forms using Finite Element Method

Abstract

Castellated beams are increasingly important in modern structural engineering due to their enhanced strength-to-weight ratio, material efficiency, and versatility in various applications. These beams, formed by cutting and reassembling standard I-beams, offer significant advantages in reducing weight while maintaining or improving structural capacity. The present research focuses on the analysis of castellated beams using Finite Element Method (FEM) software to evaluate their behavior under various loading conditions. The study employs FEM to model these beams, simulating stress distribution, deformation, and failure modes across different configurations and loading scenarios. Factors such as span length, load type, and geometric variations are considered to assess their influence on performance. The findings provide valuable insights into the optimal design and application of castellated beams, contributing to the development of lightweight, strong structures in modern construction and supporting the advancement of sustainable engineering practices.

Introduction

I. INTRODUCTION

Castellated beams are frequently used in structural engineering because of their remarkable strength-to-weight ratio, efficient use of materials, and ability to span wide areas. They are distinguished by their distinctive "honeycomb" web pattern. To make these beams, an I-beam is cut along its web, and the fragments are then put back together to form a hexagonal or castellated design [1]. Castellated beams are a preferred choice in commercial and industrial building because of its unique structure's many advantages in terms of mechanical performance and material efficiency, especially in situations where large spans and low weight are essential. However, in spite of the significant benefits these beams offer, their complex shape and design make it difficult to predict their performance and design, highlighting the need for careful study [2].

 Given the numerous variables that affect castellated beam performance under load, including shear, bending, and torsional effects—all of which are often more complex than those in traditional solid beams—an analysis of these beams is essential. The web's perforations help to reduce weight and material costs, but they can also change the distribution of stress, which can change how the beam behaves under different loading conditions [3]. The consequences of these alterations could not be fully understood if they are not carefully examined, which might lead to ineffective designs or even structural failures. Thus, a thorough comprehension of castellated beams' mechanical behavior is essential to guaranteeing the dependability, safety, and economy of buildings that use them. The variety of elements influencing castellated beam performance is one of the primary justifications for the need to analyse them [4]. The arrangement of the web holes affects the beam's shear capacity, buckling resistance, vibration behavior, and stiffness and strength. A more complete investigation is required because the intricate stress distributions in castellated beams may cause localized failures that are difficult to detect in traditional beam analysis. Additionally, the re-welding process during manufacturing can introduce potential weak areas and residual stresses that may significantly modify the beam's load-carrying capability. Therefore, comprehending these factors through comprehensive analysis is essential for achieving optimal designs that prioritize both safety and cost-effectiveness [5]. The extensive range of applications for castellated beams is a major element emphasizing the need for analysis. These beams are commonly used in large-scale constructions where structural integrity is essential, such as skyscrapers, bridges, and warehouses. They are ideal for such activities because of their capacity to sustain heavy weights while using little material. Nevertheless, every project has distinct load requirements, span dimensions, and environmental variables that can influence the performance of the beams [6]. Consequently, detailed analysis is essential to customize the design of castellated beams according to the specific demands of each project, guaranteeing that the beams function as intended under different conditions.

As a result of their complex behavior, unique form, and wide range of applications, castellated beams require careful analysis. In order to maximize these beams' benefits and minimize any potential disadvantages, adequate analysis ensures that they are constructed and used efficiently [7]. By learning more about the mechanical performance of castellated beams, engineers may improve safety, reduce material costs, and improve their designs, making them a reliable and cost-effective choice in modern structural design [8].

II. ANALYSIS OF CASTELLATED BEAMS

The analysis of castellated beams using the Finite Element Method (FEM) has become a crucial technique for comprehending their structural behavior under various loading conditions. FEM is a computational method that allows engineers to model intricate shapes, such as the perforated web of castellated beams, and effectively predict their performance. By segmenting the beam into smaller, easier-to-manage elements, FEM can accurately capture the complex interactions within the beam and estimate its response to different stresses, deformations, and load distributions. For castellated beams, FEM enables a thorough evaluation of key elements like stress concentration, bending, shear forces, and overall structural stability [9]. It assists engineers in analysing the effects of different design variables, such as the size and arrangement of web openings, beam span, and material properties. This numerical approach is especially useful for optimizing beam design, as it reveals potential weaknesses and failure modes that traditional analytical methods might overlook. FEM analysis also allows for comparisons among various castellated beam designs and loading scenarios, helping to identify the most suitable design for specific applications [10]. By incorporating FEM into the design workflow, engineers can ensure that castellated beams meet safety standards, optimize material use, and improve their operational effectiveness. The research on castellated beams through FEM software has emerged as an important aspect of understanding their structural capabilities. Numerous studies have utilized FEM to evaluate parameters such as load-bearing capacity, deflection, and stress distribution, providing valuable insights into how these beams act under different loading conditions. Castellated beams exhibit enhanced load-carrying capability due to their greater moment of inertia. Research indicates that converting standard IWF beams into castellated forms can result in a capacity increase of 16.14%. The ultimate load-bearing capacity is influenced by the shapes of the web openings, with irregular openings behaving differently compared to regular ones. The presence of openings in castellated beams reduces shear rigidity, leading to increased deflections [11].

FEM analysis has demonstrated a strong correlation with experimental findings for various opening geometries. A generalized analytical formula has been developed to evaluate deflections in simply supported beams with different perforations. Studies conducted with FEM have revealed that the distribution of stress varies significantly around the openings under various loading scenarios [12]. The maximum equivalent von Mises stresses are influenced by the bending moments acting on the beam. The empirical formulas derived from FEM analyses provide a reliable method for estimating stress concentrations in castellated beams. Although FEM software like ABAQUS, ANSYS, and MIDAS FEA NX has been effective for the analysis of castellated beams, it is crucial to recognize the limitations of numerical models, such as the assumptions related to material behavior and boundary conditions, which may affect the accuracy of the results [13]. The study of castellated beams has attracted considerable interest due to their benefits, including reduced weight and less material consumption. Although they provide advantages in structural efficiency, there are still difficulties in accurately predicting their performance, especially regarding shear strength and stability under dynamic loads [14]. Current research is focused on exploring optimization strategies, emphasizing the enhancement of analytical models and the integration of experimental validation [15]. Anticipated advancements are likely to further enhance design practices, positioning castellated beams as a more efficient and adaptable choice in structural engineering. This research aims to analyse the behavior of castellated beams with various web opening shapes using finite element analysis through modelling in ABAQUS software.

III. ABAQUS SOFTWARE

A. History

ABAQUS was initially created in 1978 by Dr. David H. ABAQUS, a professor at MIT, as a finite element analysis (FEA) tool aimed at resolving intricate solid mechanics issues. The software was intended to tackle non-linear behavior, significant deformations, and complex material models that previous FEA tools failed to address adequately. It quickly earned acclaim in academic circles for its innovative features and capability to simulate real-world engineering challenges involving non-linear and dynamic factors. In 1980, Dr. ABAQUS established ABAQUS, Inc. to commercialize the software. This transition allowed the software to evolve from a tool for academic research into a marketable product. Over the following twenty years, ABAQUS expanded by incorporating additional functionalities, such as heat transfer analysis, dynamic simulations, and optimization. Throughout this period, ABAQUS became increasingly popular across various industries, including automotive, aerospace, civil engineering, and energy.

In 2005, ABAQUS was purchased by Dassault Systems, a prominent company in 3D design and product lifecycle management (PLM). This acquisition enabled ABAQUS to leverage Dassault's vast resources, resulting in further improvements in simulation capabilities. ABAQUS was incorporated into the SIMULIA software suite, enhancing its performance in multi-physics simulations and high-performance computing (HPC). Today, ABAQUS stands as one of the most advanced and widely utilized FEA tools worldwide. In 2005, ABAQUS was purchased by Dassault Systems, integrating it into the SIMULIA suite of simulation tools. This acquisition enabled ABAQUS to enhance its functionalities, incorporating multi-physics simulations, high-performance computing, and cloud-based options. Currently, ABAQUS is a leading FEA software, extensively utilized for its sophisticated simulation features in structural, thermal, and multi-physics analysis, catering to industries ranging from aerospace to energy.

B. Development of ABAQUS Software

The evolution of ABAQUS has been largely influenced by the growing necessity for advanced simulation tools in engineering, especially to represent intricate physical behaviours that traditional analytical techniques struggle to address. Initial iterations of ABAQUS concentrated mainly on structural analysis, particularly related to issues involving significant deformations and non-linear material behaviours like plasticity and viscoelasticity.

Throughout the years, ABAQUS has significantly broadened its functionalities. During the 1990s, the software included more sophisticated material models, multi-physics features, and capabilities for dynamic simulations. ABAQUS also added functions for managing contact issues, heat transfer, and fluid-structure interactions, thus becoming a flexible tool used by engineers in various sectors.

The acquisition by Dassault Systems in 2005 represented a pivotal moment in ABAQUS's growth, as it was incorporated into the SIMULIA brand, which encompasses a variety of simulation tools. Since becoming part of Dassault, ABAQUS has continued to progress, achieving major advancements in parallel processing, cloud computing, and multi-scale simulations. The software now integrates smoothly with other Dassault offerings, facilitating a comprehensive approach to product design, simulation, and optimization.

C. Operations

ABAQUS utilizes the finite element method (FEM), a computational approach employed to tackle intricate engineering challenges. The software divides a physical structure into a mesh of small, linked elements that embody the physical system. Each element can be characterized by its material properties, boundary conditions, and loading conditions. By implementing the FEM, the governing equations of the physical scenario are solved, yielding a solution that approximates the structural response under different conditions.

ABAQUS functions in two main modes: ABAQUS/Standard and ABAQUS/Explicit:

ABAQUS/Standard is the general-purpose solver suited for both static and dynamic issues that are relatively linear or involve slow, steady processes like quasi-static deformation, heat transfer, and structural analysis. It employs implicit methods to resolve the system of equations.

ABAQUS/Explicit is designed for modelling highly dynamic events, including crash analysis, blast loading, and other transient scenarios. It utilizes explicit time integration, which is more effective for problems characterized by short timeframes and significant non-linear behavior. Additionally, the software features ABAQUS/CAE (Complete Abaqus Environment), which offers a comprehensive graphical interface for pre-processing, simulation, and post-processing tasks. ABAQUS/CAE enables users to define geometry, material characteristics, mesh configurations, boundary conditions, and loads, as well as to visualize results.

D. Uses of ABAQUS Software

ABAQUS is extensively utilized in various industries for numerous applications that demand sophisticated simulation capabilities. Some of its primary functions include:

1. Structural Evaluation: ABAQUS is employed to assess the durability, rigidity, and stability of structures under a variety of loading scenarios. It finds application in fields such as construction design, automotive crash testing, aerospace, and mechanical component engineering.
2. Material Representation: ABAQUS offers support for an extensive array of material models, including metals, polymers, composites, and innovative materials like foams, ceramics, and biological tissues. This enables engineers to mimic real-world materials and forecast their performance under different conditions, such as plastic deformation, fracture, and fatigue.
3. Non-linear Simulation: ABAQUS excels at modelling non-linear issues, including those that entail significant deformations, plastic behavior, or intricate contact interactions. This makes it appropriate for applications like stamping, welding, and forming processes within the manufacturing sector.
4. Multi-physics Simulations: ABAQUS is capable of simulating interconnected multi-physics scenarios, such as fluid-structure interaction (FSI), heat transfer, and electromagnetic effects. This feature is advantageous for industries needing to simulate systems with related physical phenomena, such as aerospace and automotive.
5. Dynamic Evaluation: ABAQUS can model dynamic scenarios like vibrations, shocks, and impacts, making it well-suited for applications involving crash testing, seismic assessments, and modal analysis.
6. Optimization and Design: ABAQUS facilitates optimization methods that assist engineers in creating structures that are both efficient and economical by reducing material consumption while maintaining structural integrity.

E. Advantages

1. Advanced Simulation Features: ABAQUS offers state-of-the-art capabilities for modelling intricate, non-linear behaviours, such as large deformations, material yielding, and contact issues, making it ideal for addressing real-world engineering problems.
2. Multi-physics and Multi-scale Analysis: The software's proficiency in executing multi-physics simulations, including fluid-structure interaction, thermal dynamics, and electro-mechanical challenges, enables engineers to represent complex systems with interrelated physical processes.
3. Extensive Range of Material Models: ABAQUS accommodates a wide array of material models, covering metals, composites, and advanced materials, facilitating the simulation of various engineering scenarios.
4. Exceptional Performance: With capabilities for parallel computing and high-performance computing (HPC), ABAQUS is capable of managing large-scale simulations, making it well-suited for industries that require in-depth analysis of complicated, extensive systems.
5. User-Friendly Design: ABAQUS/CAE features an engaging graphical interface for pre-analysis, solving, and post-analysis tasks, making the software approachable for both beginners and experienced users.
6. Seamless Integration with Other Dassault Systems Tools: As a component of the SIMULIA suite, ABAQUS integrates effortlessly with other Dassault solutions for product design and lifecycle management, creating a thorough platform for simulation-driven product development.

F. Disadvantages

1. High Cost: ABAQUS is a commercial software, and the cost of licensing can be prohibitively expensive for small businesses or academic institutions without sufficient funding.
2. Complexity: While the graphical interface is user-friendly, the software's advanced capabilities can be overwhelming for novice users. Proper training is often required to fully utilize its potential.
3. High Computational Requirements: ABAQUS simulations, especially those involving large-scale models or complex multi-physics problems, can be computationally intensive and require access to powerful hardware or high-performance computing resources.
4. Steep Learning Curve: For users new to FEA or simulation tools, mastering ABAQUS's extensive features and capabilities may take significant time and effort.
5. Limited Post-Processing Capabilities: Although ABAQUS provides powerful post-processing tools, some users may find it lacking compared to other specialized post-processing software that offers more advanced visualization techniques.

G. Applications

ABAQUS is utilized across a range of industries, and its sophisticated simulation features are leveraged to enhance designs, ensure safety, and lower costs. Some key applications include:

1. Automotive Industry: In vehicle design, ABAQUS conducts crash simulations, structural optimization, and fatigue assessments. Its capacity to replicate intricate material behaviours and dynamic events is vital for maintaining safety and performance in automotive engineering.
2. Aerospace: The aerospace sector applies ABAQUS for evaluating lightweight structures, thermal protection systems, and aeroelasticity. Its ability to model high-stress conditions, typical in aircraft and spacecraft operations, is essential for aerospace engineers.
3. Civil Engineering: In civil engineering, ABAQUS is used for the design of buildings, bridges, and various other infrastructures. It plays a role in seismic analysis, monitoring structural health, and assessing materials under severe loading situations.
4. Manufacturing: ABAQUS finds extensive use in manufacturing for processes such as sheet metal forming, plastic moulding, and welding simulations. It aids in refining manufacturing techniques, enhancing product quality, and minimizing material wastage.
5. Energy: Within the energy industry, ABAQUS is employed to analyse nuclear reactors, wind turbines, and additional energy infrastructure. It evaluates the structural integrity and performance of components subjected to extreme conditions like high temperatures or fluid dynamics.
6. Biomedical Engineering: In biomedical engineering, ABAQUS simulates the behavior of biological tissues, implants, and medical devices. It supports the development of safer and more effective prosthetics, orthopaedic devices, and surgical instruments.

IV. LITERATURE REVIEW

Experiments on castellated beams provide important new information on their structural behavior, especially with reference to design optimization, buckling resistance, and load capacity [16]. The performance of castellated beams under diverse situations is assessed in these works using a variety of approaches, such as numerical analysis and experimental testing. Research indicates that castellated beams with smaller hexagonal openings (140mm) exhibit an increase in load capacity by approximately 11.11% compared to larger openings (280mm). The use of full interaction shear connectors enhances the ultimate load capacity, with increases of about 6% noted for beams with smaller openings [17]. The local buckling of webs significantly influences the bearing capacity of castellated beams. Studies show that local web buckling can increase the bearing capacity by 27.3% [18]. The geometry of the web openings, including their shape and angle, affects the buckling resistance and overall performance of the beams [19]. Optimization studies demonstrate that castellated beams can achieve a reduction in material usage (up to 23.19%) while maintaining load-carrying capacity, particularly when using hexagonal openings [20]. The integration of trapezoidal corrugated webs further enhances resistance to buckling, making these beams a viable option for modern construction [21].

Significant improvements in structural performance, especially in load-carrying capacity and deflection characteristics, are revealed by ABAQUS software analysis of castellated beams. Numerous researches have used ABAQUS to investigate various castellated beam geometries and combinations, emphasizing the benefits of these beam designs over more conventional ones. Studies show that castellated beams can support heavier loads [22]. Hexagonal-opening beams, for example, demonstrated a 13% material savings over conventional I beams [23]. The results detail that the corrugated web rectangular castellated beams have less weight and more strength than the corrugated web hexagon castellated beam. Buckling resistance is greatly increased by including trapezoidal corrugated webs. Reactive powder concrete encasement and other strengthening methods reduced deflection by as much as 60.55% [24]. Research has examined a range of web opening designs, such as circular, arch, and hexagonal openings, and the results indicate that distinct geometries may improve performance. Arch-shaped apertures, for instance, increased load capacity by 27% [25]. For thorough modelling, ABAQUS has been used in conjunction with other programs like as ANSYS. This has enabled a thorough examination of failure patterns and deflection under load [26][18]. FEM analysis has been utilized to assess lateral-torsional buckling in castellated beams. The results confirmed that the presence of openings affects critical buckling loads, necessitating careful design considerations [27]. Incorporating stiffeners within the web openings has been shown to enhance load capacity and reduce failure risks, highlighting the importance of design modifications in improving structural integrity [28].

V. MODELLING OF CASTELLATED BEAMS

To model and analyze a castellated beam in Abaqus, several essential steps are required:

1. Geometry Creation: Start by designing a 3D deformable component that represents the beam. Typically, an I-beam cross-section is utilized. Employ the “Sketch Tool” to outline the holes in the web (commonly hexagonal or circular), and apply an Extrude Cut to eliminate material, creating the castellated design.
2. Material Definition: Specify the material properties, including Young’s Modulus, Poisson’s Ratio, and Yield Strength in the “Material” section. Assign this material to the beam component by forming a solid section.
3. Assembly: In the “Assembly” section, position the component within the model space. If multiple components are involved, ensure they are placed correctly.
4. Meshing: Generate a mesh for the component utilizing Hexahedral or Quadrilateral elements. Make sure to use a finer mesh around the castellated holes to accurately capture stress concentrations.
5. Boundary Conditions and Loads: In the “Load” section, impose boundary conditions (such as fixed or simply supported) and apply loads (like point loads or uniformly distributed loads).
6. Analysis: Set up a job for a Static General analysis in the “Job” section and submit it for simulation.
7. Post-Processing: Examine the results in the “Visualization” section, focusing on displacement, stress, and strain, particularly around the castellated holes to evaluate performance and identify potential failure areas.

VI. MATERIALS AND METHODOLOGY

The static behavior of castellated web beams with different shaped web apertures is examined in this study using the finite element method (FEM). The reactions of these beams under various situations are thoroughly simulated using the sophisticated program ABAQUS. The primary objective is to evaluate the static performance of castellated web beams, whose structural characteristics are greatly influenced by the distinctive apertures in their web sections. Investigating the complex relationships between the beam shape, material properties, and the impact of the web apertures is the aim of this work. The FEM is essential to the analysis in order to do this since it simplifies complicated beam constructions into smaller, easier-to-manage components, enabling the modelling of their behavior in a variety of conditions.

To do these simulations with a high level of precision, ABAQUS is used. Following a detailed discussion of the various element types used in the study, with an emphasis on the particular structural components involved, the research provides a comprehensive review of the material qualities and their characteristics. Furthermore, the study comprises a careful analysis of the geometric configurations and beam diameters. An I section beam of span 3m, width 200mm and depth 300mm is considered along with web and flange thickness of 10 mm. Six sorts of web openings are examined; Figure 1 to 6 provides a representation of castellated beams with various type of opening. Six beams are produced as a consequence of the design process with 5 different shapes namely, circle, triangle, square, pentagon, hexagon, and without opening. The apertures are made so that the area of the openings in the castellated beams varies, but their circumcircle remains same. The material characteristics used in the analysis are 2×10? MPa for Young's modulus (E) and 0.29 for Poisson's ratio (υ). The beam structure is constrained by fixed-fixed boundary conditions, which limit both rotation and translation at its endpoints. A uniform distributed load of 20 N/mm² is applied across the entire length of the beam. To enhance the precision of the analysis, the beam is divided into smaller elements using a meshing technique. This meshing approach effectively segments the beam into smaller sections, allowing for a comprehensive simulation of its response under the specified loading conditions and boundary restrictions. The meshing procedure is crucial for obtaining dependable outcomes in finite element analyses, such as the one performed in this study. Figure 6 represents an typical model of castellated beam with supports and loading frame where as figure 7 shows the assignment of loading and boundary conditions. Figure 8 represents the messed castellated beam.

Fig. 1  Castellated beam with Circular opening

Fig. 2 Castellated beam with Triangular opening

Fig. 3 Castellated beam with Square opening

Fig. 4 Castellated beam with Pentagonal opening

Fig. 5 Castellated beam with Hexagonal opening

Fig. 6 Castellated beam without opening

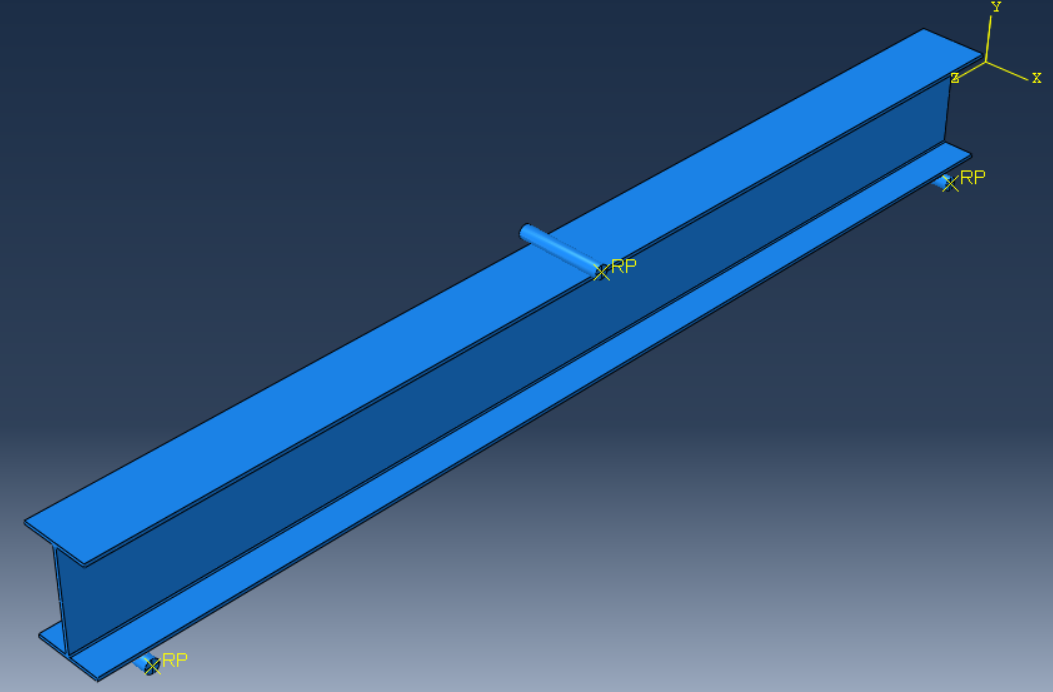Fig. 7 Modelling of castellated beam without web openings and supports provided.

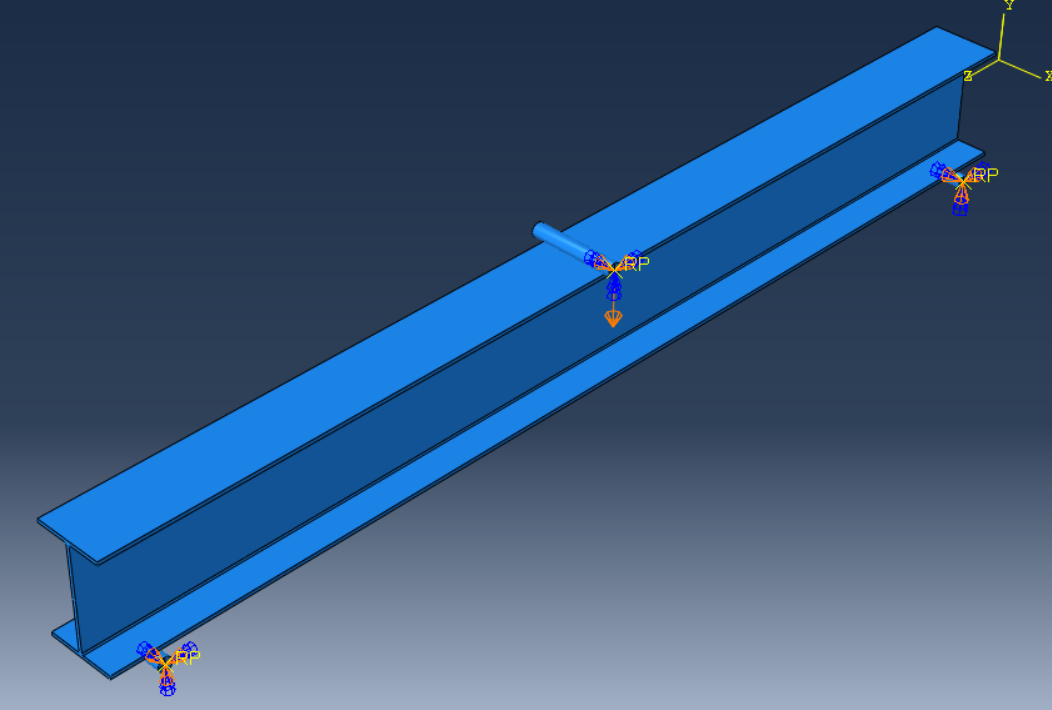Fig. 8 Assigning loading and boundary conditions to castellated beam.

Fig. 9 Messing of castellated beam.

VII. RESULTS AND DISCUSSION

The flexural response of all castellated beams with varying web apertures under external loads is clearly depicted in Figure 10, which also successfully illustrates the deflection behavior of these beams. It can be observed that the deflection of the beams follows same pattern as load applied is varied, irrespective of the type of web opening is provided in beams. It is clear that the castellated beams, irrespective of the kind of opening, have a load-carrying capacity between 61.99 and 73.94 kN, whereas the unaltered beam with no web apertures has a slightly greater load capacity of 81.40 kN.  This demonstrates unequivocally that whereas smaller area apertures often exhibit a greater capacity, bigger web openings result in a comparatively reduced load-carrying ability. Furthermore, it is observed that the displacement variation pattern in proportion to applied force is comparable for all castellated beams with different aperture types. Figure 11 & 12 shows maximum and minimum stresses observed in the castellated beam. Maximum stresses are found at the point of application of load applied at the mid span of the beam. And minimum stresses are observed around the supports provided to the beam section, in all the castellated beams irrespective of the web openings provided. Similar pattern of maximum and minimum stresses are observed even for the beam without any web openings.

Conclusion

The configuration of openings in a castellated beam significantly influences its ability to carry loads. Pentagonal openings allow for efficient material distribution, whereas square ones create stress concentrations at their corners. Castellated beams with pentagonal openings feature optimum reduction in cross-sectional areas compared to other beams with various shapes of opening, without compromising in the load carrying capacity. While circular beams provide uniform load distribution, they may not utilize material as effectively. Circular shapes are effective in evenly distributing stress, but squares can lead to stress concentration at their corners, which could result in failure. Castellated beams with pentagonal openings facilitate improved load distribution, thereby enhancing structural integrity. These shapes consistently exhibit a highly beneficial and even load distribution. The foundation for this behavior can be traced to the unique geometric properties of polygon openings and reduced web area. These features allow for the effective transfer of loads through well-defined pathways that extend along the beam\'s length. Ultimately, the analysis has highlighted the crucial significance of geometric properties and web area in influencing load distribution and overall load-bearing performance.

References

S. Elaiwi, B. Kim, and L.-Y. Li, “Bending Analysis of Castellated Beams,” Athens J. ?echnology Eng., vol. 6, no. 1, pp. 1–16, Feb. 2019, doi: 10.30958/ajte.6-1-1. [2] R. Frans, H. Parung, D. Sandy, and S. Tonapa, “Numerical Modelling of Hexagonal Castellated Beam under Monotonic Loading,” in Procedia Engineering, Elsevier Ltd, 2017, pp. 781–788. doi: 10.1016/j.proeng.2017.01.449. [3] K. D. Tsavdaridis and C. D’Mello, “Web buckling study of the behaviour and strength of perforated steel beams with different novel web opening shapes,” J. Constr. Steel Res., vol. 67, no. 10, pp. 1605–1620, Oct. 2011, doi: 10.1016/j.jcsr.2011.04.004. [4] S. DOORI and A. R. NOORI, “Finite Element Approach for the Bending analysis of Castellated Steel Beams with Various Web openings,” ALKÜ Fen Bilim. Derg., vol. 3, no. 2, pp. 38–49, Aug. 2021, doi: 10.46740/alku.883187. [5] V. Agrawal and D. Bhatt, “A Design Comparison of Castellated Beam for Different Parameters,” EasyChair, Jan. 2018, pp. 403–395. doi: 10.29007/cz65. [6] R. R. Kurlapkar, A. P. Patil, and P. D. Kumbhar, “Analyzing the influence of perforations on the structural behavior of mild steel cellular beams,” Asian J. Civ. Eng., vol. 25, no. 2, pp. 1385–1394, Feb. 2024, doi: 10.1007/s42107-023-00849-1. [7] A. Kadam and S. B. Shinde, “Review on comparative study of castellated beam with different web openings,” 2020. [8] S. Kale, V. Kadlag, and S. Kulkarni, “Study Behaviour of Castellated Beam with Diagonal Stiffeners within and Outside the Opening by Using ABAQUS Software,” Int. Res. J. Eng. Technol., 2018, [Online]. Available: www.irjet.net [9] P. Ravi, “Performance Analysis of Castellated Beams with Different Web Openings.” [Online]. Available: www.ijert.org [10] S. G. Morkhade, T. Shirke, A. Mansuke, M. U. Chavan, and L. M. Gupta, “Experimental and Analytical Investigation of Castellated Steel Beams with Varying Openings Eccentricity,” J. Inst. Eng. Ser. A, vol. 102, no. 2, pp. 479–488, Jun. 2021, doi: 10.1007/s40030-021-00516-1. [11] A. S. Shaikh and H. R. Aher, “International Journal on Recent Technologies in Mechanical and Electrical Engineering (IJRMEE) Structural Analysis of Castellated Beam,” 2015, [Online]. Available: http://www.ijrmee.org [12] F. Menkulasi, C. D. Moen, M. R. Eatherton, and D. Kuruppuarachchi, “Investigation of Stiffener Requirements in Castellated Beams.” [13] M. R. Soltani, A. Bouchaïr, and M. Mimoune, “Nonlinear FE analysis of the ultimate behavior of steel castellated beams,” J. Constr. Steel Res., vol. 70, pp. 101–114, Mar. 2012, doi: 10.1016/j.jcsr.2011.10.016. [14] Samadhan G. Morkhade and Laxmikant M. Gupta, “Behavior of Castellated Steel Beams: State of the Art Review,” Electron. J. Struct. Eng., vol. 19, pp. 39–48, Dec. 2019, doi: 10.56748/ejse.19234. [15] M. E. A. Ben Seghier, H. Carvalho, C. C. de Faria, J. A. F. O. Correia, and R. H. Fakury, “Numerical analysis and prediction of lateral-torsional buckling resistance of cellular steel beams using FEM and least square support vector machine optimized by metaheuristic algorithms,” Alexandria Eng. J., vol. 67, pp. 489–502, Mar. 2023, doi: 10.1016/j.aej.2022.12.062. [16] S. J. S and S. K. N, “ANALYSIS AND OPTIMIZATION OF CASTELLATED WEB BEAMS WITH VARIED WEB OPENING SHAPES USING ABAQUS SOFTWARE.” [17] M. A. Qasim and W. A. Waryosh, “Behavior of Concrete Beam Encasing Castellated Steel Section with Different Opening Size,” vol. 2, no. 2, pp. 302–310, 2024. [18] Muthukkumaran C, Karthikeyan S, and Satheesh Kumar K R P, “Structural Behaviour of Castellated Beam: A Review,” Int. J. Adv. Res. Sci. Commun. Technol., vol. 3, no. 1, pp. 83–87, 2023, doi: 10.48175/ijarsct-9011. [19] I. Barkiah, A. R. Darmawan, and N. Agusniansyah, “The Latest Innovations in the Flexural Capacity of Castellated Beams with Hexagonal Stiffener Variations,” Preprints, Aug. 2024, doi: 10.20944/preprints202408.0201.v1. [20] V. Yurchenko, I. Peleshko, and P. Rusyn, “Optimization of Cross-Sectional Dimensions of Castellated Beams With Hexagonal Openings,” Eastern-European J. Enterp. Technol., vol. 3, no. 7(129), pp. 6–16, 2024, doi: 10.15587/1729-4061.2024.304803. [21] A. V and P. Dilip P, “Numerical Analysis of Corrugated Castellated Beam with and Without Openings,” J. Civ. Constr. Eng., vol. 10, no. 2, pp. 15–24, 2024, doi: 10.46610/jocce.2024.v010i02.003. [22] M. P. Pooja Rugge Pallavi K Pasnur ME Student Assistant Professor, “Review on Study of Castellated Beam with &without Stiffeners,” 2017. [Online]. Available: www.ijste.org [23] Arifa V, Priyanka, and Dilip P, “Numerical Analysis of Corrugated Castellated Beam with and Without Openings,” J. Civ. Constr. Eng., vol. 10, no. 2, pp. 15–24, 2024, Accessed: Dec. 25, 2024. [Online]. Available: doi: 10.46610/jocce.2024.v010i02.003 [24] N. Y. Abbas, A. Jabbar, and H. Alshimmeri, “Journal of engineering physics,” Int. J. Heat Mass Transf., vol. 8, no. 7, p. 1052, 1965, doi: 10.1016/0017-9310(65)90089-x. [25] Upadhyay M H, Vishal B P, and Vishal A A, “Parametric Study On Castellated Beam With Arch-Shape Openings,” SSRG Int. J. Civ. Eng., vol. 8, no. 5, pp. 52–57, 2021. [26] V. Keerthika and D. Daniel Thangaraj, “Numerical Analysis on Load Carrying Capacity of Castellated Beam by Varying Web Opening,” in Proceedings of the Indian Structural Steel Conference 2020 (Vol. 1), M. Madhavan, J. S. Davidson, and N. E. Shanmugam, Eds., Singapore: Springer Nature Singapore, 2024, pp. 527–540. [27] S. A. Patil and P. D. Kumbhar, “STUDY OF CASTELLATED BEAM USING STIFFENERS: A REVIEW.” [Online]. Available: http://www.ijret.org [28] D. Nikhil and K. Ashok, “Parametric study of castellated beam with coupled stiffener,” Int. J. Adv. Res., vol. 7, no. 09, pp. 246–252, 2019, [Online]. Available: www.IJARIIT.com

Copyright

Copyright © 2024 Bharat Singh Uikey, Dr. Umesh Pendharkar, Chaitra A. R.. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.