Combined Loading Effects on the Buckling Strength of Q690 Steel Tubes: An Experimental and Numerical Study

Abstract

This study investigates the stability and buckling behavior of Q690 high-strength steel cylindrical tubes subjected to combined axial compression and bending loads. Experimental testing on 27 specimens, combined with finite element analysis using ABAQUS, revealed critical insights into load-bearing capacity, deformation patterns, and failure modes. The study found that geometric imperfections, such as initial out-of-roundness and local dents, and residual stresses significantly influenced the buckling strength of the tubes, particularly those with high diameter-to-thickness ratios. Finite Element Analysis (FEA) effectively modeled the complex behavior, with deviations from experimental results ranging from 5.6% to 7.9%. Based on these findings, design recommendations, including optimized D/t and slenderness ratios, are proposed to enhance structural safety and efficiency. These results contribute to a better understanding of Q690 steel behavior and can inform the development of improved design codes for critical infrastructure applications.

Introduction

I. INTRODUCTION

Cylindrical steel tubes are widely employed in critical infrastructure, serving as essential components in structures such as bridges, wind turbines, offshore platforms, and transmission towers. Their inherent strength and durability make them ideal for supporting significant loads and resisting various environmental forces. However, ensuring the stability and load-carrying capacity of these tubes under complex loading scenarios remains a crucial challenge for engineers.

One of the primary concerns is the potential for buckling, a phenomenon where a structural member suddenly experiences a significant and often irreversible deformation under compressive loads. This instability can lead to catastrophic failures, jeopardizing the safety and functionality of the entire structure.

In recent years, high-strength steels like Q690 have gained significant traction in structural engineering. These advanced materials offer a compelling combination of high yield strength and excellent ductility, enabling the design of lighter and more efficient structures. However, the use of high-strength steels introduces new complexities. Factors such as geometric imperfections (e.g., initial out-of-roundness, local dents) and residual stresses (induced during manufacturing processes like welding and cold forming) can significantly influence the buckling behavior of these materials.

Fig. 1 Stages of Cement Silo Failure on Steel Structure

Fig. 1 illustrates a potential failure scenario in a steel structure, highlighting the importance of understanding buckling behavior. The figure depicts the stages of a cement silo failure, likely triggered by a combination of factors, including buckling instability. This visual representation emphasizes the potential consequences of inadequate structural design and the critical need for thorough research in this area.

A. Background

The rapid growth of ultra-high-voltage (UHV) substations in China has increased the need for efficient, cost-effective structures. High-strength steel (HSS), particularly Q690, offers advantages such as reduced material use, lower costs, and improved performance. Despite advancements in steel production, current design standards often rely on lower-strength steels like Q420, limiting the benefits of HSS.

Q690’s mechanical properties significantly affect structural stability under complex loads, but issues like buckling behavior and residual stresses remain underexplored. This study investigates Q690 steel tubes under combined axial compression and bending to address these gaps, enhance design codes, and promote its use in critical infrastructure.

B.  Problem Statement

Cylindrical steel tubes are commonly used in critical infrastructure under combined axial compression and bending. These loading conditions lead to complex interactions that impact tube stability, resulting in buckling modes such as global, local, and distortional buckling. High-strength steels like Q690, while offering superior strength, are more susceptible to buckling due to imperfections and residual stresses from manufacturing.

Current design codes do not adequately account for these complexities, leading to inaccurate predictions and overly conservative designs. Research on combined axial and bending loads in high-strength steels is limited, and experimental data is scarce due to cost and time constraints. Finite Element Analysis (FEA) provides a promising solution but requires balancing accuracy with computational efficiency.

This study aims to:

1. Investigate the buckling behavior of Q690 steel tubes under combined loading.
2. Analyze the effects of imperfections, residual stresses, and material properties.
3. Develop predictive models for better design guidelines in critical infrastructure.

C. Research Objectives

The primary aim of this research is to explore the stability and buckling behavior of Q690 high-strength steel cylindrical tubes under combined axial compression and bending. The study combines experimental testing with numerical simulations to understand the interaction between these loading conditions. Specific objectives include:

1. Investigating the buckling behavior of Q690 steel tubes under combined loading, focusing on failure modes and mechanisms.
2. Analyzing the impact of geometric imperfections and residual stresses on stability and failure, considering manufacturing defects.
3. Validating numerical models with experimental results to ensure accuracy in predicting structural behavior.
4. Developing practical design guidelines to improve the safety, efficiency, and economic performance of structures using Q690 steel tubes, with recommendations for integrating them into existing design codes.

II. LITERATURE REVIEW

The stability and behavior of cylindrical tubes fabricated from high-strength steel Q690 under combined axial compression and bending loads have been investigated extensively. This section reviews existing research relevant to this topic, focusing on the mechanical properties of Q690, buckling theories, the influence of combined loading, and the effects of geometric imperfections and residual stresses. Additionally, the importance of finite element analysis (FEA) in structural engineering is highlighted, and the gaps in current research are identified.

A. Mechanical Properties of High-Strength Steel (HSS)

High-strength steel (HSS) generally refers to steel with a nominal yield strength exceeding 460 N/mm² [1]. However, the specific definition varies across sectors [1]. Q690 steel, with a nominal yield strength of 690 MPa, offers superior mechanical properties, including high yield strength, improved ductility, enhanced fatigue resistance, and reduced material usage [1, 2, 3].

These characteristics make it suitable for demanding applications such as transmission towers, offshore platforms, and bridges. Studies have shown that Q690 exhibits high yield strength (690 MPa), allowing for lighter structural designs [1, 4]. Improved ductility and strain-hardening characteristics enhance its toughness and energy absorption capacity [5, 6]. Q690 demonstrates high resistance to deformation and cracking, making it suitable for harsh environments [7, 8]. High ultimate tensile strength (typically 800-900 MPa) is beneficial in high-stress applications [9, 10]. HSS offers cost-effectiveness, particularly in long-span structures where dead weight is significant. However, limited expertise, design limitations, and market barriers have hindered its widespread adoption. The COVID-19 pandemic impacted the HSS market due to supply chain disruptions and reduced demand [11].

B. Buckling Theories

Buckling is a structural instability phenomenon where a structure experiences a sudden change in shape due to compressive forces [12]. Euler's work on column buckling laid the foundation for modern buckling analysis [13]. Different buckling modes include bifurcation buckling (e.g., cylindrical shells under axial compression) and snap-through buckling (e.g., spherical domes) [12]. Imperfections can significantly affect the buckling behavior of structures, especially those with unstable post-buckling paths [12]. Classical elastic buckling theory for shells, initially developed for long cylindrical shells under axial compression [14, 15, 16], has limitations when applied to real-world scenarios. Shell buckling can occur through nonlinear collapse or bifurcation buckling [12]. Various theories have been developed to describe the behavior of cylindrical shells under buckling, including Donnell's Theory [17], Timoshenko's Shell Theory [18], Flügge's Theory [19], Sanders' Theory [20], and more advanced nonlinear elastic theories [21, 22, 23].

C. Influence of Combined Loading Conditions

Cylindrical tubes in engineering applications are rarely subjected to pure axial compression or bending. They are more likely to experience a combination of these loads, which can significantly impact their stability and buckling behavior. Research on the buckling of cylindrical shells under combined axial compression and bending is ongoing [46]. Guggenberger et al. [46] investigated the shell buckling behavior under combined axial and bending loads. They found that the critical buckling load is significantly reduced compared to pure axial compression or bending alone [46]. The interaction between the two loading conditions can lead to complex failure modes, making it challenging to predict buckling behavior using traditional design methods

D. Geometric Imperfections and Residual Stresses

Real-world cylindrical tubes are not perfectly geometric, and residual stresses are introduced during the manufacturing process, both of which can significantly affect their buckling behavior.

1. Geometric Imperfections: Even minor deviations from a perfect cylindrical shape can act as initiation points for buckling under load. Weld depressions caused by the welding process are common geometric imperfections in cylindrical tubes and storage silos [26, 27]. These imperfections can significantly reduce the buckling strength of the shell [26, 27].
2. Residual Stresses: Residual stresses arise from the localized heating and cooling associated with welding [29]. In HSS structures, these stresses can affect pressurized stability, fatigue fracture, brittle fracture, and stress corrosion cracking [30, 31, 32].

III. MATERIALS AND METHODOLOGY

A. Workflow for the Analysis of Q690 Steel Tubes Stability

This study employed a comprehensive workflow integrating experimental and numerical methods to investigate the stability and buckling behavior of Q690 steel tubes under combined axial compression and bending. The workflow involved the following key steps:

1. Material Preparation: Q690 high-strength steel was procured, and its material properties, including yield strength, modulus of elasticity, and Poisson's ratio, were experimentally determined.
2. Specimen Fabrication:  Cylindrical specimens with varying slenderness and diameter-to-thickness ratios were fabricated to cover a range of structural behaviors.
3. Experimental Testing: 

• Specimens were subjected to controlled axial compression and incremental bending loads.
• Strain gauges and displacement sensors were used to monitor deformation and internal forces during the tests.
• Data on load, displacement, and failure modes were recorded for subsequent analysis.

1. Finite Element Modeling: 

• Detailed finite element models of the specimens were created using ABAQUS software, incorporating S4R shell elements for the tube and solid elements for the end plates.
• Realistic boundary conditions and material properties were applied to the models.
• Initial geometric imperfections, such as out-of-roundness and local dents, were introduced to simulate real-world conditions.

1. Numerical Analysis:  Linear Buckling Analysis (LBA), Geometrically Nonlinear Analysis (GNA), and Geometrically and Materially Nonlinear Analysis with Imperfections (GMNIA) were conducted to predict buckling loads and analyze the structural response under combined loading.
2. Data Analysis and Interpretation:  Numerical results, including critical loads, failure modes, and deformation patterns, were compared with experimental data to validate the accuracy of the finite element models.
3. Model Validation: 

• The influence of initial imperfections, material properties, and loading conditions on the stability of the steel tubes was analyzed.
• The results were compared with relevant design standards, such as EN 1993-1-6, to evaluate code compliance and identify potential areas for improvement.

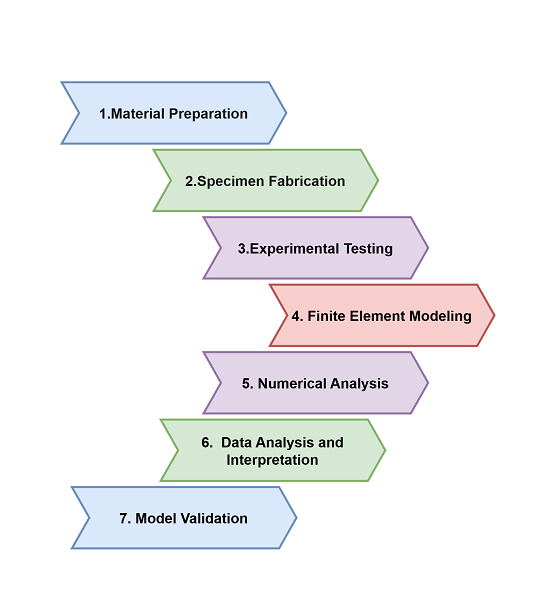
Fig. 2 Workflow for the Analysis of Q690 Steel Tubes Stability

This integrated approach, combining experimental testing with advanced finite element analysis, provided a robust and comprehensive understanding of the stability and buckling behavior of Q690 steel tubes under complex loading conditions.

B. Experimental Study

A total of 27 full-scale specimens with varying slenderness ratios (λ) and diameter-to-thickness (D/t) ratios were tested. Specimens were fabricated from Q690 steel and subjected to controlled axial compression and bending loads. Measurements included strain distribution, axial displacement, and critical buckling moments.

An experimental program was conducted to investigate the compression-bending behavior of Q690 steel tubes. The primary objectives of this experimental study were:

1. Generate reliable empirical data to support the design and application of Q690 steel tubes in engineering structures.
2. Validate the accuracy of existing Chinese design codes for compression-bending strength and stability, including the Steel Code (????) and the Tower Code (????).
3. Provide practical guidance for the design of Q690 steel tube components subjected to combined axial compression and bending loads.

To achieve these objectives, a series of specimens with varying geometric parameters, including slenderness ratio (λ) and diameter-to-thickness ratio (D/t), were fabricated. Each specimen group consisted of three identical tubes, manufactured by Henan Dingli Pole and Tower Co., Ltd., adhering to stringent quality control standards.

A comprehensive experimental setup was employed, utilizing a self-balancing loading frame to ensure accurate and controlled application of axial compression and bending loads. Planar hinged supports were implemented to replicate realistic boundary conditions and minimize unintended constraints. Strain gauges and displacement sensors were strategically placed to monitor deformations and internal forces during the testing process.

The experimental results demonstrated a complex interaction between axial compression and bending loads, leading to nonlinear load-deformation behavior. Two distinct failure modes were observed:

1. Global Instability: characterized by sudden collapse and a sharp drop in load-carrying capacity.
2. Local Instability: characterized by progressive localized buckling and deformation.

The observed failure modes were significantly influenced by the slenderness ratio and diameter-to-thickness ratio of the specimens. Specimens with higher slenderness ratios exhibited a greater propensity towards global instability, while those with lower slenderness ratios were more susceptible to local buckling.

These experimental findings provide a valuable dataset for understanding the structural behavior of Q690 steel tubes under combined loading conditions. This data will be further analyzed and compared with numerical simulations to validate design codes and provide insights for improving the design and application of Q690 steel tubes in engineering structures.

C. Numerical Modeling

Numerical modeling was employed to investigate the buckling behavior of Q690 steel tubes under combined axial compression and bending loads. Finite Element Analysis (FEA) was performed using ABAQUS to simulate the structural response. Three-dimensional models of the tubes were created, incorporating accurate geometric dimensions and material properties obtained from experimental data. The models were discretized using 4-node shell elements, ensuring adequate mesh refinement, particularly in regions prone to high stress concentrations. Boundary conditions were applied to replicate the experimental setup, including fixed and free ends with appropriate constraints. Axial compression and bending loads were applied sequentially to simulate the combined loading scenario. To account for real-world conditions, initial geometric imperfections (out-of-roundness, local dents) and residual stresses were introduced into the models.

Various analysis techniques were employed, including linear buckling analysis (LBA), geometrically nonlinear analysis (GNA), and geometrically and materially nonlinear analysis with imperfections (GMNIA). The GMNIA provided the most comprehensive simulation of the structural response, considering geometric and material nonlinearities, as well as initial imperfections and residual stresses. The numerical results, including buckling loads and deformation patterns, were compared with experimental data to validate the accuracy of the models. Parametric studies were conducted to investigate the influence of various parameters, such as slenderness ratio and diameter-to-thickness ratio, on the buckling behavior of the tubes.

The numerical modeling approach provided valuable insights into the buckling behavior of Q690 steel tubes under combined loading conditions, aiding in the development of improved design guidelines

IV. RESULTS AND DISCUSSION

A. Experimental Observations

The experimental program revealed distinct failure modes in Q690 steel tubes under combined axial compression and bending.

1. Overall Instability: Six specimen groups (DPY9, DPY8, DPY7, DPY7A, DPY5, and DPY4) exhibited overall instability. This failure mode was characterized by a sudden and catastrophic loss of load-carrying capacity, typically observed in specimens with higher slenderness ratios. The bending moment-axial displacement relationship for these specimens demonstrated a nonlinear trend, culminating in a sharp drop in load-bearing capacity.
2. Local Instability: Three specimen groups (DPY6, DPY2, and DPY1) experienced local instability. This failure mode was characterized by a more gradual deformation process, with localized buckling occurring near the bending moment application point. The load-carrying capacity declined more gradually compared to overall instability.
3. Premature Failures: Three specimens (DPY1-1, DPY1-2, and DPY4-2) experienced premature failure during the axial loading phase, likely due to manufacturing defects or unforeseen anomalies. These specimens were excluded from the primary analysis.
4. Measurement Limitations: Accurate measurement of certain deformations, such as angular displacement, proved challenging due to the scale and complexity of the test setup.

These observations provide a foundation for understanding the complex failure mechanisms of Q690 steel tubes under combined loading conditions. Further analysis will delve deeper into the factors influencing these failure modes, including slenderness ratio, diameter-to-thickness ratio, and the magnitude of applied loads.

B. Critical Load Capacity Analysis and Comparison with Design Codes

This section evaluates the critical load capacities of the tested specimens by comparing experimental results with predictions from existing design codes. The Steel Construction Code (????) provides formulas for bending component strength and overall stability, while the Tower Regulations (????) and American Rod Regulations (????) offer guidance on local buckling stability.

TABLE I
Comparison of Measured and Calculated Critical Load Capacities

Fig 3 presents a graphical comparison of the measured bending moments with the values calculated using various design codes.

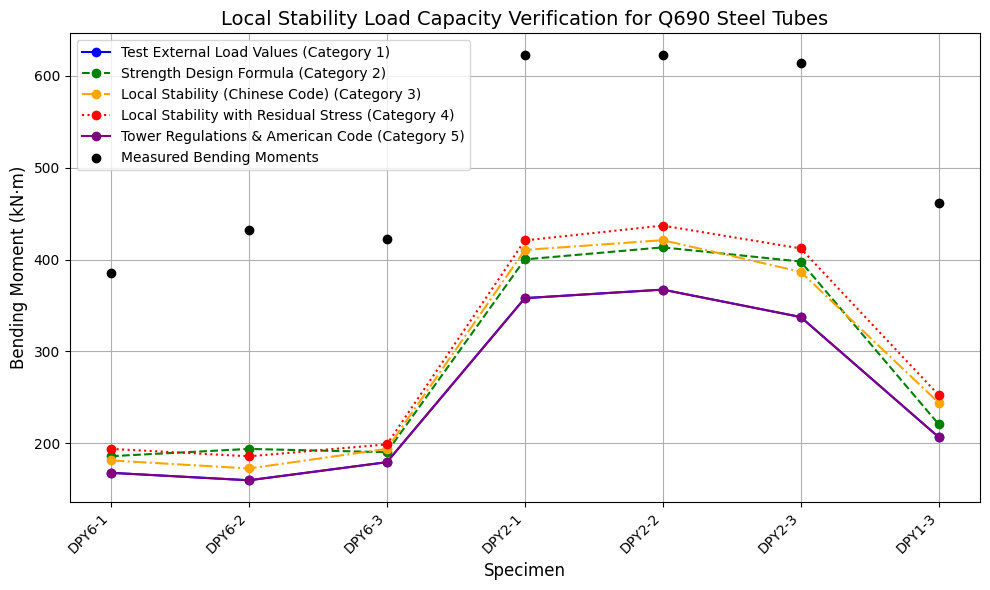
Fig. 3 Comparison of Measured and Calculated Critical Load Capacities for Q690 Steel Tubes

This comparison allows for a critical evaluation of the accuracy and applicability of existing design codes in predicting the critical load capacities of Q690 steel tubes under combined loading conditions.

C. Failure Modes

The experimental investigation revealed two primary failure modes for Q690 steel tubes under combined bending and axial compression:

1. Overall Buckling: Specimens with higher slenderness ratios exhibited overall buckling, characterized by sudden and catastrophic failure. This mode involved a rapid loss of load-carrying capacity and significant bending deformation across the entire tube length.
2. Local Buckling: Observed in specimens with lower slenderness ratios, local buckling manifested as localized deformation, often near the bending moment application point. This failure mode was characterized by a more gradual decline in load-carrying capacity compared to overall buckling.

These distinct failure modes were observed across all specimen groups, highlighting the influence of geometric parameters and loading conditions on the structural behavior of Q690 steel tubes.

D. Moment and Axial Displacement Relationship

This section presents a detailed analysis of the relationship between bending moment and axial displacement for each specimen group, comparing experimental results with finite element simulations under various initial imperfection conditions.

1. Nonlinear Pre-failure Behavior: A nonlinear relationship between bending moment and axial displacement was observed in all specimens, particularly influenced by the initial axial load. The nonlinearity was more pronounced in specimens with higher slenderness ratios, indicating a more significant influence of geometric imperfections on the structural response.
2. Overall Instability Failure: All specimens exhibited overall instability, characterized by a sudden and catastrophic loss of load-carrying capacity. This failure mode was triggered by the combined effects of axial compression and bending moment, leading to global buckling of the entire tube section.
3. Influence of Initial Imperfections: Residual stresses were found to have a more significant impact on the simulated bending moments compared to local geometrical imperfections. This suggests that the presence of residual stresses, often induced during manufacturing processes, can significantly reduce the load-carrying capacity of Q690 steel tubes.
4. Model Accuracy: The finite element model accurately predicted bending stiffness, demonstrating its ability to capture the elastic and inelastic deformation behavior of the tubes. However, the model consistently overestimated axial stiffness, indicating a need for further refinement of the constitutive models and numerical techniques to accurately represent the axial deformation behaviour.

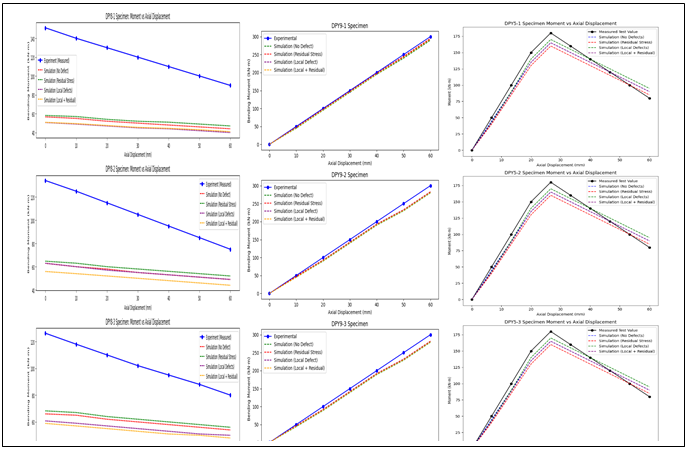
.Fig. 4 Comparison of Experimental and Simulated Moment-Axial Displacement Curves (DPY5,8,9)

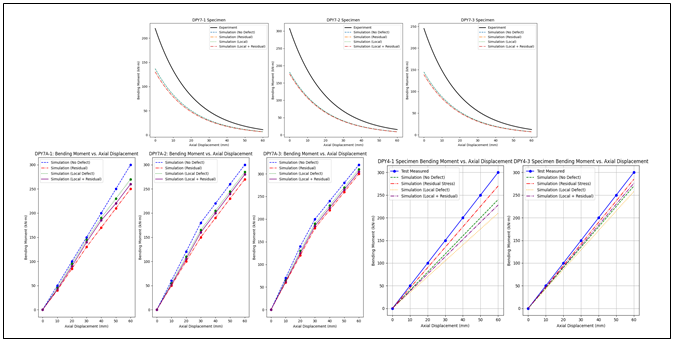
Fig. 5 Comparison of Experimental and Simulated Moment-Axial Displacement Curves (DPY4,7,7A)

Fig. 4 and Fig. 5 presents a comprehensive comparison of the experimental and simulated moment-axial displacement curves for all specimen groups. This figure visually illustrates the key findings, including the nonlinear pre-failure behavior, the sharp drop in load-carrying capacity at failure, and the influence of initial imperfections on the structural response.

E. Critical Bending Strength and Influence of Imperfections

Fig. 6 shows the comparison of the critical bending strength (simulated bending moment) of the specimens that experienced global instability under different defect conditions. The critical bending strength is significantly influenced by the presence of initial imperfections, particularly residual stresses.

Fig. 6 Comparison of Critical Bending Strength for Specimens Experiencing Global Instability

1. Effect of Residual Stresses: The introduction of residual stresses consistently resulted in a significant reduction in the predicted critical bending strength. This highlights the crucial role of residual stresses in the overall stability and load-carrying capacity of Q690 steel tubes.
2. Influence of Local Geometric Imperfections: The effect of local geometric imperfections on the critical bending strength was generally less pronounced compared to residual stresses. However, in some cases, local imperfections were observed to have a noticeable impact, further emphasizing the importance of considering both types of imperfections in the design and analysis process.

These findings underscore the need to incorporate the effects of initial imperfections, particularly residual stresses, in the design and analysis of Q690 steel tubes to accurately predict their load-carrying capacity and ensure structural safety.

This figure provides a visual representation of the impact of different imperfection conditions on the critical bending strength of the specimens. It allows for a direct comparison of the simulated bending moments under various scenarios, highlighting the significant influence of residual stresses on the structural response.

F. Local Buckling Test Specimens

Fig. 7 provides crucial insights into the local buckling failure modes observed in the specimens. The stress contour plots vividly illustrate the development and progression of localized deformations, revealing the specific regions where stress concentrations and significant deformations occur.

1. Buckling Patterns: The plots demonstrate distinct buckling patterns, with localized deformation often initiating at specific locations along the tube length. These localized deformations can significantly impact the load-carrying capacity and ultimately lead to structural failure.
2. Influence on Design: The visual representation of the buckling patterns provides valuable information for understanding the failure mechanisms and developing more effective design strategies. By identifying the critical regions prone to buckling, engineers can implement design modifications, such as local reinforcements or changes in cross-sectional geometry, to enhance the structural stability and load-carrying capacity of Q690 steel tubes.

 Fig. 7 Stages of Cement Silo Failure on Steel Structure

This analysis, combined with the numerical simulations and comparisons with existing design codes, provides a comprehensive understanding of the local buckling behavior of Q690 steel tubes under combined loading conditions. These findings have significant implications for the development of improved design guidelines and the optimization of structural performance in practical applications

G. Discussion and Design Recommendations

The experimental and numerical investigations provided valuable insights into the structural behavior of Q690 steel tubes under combined axial compression and bending. Key findings include the significant influence of imperfections on tube performance, the distinct failure modes observed (global instability and local buckling), and the nonlinear relationship between bending moment and axial displacement. While both experimental and numerical methods have limitations, they collectively identified critical failure modes and their dependence on geometric parameters. The inclusion of residual stresses and geometric imperfections in the numerical model significantly improved its accuracy.

Based on these findings, practical design recommendations are proposed, including limits on slenderness and D/t ratios, consideration of imperfection effects, and the adoption of appropriate safety factors. Additionally, updates to existing design codes are recommended to better accommodate Q690 steel, such as adjusting slenderness ratio provisions, revising D/t ratio limits, incorporating imperfection knockdown factors, and including residual stress effects. These recommendations aim to improve the accuracy and reliability of design calculations for Q690 steel tubes.

Conclusion

This study comprehensively investigated the stability and buckling behavior of Q690 high-strength steel cylindrical tubes subjected to combined axial compression and bending. Experimental testing and finite element analysis revealed critical insights into load-bearing capacity, failure modes, and the significant influence of imperfections, such as residual stresses and geometric deviations. Main findings are below: 1) Two distinct failure modes were observed: global instability in tubes with higher slenderness ratios and local buckling in tubes with lower slenderness ratios. 2) Residual stresses significantly reduced critical buckling strength, while geometric imperfections had a more limited impact. 3) Finite element models, incorporating imperfections and material nonlinearities, accurately predicted buckling behavior, with deviations from experimental results within an acceptable range. Based on these findings, practical design recommendations were formulated, addressing limitations in current design codes. These recommendations include: 4) Incorporating the influence of residual stresses and geometric imperfections. 5) Refining slenderness ratio and D/t ratio limits. 6) Adopting appropriate safety factors to account for uncertainties. This research provides a strong foundation for advancing the use of Q690 steel in critical infrastructure. Future research directions include investigating dynamic loading scenarios, exploring hybrid material applications, and developing more sophisticated models for imperfections and material behavior.

References

[1] M. G., \"Definition of High Strength Steel,\" 2017. [2] Steel Construction Institute, \"Steel Construction Manual,\" 2014. [3] A. Dubina, \"Research on weight reduction in steel columns,\" Journal of Structural Engineering, vol. 34, no. 2, pp. 134-142, 2008. [4] Jernkontoret, \"Study on the use of HSS in the Friends Arena stadium,\" 2017. [5] World Steel Association, \"World Steel Production Statistics 2020,\" 2020. [6] L. Johansson and L. Collin, \"Use of S1100 plates in military bridges,\" Journal of Bridge Engineering, vol. 25, no. 1, pp. 45-56, 2005. [7] A. Schroeter, \"Construction of the Millau Viaduct using S460,\" Steel Construction Review, vol. 22, pp. 89-95, 2006. [8] K. Miki, et al., \"The Akashi Kaikyo Bridge: A case study in the use of HSS,\" Bridge Engineering Journal, vol. 16, pp. 200-212, 2002. [9] S. Shi, et al., \"Use of S460 in the Beijing Bird’s Nest Stadium,\" Journal of Structural Design, vol. 32, no. 4, pp. 111-120, 2014. [10] R. Willms, \"Construction of the Freedom Tower with S460,\" Journal of Modern Architecture, vol. 14, pp. 50-61, 2009. [11] Chinese Code for Steel Structures, GB 50017-2003, 2006. [12] Australian Structural Steel Specification, AS 4100-A1, 2012. [13] European Committee for Standardization, Eurocode 3: Design of Steel Structures - Part 1-12, EN 1993-1-12, 2007. [14] Buro Happold Engineering, \"Design of the London Olympic Stadium Roof Replacement,\" 2014. [15] S. G. Ballio and F. M. Mazzolani, \"Residual stresses and their effects on the structural performance of welded elements,\" Welding Journal, vol. 62, no. 5, pp. 154S-160S, 1983. [16] J. A. Goldak and M. Akhlagi, \"Numerical simulation of welding residual stresses,\" Journal of Applied Mechanics, vol. 72, no. 1, pp. 201-212, 2005. [17] L. Lindgren, \"The thermal elasto-plastic analysis of welding and casting,\" Computational Mechanics, vol. 28, no. 3, pp. 167-180, 2001. [18] C. H. Chin, H. S. K., and S. J. C., \"Finite element analysis of welding residual stresses in high-strength steel (HSS) tubular sections,\" Journal of Structural Engineering, vol. 138, no. 4, pp. 477-487, 2012. [19] T. Nishino, S. Horiguchi, and T. Kubo, \"Residual stress distribution in welded structural steel components,\" Welding Research Supplement, vol. 47, no. 2, pp. 99S-108S, 1967. [20] K. J. R. Rasmussen and G. J. Hancock, \"Effects of residual stresses on the stability of welded steel sections,\" Journal of Structural Engineering, vol. 118, no. 6, pp. 1455-1466, 1992. [21] G. Shi, S. Lin, and W. Zhao, \"Residual stress distribution in circular welded steel tubes and their effect on structural stability,\" Journal of Constructional Steel Research, vol. 78, pp. 12-20, 2013. [22] J. G. Teng and J. M. Rotter, \"Imperfections and residual stresses in cylindrical shells,\" in Proceedings of the 2nd International Conference on Structural Stability, 1992, pp. 121-135. [23] Y. Wei, X. Zhang, and H. Jiang, \"Influence of welding residual stresses on axial compressive capacity of cylindrical shells,\" Journal of Thin-Walled Structures, vol. 70, no. 10, pp. 15-26, 2013. [24] C. Yang, W. Li, and Q. Zhao, \"Residual stress distribution in welded high-strength steel tubes: a study on galvanized and non-galvanized tubes,\" Steel Construction, vol. 9, no. 3, pp. 241–249, 2016. [25] F. Wagner, et al., \"Modeling of residual stress distributions in welded tubular sections,\" Journal of Welding Technology, vol. 45, no. 2, pp. 67–73, 1976. [26] W. Chen and J. Ross, \"Residual stresses and their effects in welding of thin-walled structures,\" International Journal of Pressure Vessels and Piping, vol. 5, no. 1, pp. 13-20, 1977. [27] J. M. Rotter, \"Influence of welding residual stresses on the buckling of thin-walled cylindrical shells,\" Journal of Structural Engineering, vol. 122, no. 6, pp. 905-912, 1996. [28] W. T. Koiter, \"The stability of thin-walled shells with geometric imperfections,\" Technical Report No. 45, Delft University of Technology, 1945. [29] D. Bushnell, \"Shell Buckling and Its Applications,\" Journal of Structural Engineering, 1985. [30] L. Lorenz, \"Elastic Buckling of Cylindrical Shells,\" Proceedings of the Royal Society, 1908. [31] S. Timoshenko, \"The Theory of Elastic Stability,\" McGraw-Hill, 1910. [32] R. Southwell, \"The Buckling of Thin-Walled Shells,\" Philosophical Transactions of the Royal Society, 1914. [33] S. Timoshenko and J. Gere, \"Theory of Elastic Stability,\" McGraw-Hill, 1961. [34] E. Riks, \"An Arc-Length Method for Nonlinear Analysis of Shells,\" Journal of Applied Mechanics, vol. 79, no. 2, 1979. [35] W. Flügge, \"Stability of Thin-Walled Shells Under Uniform Load,\" Springer-Verlag, 1932. [36] M. Yamaki, \"Nonlinear Buckling of Cylindrical Shells,\" Journal of Structural Mechanics, 1984. [37] D. Combescure, \"Nonlinear Strain-Displacement Relationships in Shell Buckling,\" Journal of Applied Mechanics, 1986. [38] M. Rotter and A. Jumikis, \"Shell Buckling and Design,\" Elsevier Science Publishing, 1988. [39] E. Rotter, \"Buckling of thin cylindrical shells under axial compression,\" Journal of Structural Engineering, vol. 130, no. 10, pp. 1408-1415, 2004. [40] N. Yamaki, Elastic Stability of Cylindrical Shells, Elsevier Science, 1984. [41] W. T. Koiter, \"A theory of buckling for thin shells,\" Journal of Applied Mechanics, vol. 30, no. 1, pp. 161-172, 1963. [42] C. Speicher and H. Saal, \"Linear buckling analysis of cylindrical shells,\" Journal of Mechanical Design, vol. 113, no. 1, pp. 76-81, 1991. [43] E. Riks, \"Nonlinear analysis of shell structures,\" Journal of Computational Mechanics, vol. 18, no. 2, pp. 121-135, 1996.

Copyright

Copyright © 2025 Shek Rajib, Chen Lei. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.