A Parametric Study on Composite G+8 Structure With Application of Damper on Different Locations Using Time History Analysis

Abstract

The world\'s population has been growing quite quickly in recent years. Major cities, in particular, have relatively dense populations, which has increased demand for new homes. Because there isn\'t enough land for new construction in the majority of the old cities, high-rise buildings are moving into mountainous areas. These days, there is more competition to build high rise buildings all over the world as a result of certain developed nations building extremely tall skyscrapers to demonstrate their power and technology to the rest of the world. Buildings on sloping terrain, however, have different structural configurations than those on level terrain, which causes them to vibrate more during earthquake-induced ground motions, resulting in higher displacements and shears. Increased floor displacement results in damage to the structural components, rendering the structure unusable or, in the worst situation, collapsing as a whole. Reducing the amount of seismic energy that enters slanted ground buildings is essential to preventing damage. This can be done by absorbing the majority of the vibrations that an earthquake produces. There are numerous ways to lessen a structure\'s seismic reaction, including base isolation, shear walls, bracings, dampers, and more. Because of their effectiveness and simplicity of usage, damping devices are particularly well-liked among these methods. The eight-storey building model with four distinct cases—bare frame, bare frame with damper on corners, bare frame with damper on Central Bay, and bare frame with damper on Alternate Bay—is taken into consideration in this research examination. For modeling, use ETABS 2016 Ultimate programme. Utilize time history analysis as well to investigate how earthquake loading affects structures.

Introduction

I. INTRODUCTION

To give dynamic protection to structural systems, vibration control methods in the form of shock and vibration isolators have been designed. Fluid-viscous dampers, for example, have been shown to have desirable performance in controlling shock loads. Fluid viscous dampers are appealing for improving performance since they minimize not only the deformation demand but also the force delivered to the structure as a result of energy dissipation.

Traditional linear fluid-viscous dampers can only dissipate a limited amount of energy and are not as effective for shock loads as nonlinear dampers (Narkhede, D. I., and R. Sinha. 2012)1. For reducing structural resonance, viscous damping is a beneficial energy dissipation technique. A "turbulent viscous damper" (damper) functions by forcing a low-viscosity fluid through microscopic pores, while a "lamellar viscosity unit" (damper) works by forcing a high-viscosity fluid between moving objects. This is accomplished through fluid transfer. Dilution The first is commonly utilized in the manufacture of shock absorbers for car suspensions. "Viscous turbulent dampers" (damper-type dampers) are multidirectional, have a complex mechanical design, and must be maintained on a regular basis, whereas "laminar viscous dampers" (dampers) are multidirectional, have a simple mechanical design, and must be maintained.

A. Application of Damper

Dampers are intelligently positioned in the structure of the building to regulate floor vibrations and building displacement, cater to occupant comfort and mitigate against significant seismic events. The dampers capture the energy produced by building displacement and floor vibration, and then release it as heat energy. Even during an earthquake, the building's inhabitants will suffer less floor vibration, smaller building displacements, and overall better occupancy comfort (Lee, David, and Martin Ng, 2010)16.

B. Presently Fluid Viscous Damper Applied

The technology was first brought to China on the Chongqing Egongyan Yangtze River Bridge in 2000 and is now widely used in Yangtze River bridges. Viscous dampers have been used in the last 30 years in major civil structures to mitigate the effects of earthquakes.

Their use in high-rise buildings built in seismic areas is a challenge for the designers, since they should reduce the vibrations induced by both strong winds and earthquakes, and the optimal behaviour in these two situations is not usually the same. Consequently, the design requirement for viscous dampers to be used in high-rise buildings is often that they should have two different behaviour in the different range of velocities corresponding to wind and earthquake. Recently Viscous Damper with said behaviour has been applied in three high-rise buildings in Asia, the St. Francis Twin Towers in Manila, the Philippines, and Taipei 101 in Taipei, Taiwan.

C. Types of Fluid Viscous Damper

1. Turbulent Flow (Shock Absorber Type) Viscous Damping Devices
2. Laminar Flow Viscous Dampers (Dashpots)

D. Time History Analysis

A dynamic analysis technique is code time history analysis. It could be linear or not. This is a step-by-step investigation of the dynamic response of a structure to particular time-varying stresses (Patsialis et.al, 2022)1. Direct integration techniques or fast nonlinear (FNA) techniques can be used for this. The motion equations are integrated over a period of time using the direct integration method. A modal analysis technique is FNA.

E. Non-Linear Time History Analysis

The bridge is analyzed for actual ground vibrations in non-linear analysis. In this analysis, non-linarites in the member will be specifically described. Using this technique, it is possible to determine whether the structure's strength is sufficient to handle the anticipated inelastic deformation. The sub-structure has been subjected to a non-linear analysis using three time histories that are MCE-compliant.

II. PROBLEM STATEMENT

1. To get knowledge about effect of composite structure with application of damper on different locations using time history analysis consider as research problem.
2. A lot of work done with dampers but analysis of damper with time history not done yet. Also provide the most appropriate site damper in model based on the current conditions by comparing various seismic characteristics.
3. Composite structure system which optimizes economy, serviceability, construction time and seismic performance may be considered as optimum structural system. Study dampers characteristics through the analysis of nine storey building.
4. Generally to achieve the objectives of constructions in economical way, composite structure design and construction technology plays enormous role.
5. Developing countries has to give especial attention to get its benefit. Specifically, the India is one of the developing countries, and its economy is developing rapidly. Thus, this construction technology contributes a lot in the current context of the country to answer the demand of economical designs.

III. OBJECTIVES

1. Due to the load combination of the dead load and seismic load, storey drift, drift ratio, and shear forces occur to limit joint displacement.
2. To study the damper & time history analysis using software.
3. Prepared different composite building models for different zone V and IV.
4. Compare the model parameters and discusses result like joint displacement, storey drift, drift ratio, shear force and bending moment.
5. To compare bracing's impact on composite structures.

IV. METHODOLOGY

In this section we study on 8 storey building model with four different cases like model with bare frame, bare frame with damper on corners, bare frame with damper on Central bay and bare frame with damper on Alternate Bay. We use ETABS 2016 Ultimate software for modeling.

Model Geometry

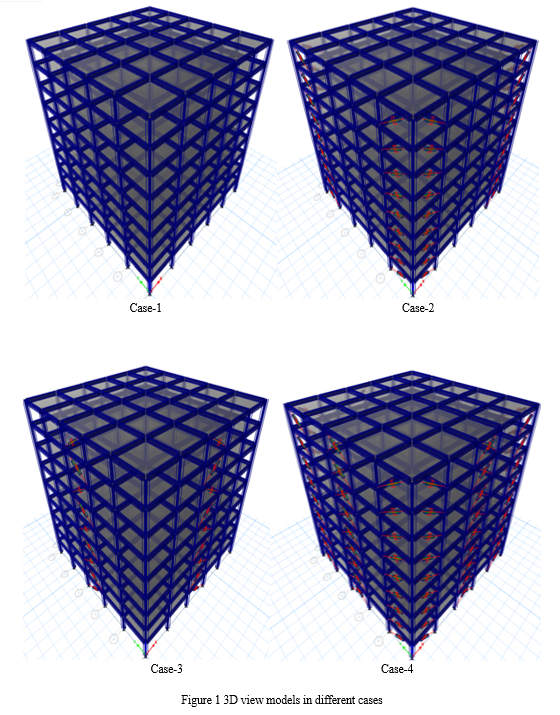
Conclusion

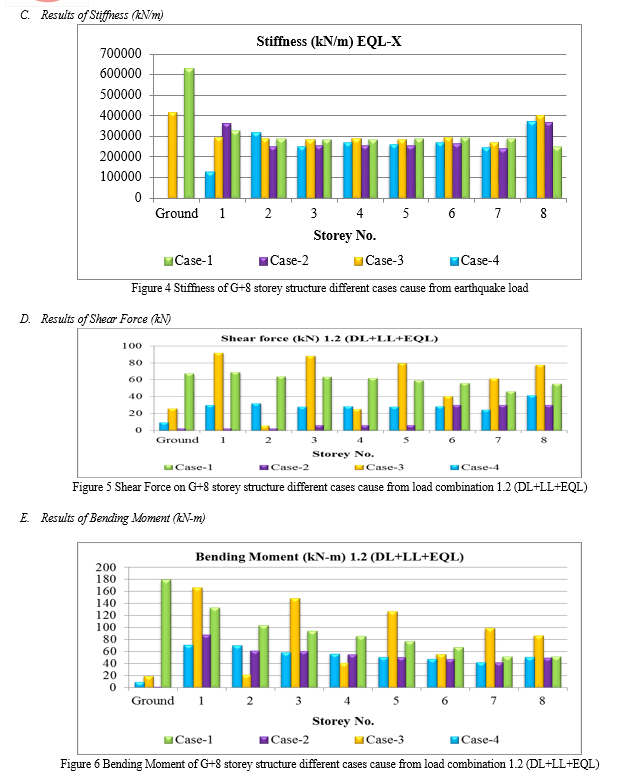
1) In the bare frame value of joint displacement was 60.83mm at top floor. When damper applied on corner this joint displacement was 33.35mm decreased. Location of damper was at centre then joint displacement was 44.04mm. And finally location of damper placed at alternate bays then joint displacement was 30.18mm. 2) It is noticed that maximum change in joint displacement happen in case-4 when dampers were placed at alternate bays and minimum reduction happen in case-3 when damper were placed at centre. 3) In the bare frame value of storey drift was 0.001009 at top floor. When damper applied on corner this storey drift was 0.00173 increased. Location of damper was at centre then storey drift was 0.001935. And finally location of damper placed at alternate bays then storey drift was 0.001626. 4) It is noticed that maximum change in storey drift happen in case-3 when dampers were placed at centre and minimum reduction happen in case-4 when damper were placed at alternate bay. 5) In the bare frame value of stiffness was 243861.96kN/m at top floor. When damper applied on corner this stiffness was 362349.59kN/m increased. Location of damper was at centre then bending moment was 397611.43kN/m. And finally location of damper placed at alternate bays then stiffness was 367889.78kN/m. 6) It is noticed that maximum change in stiffness happen in case-3 when dampers were placed at centre and minimum reduction happen in case-2 when damper were placed at centre. 7) In the bare frame value of shear force was 54.441kN at top floor. When damper applied on corner this shear force was 29.3043kN decreased. Location of damper was at centre then shear force was 76.926kN. And finally location of damper placed at alternate bays then shear force was 40.538kN. 8) It is noticed that maximum change in shear force happen in case-3 when dampers were placed at centre and minimum reduction happen in case-4 when damper were placed at alternate bay. 9) In the bare frame value of bending moment was 50.77kN-m at top floor. When damper applied on corner this bending moment was 49.05kN-m decreased. Location of damper was at centre then bending moment was 85.98kN-m. And finally location of damper placed at alternate bays then bending moment was 49.75kN-m. 10) It is noticed that maximum change in bending moment happen in case-3 when dampers were placed at centre and minimum reduction happen in case-4 when damper were placed at alternate bay. 11) In the bare frame value of base reaction was 3400.9667kN. When damper applied on corner this bending moment was 2340.9323decreased. Location of damper was at centre then bending moment was 3161.7707kN. And finally location of damper placed at alternate bays then bending moment was 716.8096kN. 12) It is noticed that maximum change in bending moment happen in case-3 when dampers were placed at centre and minimum reduction happen in case-4 when damper were placed at alternate bay.

References

[1] Kontoni, D.P.N. and Farghaly, A.A., 2023. Enhancing the earthquake resistance of RC and steel high-rise buildings by bracings, shear walls and TMDs considering SSI. Asian Journal of Civil Engineering, pp. 1-14. [2] Kontoni, D.P.N. and Farghaly, A.A., 2023. Seismic control of T-shape in plan steel high-rise buildings with SSI effect using tuned mass dampers. Asian Journal of Civil Engineering, pp. 1-15. [3] Ding, Y., Zhou, Z., Huang, L. and Si, Y., 2021. Seismic performance of self-centering glulam frame with friction damper. Engineering Structures, 245, p. 112857. [4] Patsialis, Dimitrios, and Alexandros A. Taflanidis. \"Implementation of Reduced-Order Modeling for Time History Analysis of Hysteretic Structures Equipped with Seismic Protective Devices.\" Journal of Structural Engineering 148.11 (2022): 06022004. [5] Ajay, Lingala, and M. Anil Kumar. \"Torsional Vibration Control of a Structure using Fluid Viscous Dampers.\" IOP Conference Series: Materials Science and Engineering. Vol. 1197, No. 1. IOP Publishing, 2021. [6] Manchalwar, A. and Bakre, S.V., 2020. Vibration control of structure by top base isolated storey as tuned mass damper. International Journal of Dynamics and Control, 8(3), pp. 963-972. [7] Liu, Y., Wang, K., Mercan, O., Chen, H. and Tan, P., 2020. Experimental and numerical studies on the optimal design of tuned mass dampers for vibration control of high-rise structures. Engineering Structures, 211, p. 110486. [8] Deringöl, Ahmet Hilmi, and Esra Mete Güneyisi. \"Influence of nonlinear fluid viscous dampers in controlling the seismic response of the base-isolated buildings.\" Structures. Vol. 34. Elsevier, 2021. [9] Ahiwale, Dhiraj, et al. \"Seismic response assessment of steel frame step-back building for different fluid viscous dampers.\" Journal of Seybold Report ISSN No 1533 (2020): 9211. [10] Taipicuri, Y., C. Zavala, and L. Nuñez. \"Experimental Study of a Recycled Prototype of A Real Scale Fluid Viscous Damper.\" 2020 [11] Shen, Dejian, and Soheila Kookalani. \"Effect of Fluid Viscous Damper parameters on the seismic performance.\" Journal of Civil Engineering and Materials Application 4.3 (2020): 141-153. [12] Subasini, Y., and C.G. Sivakumar. \"Analytical study on seismic response of RC and steel structures with fluid viscous dampers.\" IOP Conference Series: Materials Science and Engineering. Vol. 989, No. 1. IOP Publishing, 2020. [13] Shariati, A., R. Kamgar, and R. Rahgozar. \"Optimum layout of nonlinear fluid viscous damper for improvement the responses of tall buildings.\" Int J Optim Civil Eng 10.3 (2020): 411-431. [14] Moradpour, S., and M. Dehestani. \"Optimal DDBD procedure for designing steel structures with nonlinear fluid viscous dampers.\" Structures. Vol. 22. Elsevier, 2019. [15] Mujeeb, Md, J.S.R. Prasad, and Venu Malagavelli. \"Performance of Fluid Viscous Dampers on Seismic Response of RCC Structures.\" International Journal of Innovative Technology and Exploring Engineering 8.12 (2019): 2453-2459. [16] Sahu, Gitanjali, and Pukhraj Sahu. \"Comparative analysis of effects of base isolator & fluid viscous damper on response of a RCC structure.\" International Research Journal of Engineering and Technology 6 (2019): 94-101. [17] Kuckian, Sachin, et al. A study on seismic response of reinforced structures retrofitted with fluid viscous dampers in shear walls. GRIN Verlag, 2019. [18] Constantinou, Michalakis C., and M.D. Symans. Experimental and analytical investigation of seismic response of structures with supplemental fluid viscous dampers. Buffalo, NY: National Center for earthquake engineering research, 1992. [19] Zhao, Yue, et al. \"Influence of fluid viscous damper on the dynamic response of suspension bridge under random traffic load.\" Advances in Civil Engineering 2020 (2020): 1-19. [20] Lee, David, and Martin Ng. \"Application of Tuned Liquid Dampers for the Efficient Structural Design of Slender Tall Buildings.\" CTBUH Journal (2010): 30-36. [21] Sadeghi, Jamal. (2018). modeling moving solid in fluid volume in comsol. [22] Guo, Tong, et al. \"Seismic upgrade of existing buildings with fluid viscous dampers: Design methodologies and case study.\" Journal of Performance of Constructed Facilities 29.6 (2015): 04014175. [23] Fluid Viscous Dampers for Buildings and Bridges | Seismic Dampers | Taylor Devices, Inc. [WWW Document], n. d. URLhttps://www.taylordevices.com/products/fluid-viscous-dampers/

Copyright

Copyright © 2024 Omika Kandare, Ms Deepa Telang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.