Design of a Hybrid Excitation Controller for Multimachine Infinite Bus Power System

Abstract

A significant portion of contemporary power networks is still conventional power system that uses synchronous generators to produce electricity. Conventional power systems are operated under various operating situations by means of excitation systems and turbine-governor systems of synchronous generators. This paper proposes an excitation controller for synchronous generators (SGs) in a multi machine infinite bus (MMIB) power system through combining the idea of the nonlinear backstepping (BS) and partial feedback linearization methods. The model of third-order has been linearized into a second-order linearized system that is independent of the rotor angle which is unmeasurable, using the partial feedback linearization approach. In this case, the BS is applied to the partially linearized system. The idea is to find a control input that drives the system towards a desired behaviour while ensuring the transformed states converge to their target values. Lastly, simulation research is carried out on an MMIB system to analyse how the proposed control mechanism (BS-PFLC) performs in stabilizing the system under a three phase-to-ground fault conditions of power networks. To demonstrate the effectiveness of the BS-PFLC, an existing excitation controller has been used to compare the performance.

Introduction

I. INTRODUCTION

Transient stability is among the most difficult and critical aspects of modern power networks. Transient stability means the capability of a power network to get back to a stable operating condition after being exposed to three-phase faults, line-to-line faults, line-to-ground faults, sudden loss of large generator, sudden load changes etc. Synchronous generators play a major role to increase the frequency and voltage stability and supply majority of load demands in modern power systems. To enhance the transient and dynamic stability of power networks, the excitation control of synchronous generators is considered as one of the most economic and effective methods. In power networks where the primary control goal is to introduce more damping to the system to increase the stability, power systems stabilizers (PSSs) are typically employed to alter the signals used for excitation control [1]. However, the primary purpose of these PSSs is to remove low-frequency oscillations brought on by minute disruptions (such as minute changes in load demands). Furthermore, when power systems experience significant disruptions, such as abrupt short-circuit faults or significant variations in load demands, they are unable to offer sufficient damping. To overcome the drawbacks of these PSS based controllers, an advanced level linear controller like, linear quadratic regulator (LQR) is proposed in [2]. However, this linear excitation controller is unable to preserve the system stability under large disturbances like three-line to ground faults and it can perform only over a fixed operation point set. During such conditions, nonlinear excitation controllers that use techniques like sliding mode control, feedback linearization and adaptive backstepping offer significant advantages in terms of stability, robustness, and flexibility in handling dynamic and nonlinear behaviours of power systems [3].

Feedback linearization procedure is often utilized in power systems to improve the transient stability, which is critical for maintaining system reliability during disturbances. This approach can be classified into exact feedback linearization (EFL), partial feedback linearization (PFL) and direct feedback linearization (DFL) according to the existing literature. The major drawback of the EFL and DFL techniques is that, the inestimable rotor angle is taken into consideration as an output function [4]. On the contrary, the PFL technique considers speed deviation as the output function that can be directly measured and thus it can outperform the previous techniques [5]. Though these feedback linearizing controllers are able to boost the stability of power networks but they show sensitivity towards parametric variations. Sliding Mode Control (SMC) is often seen as a strong alternative to Feedback Linearization (FL) methods, especially due to its robustness. Unlike FL, SMC can handle external disturbances and system uncertainties effectively, which makes it particularly valuable in applications where the system may face unpredictable variations or noises [6]. But these Sliding Mode Controllers exhibit unexpected chattering problem. A hybrid controller using partial feedback and backstepping has been proposed in [7] but they considered a SMIB system which was unable to eliminate the disturbances related to multimachine systems.

To address the disadvantage, a Backstepping (BS) method can be employed as an alternative approach, especially for designing an excitation controller for Synchronous Generators (SGs) [8]. This paper proposes a hybrid control scheme that leverages the strengths of the Backstepping (BS) control technique. This approach aims to improve power system transient stability while overcoming the parametric sensitivity associated with the Partial Feedback Linearization (PFL) method.

The major objective of this paper is to establish a controller for the SGs in a MMIB power network. In this procedure, a hybrid nonlinear controller has been designed by integrating the Partial Feedback Linearization (PFL) technique with the Backstepping (BS) control method. Firstly, the nonlinear dynamic model of the system is partially linearized using the PFL technique. This simplifies certain nonlinear aspects of the system. After partial linearization, the BS formula is applied to create the excitation control signal. To ensure stability, the Control Lyapunov Function (CLF) method is implemented which verifies stability at each step of the design. The hybrid controller is implemented in MATLAB/Simulink to test its performance across various operating conditions, providing a practical assessment of its effectiveness. Finally, the performance of an existing controller, like power system stabilizers (PSSs), is contrasted with that of the suggested controller.

Fig. 1  4-machine, two-area, 11-bus test power network

II. SYSTEM MODELLING AND PARTIAL FEEDBACK LINEARIZATION

In this section, the model details of synchronous generators in a MMIB power network as illustrated in Fig. 1. The accuracy of the dynamic model for each element in a power network is crucial for effective controller design. A multimachine power system can be viewed as an interconnected network of several Single Machine Infinite Bus (SMIB) systems. Each generator within the system can be analysed as an SMIB system, where it interacts with other generators through transmission lines, transformers, and loads, ultimately forming a complex and interconnected power grid. For N numbers of SGs in a MMIB network, an ith synchronous generator's dynamics can be precisely modeled as a SMIB system, i.e. in a MMIB power network the synchronous generator can be depicted by a model of third-order, where the last order is electrical dynamics and the first two are mechanical dynamics [8].

In a MMIB power network, the mechanical dynamics of ith SG can be expressed as:

                                     (1)

here i = 1, 2, 3,4,…..N, the ith  SG’s rotor speed is , is the ith SG’s rotor angle,  is the ith SG’s constant of inertia,  is the ith SG’s synchronous speed,  is the ith SG’s mechanical power input,  is the ith SG’s constant of damping, and  is the  ith SG’s delivered active power.

In a MMIB power network, the mechanical dynamics of ith SG might be symbolized as:

                                                                      (2)

where is the ith SG’s transient voltage of quadrature-axis, is the ith SG’s voltage of quadrature-axis, is the ith SG’s open-circuit time constant of direct-axis, and the corresponding voltage in the excitation coil of ith SG is .

Like an SMIB system, some of the equations are algebraic for MMIB power networks and those can be expressed using the following equations that determine the steady-state properties:

                                  (3)

here  is the synchronous reactance for direct-axis of ith SG,  is the ith SG’s transient reactance of direct-axis,  and  are the self-susceptance and self-conductance of ith bus correspondingly,  and  are the susceptance and conductance between ith and jth buses correspondingly, =  is the deviation of power angle between ith and jth buses, and  are quadrature and direct-axis currents of ith SG, correspondingly,  is the reactive power produced by ith SG, and  is the terminal voltage of ith SG’s terminal voltage.

It is possible to employ these algebraic equations with the differential equations in (1) and (2) and by performing this, equations (1) and (2) can be represented as:

                                                      (4)

The equation (4)   symbolizes the entire dynamical model of ith SG in a MMIB power system. This system may be represented

as,

                                                                                           (5)

                                                                                           (6)

 Here,

                        (7)

                       and                           (8)

The variance in speed is regarded as the output function here. So, the nonlinear systems symbolized by equations (5) and (6) is partially linearized that can be shown as,

                                                                                                                      (9)

                                                                    (10)

where,

Considering the equations (9) and (10) the proposed hybrid controller is developed which are foresighted during the next  section.

III. DESIGN OF PROPOSED HYBRID EXCITATION CONTROLLER

The nonlinear backstepping partial feedback linearized controller (BS-PFLC), a design method for the upcoming hybrid excitation controller, is demonstrated to acquire the input that regulates the system of excitation. The subsequent steps in the detailed design process, are presented in an ostentatious manner.

A. Step 1:

In order to achieve the design procedure's goal, the first variable of error could be defined as follows:

                                                                                      (11)

Here, the state’s standard value is . Employing equation (9), the dynamic of equation (11) can be represented as,

                                                                    (12)

The stability analysis of  is crucial at this point, and the stabilizing function for it is . The initial Lyapunov function

(LF) for this purpose can be expressed as,

                                                                                               (13)

By employing the value of , the dynamic of equation (13) can be composed as,

                                                         (14)

At this point, the system is asymptotically stable, meaning that , by selecting the relieving function  in a way

that . Consequently,

                                                               (15)

Where, a constant is  that is positive. Equation (15) is inserted into equation (14) to produce,

                                                                                         (16)

B. Step 2:

Since  is a virtual control variable, the definition of another error is,

                                                                       (17)

The error dynamic  can be represented in the following manner,

                                                           (18)

Equation (18) contains the actual excitation control input , which will choose such that the errors  and  will approach

to zero as time reaches infinity. For the attainment of such a control goal, the final CLF is regarded as,

                                                              (19)

Using equations (16) and (19), the time derivative of  is,

                (20)

In order to ensure system stability, the following requirements must be met:

                                                                                               (21)

If the input from the equation (20) for the excitation control is constructed as follows, the condition shown by equation (21) will

hold:

                                          (22)

where, another constant is . Utilizing equation (22), equation (20) can be expressed as,

                                                               (23)

It is evident from equation (23) that , indicating the overall system's asymptotic stability. The following section  presents the simulation results on the basis of this developed control input.

IV. SIMULATION OUTCOMES

In this section, a similar MMIB power system, as shown in Fig. 1, is used to validate the designed controller performance using MATLAB/Simulink program. The system's nominal values utilized in the simulation are shown as follows:

TABLE I

Parameters of Multimachine Power Network

To evaluate the controller performance, a three-line to ground fault has been applied at the transmission line-1, between bus-7 and bus-8. This fault is applied at t=1s and dismissed at t=1.2s throughout this paper. This time is generally considered a huge duration for any power network. The performance of the developed excitation controller has been compared to an existing one in order to demonstrate its superiority.

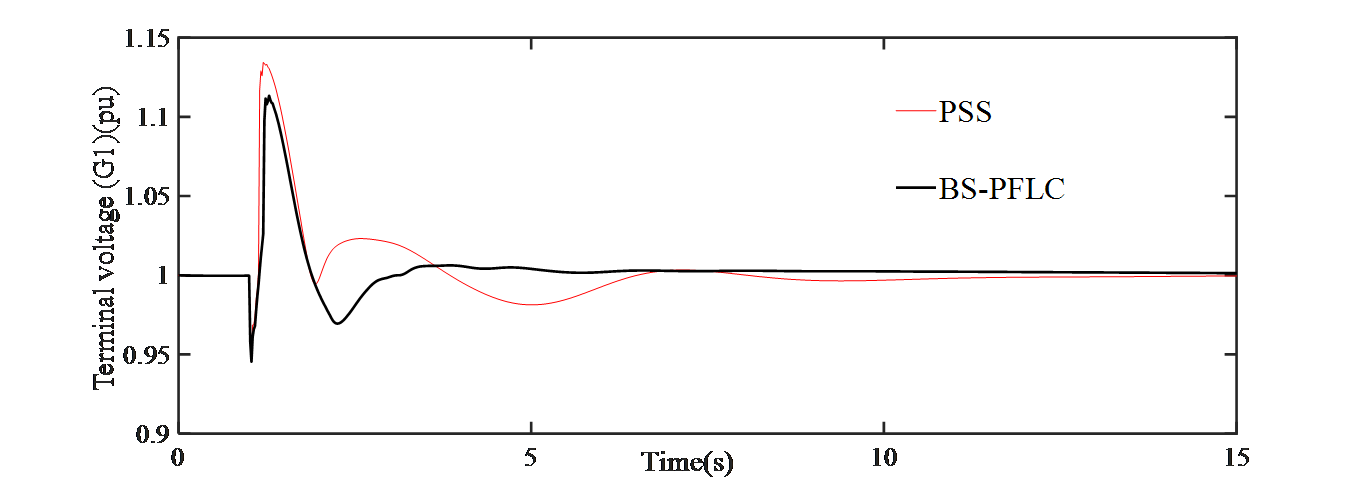
1. Generator SG1

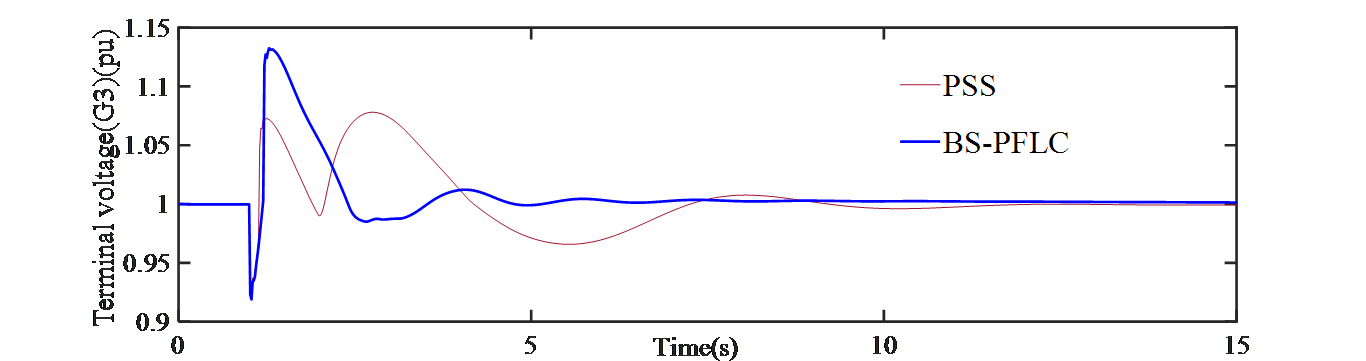
1. Generator SG3

Fig. 2: Terminal voltages of SGs when line-1 is permanently tripped

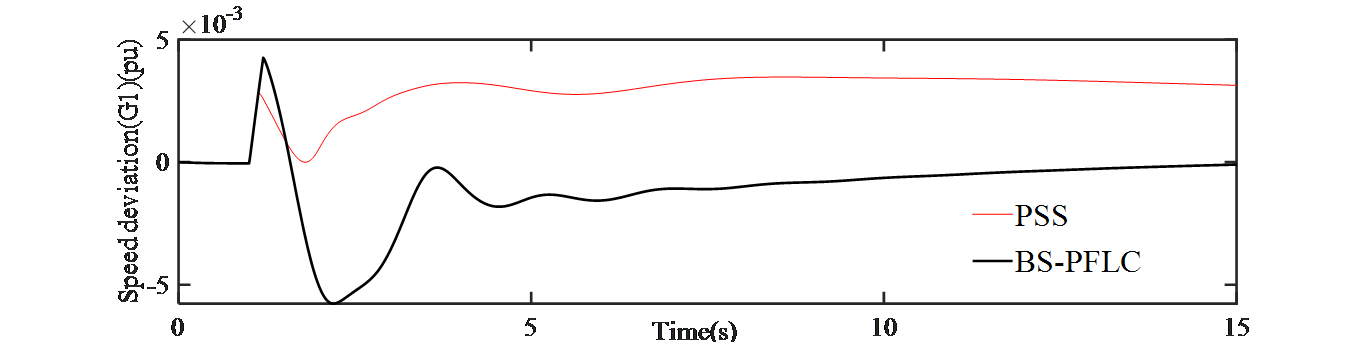
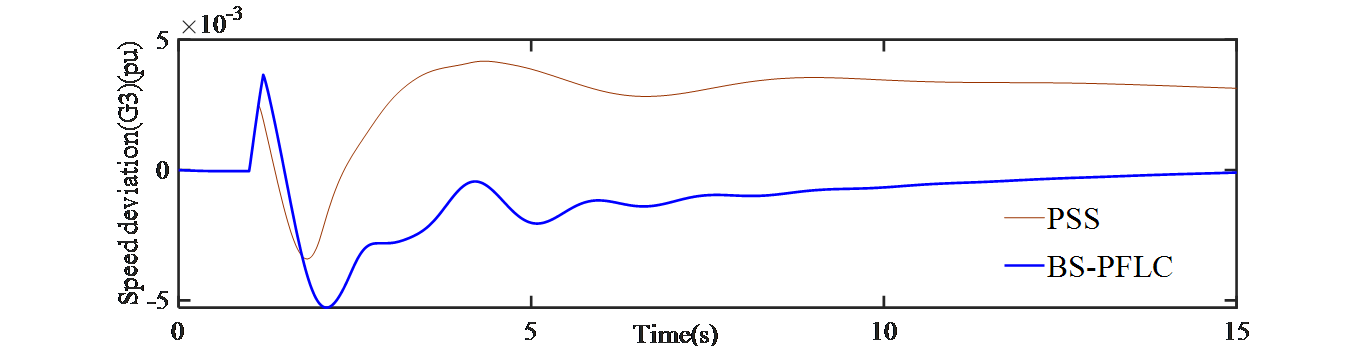
(a) Generator SG1                                                                            (b) Generator SG3

Fig. 3: Speed deviations of SGs when line-1 is permanently tripped

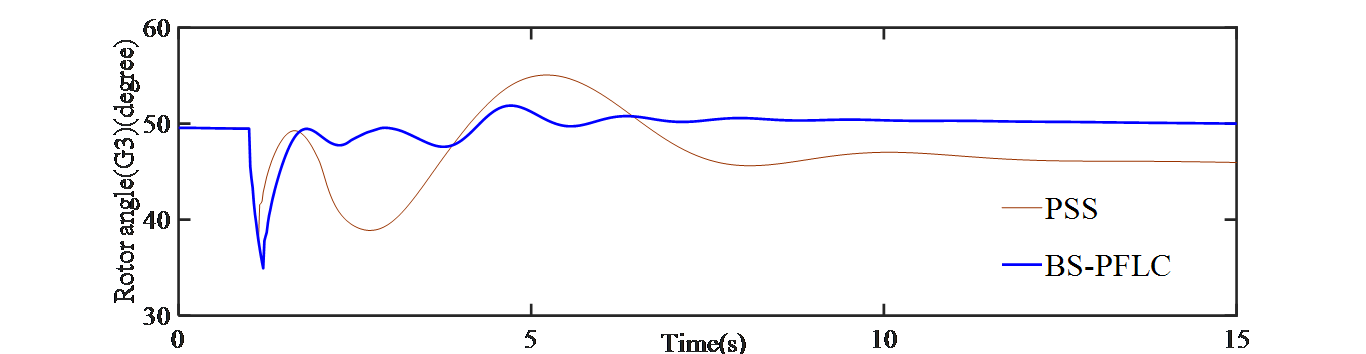
(a) Generator SG1                                                                           (b) Generator SG3

Fig. 4: Rotor angles of SGs when line-1 is permanently tripped

For comparison purpose, the designed controller is applied at the synchronous generator-1 (SG-1) which is located on area-1  and on the synchronous generator -3 (SG-3) which is located on area-2 of Fig. 1. It is observed from Fig. 2 that, the designed BS-PFLC outperforms the conventional PSS in terms of overshoot and settling time. Again, the speed deviation of generator 1 is shown in Fig. 3(a) and for generator 3 is shown in Fig. 3(b). It is observed that the designed BS-PFLC can tackle the effect of three phase-fault in an effective manner and consequently the deviation in speed is minimized since it is very important to keep the deviation in speed zero under typical operating circumstances. The rotor angle for SG-1 and SG-3 is shown in Fig. 4(a) and  Fig. 4(b) respectively. It is evident from the results that the designed hybrid controller stabilizes the rotor angle in an efficient way than that of the PSS.

Conclusion

This paper mainly introduces a hybrid excitation controller for a third-order dynamical model-based SG to improve the transient stability of a multimachine power network. Using the nonlinear feedback linearization method, a model of decreased order is produced in order to construct the suggested controller while eliminating the nonlinear elements. Through simulation analysis, it is shown that the hybrid excitation controller clearly demonstrates support for the theoretical design in terms of supplying extra dampening in the event of a major three phase fault malfunction at the generators ends. A comparative simulation analysis is presented to demonstrate the utility of the BS-PFLC over the PSS. Consequently, it can be concluded that the BS-PFLC design can enhance the multimachine power network\'s transient stability. For future studies, a hybrid controller can be designed which can handle both external and model uncertainties.

References

[1] J. Y. Fan, T. H. Ortmeyer, and R. Mukundan, “Power system stability improvement with multivariable self-tuning control,” IEEE Transactions on Power Systems, vol. 5, no. 1, pp. 227–234, February 1990. [2] M. J. Hossain, H. R. Pota, V. A. Ugrinovskii, and R. A. Ramos, “Voltage mode stabilization in power systems with dynamic loads,” Int. Journal Elect. & Power Eng. Syst., vol. 32, no. 9, pp. 911-920, November 2010. [3] B. Fan, Q. Yang, K. Wang, J. Xu, and Y. Sun, “Transient stability enhancement control of power system with time varying constraints,” IET Generation,Trans. & Distribution, vol. 10, no. 13, pp. 3251–3263, 2016. [4] A. Kazemi, M. R. J. Motlagh, and A. H. Naghshbanddy, “Application of a new Multi-variable feedback linearization method for improvement of power systems transient stability,” Int. Journal of Elect. & Power Eng. Systems, vol. 29, no. 4, pp. 322-328, May 2007. [5] T. Roy, M. A. Mahmud, A. Oo, H. R. Pota, “Nonlinear Adaptive Backstepping Excitation Controller Design for Higher-Order Models of Synchronous Generators,” IFAC-Papers On-line, vol. 50, issue 1, pp. 4368-4373, 2017. [6] T. K. Roy, M. Mahmud, M. A. Barik, A. B. M. Nasiruzzaman, A. Oo, “A Nonlinear Backstepping Control Scheme for Rapid Earth Fault Current Limiters in Resonant Grounded Power Distribution Systems: Applications for Mitigating Powerline Bushfires,” Early Access (2021), DOI: 10.1109/JESTIE.2021.3088387. [7] T. S. Joyeeta, T. K. Roy and M. R. I. Sheikh, “Design of a Nonlinear Excitation Controller for Single Machine Infinite Bus Power Systems to Improve the Transient Stability,” Int. Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), 2021, pp.1-5. [8] T. K. Roy, M. A. Mahmud and A. M. T. Oo, “Robust Adaptive Backstepping Excitation Controller Design for Higher-Order Models of Synchronous Generators in Multimachine Power Systems,” IEEE Trans. on Power Systems, vol. 34, no. 1, pp. 40-51, Jan. 2019.

Copyright

Copyright © 2024 Tasnim Sarker Joyeeta. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.