Design of Power Optimised Truncated Approximate Booth Multiplier

Abstract

In digital signal processing and arithmetic circuits, Booth multipliers are widely used for efficient multiplication of signed numbers. However, conventional Booth multipliers consume significant power due to their full precision operation. This paper explores efficient approximation techniques for Booth multipliers enhanced with flip-flop clock gating to reduce power consumption. Booth multipliers traditionally consume significant power due to their full precision operations. In this approach it mainly focuses on truncating less significant bits in the Booth encoding to lower computational demands without compromising performance. Additionally, flip-flop clock gating dynamically disables clock signals to idle flip-flops during non-active computation phases, further reducing power dissipation. Simulation results demonstrate substantial power savings compared to conventional Booth multipliers while maintaining acceptable accuracy for digital signal processing applications. These findings contribute to advancing energy-efficient arithmetic units, particularly beneficial for battery-powered devices and embedded systems where power efficiency is crucial.

Introduction

I. INTRODUCTION

We are aware that multipliers are used in all fundamental circuits. Today, multipliers are the foundation of every ALU system. The entire logical portion of complete arithmetic is predicated on a multiplier, and if the multiplier is taking too long, the entire product that is based on the multiplier will fail since the multiplier failed. A multiplier will operate slowly if its speed is low. Regarding this, if our function takes two seconds to complete, there will be a delay. The output then has a delay of at least two seconds. That delay could be longer than the standard performance delay

In VLSI, power consumption, area, and latency all affect an IC's speed. When a circuit is complicated, there will be an increase in power consumption and latency. Another important power element is power usage. If we lower an IC's power factor, it indicates that the battery life of our device is good. Everyone uses computers and calculators today. Every manufacturer strives to develop low power consumption circuits in order to supply batteries with longer lives than their competitors Heat dissipation will increase as our multiplier's power consumption rises. As a result, leakage current will rise. In many ALU circuits, this multiplier will thus be employed. Then all these ALU's products have a short battery life. The battery of a mobile phone will not last as long if the

memory allocation is done by multiplier operations since the heat dissipation and power consumption are above average. In accordance with "Moore's Law", everyone and Half Year, an IC's transistor count will double.

According to Moore Low, we shall receive a new IC (integrated circuit) every One and half year that contains a greater number of transistors than the preceding one. We now wonder what advantages this increase in transistors will bring about. The functionality of the transistor must be increased as the number of transistors increases. In compared to earlier IC, our current IC can function faster and more efficiently.

A. Booth Multiplier

Both signed and unsigned bits can be multiplied using the fundamental booth multiplier. When using this multiplier shifting operation, some cases use the direct method and others use the 2's complement. Therefore, it is one of the intricate processes where each bit is examined before shifting occurs during multiplication. The block diagram is shown in Fig 1.

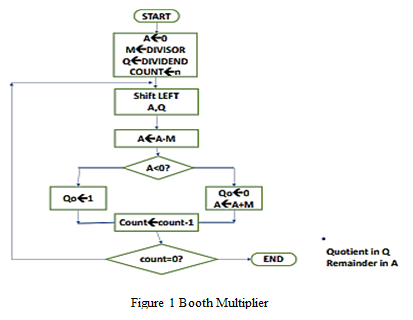
The end outcome happens when the sequence counter approaches zero. As a result, it is one of the lengthiest processes to complete and takes a long time. As a result of this drawback, the delay also grows and gradually leads to its increment, which subsequently slows the multiplier's speed. Power usage also rises as a result. We choose the adjusted booth multiplier after taking all these disadvantages into account. When utilising a booth multiplier to do the multiplication, the number of iteration steps will be decreased. There are four components to the architecture: Booth Encoder, Partial Product, Carry Save Adder, and Complement Generator. The flow chart is shown in Fig 2.

B. Encoder

The beginning bits are supplied to the encoder in order to do the multiplication, followed by the applied bits of the encoder being regarded as one bit for the two bits, and lastly the multiplication is performed for the bits.

C. Partial Product Generator

Less partial products are produced while multiplying integers thanks to the decoded bits, which are gained at the partial product generator. As a result, there are fewer incomplete goods produced.

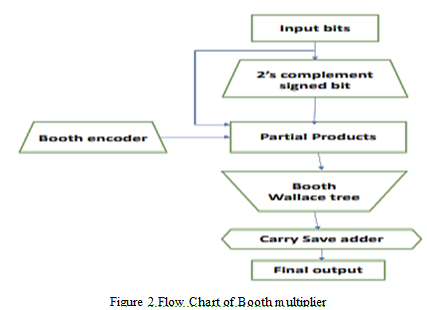
D. Carry save adder

This adder is said to be superior to other adders since it performs the quick adding of the partial products and produces the result so quickly. The Booth multiplier, which has fewer steps while doing addition than conventional multiplication, detects the operand that serves as a multiplier and may perform multiplication for the method. When multiplying, the operation is carried out for each bit of the multiplier and the multiplicand, after which the partial products are generated in the appropriate sequence and added together. The most intriguing aspect is that this method is excellent since the additions carried out during the multiplication are data dependant.

E. Complement Comparator

When using this complement comparator, the multiplicand or the supplied data are used to generate the 2's complement, and then the complemented results are produced. When necessary, these supplemented findings are employed; otherwise, the direct result is considered in specific circumstances because of specified predetermined circumstances.

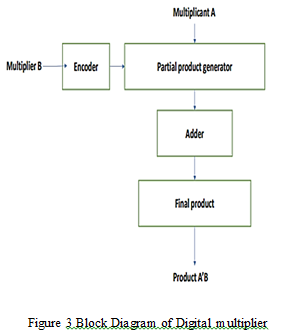
The partial products creation, compression, and final summation steps make up a binary multiplier. The effectiveness of the overall multiplier design is mostly determined by the Booth encoding technique, which is frequently incorporated into the first step and significantly lowers the number of partial products produced. In order to further reduce hardware, an approximation of the Booth method has been constructed.

II. LITERATURE SURVEY

Truncated Booth multipliers using approximate compressors, while enhancing performance and reducing area, face several drawbacks. The primary issue is the trade-off between accuracy and efficiency; the approximation methods can introduce significant errors in the final results, affecting the reliability of computations. Additionally, the truncation process can lead to increased quantization noise, which impacts precision. This can be problematic in applications requiring high accuracy, such as digital signal processing. Designing and validating these circuits is complex, requiring careful analysis and extensive testing, which increases design effort and time. Moreover, such systems can be complex, requiring careful consideration of error propagation and mitigation strategies. The balance between speed, area, and accuracy remains a critical challenge in these designs.   Paper1https://ieeexplore.ieee.org/document/10112910/

III. EXISTING METHOD

An around radix-256 Booth encoding is suggested using a partial encoding strategy that makes use of carefully chosen partial product pairings to tackle challenging multiple difficulties and achieve a low error distance. This Booth encoding-based multiplier design displays an improved performance-accuracy trade off. Simulation Outcome for Partial Product Generation on Radix 256 Booth Encoding & approximate Summation Unit, Design of the Booth Multiplier using Verilog HDL and Analysis of Area, time, and power using Xilinx. RTL Schematic View of Booth Multiplier seen in a Xilinx tool the proposed booth multiplier is compared to the traditional booth multiplier and its decrease of the area in terms of slices, gates, and LUT. Gate and path delays are being reduced. It decreases in both static and dynamic power.

A. Radix-256 Booth Encoding

In a radix-256 Booth encoding scheme, the multiplicand and multiplier are segmented into groups of 8 bits. Each group is encoded using a radix-256 code, which efficiently handles the multiplication process by reducing the number of partial products compared to traditional Booth encoding. This reduction is achieved by pairing carefully selected bits within each group, leveraging the properties of radix-256 to minimize the computational overhead.

B. Partial Encoding Strategy

The partial encoding strategy within radix-256 Booth encoding involves selecting specific pairs of bits within each group to further streamline the multiplication process. By strategically choosing these pairs, the multiplier can achieve a lower error distance while maintaining acceptable accuracy levels. This strategy is crucial in approximate computing scenarios where slight errors in the result are permissible in exchange for significant gains in performance and power efficiency.

C. Simulation Outcome for Partial Product Generation

Simulations conducted on the generation of partial products using radix-256 Booth encoding with partial encoding strategy have demonstrated promising results. The method effectively reduces the number of partial products compared to conventional Booth encoding, leading to faster multiplication operations and reduced computational complexity. Moreover, the approximate summation unit associated with this approach ensures that the accumulated errors remain within acceptable bounds, making it suitable for various applications demanding high computational throughput.

D. Disadvantages

While radix-256 Booth encoding with partial encoding strategy offers significant advantages in terms of performance and power efficiency, it is not without its limitations and drawbacks it has increased complexity in encoding logic for implementing radix-256 encoding and the partial encoding strategy requires additional logic to manage the grouping and pairing of bits. This complexity can impact design verification, debugging, and overall development time.

Limited error distance to minimize error distance by carefully selecting bit pairs. However, inherently imposes limits on the maximum allowable error, which may not be suitable for applications requiring strict accuracy guarantees. It introduce overhead in terms of area utilization and timing constraints. While the multiplier may reduce overall resource usage, the additional logic required for encoding and error management could offset some of these gains. Compatibility Issues with all architectures or applications. It may require specific adaptations or optimizations depending on the target platform and design constraints. It can can be challenging due to the complexity of encoding logic and the potential for subtle errors in bit pairing and summation.

While radix-256 Booth encoding with partial encoding strategy represents a significant advancement in multiplier design, particularly for applications prioritizing performance and power efficiency, it is essential to carefully consider these disadvantages of specific design requirements and constraints.

IV. PROPOSED METHOD

A. Clock Gating

Reduction in power dissipation is an essential design issue in VLSI circuit. Few decades back designers mostly focus on area, delay and testability to optimize. While technology scaling down, we can see more power leakage and dissipation in chip. In order to reduce power dissipation and leakage power while scaling, we need to adopt the optimize techniques like clock gating, voltage scaling etc. If operations are more and more complex then power dissipation is more. The clock network is a major source of power dissipation so we can reduce significant amount of power if we can gate the clock whenever it isn’t required. In this work, we mainly focused on dynamic power dissipation and it reduced by making less signal activities in proposed design.

The clock network is a major source of power dissipation so we can reduce significant amount of power if we can gate the clock whenever it isn’t required.

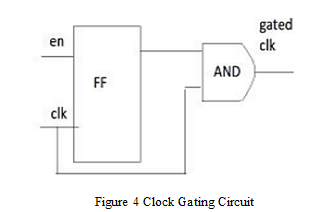
B. Flipflop-Based Clock Gating

Flip-flop clock gating is a technique used in digital circuit design to reduce power consumption by selectively disabling the clock signal to certain flip-flops when their state is not needed for computation or memory storage. This approach helps mitigate dynamic power dissipation, which is a significant concern in modern integrated circuits, especially in high-performance computing and low-power applications.

1) Operation of Flipflop based Clock Gating

The fundamental principle behind flip-flop clock gating involves controlling the clock input to individual flip-flops based on specific conditions. Typically, a gating logic circuit is employed to determine whether the clock signal should propagate to the flip-flop. When the gating condition is met (often based on the state of control signals or data dependencies), the clock signal is allowed to pass through to the flip-flop, enabling it to update its state. Conversely, when the gating condition is not satisfied, the clock signal is blocked or gated, preventing unnecessary state transitions and conserving power.

The implementation of flip-flop clock gating involves designing a gating logic circuit that evaluates the gating conditions and controls the clock signal accordingly. This circuit typically consists of combinational logic gates (such as AND, OR, and NOT gates) that process input signals to generate an enable signal for the clock. In many applications, latch-based designs are moved to flip flop based designs. By splitting flip flop, we can see two latches from the master slave theorem. In this technique, we can see D flip flop with AND gate.

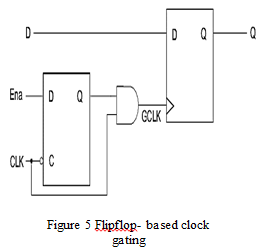
From the above figure, gated clock goes to high when flip flop output and clock are in high state otherwise gated clock goes to zero state. That means when clock in sleep mode then gated clock also in zero state.

V. RESULTS

A. RTL schematic

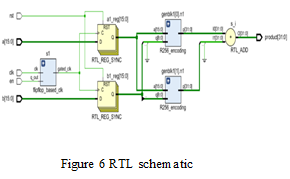
B. Technology Schematic

C. Simulation results

The parameters for the simulation results are clk, rst, en,inputs(a,b), product(gated_clk),temp

Here given clk=1, en=1

                     Clock period =10ns

                    Clock frequency= ~100MHz

                     inputs a=00cc, b=00ef [16-bit operands]

                     product=0000be74 [32-bit product]

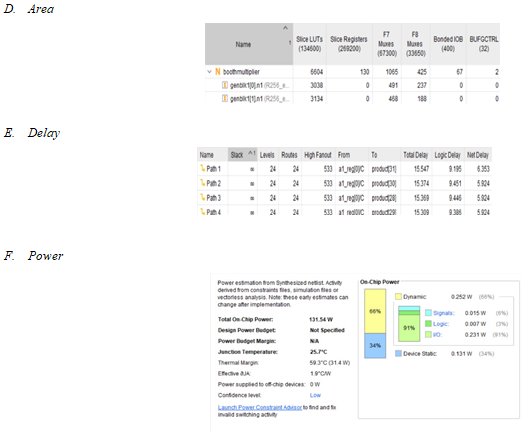
Comparison Table

Conclusion

This proposed approach excels in improving computational efficiency by using clock gating techniques, and enabling real-time processing capabilities. This approach reduces delay and power dissipation by disabling inactive clock signals. Its versatility allows seamless integration into existing systems. This method integrates well into telecommunications, audio processing, image and video processing, digital communication systems, medical signal processing, and many other domains. By truncating less significant bits, it maintains accuracy while lowering computational demands, resulting in substantial power savings. It offers a competitive advantage to organizations and industries that adopt this optimized approach, delivering faster and more efficient solutions to meet the demands of modern signal processing applications.

References

[1] Senthilkumar N, Bharanidharan K, Elanchandhar Pon, Akash kumar M, “Truncated Booth Multiplier Design Of Approximate Compressors Using Verilog Hdl” IEEE 9th International conference on Advanced computing and Communications Systems. [2] Feiyu Zhu, Shaowei Zhen, member, IEEE, Xilin Yi, Haoran Pei, Bowen Hou,and Yajuan He, Member, IEEE, “Design of Approximate Radix-256 Booth Encoding for Error-Tolerant Computing” IEEE Transactions On Circuits And Systems-II, April 2022. [3] Tingting Zhang , Graduate Student Member, IEEE, Honglan Jiang, Member, IEEE, Hai Mo, Weiqiang Liu , Senior Member, IEEE, Fabrizio Lombardi , Life Fellow, IEEE, Leibo Liu , Senior Member, IEEE, and Jie Han , Senior Member, IEEE “Design of Majority Logic-Based Approximate Booth Multipliers for Error-Tolerant Applications” 2022. [4] Patri Sanjana, Mehana Ramesh, Anushka Kale Vellore Institute of Technology Chennai, Anita Angeline A, Sasipriya P Centre for Nanoeletronics and VLSI design Vellore Institute of Technology Chennai, “Design and Evaluation of Error Tolerant Booth Multipliers for Image Processing Applications” 2022. [5] Marcello Traiola, Elena-Ioana Vatajelu and Angeliki Kritikakou, Electronics 2022, “Approximate Floating Point Multiplier based on Static Segmentation” 2022. [6] Y. Wu, et al. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, “Design and Performance Evaluation of Approximate Parallel Multipliers for High-Speed Signal Processing”. [7] M. Zhang and Q. Li , IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, “ Approximate Compressors in Booth Multipliers: A Comparative Study. [8] A. Kumar and R. K. Sharma IEEE Transactions on Circuits and Systems II: Express Briefs, 2021,“Efficient Design of Approximate Booth Multipliers for Error-Tolerant Applications” [9] N. Jain and V. Gupta, IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2021, “Design and Performance Evaluation of Truncated Booth Multiplier Using Adaptive Hybrid Adder Tree”.

Copyright

Copyright © 2024 K Pavithra Varsha, Dr. V. Sumalatha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.