Graphene: Study in Electronic Structure, Superconductivity and Potential in Quantum Information Sciences

Abstract

Graphene, a two-dimensional lattice of carbon atoms, exhibits remarkable electronic properties due to its Dirac-like electronic excitations. This paper reviews the elementary electronic properties of graphene, including the tight-binding model for single-layer graphene and the band structure formation. The tight-binding Hamiltonian provides a fundamental understanding of graphene’s linear energy dispersion near the Dirac points, leading to unique phenomena such as massless Dirac fermions and chiral tunneling. We explore the potential of superconductivity in graphene using BCS theory. We find that BCS theory cannot explain superconductivity in graphene and its forms. This is in contradiction with the discovery of unconventional superconductivity in twisted bilayer graphene (TBG). The study further explores the potential application of bilayer graphene quantum in quantum information sciences, highlighting the development of states with relaxation times exceeding 500 ms. These valley states, arising from the hexagonal lattice structure, can be used to encode information as robust valley qubits for fault-tolerant quantum computing.

Introduction

I. INTRODUCTION

Graphene, a two-dimensional lattice of carbon atoms arranged in a honeycomb structure, was first isolated in 2004 using mechanical exfoliation by Novoselov and Geim, who were later awarded the Nobel Prize for their work [1][2]. This groundbreaking discovery revealed that graphene exhibits unique electronic properties, such as massless Dirac fermions, high electron mobility, and the quantum Hall effect [3][4]. Graphene’s tunable electronic properties, including linear energy dispersion near the Dirac points, have sparked significant interest in its potential for superconductivity and quantum computing applications. In particular, twisted bilayer graphene (TBG), where two layers are twisted at a magic angle of approximately 1.1°, has been shown to exhibit unconventional superconductivity resembling that of high temperature cuprate superconductors [5].

In graphene, the valley degree of freedom refers to the electronic property arising from the presence of two inequivalent Dirac points (K and K’) in the first Brillouin zone, where electrons can occupy states in either valley, thus providing an additional quantum number that can be manipulated for information processing. Recent studies have demonstrated the potential of using valley states in bilayer graphene as robust qubits in quantum computing architectures. Recently, it was found that the relaxation times of valley states in gate-defined bilayer graphene quantum exceed 500 ms, significantly longer than spin relaxation times[6]. This remarkable stability positions valley qubits as promising candidates for fault-tolerant quantum computing. This paper reviews the elementary electronic properties of graphene, explores superconductivity in twisted bilayer graphene (TBG), and examines the potential application of bilayer graphene quantum dots in quantum information sciences

II. ELEMENTARY ELECTRONIC PROPERTIES OF GRAPHENE

A. Single Layer: Tight-Binding Approach

The tight binding approach is commonly derived for graphene to explain its electronic properties. Here is a derivation taken from Castro Neto et al. (2009), Legett (2010), and Utermohlen(2018) for the purpose of familiarizing readers with the basic terminologies of graphene. Graphene consists of carbon atoms arranged in a honeycomb lattice, which can be viewed as a triangular lattice with a two-atom basis per unit cell. Using Figure 1, we can calculate the lattice vectors as follows:

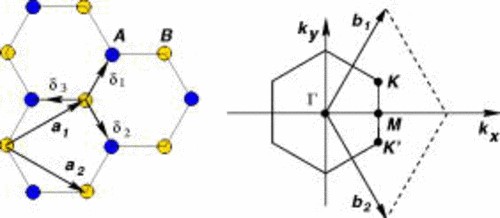
Figure 1: Honeycomb lattice structure of graphene (left) and its Brillouin zone (right). The Dirac cones are located at the K and K′ points. Figure from Castro Neto et al. (2009).

The primitive lattice vectors of graphene are:

                                              (1)                                                                 

where a = 1.42A? is the carbon-carbon distance.

The reciprocal lattice vectors are:

                                                                                                      (2)

In momentum space, the Dirac points at the corners of the Brillouin zone (BZ) are:

                                                  .                                                     (3)

The tight-binding Hamiltonian is a fundamental model for understanding the electronic band structure of solids, especially for materials like graphene with complex lattice structures. When considering only nearest-neighbor interactions, the tight-binding Hamiltonian for graphene is:

                                                                        ,                                                                  (4)

where:

• t: nearest-neighbor hopping parameter,
•  : creation (annihilation) operator for an electron at the A sublattice site at position ri,
• : creation (annihilation) operator for an electron at the B sublattice site at position rj,
• ⟨ij⟩: sum over nearest neighbors.

To express this Hamiltonian more explicitly, we rewrite the sum over nearest neighbors:

                                                  ,                                            (5)

where:

• i ∈ A: sum over A sublattice sites,
• δ: sum over the nearest-neighbor vectors δ1, δ2, and δ3,
• The operator ˆbi+δ annihilates a fermion at the B sublattice site at position ri + δ.

Using the Fourier transforms:

                                                                                                                                    (6)

                                     (7)

where N/2 denotes the number of A sublattice sites, we can rewrite the Hamiltonian in terms of momentum space operators.

Thus, the tight-binding Hamiltonian is:

                                                                                                      (8)

where:

                                                                           .                                                                      (9)

The Hamiltonian can now be expressed in matrix form as:

                                                                                                                            (10)

                                                                   ,                                                          (11)

and:

                                                                           ,                                                                   (12)

with:

                                                                                                                                                                   (13)

Hence, now the energy bands can be found by solving the eigenvalue problem for the Hamiltonian matrix h(k). The eigenvalues are:

                                                                                ,                                                                         (14)

which requires explicit calculation of ?k. Let’s compute it in terms of the nearest-neighbor vectors δi:

                                                                                       (15)

(15)

Thus, the energy bands are given by:

                        .                  (16)

Alternatively, they can also be expressed as:

                                                                                                              (17)

where:

                                         .                                (18)

Solving the equation for a dispersion plot yields interesting results.

III. BAND STRUCTURE OF GRAPHENE

We can use equation 18 obtained to plot the E-k relationship. This result was first obtained by Wallace in 1947 [9]. The E-k relationship can be better expressed in terms of the E-q relationship:

                                                                ,                                                         (19)

where:

• q = k − K is the momentum measured relative to the Dirac points in equation 18.
•  m/s is the Fermi velocity.

The relationship is plotted in figure 2. The conduction (upper) and valence (lower) bands meet at two special points in the Brillouin zone, known as Dirac points, forming gapless bands with linear dispersion. In conventional metals, electrons follow a parabolic energy-momentum relationship:

,

where m is the electron’s effective mass, leading to a velocity that varies with energy:

.

In contrast, graphene exhibits a linear energy-momentum relationship near the Dirac points:

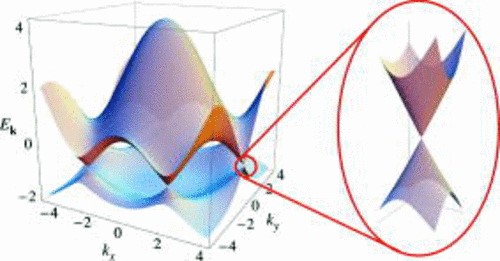
Figure 2: Electronic band structure of graphene showing the formation of linear dispersion at Dirac points. Adapted From Castro Neto et al. (2009) [7]

As a result, the Fermi velocity in graphene remains constant and independent of energy or momentum:

.

IV. DENSITY OF STATES IN GRAPHENE NEAR THE DIRAC POINTS

To derive the density of states (DOS) near the Dirac points in graphene, we start with the linear energy dispersion relation near the Dirac points:

                                                                                                                                                                   (20)

The magnitude of the wavevector |k| in terms of energy E is:

                                                                                         .                                                                                 (21)

The number of electronic states within a wavevector circle of radius k is:

                                                                                                                                                           (22)

where g = 4 is the degeneracy factor (2 from spin, 2 from valley), and Ak = πk2 is the area of the circle. Thus, the the number of states are:

                                                                                                                                                 (23)

Expressing k in terms of energy:

                                                                                                                                                                             (24)

so,

                                                                                                                                 (25)

The density of states (DOS) is given by the derivative of the number of states with respect to energy:

                                                                                                                                    (26)

Incorporating the unit cell area Ac:

                                                                                                                                                                     (27)

Thus, the density of states per unit cell is:

                                                                                                                  (28)

V. TESTING SUPERCONDUCTIVITY IN GRAPHENE AND BILAYER GRAPHENE USING THE BCS EQUATION

The fundamental BCS equation relates the critical temperature (Tc) to the Debye energy (hω¯ D) and the dimensionless coupling constant (λ):

                                                                     .                                                             (29)

where kB is the Boltzmann constant,  is the Debye energy, λ = N(EF )V is the dimensionless coupling constant, N(EF ) is the density of states at the Fermi level, V is the effective pairing potential.

In undoped pure graphene, the density of states (DOS) near the Dirac point (E = 0) is given by:

,

Therefore, the density of states at the Fermi level for grapheme

0. Plugging the value into the coupling constant, we get zero. Hence, Finally, plugging the value of the coupling constant in equation 29, we get the value of critical temperature to be zero. This indicates the absence of superconductivity in graphene. The key point to realize is that the small density of states (DOS) close to the Dirac point results in a lack of superconductivity in graphene.

This result is not too different for bilayer graphene, which essentially has a similar trend in the E-q relationship.

VI. UNCONVENTIONAL SUPERCONDUCTIVITY IN TWISTED BILAYER GRAPHENE (TBG)

Even though, graphene itself is not superconducting, superconductivity was discovered in twisted bilayer graphene (TBG)in 2018 when Cao et al. observed that graphene sheets twisted at a “magic angle” of approximately 1.1° exhibited unconventional superconductivity at a critical temperature (Tc) of around 1.7 K [5]. In the phase diagram of TBG, the superconducting region forms a “dome” when plotting critical temperature as a function of carrier density or twist angle. This means that superconductivity appears within a certain range of these parameters and vanishes outside of it, similar to what is seen in high-Tc cuprate superconductors. In both systems, there is a critical region where superconductivity is maximized, flanked by other electronic phases such as the correlated insulating state found at half-filling of the flat band in TBG. This discovery demonstrated that TBG could be tuned to host strong electron-electron correlations and unconventional superconductivity by varying the carrier density and the twist angle.[9].

Superconductivity in TBG arises due to the formation of flat electronic bands at the magic angle, which enhances the density of states and electron-electron interactions [9]. The flat-band superconducting state is described by a mean-field theory equation, where the superconducting gap ? is approximated by:

                                                                                    ,                                                                            (30)

where λ represents the electron-phonon coupling strength and ?FB is the area of the first Brillouin zone [10].

Furthermore, the density of states (DOS) near the magic angle in TBG potentially displays a distinctive spiking feature, a hallmark of the flat band condition at this angle [10]. This flat band leads to a dramatic enhancement of the DOS, which in turn facilitates strong electron-electron interactions and promotes the emergence of correlated insulating states and superconductivity. The spiking feature in the DOS is a consequence of the nearly dispersionless bands, which arise due to the unique moire superlattice formed at the magic angle.´

We can provide an argument as to the cause of superconductivity such that the electron phonon coupling (λ) potentially mediates an effective attractive interaction between electrons via virtual phonon exchange, potentially overcoming the Coulomb repulsion at low temperatures and facilitating the formation of Cooper pairs. This mechanism, central to conventional

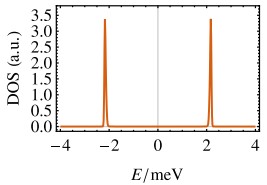
Figure 4: Density of states in TBG in the superconducting state. From Peltonen et al. [10]

Superconductors, can be generalized to account for anisotropic pairing interactions, potentially giving rise to unconventional superconducting states of different symmetries. Additionally, strong Coulomb interactions can potentially enhance these anisotropic interactions by promoting electronic correlations that favor non-trivial pairing symmetries, thereby potentially enabling pairing mechanisms that deviate from the isotropic s-wave symmetry, potentially leading to exotic superconducting phases with higher critical temperatures or novel physical properties.

The unique electronic properties of magic-angle TBG, characterized by its tunable flat bands and strong correlations, provide an opportunity to explore the mechanisms behind unconventional superconductivity. This system can serve as a ground for examining the role of electron correlations, band topology, and symmetry in the emergence of superconducting and insulating phases. As such, magic-angle TBG stands out as a prime candidate for advancing our understanding of strongly correlated electron systems and the complex interplay between superconductivity and other emergent quantum phases.

VII. POTENTIAL APPLICATION IN QUANTUM INFORMATION SCIENCES

An interesting question is if graphene and its multilayer forms can be explored for making qubits. One particular study by Garreis et al. (2024) explores using valley states in bilayer graphene as qubits[6].

The bilayer form of graphene provides additional degrees of freedom, such as the valley degree of freedom, which arises from its hexagonal lattice structure. Electrons in bilayer graphene occupy one of two valleys (K and K’), providing an additional quantum number akin to spin. These valley states can be used to encode information and their distinct locations in reciprocal space result in valley qubits that are robust against spin and orbital mixing mechanisms. According to the author, the electrically tunable valley g-factor can allow precise manipulation of these states, making them promising candidates for qubits in quantum computing. A potential advantage in this system is that of the Pauli Valley blockade effect which occurs when electron transport is hindered due to the electrons’ valley degree of freedom. It can be taken as an additional quantum number representing different energy minima in the band structure. This effect allows for precise readout of electronic states by selectively blocking certain transport paths, thereby enhancing measurement accuracy. Consequently, this high-fidelity state readout supports the potential use of these systems in developing robust, fault-tolerant quantum computing architectures.

In the study, relaxation times of valley states in gate-defined bilayer graphene quantum structures were measured and found to exceed 500 ms, more than one order of magnitude longer than the relaxation times of spin states [6]. This remarkable longevity makes valley qubits in bilayer graphene exceptionally stable. The characteristic relaxation times T1 were obtained using pulsed gate voltages and analyzed with a Bayesian exponential model. The spin relaxation time was up to 60 ms at B⊥ = 700mT, while the valley relaxation time exceeded 500 ms at B⊥ = 250mT. These findings highlight the potential of bilayer graphene as a platform for long-lived and electrically controllable qubits.

Conclusion

Graphene, with its unique electronic properties such as massless Dirac fermions and high electron mobility, has revolutionized the field of condensed matter physics. Although BCS theory cannot explain superconductivity in graphene due to the small density of states at the Dirac point, the discovery of unconventional superconductivity in twisted bilayer graphene (TBG) has opened new avenues for research. The formation of flat electronic bands at the magic angle in TBG enhances electron-electron interactions, leading to correlated insulating states and unconventional superconductivity. Furthermore, the valley degree of freedom in bilayer graphene quantum dots provides a robust platform for quantum information sciences, with valley states offering relaxation times exceeding 500 ms, making them promising candidates for fault-tolerant quantum computing. Understanding these properties and phenomena lays the groundwork for advances in graphene-based superconductivity and quantum computing architectures.

References

[1] K. S. Novoselov et al., \"Electric field effect in atomically thin carbon films,\" Science, vol. 306, pp. 666–669, 2004. [2] K. S. Novoselov and A. K. Geim, \"Nobel Lecture: Graphene: Materials in the Flatland,\" Rev. Mod. Phys., vol. 83, pp. 837, 2011. [3] K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and A. A. Firsov, \"Two-dimensional gas of massless Dirac fermions in graphene,\" Nature, vol. 438, no. 7065, pp. 197–200, Nov. 2005. [4] M. Katsnelson, K. Novoselov, and A. Geim, \"Chiral tunnelling and the Klein paradox in graphene,\" Nature Phys., vol. 2, pp. 620–625, 2006. [5] Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, \"Unconventional superconductivity in magic-angle graphene superlattices,\" Nature, vol. 556, no. 7699, pp. 43–50, 2018. [6] R. Garreis, C. Tong, J. Terle, et al., \"Long-lived valley states in bilayer graphene quantum dots,\" Nat. Phys., vol. 20, pp. 428–434, 2024. [7] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, \"The electronic properties of graphene,\" Rev. Mod. Phys., vol. 81, 2009. [Online]. Available: https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.81.109 [8] A. J. Leggett, \"Lecture 5: Graphene: Electronic band structure and Dirac fermions,\" 2010. [Online]. Available: http://web.physics.ucsb.edu/phys123B/w2015/leggett-lecture.pdf [9] P. R. Wallace, \"The band theory of graphite,\" Phys. Rev., vol. 71, p. 622, 1947. [10] T. J. Peltonen, R. Ojajarvi, and T. T. Heikkila, \"Mean-field theory for superconductivity in twisted bilayer graphene,\" arXiv preprint, arXiv:1805.01039, 2018. [11] Utermohlen, \"Graphene Tight-Binding Model,\" Department of Physics, The Ohio State University, 2018. [Online]. Available: https://cpb-us-w2.wpmucdn.com/u.osu.edu/dist/3/67057/files/2018/09/graphene_tight-binding_model-1ny95f1.pdf

Copyright

Copyright © 2024 Aditya Chapagain. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.