A Review of Empirical Methods for Runoff Estimation and Their GIS Applications

Abstract

Irregularities in rainfall patterns, frequent floods, and droughts in different parts of the world result from the effects of global climate change. In such dynamic climatic conditions, sustainable management of water resources is a challenging task under a river basin\'s complex process response system. In this perspective, hydrological studies are being carried out to estimate the runoff water yield and understand physico-climatic controls require further development in methodologies. Research criteria have advanced and empirical method\'s development and applications have advanced significantly. Empirical methods quantify the runoff volume by correlating the amount of rainfall with the number of influencing basin factors. In recent times, empirical runoff estimation has become popular because of its simplicity and correlation assessment capacity with multiple associate factors. This study aims to have an overview of the empirical runoff estimator SCS-CN method and other empirical equations. This study has covered the primary areas in hydrological analysis are runoff estimation, groundwater recharge, and runoff-soil erosion estimation using empirical methods. The authors have suggested the advantages, disadvantages, and possible areas of development of the widely used SCS-CN method and other empirical methods of runoff estimation.

Introduction

I. INTRODUCTION

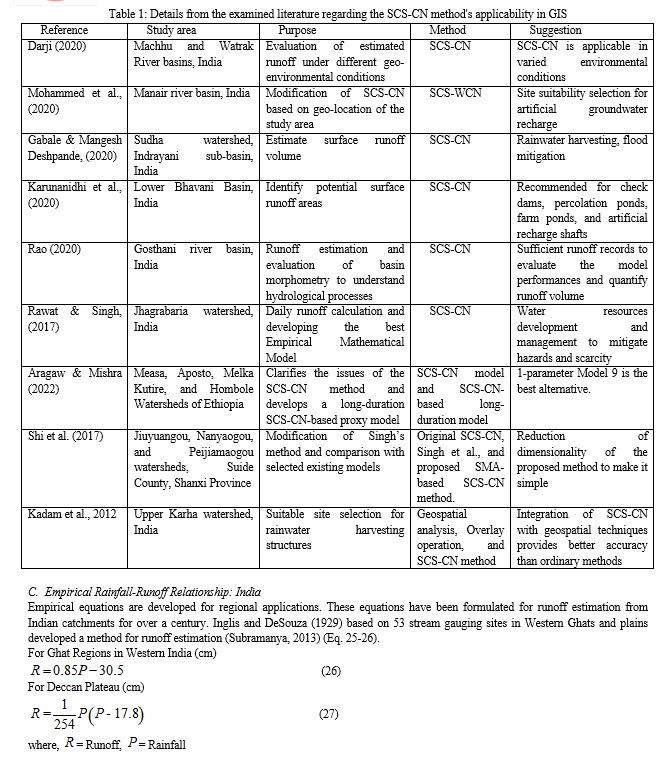
The overland flow of excess rainfall is called surface runoff and initially joins a stream network in a basin system. Through a series of channel networks, the runoff water eventually enters the master stream. The volume of water measured at the basin outlet is known as stream flow or total runoff, and it consists of base flow, interflow, and overland flow (Betson, 1964). The total volume of surface runoff is influenced by several factors, such as the rate of infiltration, soil properties, rainfall intensity, vegetation cover, basin morphometry, and meteorological conditions (Kothyari & Garde, 1991). A major component of hydrological modelling is the total runoff or streamflow. Therefore, measurement of runoff is a crucial part of any hydrological modelling (S. Verma et al., 2017). In recent decades, the SCS-CN method has been widely applied in different parts of the world to estimate runoff depth and volume (Abdi & Meddi, 2021; Rajasekhar et al., 2020). SCS-CN method was developed by the United States Department of Agriculture (1956) and is a widely used simple, reliable, and attractive method for estimating runoff from given rainfall (Sangin et al., 2023). This approach necessitates the use of easily available tables and curves as well as a simple empirical formula. SCS-CN method uses minimal numbers of input parameters. Here, CN denotes the runoff potentials that are measured using LULC, different types of antecedent moisture conditions, and soil types (Kadam et al., 2012; Rawat & Singh, 2017).

The framework of this review study is categorized under two broad classes (Fig. 1) as Model-based runoff estimation and application: SCS-CN, and Runoff Estimation and application using equations.

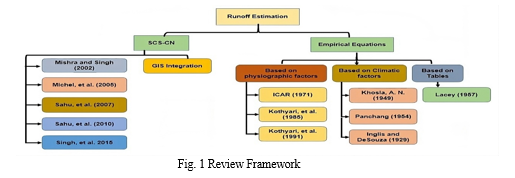
Using GIS and remote sensing thematic data layers are generated. Integration of GIS and RS with SCS-CN very accurately estimates the depth and volume of runoff as reported in different studies (Kumar et al., 2021; Saha et al., 2022; Satheeshkumar et al., 2017). Saha et al. (2022) used annual rainfall data for their study. They reported the correlation between rainfall-runoff is 0.98. As they mentioned, the average runoff depth that occurred annually during the study period was 979.45 mm in response to 1341.59 mm of rainfall. The depth of runoff is quite high and 73% of the average annual rainfall. Satheeskumar et al. (2017) used 14 years of rainfall data to estimate the annual runoff depth and volume. They presented that the correlation between rainfall and runoff is 0.84, which means the relation is highly correlated. They measured the average annual volume and depth of runoff are 32682501 m2 and 181.731 mm where the rainfall was 848.56 mm. The drainage basin of this study drains only 21% of water.

Jiao et al. (2015), in their study, modified the SCS-CN method and used it for runoff prediction for different land practices. They have compared the performance between the original and improved methods and noticed the prediction accuracy varies for each land practice. Their improved SCS-CN method predicted better accuracy than the original one. Singhai et al. (2019) estimated the surface runoff for the period 1997 to 2006. Their estimated value is under-predicted compared to the actual value for each year. The drainage basin yields 42% water from the average rainfall and is available for utilization and management. Kadam et al. (2012) also conducted a similar study to predict the runoff for different land classes using the Arc-CN Runoff tool. To estimate the runoff depth geospatial technology has been used for different watersheds across India (Rawat and Singh, 2017; Rao, 2020; Karunanidhi et al. (2020); Gabale and Deshpande, 2020; Mohammed et al., 2020). They adopted the original SCS-CN method for their study and reported that the SCS-CN method had the best performance for runoff estimation in different physical settings.

B. Suitable Site Selection for Rainwater Harvesting: Application of GIS-based SCS-CN

The construction of rainwater harvesting structures is a management strategy in order to remediate the vulnerabilities of groundwater resources. Percolation tanks, Farm ponds, check dams, and gully plugs are the important rainwater harvesting structures mentioned in different studies worldwide. Kadam et al. (2012) using GIS and remote with SCS-CN method have identified suitable sites for structuring rainwater harvest. They utilized overlay operation in the GIS environment for this purpose and secured 86. 25% average accuracy. The multi-criteria Decision-Making approach was used by Singhai et al. (2017) to define suitable sites for check dams, farm ponds, and percolation tanks. They presented 70-100% overall accuracy in the validation phase. Rajasekhara, M.et al. (2020) adopted the AHP method in order to determine the sites for recharging groundwater. In this study, they considered check dams, farm ponds, and percolation tanks as recharge mediator. They have identified a total of 35 potential sites for harvesting rainwater with 82% accuracy. Multi-influencing factor (MIF) is a geospatial technique used for considering the effects of parameters and their interaction. Pandey et al. (2021) determined the potential recharge zones using the MIF method. For this purpose, they used LULC, soil, slope, drainage density, geomorphology, and depth of water level as influencing factors.

???????C. Flood Potentiality Estimation: Application of GIS-based SCS-CN

Recently, many researchers have explored the ability of the SCS-CN method along with the GIS interface in the flood potentiality estimation process. Sharma and Singh (2014) used the SCS-CN method to estimate the flood potentialities for different sub-basins within the main study area using parameters like DEM, rainfall, LULC, and soil data. At first, they estimated the runoff potentialities for each sub-watershed, correlated that with gauge data, and found higher accuracy.  Abdi and Meddi (2020) emphasized the use of GIS integrated SCS-CN method to determine the flood potentialities in an ungauged river basin. Four models such as Mishra et al. (2006), Sahu et al. (2010), Singh et al. (2015), and Verma et al. (2017) are compared with the original SCS-CN method. They presented the predominance of the modified models over the original SCS-CN model and suggested applying these models in different watersheds for validation purposes.

III. RUNOFF ESTIMATION AND APPLICATION USING EQUATIONS

A. Runoff estimation using Empirical equations

Inglis and DeSouza (1929) developed an equation to estimate annual runoff for the catchments in the Western Ghats and Plains of Western India. They used annual rainfall and coefficients for runoff estimation. The Western Ghats is made up of hard rocks, and a higher runoff amount is expected than the plains. Inconsistency is noticed between the formulas because the equation developed for plains calculates a higher runoff value. Khosla (1949), formulated a runoff estimation equation by addressing the loss factor. He used annual rainfall data, and temperature data to formulate the equation and found it to yield good estimates of annual runoff. Panchang (1954) modified the equation proposed by Khosla (1949). Evaporation increases with the increase in temperature. He introduced the evaporation factor in his method as a loss factor.

Raja Rao and Pentaih (1971) used data from four Andhra Pradesh catchments to investigate the efficacy of Khosla's original and modified equations. They concluded that neither the modified Panchang model nor the estimations from Khosla's original calculation agreed with the runoff values that were observed (Ramasastri and Seth, 1985).

Kothyari et al. (1985) derived a new method for runoff estimation. In this method, he introduced the vegetation factor as a runoff-controlling factor. He used 26 basins to derive the formula. Kothyari et al. (1991) found inconsistencies in their previous method and developed another equation using 55 catchment data across India. They presented the better performance of the modified method compared to the previous method.

???????B. Soil erosion estimation from runoff

In recent years, soil erosion estimation by using the RUSLE model has been a popular and widely accepted method among researchers. The main parameter of the model is the runoff erosivity (RE) factor. RE factor required an equation to generate the model. There is no single equation that can be utilized across the world. This equation varies significantly among the researchers and from region to region. So, the researchers used regionally developed empirical equations to develop the model. Arnoldus (1980) developed an equation for runoff estimation. It has been noticed that researchers across the world frequently used the equation developed by Arnoldus (1980). It is not possible to address the effectiveness of this method for different watersheds. Because empirical equations are directly applied in models without checking the validity of the equations.

IV. MAJOR FINDINGS

1. Despite several modifications, the SCS-CN method has received a lot of popularity because of its straightforward conceptual approach for runoff prediction in ungauged river basins worldwide. 
2. Modifications underpinned the original SCS-CN method in order to achieve region-specific higher efficiency.
3. Integration of SCS-CN with GIS has strengthened the prediction results with an accuracy of more than 80%. The applications of hybrid methods expanded the scope of the study.
4. Considering the basin complexities empirical runoff estimation equations are developed over time to overcome the prediction errors.
5. Empirical runoff estimation equations consider the regional morphometric and climatic parameters that demonstrate improved prediction accuracy.
6. The RUSLE model is simple and suitable for soil erosion predictions. Here, the use of empirical equations exemplifies the desired accuracy because of its regional properties.

Conclusion

Runoff estimation is essential for hydrological modelling, sustainable water resources management, and planning. Runoff is a dynamic process, generated through the complex process-response system of a drainage basin. To estimate the runoff depth for any catchment, there is a need for a method that can correlate the complexities of the basin. In recent times, most of the drainage basins have no proper gauge stations that can monitor the stream runoff depth and other basin parameters across the world. This study attempted to analyze the applications of SCS-CN and empirical equations for runoff estimation based on existing contributions. SCS-CN method presented an outstanding performance with more than 80% accuracy across the globe. Similarly, empirical equations performed well in all formats of runoff estimation. Several scholars utilized empirical equations for runoff and soil erosion estimation. It has been reviewed from the previous studies that all of the methods analyzed in this study performed well with maximum accuracy. This study evaluated the applications of SCS-CN and empirical equations on runoff estimation and allied applications under different physico-climatic conditions. Another purpose of this study was to consider the conventional methods used in different environmental settings for runoff estimation, to uncover the most suitable alternatives for runoff estimation under varied natural processes. Additionally, this review process found that the modified methods under a specific natural system presented higher accuracy than the original methods. Another important outcome of this study is the application of runoff estimation methods along with GIS opened multiple dimensions for hybrid study. This study recommends that researchers use the updated SCS-CN method and empirical equations for their study. This study demonstrates problems related to runoff estimation when considering moisture conditions and other factors. To resolve this issue, future researchers can develop a framework integrating GIS and runoff estimation methods to achieve better model performances. Future researchers can use hybrid models that consider the wide range of physico-climatic controls for estimating runoff depth and allied applications.

References

[1] Abdi, I., & Meddi, M. (2021). Study on the applicability of the SCS-CN-based models to simulate floods in the semi-arid watersheds of northern Algeria. Acta Geophysica, 69(1), 217–230. https://doi.org/10.1007/s11600-020-00511-3 [2] Aragaw, H. M., & Mishra, S. K. (2022). Clarification of issues and long-duration hydrologic simulation SCS-CN-based proxy modelling. Acta Geophysica, 70(2), 729–756. https://doi.org/10.1007/s11600-022-00730-w [3] Belayneh, M., Yirgu, T., & Tsegaye, D. (2019). Potential soil erosion estimation and area prioritization for better conservation planning in Gumara watershed using RUSLE and GIS techniques’. Environmental Systems Research, 8(1). https://doi.org/10.1186/s40068-019-0149-x [4] Betson, R. P. (1964). What Is Watershed Runoff? Journal of Geophysical Research, 69(8). https://doi.org/10.1029/JZ069i008p01541 [5] Chakrabortty, R., Pradhan, B., Mondal, P., & Pal, S. C. (2020). The use of RUSLE and GCMs to predict potential soil erosion associated with climate change in a monsoon-dominated region of eastern India. Arabian Journal of Geosciences, 13(20). https://doi.org/10.1007/s12517-020-06033-y [6] Darji, K. (2020). Runoff Estimation of Machhu and Watrak Rivers Basins of Gujarat India using SCS-CN Method and GIS. In Article in Indian Journal of Ecology. https://www.researchgate.net/publication/344463599 [7] Djoukbala, O., Mazour, M., Hasbaia, M., & Benselama, O. (2018). Estimating of water erosion in semiarid regions using RUSLE equation under GIS environment: Case of Wadi El-Ham watershed in Hodna region, Algeria. Environmental Earth Sciences, 77(9). https://doi.org/10.1007/s12665-018-7532-1 [8] Gabale, S., & Mangesh Deshpande, A. (2020). Geospatial technique for runoff estimation based on SCS-CN method in Sudha river basin of Indrayani River. International Journal of Multidisciplinary Research and Development www.Allsubjectjournal.Com, 7, 172–177. www.allsubjectjournal.com [9] Geol, N. K., & Chander, S. (2002). Regionalization of Hydrological Parameters. National Institute of Hydrology. Roorkee. [10] Ghosal, K., & Das Bhattacharya, S. (2020). A Review of RUSLE Model. In Journal of the Indian Society of Remote Sensing (Vol. 48, Issue 4, pp. 689–707). Springer. https://doi.org/10.1007/s12524-019-01097-0 [11] Kadam, A. K., Kale, S. S., Pande, N. N., Pawar, N. J., & Sankhua, R. N. (2012). Identifying Potential Rainwater Harvesting Sites of a Semi-arid, Basaltic Region of Western India, Using SCS-CN Method. Water Resources Management, 26(9), 2537–2554. https://doi.org/10.1007/s11269-012-0031-3 [12] Karunanidhi, D., Anand, B., Subramani, T., & Srinivasamoorthy, K. (2020). Rainfall-surface runoff estimation for the Lower Bhavani basin in south India using SCS-CN model and geospatial techniques. Environmental Earth Sciences, 79(13). https://doi.org/10.1007/s12665-020-09079-z [13] Kothyari, U. C., & Garde, R. J. (1991). ANNUAL RUNOFF ESTIMATION FOR CATCHMENTS IN INDIA. Journal of Water Resources Planning and Management, 117( 1). https://doi.org/10.1061/(ASCE)0733-9496(1991)117:1(1) [14] Kumar, A., Kanga, S., Taloor, A. K., Singh, S. K., & ?urin, B. (2021). Surface runoff estimation of Sind river basin using integrated SCS-CN and GIS techniques. HydroResearch, 4, 61–74. https://doi.org/10.1016/j.hydres.2021.08.001 [15] Michel, C., Andréassian, V., & Perrin, C. (2005). Soil Conservation Service Curve Number method: How to mend a wrong soil moisture accounting procedure? Water Resources Research, 41(2), 1–6. https://doi.org/10.1029/2004WR003191 [16] Moid Mohammed, A., Lakshmi Thatiparthi, V., Rao Pyla, K., & Maryada, A. (2020). Estimation of Surface Runoff in an Ungauged Basin Using SCS-CN Method, A Case Study of Manair River Basin in Telangana, India. Applied Ecology and Environmental Sciences, 8(6), 340–350. https://doi.org/10.12691/aees-8-6-3 [17] Nageswara Rao, K. (2020). Analysis of surface runoff potential in ungauged basin using basin parameters and SCS-CN method. Applied Water Science, 10(1). https://doi.org/10.1007/s13201-019-1129-z [18] Pandey, P., Tiwari, S. K., Pandey, H. K., Chaurasia, A. K., & Singh, S. (2021). Identification of Potential Recharge Zones in Drought Prone Area of Bundelkhand Region, India, Using SCS-CN and MIF Technique Under GIS-frame work. Water Conservation Science and Engineering, 6(3), 105–125. https://doi.org/10.1007/s41101-021-00105-0 [19] Pandi, D., Kothandaraman, S., & Kuppusamy, M. (2020). Delineation of potential groundwater zones based on multicriteria decision making technique. Journal of Groundwater Science and Engineering, Vol.8, 55–69. [20] Prasannakumar, V., Shiny, R., Geetha, N., & Vijith, H. (2011). Spatial prediction of soil erosion risk by remote sensing, GIS and RUSLE approach: A case study of Siruvani river watershed in Attapady valley, Kerala, India. Environmental Earth Sciences, 64(4), 965–972. https://doi.org/10.1007/s12665-011-0913-3 [21] Rajasekhar, M., Gadhiraju, S. R., Kadam, A., & Bhagat, V. (2020). Identification of groundwater recharge-based potential rainwater harvesting sites for sustainable development of a semiarid region of southern India using geospatial, AHP, and SCS-CN approach. Arabian Journal of Geosciences, 13(2). https://doi.org/10.1007/s12517-019-4996-6 [22] Ramasastri, K. S., & Seth, S. M. (1985). Rainfall-Runoff Relationships. National Institute of Hydrology, Roorkee, India. [23] Rawat, K. S., & Singh, S. K. (2017). Estimation of Surface Runoff from Semi-arid Ungauged Agricultural Watershed Using SCS-CN Method and Earth Observation Data Sets. Water Conservation Science and Engineering, 1(4), 233–247. https://doi.org/10.1007/s41101-017-0016-4 [24] Saha, A., Ghosh, M., & Pal, S. C. (2022). Estimation of rainfall–runoff using SCS-CN method and GIS techniques in drought-prone area of Upper Kangsabati Watershed, India. Sustainable Water Resources Management, 8(5). https://doi.org/10.1007/s40899-022-00731-z [25] Sahu, R. K., Mishra, S. K., & Eldho, T. I. (2010). Comparative evaluation of SCS-CN-inspired models in applications to classified datasets. Agricultural Water Management, 97(5), 749–756. https://doi.org/10.1016/j.agwat.2010.01.005 [26] Sahu, R. K., Mishra, S. K., & Eldho, T. I. (2012). Performance evaluation of modified versions of scs curve number method for two watersheds of maharashtra, India. ISH Journal of Hydraulic Engineering, 18(1), 27–36. https://doi.org/10.1080/09715010.2012.662425 [27] Satheeshkumar, S., Venkateswaran, S., & Kannan, R. (2017). Rainfall–runoff estimation using SCS–CN and GIS approach in the Pappiredipatti watershed of the Vaniyar sub basin, South India. Modeling Earth Systems and Environment, 3(1). https://doi.org/10.1007/s40808-017-0301-4 [28] Shi, W., Huang, M., Gongadze, K., & Wu, L. (2017). A Modified SCS-CN Method Incorporating Storm Duration and Antecedent Soil Moisture Estimation for Runoff Prediction. Water Resources Management, 31(5), 1713–1727. https://doi.org/10.1007/s11269-017-1610-0 [29] Singh, M. C., Sur, K., Al-Ansari, N., Arya, P. K., Verma, V. K., & Malik, A. (2023). GIS integrated RUSLE model-based soil loss estimation and watershed prioritization for land and water conservation aspects. Frontiers in Environmental Science, 11. https://doi.org/10.3389/fenvs.2023.1136243 [30] Singhai, A., Das, S., Kadam, A. K., Shukla, J. P., Bundela, D. S., & Kalashetty, M. (2019). GIS-based multi-criteria approach for identification of rainwater harvesting zones in upper Betwa sub-basin of Madhya Pradesh, India. Environment, Development and Sustainability, 21(2), 777–797. https://doi.org/10.1007/s10668-017-0060-4 [31] Subramanya, K. (2013). ENGINEERING HYDROLOGY Fourth Edition (4th ed.). McGraw Hill Education (India) Private Limited. New Delhi. India [32] Verma, R. K., Verma, S., Mishra, S. K., & Pandey, A. (2021). SCS-CN-Based Improved Models for Direct Surface Runoff Estimation from Large Rainfall Events. Water Resources Management, 35(7), 2149–2175. https://doi.org/10.1007/s11269-021-02831-5 [33] Verma, S., Mishra, S. K., Singh, A., Singh, P. K., & Verma, R. K. (2017). An enhanced SMA based SCS-CN inspired model for watershed runoff prediction. Environmental Earth Sciences, 76(21). https://doi.org/10.1007/s12665-017-7062-2

Copyright

Copyright © 2024 Sribas Kanji, Subhasish Das. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.