Enhancing Techniques for Adaptable Decision Feedback Balancer for 5G Communication

Abstract

This complete review examines two basic parts of cutting edge correspondence frameworks. First and foremost, it investigates novel plan procedures and models for Adaptable Decision Feedback Balancer (ADFB) in rapid correspondence frameworks. Strategies like look-into tables, disseminated math, and prescient equal branch slicers are utilized to upgrade union rates, throughput, and mistake execution while limiting equipment intricacy. The proposed plans exhibit significant advancement in region, power proficiency, and rationale usage across different regulation plans, channel models, and portability situations. Furthermore, the examination digs into Super Dependable Low Idleness Correspondence (SDLIC) headways inside the 5G New Radio (NR) downlink, tending to actual layer difficulties determined in 3GPP Delivery 15. The review presents a clever correspondence framework utilizing super codes to moderate between image impedance in remote conditions. Also, inventive equal plans for high velocity Choice Input Adjusters (CIAs) and equipment proficient models for versatile balancers utilizing disseminated number-crunching are introduced. The joined discoveries contribute significant bits of knowledge into streamlining versatile balancers for group of people yet to come correspondence frameworks and progressing SDLIC in 5G NR.

Introduction

I. INTRODUCTION

In the powerful scene of correspondence advances, different versatile leveling methods assume a critical part in guaranteeing proficient information transmission over assorted channels. This study paper dives into a thorough investigation of late progressions and novel philosophies in ADFBs. These are pivotal parts in alleviating issues like between image obstruction and improving the general execution of correspondence frameworks.

The overviewed papers include a range of points, going from creative plan procedures for ADFBs. to their application in various balance plans. Through fastidious examinations, specialists have proposed techniques to help intermingling rates, limit equipment intricacy, and streamline key execution measurements like throughput, mistake rates, and power utilization.

In this outline, we explore through the assorted commitments of these papers, tending to the complexities of versatile adjusters, novel models, and the effect of balance plans on their presentation. The undertaking reaches out to the complexities of versatile choice criticism balancers in wired and remote correspondence channels, stressing their job in battling contortion and further developing framework productivity.

Besides, the review researches novel methodologies, for example, pipelined choice supported balance, broadened gradual coefficients-look forward channels, and the combination of choice input RNN adjusters. These methodologies vow to upgrade the versatility, throughput, and power effectiveness of ADFBs.

As we advance, consideration is additionally given to the difficulties and creative arrangements in executing ADFBs, including equipment productive plans, calculation techniques, and ongoing contemplations. The overview embodies studies including equipment proficient reconfigurable FIR channel plans, versatile channels executed with dispersed math, and equal methodologies for fast choice input adjusters.

Moreover, the paper investigates methods like look-ahead approaches, prescient equal branch slicers, and inadequate fluffy displaying for hearty choice criticism evening out. The consideration of concentrates on distribution of asset in 5G frameworks and the advancing scene of SDLIC further enhance the comprehension of versatile adjustment in current correspondence situations.

II. LITERATURE SURVEY

The parameters for optimizing Adaptable Decision Feedback Balancer (ADFB) involves enhancing throughput, convergence rate, error performance, hardware efficiency and energy efficiency.

A. Harware Efficiency

Distributed Arithmetic can be used to implement FIR filters instead of Multiplier- Accumulator units to reduce the hardware complexity. Offset Binary Coding (OBC) technique can be used to reduce the LUT (Look Up Table) size to half.

In [3], an architectural design is presented for an ADFB with minimal complexity. This is realized by reformulating the ADFB equations using distributed arithmetic (DA), thereby eliminating the need for multipliers.

The architecture in [4] uses DA to implement ADFB. It is hardware efficient because it requires fewer adders and no multiplier units. For example, the suggested architecture utilizes about 20% low chip area and the power than the newly found architecture in the literature for an ADFB with a length of FBF to be 8. Also, it uses OBC scheme.

A novel hardware adaptive filter design for high-efficiency LMS adaptive filters is covered in this study [5]. This paper outlines the evolution of DA adaptive filters and demonstrates the extremely high throughput of real-world DA adaptive filter implementations as compared to multiply and accumulates architectures. It is shown that there may be an area and power consumption benefit to using DA adaptive filters over DSP microprocessor designs.

Two new DA-based implementation strategies for adaptive FIR filters are put forth in this brief. In contrast to traditional DA methods, the suggested systems access a set of LUTs storing sums of scaled and delayed input sample by using coefficients as addresses. In order to weights update and reduce the MSE among the desired and predicted output, two clever LUT updating techniques are designed and then LMS adaptation is carried out. These two high-performance designs achieve low computing complexity, low area cost, and high speed, according to the results [6].

The LUTs need to be adjusted because updating the filter coefficients is necessary when using an adaptive filter. To update these LUTs periodically, a novel approach [7] relying on the OBC method has been put forth. Based on simulation outcomes, for large base unit size k (where k=N/m, m is an integer, and N represents the number of filter coefficients), the proposed method delivers significant throughput gains while requiring relatively minimal chip area.

The work [8] presents a thorough examination of the design of a 16-tap FIR filter in VHDL using DA and “Off-Set Binary Coding” (OBC)-DA. Xilinx ISE is used for Virtex-4 ML 402 synthesis. Synopsys Design Compiler is used to analyze area, delay, and power for 32/28 nm standard cell.

The work [9] proposes a latest hardware productive reconfigurable FIR filter design based on the binary signed sub-coefficient approach. The requirements of hardware for multiplexer units is drastically decreased when compared to traditional techniques using proposed coefficient representation method. The proposed filter architecture's FPGA synthesis results indicate a significant reduction in resource consumption when compared to two previously published state-of-the-art reconfigurable architectures.

The study [10] describes a DA implementation of the hardware realization of LMS adaptive filter. For better appropriation, the proposed method uses coefficient-distributive DA in conjunction with an adaptive filter whose filter coefficients change over time. Moreover, the coefficient distributive DA will use a multiplexer structure and adder network to provide a multiplier-less digital filter for the suggested LMS adaptive filter that eliminates the need for a LUT. For hardware design, synthesis, and configuration onto an FPGA for real-time adaptive filtering experiments, the VHDL is utilized. Lastly, modelling and experimental data are shown to verify the feasibility of our suggested LMS adaptive filter.

Using a RAM(Random Access Memory) based LUT, the proposed technique [11] stores the combinations of input samples and filter weights using OBC. Because the routing of large order filter is simpler, substantial savings are realized. ASIC and FPGA synthesis demonstrates that the proposed design provides higher throughput while occupying less area and using less power. For instance, compared to the best available system, an adaptive filter with 32 taps using the suggested technique takes up over 20% less space and achieves a clock speedup of 12.63% for sub-filter with 2-taps.

Realizing two adaptive filters utilizing DA and serial implementation of LUT lowers the total expense of the proposed filter. The suggested filter uses a lot fewer registers and adders than the best current approach without the need for multiplexers in the LUT. The filter performs better at convergence when two step-sizes in orders of O (1/ N), wherein N is the filter order. As a result, it offers a low-complexity method for designing pipelined adaptive filters based on DA for better convergence. The proposed 16th order ADF with a base unit of 4th order occupies less room and uses less power than the existing methods [12].

The study [13] uses Distributed Arithmetic(DA) architecture to create a Finite Impulse Response(FIR) filter in an efficient manner. Using look-up tables, DA architecture is an effective method for multiplying and accumulating (MAC) or calculating the inner product. The direct way of implementing MAC in the absence of DA makes use of dedicated multipliers, which are quick but need a significant amount of hardware. The look-up tables are separated in order to conserve memory units. In DSP hardware design, DA can save up to 80% of the total area. The development of an eight-order FIR filter employing DA architecture is demonstrated in this work through VHDL coding, Model sim simulation, and MATLAB output comparison.

This paper [14] is a novel parallel approach based on look-ahead approaches for designing high speed DFE using pipelining of layered multiplexer loops. The DFE is a well-known effective method for reducing ISI in a variety of magnetic recording and communication systems. Nonetheless, the DFE's feedback loop places a cap on the fastest hardware implementation speed that may be achieved. More complicated hardware is needed for a simple parallel implementation. The proposed technique provides significant reduction in complexity of the hardware as compared to the traditional parallel six-tap DFE systems.

With SAED 90 nm technology, the suggested design is generated in the Synopsis design compiler tool using Verilog HDL coding to determine the area, power, minimum and maximum sampling frequencies, “area delay products” (ADPs), and “power delay products” (PDPs). In addition to making higher order filters easier to design and apply, the suggested adaptive filter has a far lower level of complexity than previous designs. The suggested design will take up 30% less space than the current architecture, according to the synthesis results. Furthermore, there's a 25% decrease in power consumption compared to block-based adaptive filters. In comparison to the current design architectures, the suggested design has significantly lower ADP and PDP. The suggested architecture is highly suited for software-defined radio, adaptive decision feed-back equalizers for eliminating inter-symbol interference and signal noise, hearing aids, and ECG signal analysis, among other signal processing application designs [15].

B. Throughput

It is the ratio of clock rate to the time required to process one sample i.e.,

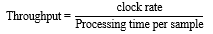
In [1], techniques such as unfolding and retiming is used to enhance the throughput. For 16-QAM, the suggested design delivers a throughput of almost 2.15 Gb/s.

The proposed architecture [2] for 16-QAM and 16th order FBF requires fewer iterations and improvements in error performance and throughput. The architecture is unfolded by a factor of 5 to increase the throughput.

In [16], a novel full-digital architecture for a wireline 2-level pulse amplitude modulation (2-PAM) system is proposed for the ADFB. The highest achievable speed in DFE is constrained by the feedback loop. The suggested plan starts with a fair assumption-based derivation of the coefficient-look ahead notion, from which a basic architecture can be developed utilizing the resulting formula. Moreover, the resulting formula can be made simpler based on the properties of the channel in order to break the feedback loop. Lastly, a high throughput rate can be attained by simply pipelining and processing the architecture in parallel. With a parallel and pipeline architecture, the suggested approach is hence fast. This paper introduces the implementation of a "built-in self-test" (BIST) circuit fabricated using TSMC 40nm CMOS technology. Based on the measured data, the circuit achieves a maximum throughput rate of up to 16 Gbps.

The study [17] suggests a pipelined decision-aided equalization approach with great performance. The feedforward filter comprises two miniature sub-filters employing the Adaptive Canceller Equalizer (ACE) architecture. One of these short filters combined with a tentative decision device will minimize the number of re-timing delays and enable usage of the tentative decision device's output will be input for the feedback filter. By doing this, the pipelined structure performs better while retaining throughput.

The study [18] presents an implementation of DFE using a multiplexer loop and a comparator array. The multiplexer loop's speed restricts the DFE's throughput. A new look-ahead calculation method for pipeline multiplexer loops is presented in this paper. The suggested method is illustrated and used to create DFEs based on multiplexer loops with throughput ranging from 3.125 to 10 Gbps.

The nonlinear decision-directed adaptation in DFE’s poses a challenge in achieving high speed. For the concurrent implementation of DFEs, recently proposed techniques include extended LMS DFE and parallel DFE. A new double-row DFE algorithm is described that performs better than the prior methods. The three aforementioned techniques require greater computing power and suffer from severe degradation at high speeds. This paper presents three more innovative parallel implementations of the DFE that avoid the coding loss of the previous approaches and result in significant hardware savings. The improved block approaches, double-row DFE without weight correction, and direct parallel algorithms are the names given to these novel algorithms.

When compared to the previous techniques, the first two algorithms' performance is just somewhat worse. The best performance is achieved at greater speeds using the improved block approach [19].

To reduce the decision feedback loop's iteration bound in the ADFB, this work uses the Predictive Parallel Branch slicer (PPBS) to remove dependencies between the decisions made in the past and present. Compared to the Relaxed Look-ahead ADFB architecture, the proposed architecture [20] can enhance the output mean-square error (MSE) of the ADFB by introducing minimal overhead associated with hardware complexity. Furthermore, it is demonstrated that the enhanced efficiency in terms of speed and SNR of the suggested pipelined ADFB using theoretical inferences and simulation outcomes.

In [21], Overflow is prevented in the updating weight calculations by placing an upper constraint on the algorithm step size, which is demonstrated to be lesser than the convergence bound. A specific dynamic scaling of the relevant input is implemented to prevent overflow occurrences at both the feedforward and feedback filter outputs. It is demonstrated that the suggested system, which mostly uses straightforward fixed-point operations, achieves a significant computational benefit over its counterpart based on floating points.

Partial precomputation schemes are the first method, which allows for a trade-off between computational performance and hardware complexity. The second strategy, a two-stage pre-computation scheme, is suitable for situations requiring more speed. Using second strategy, the hardware overhead and the iteration bound can be reduced. The suggested architectures are applied to ten Gbase-LX4 optical communication systems in order to illustrate their effectiveness [22].

This paper [23] suggests estimating the error probability in every iteration theoretically. The chance of error in the         DFFE(Decision Feed Forward Equalizer) is prone to approaching the DFE as the number of iterations grows. The DFFE method introduces a unique strategy to prevent the exponential growth in complexity, achieved through iterative cancellation of ISI using tentative decisions. The DFFE is a great option for the upcoming high-speed receiver generation because of these advantages.

C. Convergence

It is defined as the number of iterations required by an algorithm so that mean square error (MSE) reaches the optimum value. Mean square error is defined as the square on the difference between actual output and the estimated output

To reduce ISI, adaptive equalizers are needed for more speed, dependable data transmission over both wired and wireless time-dispersed communication channels. When the distortion in the channel surpasses the capacity of a linear equalizer, the non-linear ADFB proves to be highly beneficial. The system's high hardware cost creates a need to alter it to reduce the overall complexity of circuits and expense. This work presents ADFB employing LMS algorithms, based on pipelined CORDIC architecture. Better speed, throughput, and power efficiency with good convergence are the outcomes of the realization [24].

A new low-complexity Pipelined Decision Feedback RNN Equalizer (PDFRNE) is suggested. Since every module has a decision feedback structure and is a DFRNN(Decision Feedback Recurrent Neural Network), it can remove any residual past errors from the network. Furthermore, there is room for improvement in the performance. As its Infinite Impulse Response (IIR) structure, it can overcome instability [25].

In [26], the study compares various adaptive equalization algorithms and their performance is assessed using MATLAB simulation. The study also gives insights about neural networks for future generation communication networks. The research findings suggest that DNN-based neural network algorithms exhibit substantial potential and notable advantages in mitigating ISI in forthcoming endeavours. The comparison between different equalization algorithms is detailed in Table I.

This work [27] expands on a recently suggested method for constructing an adaptive filter to include an adaptive decision feedback equalization based on LMS. It is illustrated that adjusting the equalizer's weight update equation enables the attainment of a pipelined architecture, which delivers results directly at the initial stage and is latency free. The suggested solution gets around some of the drawbacks of the traditional techniques in that it doesn't require a compromise on convergence rate because there is no latency, which eliminates the need to use the delaying LMS algorithm for coefficient adaptation.

The results of this study [28] will enhance the convergence performance of CLS. The two algorithms that make up CLS(Cascaded Least Square) are Recursive Least Square (RLS) and Least Mean Square(LMS). While basic LMS is more user-friendly and less difficult than RLS, it does not achieve the same level of convergence as RLS. This study uses “Normalized Least Mean Square (NLMS) with training rate to address the shortcomings of the LMS method. According to this study, the training rate is a different approach that may be used to enhance CLS-DFE in wireless communication systems.

The primary task of an adaptive equalizer is to process the channel output with an unknown impulse response, aiming to approximate an ideal transmission medium when combined with the channel in cascade. In digital communications, adaptive equalizers typically undergo a training phase where a predefined data stream is transmitted.

During this phase, the equalizer coefficients are adjusted to align with the adaptive filtering technique utilized in its design, synchronizing with the transmitter at the receiver end. This study [29] offers an overview of contemporary adaptive equalization methodologies.

The study [30] compares the LMS with the fractional LMS method, demonstrating through experimental evidence that the fractional LMS algorithm exhibits a high convergence rate. Additionally, it has been noted that the LMS algorithm performs better for random signals, while fractional LMS has shown to be quite effective when dealing with deterministic signals. Eight channels with distinct tap weights are utilized in implementing these two algorithms in MATLAB

D. Challenges in 5G Communication

In order to investigate the resource allocation problem, this article categorizes the many 5G resource allocation systems that have been documented in the literature and evaluates how well they work to improve service quality. The debate in this poll is predicated on the parameters used to assess performance of the network. The review aims to enable scholars by recommending forthcoming research areas to focus on after taking into account the available evidence on allocation of resources strategies in 5G [31].

In [32] Global research efforts are being directed toward the development of a new technology that will be critical to the successful rollout of 5G. New technologies with high speed, capacity, energy efficiency, spectrum efficiency, pseudo-outside communication, etc. are being investigated to address any issues with the present mobile communication system. This article presents and describes a thorough analysis of the major technologies, difficulties, spectrum distribution, initiatives, and current 5G scenarios. The current study provides a thorough investigation to define the problems, and development along with 5G deployment.

This research [33] presents an updated overview of URLLC, focusing on the physical layer challenges and their resolution in 5G NR downlink. After defining the fundamental needs of URLLC, the physical layer issues and supporting technologies—such as scheduling techniques, packet and frame structure, and reliability enhancement tactics that have been addressed in the 3GPP Release 15 standard.          

The proposal [34] serves as a workable communication system intended to handle the ISI brought on by the additional Hilbert transform in the wireless environment as we move toward fifth generation (5G). This research suggests for the utilization of turbo code as an effective channel coding strategy for the 5G radio standard.

Based on the latest survey on the design of Adaptive Decision feedback equalizers, the summary is listed in Table II.

III. RESEARCH GAP

The present research advances significantly in optimizing adaptive decision feedback equalizers for high-speed communication systems and investigates URLLC in the 5G NR downlink. However, it also reveals potential avenues for further exploration.

A. Dynamic Channel Environments and Real-Time Adaptability

The study provides insights into diverse channel models, but there's a need for further investigation into the adaptability of proposed equalizers in dynamic and real-time channel variations. Focusing on scenarios involving fading, interference, and rapid changes could enhance the understanding of equalizer performance in unpredictable communication environments.

B. Enhanced Energy Efficiency

While power efficiency is considered, a more in-depth exploration of energy efficient implementations, especially in resource constrained environments, is warranted. Investigating novel techniques to optimize energy consumption without compromising performance would be valuable for practical applications.

C. Security Considerations in High-Speed Communication

The research does not explicitly address security aspects. Exploring the resilience of proposed equalizers against potential adversarial attacks or security breaches is crucial. Understanding how these equalizers fare in ensuring secure communication channels would be a significant extension.

D. Real-World Deployment Challenges and Standardization

Investigating the challenges associated with deploying advanced equalizers in real-world scenarios is essential. Taking into consideration factors such as hardware constraints, interoperability, and standardization will help to bridge the disparity between theoretical advancements and practical implementations.

Additionally, a comparative analysis with other state-of-the-art approaches and emphasizing benchmarking and standardization in the 5G landscape will contribute to a more holistic understanding of proposed methodologies.

Addressing these research gaps will not only   refine adaptive equalization techniques, but also ensure their practical efficacy in the face of evolving communication challenges and the dynamic landscape of 5G technology.

Conclusion

This study concludes with significant contributions to the optimization of communication systems, focusing on ADFB and URLLC in the 5G New Radio (NR) downlink. In ADFB design, leveraging distributed arithmetic and predictive parallel branch slicers leads to substantial advancements in convergence rates, throughput, and error performance. Strategies like pipelined decision-aided equalization and multifractal modeling address wireless communication challenges effectively. For URLLC in 5G NR, introducing turbo codes as a communication system proves promising in mitigating inter-symbol interference, an essential consideration for 5G success. The parallel design for high-speed Decision Feedback Equalizers (DFEs) offers not only hardware complexity reduction but also practicality and efficiency in evolving communication landscapes. Exploration of adaptive equalization techniques, especially using distributed arithmetic in ADFB designs, provides a hardware-efficient alternative with notable reductions in chip area and power consumption. These findings significantly contribute to advancing communication technologies, paving the way for the optimization of adaptive equalizers and URLLC in the dynamic 5G NR communication landscape.

References

[1] M. T. Khan and R. A. Shaik, \"An Energy Efficient VLSI Architecture of Decision Feedback Equalizer for 5G Communication System,\" in IEEE Journal on Emerging and Selected Topics in Circuits and Systems, vol. 7, no. 4, pp. 569-581, Dec. 2017. [2] M. T. Khan and R. A. Shaik, \"High-Throughput and Improved-Convergent Design of Pipelined Adaptive DFE for 5G Communication,\" in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 68, no. 2, pp. 652-656, Feb. 2021. [3] M. S. Prakash and R. A. Shaik, \"Low complexity hardware architectural design for adaptive decision feedback equalizer using distributed arithmetic,\" International Conference on Computer Systems and Industrial Informatics, Sharjah, United Arab Emirates, 2012, pp. 1-5. [4] Prakash, M. S., & Ahamed, S. R. (2021) “A Distributed Arithmetic based realization of the Least Mean Square Adaptive Decision Feedback Equalizer with Offset Binary Coding scheme” Signal Processing, 185, 108083. [5] D. J. Allred, Heejong Yoo, V. Krishnan, W. Huang and D. V. Anderson, \"LMS adaptive filters using distributed arithmetic for high throughput,\" IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 52, no. 7, pp. 1327-1337, July 2005. [6] Rui Guo and Linda S. DeBrunner, \"Two High-Performance Adaptive Filter Implementation Schemes Using Distributed Arithmetic,\" IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 58, no. 9, pp. 600-604, Sept. 2011. [7] M. S. Prakash and R. A. Shaik, \"Low-Area and High-Throughput Architecture for an Adaptive Filter Using Distributed Arithmetic,\" IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 60, no. 11, pp. 781-785, Nov. 2013. [8] S. Akhter, S. Kumar and D. Bareja, \"Design and Analysis of Distributed Arithmetic based FIR Filter,\" International Conference on Advances in Computing, Communication Control and Networking (ICACCCN), Greater Noida, India, 2018, pp. 721-726. [9] A. Abbaszadeh, A. Azerbaijan and K. D. Sadeghipour, \"A new hardware efficient reconfigurable fir filter architecture suitable for FPGA applications,\" 17th International Conference on Digital Signal Processing (DSP), Corfu, Greece, 2011, pp. 1-4. [10] A. Trakultritrung, E. Thanangchusin and S. Chivapreecha, \"Distributed arithmetic LMS adaptive filter implementation without look-up table,\" 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Phetchaburi, Thailand, 2012, pp. 1-4, [11] M. T. Khan and S. R. Ahamed, \"A New High Performance VLSI Architecture for LMS Adaptive Filter Using Distributed Arithmetic,\" IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Bochum, Germany, 2017, pp. 219-224. [12] M. T. Khan and S. Rafi Ahamed, \"Enhanced Convergence Distributed Arithmetic based LMS Adaptive Filter using Convex Combination,\" Twenty Fourth National Conference on Communications (NCC), Hyderabad, India, 2018, pp. 1-6. [13] Chandan Singh, \"Realization of FIR Filter using Distributed Arithmetic Architecture,\" International Journal of Scientific Research in Computer Science and Engineering, Vol.3, Issue.4, pp.7-12, 2015 [14] D. Oh and K. K. Parhi, \"Low Complexity Design of High Speed Parallel Decision Feedback Equalizers,\" IEEE 17th International Conference on Application-specific Systems, Architectures and Processors (ASAP\'06), Steamboat Springs, CO, USA, 2006, pp. 118-124. [15] Vijetha, K., & Rajendra Naik B. (2022). “Low power low area VLSI implementation of adaptive FIR filter using DA for decision feedback equalizer” Microprocessors and Microsystems, 93, 104577. [16] W. -Q. He, Y. -C. Lin, J. -Y. Hung and S. -J. Jou, \"Full-digital high throughput design of adaptive decision feedback equalizers using coefficient-lookahead,\" 2015 IEEE 11th International Conference on ASIC (ASICON), Chengdu, China, 2015, pp. 1-4. [17] Inseop Lee and W. K. Jenkins, \"Pipelined implementation of the adaptive canceller-equalizer,\" ISCAS (IEEE International Symposium on Circuits and Systems ) (Cat. No.01CH37196), Sydney, NSW, 2001, pp. 76-80 vol. 4. [18] K. K. Parhi, \"Pipelining of parallel multiplexer loops and decision feedback equalizers,\" 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 2004, pp. V-21 [19] K. J. Raghunath and K. K. Parhi, \"Parallel adaptive decision feedback equalizers,\" [Proceedings] ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 1992, pp. 353-356 vol.4, [20] Meng-Da Yang, An-Yeu Wu and Jyh-Ting Lai, \"High-performance VLSI architecture of adaptive decision feedback equalizer based on predictive parallel branch slicer (PPBS) scheme,\" IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 12, no. 2, pp. 218-226, Feb. 2004. [21] Shaik, R. A., & Chakraborty, M. (2013) “A block floating point treatment to finite precision realization of the adaptive decision feedback equalizer” Signal Processing, 93(5), 1162-1171. [22] C. . -H. Lin, A. . -Y. Wu and F. . -M. Li, \"High-Performance VLSI Architecture of Decision Feedback Equalizer for Gigabit Systems,\" IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 53, no. 9, pp. 911-915, Sept. 2006 [23] Pola, A. L., Cousseau, J. E., Agazzi, O. E., & Hueda, M. R. (2013) “A Low-Complexity Decision Feedforward Equalizer Architecture for High-Speed Receivers on Highly Dispersive Channels” Journal of Electrical and Computer Engineering, 2013(587108) [24] R. Mishra and A. Mandal, \"Coordinate rotation algorithm based non-linear Adaptive Decision Feedback Equalizer,\" International Multi-Conference on Systems, Signals & Devices, Chemnitz, Germany, pp. 1-5 [25] H. Zhao, X. Zeng, J. Zhang and T. Li, \"Nonlinear Adaptive Equalizer Using a Pipelined Decision Feedback Recurrent Neural Network in Communication Systems,\" IEEE Transactions on Communications, vol. 58, no. 8, pp. 2193-2198, August 2010. [26] Zichen Xi \"Analysis of Adaptive equalization algorithms,\" Highlights in Science, Engineering and Technology ICMEA 2023 vol.70. [27] Chakraborty, M., & Pervin, S. (2003) “Pipelining the adaptive decision feedback equalizer with zero latency” Signal Processing, 83(12), 2675-2681. [28] Sulong, S. M., Idris, A., & Ali, D. M. (2020) “Enhancement of LMS Convergence Rate with CLS-DFE for 5G Wireless Communication System” International Conference on Technology, Engineering and Sciences (ICTES) 2020 (IOP Conf. Series: Materials Science and Engineering 917, 012079). IOP Publishing. [29] Garima Malik and Amandeep Singh Sappal, “Adaptive Equalization Algorithms: An Overview” International Journal of Advanced Computer Science and Applications (IJACSA), 2(3), 2011. [30] Mahmood, L., Shirazi, S. F., Naz, S., Shirazi, S. H., Razzak, M. I., Umar, A. I., & Ashraf, S. S. (2015) “Adaptive Filtering Algorithms for Channel Equalization in Wireless Communication” Indian Journal of Science and Technology, 8(17). [31] Kamal, M. A., Raza, H. W., Alam, M. M., Su’ud, M. M., & Sajak, A. A. B. (2021) “Resource Allocation Schemes for 5G Network: A Systematic Review” Sensors, 21(19), 6588. [32] Kumar, A., & Gupta, M. (2018). “A review on activities of fifth generation mobile communication system” Alexandria Engineering Journal, 57(2), 1125-1135. [33] H. Ji, S. Park, J. Yeo, Y. Kim, J. Lee and B. Shim, \"Ultra-Reliable and Low-Latency Communications in 5G Downlink: Physical Layer Aspects,\" IEEE Wireless Communications, June 2018 vol. 25, no. 3, pp. 124-130. [34] Alhasani, M. M., Nguyen, Q. N., Ohta, G.-I., & Sato, T. (2019). A Novel Four Single-Sideband M-QAM Modulation Scheme Using a Shadow Equalizer for MIMO System toward 5G Communications. Sensors, 19, 1944.

Copyright

Copyright © 2024 Venkatesha G, Vijaya Kumar C N, Hema C. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.