Estimation of Transverse Shear Stresses across the Thickness of Three-Layered Orthotropic Sandwich Plates Using ABAQUS

Abstract

This paper primarily focuses on presenting the results obtained through ABAQUS Finite Element Modelling (FEM) tool. These findings have been subjected to a comparative analysis with both the 3D exact elasticity solutions and the partial FEM solutions. Notably, the ABAQUS results, as described in reference demonstrate a remarkable level of accuracy, particularly in relation to transverse shear stresses. It is crucial to underscore that the principal objective of this research revolves around the precise determination of transverse shear stresses, as these have been identified as potential contributors to delamination within the studied structures. It can be asserted that the objectives, cantered on the accurate computation of transverse shear stresses, have been successfully achieved through the implementation of ABAQUS Finite Element modelling.

Introduction

I. INTRODUCTION

Sandwich structures, often referred to as composite sandwich panels, represent a class of engineered materials widely used in various industries, including aerospace, automotive, marine, construction, and more.

These structures consist of two outer skins (face sheets or laminates) bonded to a lightweight core material, creating a layered or sandwich-like configuration.

The combination of different materials in a sandwich structure results in a composite material with unique mechanical, thermal, and acoustic properties.

The analysis of sandwich structures presents several complex challenges due to their multifaceted nature and the interaction between different components. Some of the key challenges in the analysis of sandwich structures include:

1. Material Heterogeneity: Sandwich structures often involve materials with vastly different properties, such as composite face sheets and lightweight core materials. Modeling the behavior of these heterogeneous materials accurately is essential for predicting overall structural performance.
2. Three-Dimensional Effects: In many practical applications, sandwich structures exhibit three-dimensional deformation behavior, especially in curved or complex geometries. Analyzing these structures in three dimensions requires advanced numerical techniques and computational resources.
3. Delamination and Debonding: Delamination between the face sheets and core is a critical issue in sandwich structures. Detecting and predicting delamination and debonding is crucial for assessing structural integrity and durability.
4. Load Distribution: The distribution of loads between the face sheets and the core is not always uniform. An accurate analysis should consider load transfer mechanisms, such as shear and bending, within the sandwich structure.
5. Failure Modes: Sandwich structures can fail in various modes, including buckling, local indentation, fatigue, and impact. Understanding the modes of failure and developing strategies to mitigate them is essential for designing robust structures.
6. Nonlinear Behavior: Many sandwich structures exhibit nonlinear behavior, particularly when subjected to large deformations, high loads, or temperature variations. Nonlinear analyses may be required to capture this behavior accurately.
7. Environmental Effects: Sandwich structures can be sensitive to environmental conditions such as moisture absorption, temperature changes, and exposure to chemicals. These factors can affect material properties and structural performance.
8. Manufacturing Variability: Variations in material properties and manufacturing processes can lead to uncertainties in the structural response of sandwich structures. Statistical methods and probabilistic analysis techniques may be necessary to account for these uncertainties.

Sandwich structures offer numerous advantages in terms of lightweight design, strength, and versatility. However, their complex nature and the challenges necessitate advanced analysis methods, including experimental testing and computational simulations, to ensure their reliable performance in various applications. Researchers and engineers continue to work on developing innovative solutions and improving the understanding of these structures to address these challenges effectively. Some important review papers are listed below.

The comprehensive review presented by Noor et al.  [1] investigates computational models for sandwich plates and shells, emphasizing hierarchy, predictor-corrector procedures, and the influence of geometric and material variations on sandwich response. It covers various application areas, including heat transfer, mechanical stresses, vibrations, buckling, large deflections, damage, and optimization, referencing over 800 relevant sources. The review includes extensive numerical analysis of thermally stressed sandwich panels, assessing the impact of parameter changes on free vibration responses and sensitivity coefficients using eight modeling approaches. Analytic three-dimensional thermos elasticity solutions serve as a comparison benchmark. The article concludes by suggesting future research directions in sandwich plate and shell modeling. Numerous review articles have been published concerning the free vibration and buckling behavior of laminated composites, sandwich plates, and shells. Kumar and Srinivasa [2] provides an extensive overview of the existing literature related to the buckling and free vibration analysis of shear deformable isotropic and laminated composite sandwich plates and shells. It encompasses a comprehensive examination of the diverse methodologies that have been utilized for plate analysis in recent decades. The literature covers a wide spectrum, including various theories, finite element modeling, and experimental studies for the analysis of sandwich plates and shells. Additionally, the review incorporates select papers on topics such as functionally graded material plates, plates featuring smart skin technologies (electrorheological, magnetorheological, and piezoelectric), and even viscoelastic materials. Furthermore, the article assesses the potential directions for future research in the domain of sandwich plates and shells. The paper [3] highlights the significant challenge of solving complex geometric problems using plate and shell theories, resulting in numerous attempts to simplify three-dimensional issues. The growing use of laminated and sandwich structures necessitates higher accuracy from two-dimensional formulations. In the literature, various bi-dimensional theories and solution methods are available for tackling these problems, often categorized by how they handle variables in the normal direction of the plate/shell surface, such as equivalent single layer, Zig-Zag, and layer-wise theories. This paper contributes by reviewing over 100 papers and setting the stage for new theories and solution methods for laminated and sandwich structures. It provides a comprehensive overview of plate/shell theories and their corresponding solution methods, emphasizing the crucial coupling between the two. The study [4] extensively evaluates various plate theories for analyzing the bending and vibration of sandwich structures, focusing on classical, higher-order, zigzag, layerwise, and mixed theories. The assessment includes numerical analysis of simply supported orthotropic panels subjected to transverse bisinusoidal pressure distribution. Results emphasize the importance of considering length-to-thickness-ratio (LTR) and face-to-core-stiffness-ratio (FCSR) parameters in accuracy evaluations. Higher-order theories (HOTs) are effective in reducing LTR-related errors in thick plates, while layerwise analysis is essential for addressing errors caused by increasing FCSR values in classical theory analysis. A comprehensive review is conducted [5] on computational approaches for analyzing laminated composite and sandwich panels, encompassing over two hundred texts. The review primarily explores theoretical models for multilayered plates and shells and the finite element method's (FEM) implementation of computational concepts. The findings reveal a need for a single numerical model capable of universally representing all layered composite and sandwich panels. Additionally, it suggests that as the range of rotations considered in a specific model increases, the complexity of through-the-thickness deformation profile representation tends to decrease.

A comprehensive bibliographical review was conducted [6] on finite element analyses of sandwich structures, covering both theoretical and practical aspects. It encompasses isotropic and composite materials, addressing various topics like material properties, vibration, dynamics, heat transfer, contact, fracture mechanics, stability, special finite elements, and applications in engineering. In another review [7] which focuses on composite models, predictor-corrector procedures, temperature-dependent material properties, and sensitivity analysis for thermomechanical responses. It covers eight application areas, including heat transfer, thermal stresses, curing, buckling, vibrations, deflection, and sandwich structures. The study presents extensive numerical results, demonstrating how variations in lamination and geometric parameters affect the thermal buckling response in temperature-sensitive angle-ply composite plates. Nine modeling approaches are compared to exact three-dimensional thermoelasticity solutions. The review concludes by outlining potential research directions for high-temperature multilayered composites. The increasing use of composite structures due to their superior strength-to-weight ratios, emphasizing the need for accurate theoretical and finite element analysis of sandwich plates in design.

The paper [8] reviews recent research trends in finite element formulations, particularly those developed after 2000, covering various theories and models, including shear deformation, solid-shell elements, and piezoelectric structures, with a focus on buckling analysis. Twenty distinct theories for analyzing multilayered plates are reviewed [9]. The mathematical formulation considers the nonlinear kinematics of a mechanically loaded plate using von Karman theory. To solve the resulting nonlinear equilibrium equations, a quadratic extrapolation technique is employed to linearize them. The study utilizes a meshfree approach based on polynomial radial basis functions to obtain solutions. Validation of the results for the sandwich plate against other available data reveals that certain theories significantly underestimate deflection. Additionally, the paper explores the impact of varying core thickness on the stresses and deflection of the sandwich plate. In the article [10] provides an overview of three-dimensional (3D) analytical approaches for analyzing multilayered and functionally graded (FG) piezoelectric plates and shells. It categorizes these approaches into four types: Pagano's classical, state space, series expansion, and asymptotic approaches. The article derives both mixed and displacement-based formulations for 3D analysis of multilayered piezoelectric plates and briefly explains the analytical process for each approach. These formulations can also be applied to FG piezoelectric plates by treating them as layered plates with constant coefficients. The article includes a comprehensive comparison of 3D results from various approaches and presents through-thickness distributions of field variables for simply-supported multilayered and FG piezoelectric plates. It also surveys relevant literature on 3D analysis in this context. The review paper [11] provides a comprehensive review of research conducted between 2000 and 2010 on the static and buckling behavior of composite shells, including postbuckling analysis. The review focuses on the types of analysis performed, considering complications arising from both material (e.g., piezoelectric) and structural factors (e.g., stiffened shells), and examines various shell geometries such as cylindrical, conical, and spherical shapes. Additionally, the paper pays attention to the theories applied, including thin, thick, 3D, and nonlinear approaches. The paper [12] presents a historical overview of theories developed for the analysis of multilayered structures, with a specific focus on Zig-Zag theories. These theories describe a discontinuous displacement field in the thickness direction of plates and shells while maintaining continuity of transverse stresses at layer interfaces. The review primarily addresses plate and shell geometries, occasionally including beams. It emphasizes models where the number of displacement variables remains independent of the number of constitutive layers. The discussion centers on theories based on the method of hypotheses or axiomatic approaches, involving assumptions related to displacements and transverse stresses. Scientists discovered various higher order shear deformation theories for precise estimation of interlaminar shear stress. The paper [13] introduces analytical formulations and solutions for the stability analysis of simply supported composite and sandwich plates. These formulations are based on a higher order refined theory, which accounts for transverse shear deformation, transverse normal strain/stress, and a nonlinear variation of in-plane displacements. This theory provides a more accurate representation of transverse cross-section warping and eliminates the need for shear correction coefficients. Equilibrium equations are derived using the Principle of Minimum Potential Energy. Comparative analysis with existing elasticity solutions and other higher order theories demonstrates that this refined theory offers more precise predictions of critical buckling loads. Additionally, new results for sandwich laminates are presented, serving as benchmarks for future research. This paper [14] presents novel analytical formulations and solutions for the static analysis of simply supported composite and sandwich plates. These formulations are based on a higher order refined theory that incorporates laminate deformations, accurately modeling transverse shear deformation, transverse normal strain/stress, and nonlinear variations of in-plane displacements. This eliminates the need for shear correction coefficients. The study also considers a few other higher order theories and a first-order theory from existing literature for comparison. Equilibrium equations are derived using the Principle of Minimum Potential Energy, and solutions are obtained in closed form using Navier's technique. Comparison with existing elasticity solutions and other theories demonstrates that this refined theory provides more accurate predictions of transverse displacement and stresses. The paper also presents new results for the stretching–bending coupling behavior of antisymmetric sandwich laminates, serving as a benchmark for future research. This study [15] introduces a novel higher order analysis model for sandwich plates with flexible cores, particularly soft cores. It derives governing equations from equilibrium differential equations of motion and provides analytical solutions for simply supported sandwich plates with flexible cores. The solutions cover free vibration analysis and static bending under sinusoidal and uniformly distributed loads. The accuracy and convergence of this theory and solution are verified by comparing them with various existing results, considering different parameters like length-to-width ratios, Young's modulus ratios, thickness ratios, and span-to-thickness ratios of sandwich plates. The study demonstrates that this theory achieves high accuracy in comparison to classical plate theory, first-order shear deformation, higher order shear deformation theory, and finite element software ANSYS for sandwich plates with flexible cores.

This paper [16] addresses local stress concentrations in sandwich structures, particularly around inserts in structural sandwich plates.

It introduces a high-order theory specifically designed for studying sandwich plates with inserts, considering the transverse flexibility of the core material. The theory includes descriptions of face sheets and core materials, along with various load and boundary conditions. Numerical solutions are obtained using the "multi-segment method of integration," and examples involving sandwich plates with inserts under different load conditions are provided. The paper concludes with a discussion of design considerations for such structures. This study [17] introduces a new model based on high-order sandwich panel theory to analyze the impact of external loads on the free vibration and buckling of circular cylindrical composite sandwich shells with a transversely compliant core. Unlike many existing theories, this model doesn't make prior assumptions about the core's displacement field, determining it through a 3D elasticity solution. Comparative results for various material properties and geometric parameters demonstrate the model's high accuracy. It is suggested that this model, serving as a benchmark, can guide future research on the free vibration and buckling of such sandwich shells with a transversely compliant core. This study [18] presents an improved higher-order theory for analyzing the stress in laminated transversely isotropic plates and shells subjected to transverse shear deformation and normal compression. The theory accommodates layered structures with varying physical and mechanical properties. It introduces new physically meaningful variables and considers various loading and boundary conditions to account for transverse shear and normal reduction. Closed-form solutions for some multilayered plates and shells are provided and validated against existing literature. The paper discusses the theory's features and the implications of its numerical results. This paper [19] introduces a refined higher-order shear deformation theory for analyzing the bending, vibration, and buckling of functionally graded sandwich plates. The theory incorporates only four unknowns, considers a hyperbolic distribution of transverse shear stress, and satisfies traction-free boundary conditions. Equations of motion are derived using Hamilton's principle, and both Navier-type and finite element solutions are provided for plates with different boundary conditions. Numerical examples are presented for functionally graded sandwich plates with various core types, demonstrating the theory's accurate and efficient predictive capabilities. This paper [20] introduces a unified mixed, higher-order analytical formulation for predicting general buckling and wrinkling in multi-layer, multi-core sandwich plates with arbitrary layer and core sequences. Unlike traditional assumptions, it eliminates the need for thin stiff layers and anti-plane cores. The formulation enforces displacement and transverse stress continuities as degrees of freedom and directly computes modal transverse stresses as eigen vectors, avoiding separate calculations. Two sets of mixed models, based on individual layers and equivalent single layer (ESL) theories, are proposed. Results align well with three-dimensional elasticity solutions and experimental data, highlighting the limitations of ESL theories and simplifying assumptions. This study [21] presents the response of a sandwich panel with bilinear shear stress behavior in the core using an improved extended high-order sandwich panel theory. The theory employs the first-order shear deformation theory for the face sheets and two-dimensional elasticity for the core. Ritz-based solutions are used for various boundary conditions. The effects of the core's plastic shear modulus on shear stress distribution, transverse normal stresses, displacement components, force and moment resultants, and transverse displacements are examined. Results show the presence of initial plastic regions at core edges, with lower shear stresses in the plastic zones compared to linear elastic analysis. The extent of plastic regions is more significant in simply supported cases than in clamped edges. Additionally, the study compares results of transverse deflections and shear stresses with finite element simulations in the case of linear elastic analysis. This paper [22] introduces a nonlinear high-order theory for cylindrical sandwich shells with flexible cores, building upon a previously developed high-order theory for sandwich plates. The theory accounts for relatively thin outer and inner faces compared to the core and addresses core compressibility effects. It derives governing equations and boundary conditions using a variational principle. Numerical results are presented for cases with orthotropic materials, demonstrating the model's ability to capture nonlinearity in transverse stress distribution within the core. The study provides valuable insights for optimizing the design of advanced cylindrical sandwich shells. Review of selected Zig Zag theories are discussed below.

The paper [23] investigates the free vibration response of sandwich curved and flat panels by incorporating the zig-zag function (ZZF) into classical and higher-order two-dimensional shell theories' displacement models. ZZF introduces a zig-zag effect in the displacement distribution at core/faces interfaces. The study compares results with and without ZZF, considering various face-to-core stiffness ratios and geometric parameters. It concludes that ZZF is highly recommended for free vibration analysis of sandwich plates and shells, as it reduces errors and is easy to implement compared to other refined theories. The paper [24] highlights the benefits of incorporating the zig-zag function (ZZF) into the bending analysis of sandwich flat panels. It develops higher-order theories by adding ZZF to displacement fields of established theories. ZZF introduces a zig-zag effect in the first derivative of displacement distribution at core-face interfaces. The study compares results with and without ZZF for sandwich plates with a soft core subjected to harmonic transverse pressure. Various face-to-core stiffness ratios (FCSR) and length-to-thickness ratios (LTR) are considered. The conclusions are: (1) ZZF is highly recommended for sandwich plate bending analysis; (2) using ZZF reduces errors and makes them less dependent on the FCSR parameter; (3) ZZF is easy to implement and preferable over other refined theories.

In the paper [25], the study focuses on circular/annular sandwich plates consisting of orthotropic composite face sheets and auxetic (with negative Poisson's ratio) cores. They employ a zigzag theory to determine lateral deflections, in-plane normal and transverse shear stresses. The results are then corrected using the three-dimensional theory of elasticity. The governing equations are developed based on the principle of minimum total potential energy and solved using a differential transform method. The study conducts a comprehensive parametric analysis considering various geometric and material parameters, lamination schemes, and boundary conditions. The accuracy of the results is confirmed by comparing them with 3D theory of elasticity results from the ABAQUS code. The findings indicate that core auxeticity significantly enhances the core's rigidity, reducing lateral deflection and moderating interfacial jumps in transverse shear stress distribution. This effect is more pronounced in plates with rigid constructions or specific boundary conditions. The study [26] refines a finite element model based on an improved higher-order zigzag plate theory. The theory is applied to analyze the bending and vibration responses of soft core sandwich plates. It satisfies interlayer transverse shear stress continuity, including transverse shear stress-free conditions at the top and bottom surfaces of the plate, as well as transverse normal compressibility of the core. The in-plane displacements vary cubically through the entire thickness, while transverse displacement is assumed to vary quadratically within the core. The study adopts a C0 finite element formulation and refines it using a penalty function approach to meet certain constraints. The model's performance is validated by comparing its results with 3D elasticity solutions and other available data. The paper [27] focuses on the axisymmetric bending and stress analysis of circular functionally graded sandwich plates under transversely distributed loads. The analysis employs an elasticity-equilibrium-based zigzag theory, which considers local variations of the displacement field and satisfies continuity conditions of transverse stresses at layer interfaces. The governing equations are solved using a semi-analytical Maclaurin-type power-series solution. The layers of the plate can be made of functionally graded materials. The results are compared to those obtained from a numerical finite element code (ABAQUS software), showing that the proposed formulation provides accurate results even for thick sandwich plates with soft cores, comparable to the three-dimensional theory of elasticity. The paper [28] explores the analysis of sandwich laminates, where core and skin materials have distinct properties, utilizing a layerwise approach. The study focuses on the static and free vibration analysis of sandwich plates using collocation with radial basis functions and a novel layerwise theory that allows for independent rotations in each layer and thickness stretching. This formulation enables accurate computation of transverse normal and shear deformations and stresses. The equations of motion were automatically implemented through a Unified Formulation and interpolated using radial basis functions. The paper includes examples involving composite laminated plates and sandwich plates, with the results discussed and examined. The paper [29] introduces a layerwise finite element approach for dynamic analysis of functionally graded material (FGM) sandwich shells under both thermal and non-thermal conditions. The layerwise theory employed is based on the first-order shear deformation theory (FSDT) and ensures displacement continuity at layer interfaces. Two FGM sandwich shell configurations are examined: one with FGM facesheets and a homogeneous core, and the other with homogeneous facesheets and an FGM core. Effective material properties for the FGM are determined using two micromechanical models, Voigt's rule of mixture (ROM) and Mori-Tanaka (MT) scheme. The study also considers shells subjected to non-uniform temperature distributions across their thickness, with temperature-dependent elastic properties. Results obtained from the proposed approach are compared with existing literature for validation. Additionally, the paper investigates the natural frequencies of FGM sandwich shells under varying conditions such as volume fraction index, core thickness, and temperature gradient. The formulation presented in this paper is characterized by its simplicity, accuracy, and computational efficiency. The study [30] addresses the critical importance of lightweight sandwich materials in various engineering applications, such as aerospace, marine, and packaging. Foam core sandwich materials are favored for their lightweight properties and exceptional thermal insulation capabilities. They find use in marine vehicle construction (e.g., boats, yachts), sporting goods (e.g., surfboards), and even in NASA spacecraft for impact absorption and thermal insulation. To meet the demand for high-fidelity analysis tools for sandwich materials, the research presents a three-layer approach using refined higher-order plate theory for each of the three layers in a sandwich plate. The analysis accounts for the compressibility (thickness strain) of the central core layer and ensures the continuity of displacements and stresses at each layer interface through a Lagrangian multiplier approach. The formulated theory is implemented in a custom Fortran code. It is applied to analyze various polymer composite and sandwich plates, demonstrating that the results correlate well with reliable published data across different plate aspect ratios and ply orientations. This research offers valuable insights into the behavior of sandwich plates and provides a robust analytical tool for engineering applications. Few review on 3D elasticity solution is presented below.

Tornabene and Brischetto [31] conducted a comparative investigation involving various analytical and numerical models, both three-dimensional (3D) and two-dimensional (2D), to analyze the bending behavior of composite and sandwich plates, as well as spherical and doubly-curved shells. The analysis focuses on the response to a transverse normal load applied to the upper surface.

In space structures, sandwich shells with fiber-reinforced plastic laminated sheets are frequently used. To better describe their behavior and connect them with 3D brick elements, a novel 32-node, three-layer shell element with relative degrees of freedom is introduced [32] using 3D Finite Element Modeling (FEM). Additionally, a post-processing technique is proposed to accurately compute transverse shear and normal stresses in laminated shells of revolution, eliminating stress discontinuities and satisfying load boundary conditions.

The new study [33] introduces a precise three-dimensional static analysis approach for plates and shells. It examines single-layered and multi-layered structures with various properties, including isotropic, orthotropic, sandwich, and composite materials, considering displacements and stresses in both in-plane and out-of-plane directions across the thickness. The structures in question are assumed to be fully supported and subjected to a transverse normal load. The method's foundation lies in utilizing 3D equilibrium equations formulated with general orthogonal curvilinear coordinates, which are applicable to spherical shells. Additionally, this method provides results for cylindrical shells, cylinders, and plates as specific cases derived from the 3D spherical shell equations. Importantly, this analysis avoids any geometrical approximations when assessing the mentioned structures. Many researchers used FEM tool ABAQUS in the analysis of sandwich structures. In the study, [34] which examines the impact of polymeric foam filling on the vibrational and buckling characteristics of sandwich plates featuring a hexagonal honeycomb core. In real-world applications of honeycomb sandwich structures, a common issue is debonding at the interface between the face sheets (skins) and the core.

Introducing foam into honeycomb cores can enhance resistance to debonding but also alters the structural behavior of the sandwich structure. To assess the influence of polymeric foam, the researchers conducted analyses using the ABAQUS finite element code. They modeled the sandwich plates with both hollow and foam-filled honeycomb cores, employing simplified three-layered continuum models.

The study utilized the finite element method and a displacement-based homogeneous technique to determine the effective elastic properties of the core in both configurations. The results provide comparisons of load-carrying capacities and natural frequencies between the two types of sandwich plates, shedding light on the structural advantages of foam-filled sandwich plates. The study investigates the buckling behavior of Nomex honeycomb core sandwich panels with glass-epoxy face sheets. These panels are commonly used in industries such as marine, aerospace, automotive, and shipbuilding due to their high strength-to-weight ratio and excellent energy absorption properties.

The research focuses on both bare honeycomb cores and those filled with foam, considering the viscoelastic properties of the sandwich panel. The viscoelastic properties of the composite face sheets and foam are determined through relaxation tests and implemented in ABAQUS [35] using VUMAT code. The finite element method is employed with ABAQUS to model the buckling behavior of the sandwich panels, taking into account both elastic and viscoelastic material behavior. The study explores various factors, including composite face sheet lay-up, core thickness, core cell size, and foam filling, to evaluate their effects. Both experimental and numerical results indicate that foam filling increases the critical buckling load and enhances energy absorption in the sandwich panels.

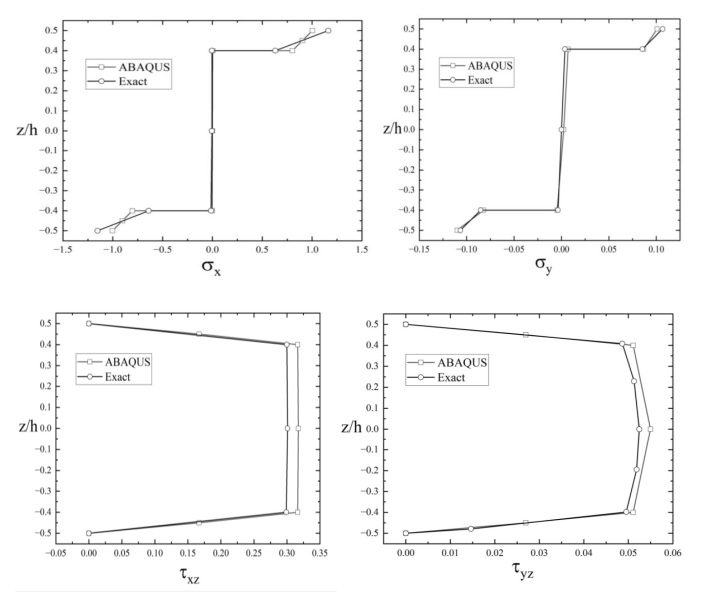
In this paper, the outcomes derived through ABAQUS Finite Element Modeling (FEM) are presented for layered orthotropic sandwich plates. These results have been compared with the 3D exact elasticity solutions presented and with the partial FEM solutions. The ABAQUS [36] results exhibit a notably low percentage of error, particularly in the context of transverse shear stresses. It's important to highlight that the primary aim of this research is to accurately determine the transverse shear stresses, as these are identified as potential contributors to delamination. In this regard, ABAQUS approaches yield satisfactory outcomes. To provide a comprehensive view of the outcomes across the thickness, we have presented the ABAQUS results which encompass in-plane normal stresses and transverse shear stresses. In conclusion, it can be affirmed that the research objectives pertaining to the precise calculation of transverse shear stresses have been successfully met.

II. NUMERICAL RESULTS

Example: Three layered (00/CORE/00) Orthotropic Sandwich plates subjected to doubly sinusoidal mechanical loading.

In this example, the results from from ABAQUS FEM modelling are compared with 3D exact elasticity solutions by Pagano [37] and by partial FEM solutions given by Kant et al. [38] and mixed FEM [39]. Table 1 shows the normalized deflection and stresses in sandwich plate subjected to sinusoidal mechanical loading for aspect ratios 4, 10, 20 and 100. Present ABAQUS reports low % error as especially in transverse shear stresses as 1.86 %. The objective of this research is to obtain accurately the transverse shear stresses which are causing delamination is therefore gives satisfactory results from ABAQUS. Across the thickness results from ABAQUS are presented in Figs. 1 to 5 for in plane normal stresses and transverse shear stresses.

III. ACKNOWLEDGEMENTS

This research work (Project No: 188) is supported under the research grant provided by Indian Space Research Organization (ISRO) and Savitribai Phule Pune University (SPPU) Technology Cell, Pune.

Conclusion

In conclusion, the current Finite Element Modeling (FEM) approach using ABAQUS has proven to provide an accurate representation of the stresses and displacements within the sandwich structure.

References

[1] Noor, A. K., Burton, W. S., & Bert, C. W. (1996). Computational Models for Sandwich Panels and Shells. Appl. Mech. Rev., 49(3), 155–199. https://doi.org/10.1115/1.3101923 [2] Kumar, P., & Srinivasa, C. (2020). On buckling and free vibration studies of sandwich plates and cylindrical shells: A review. J Thermoplast Compos Mater, 33(5), 673-724. doi:10.1177/0892705718809810 [3] Mauricio F. Caliri, Antonio J.M. Ferreira, Volnei Tita, A review on plate and shell theories for laminated and sandwich structures highlighting the Finite Element Method, Composite Structures, 156, 63-77. https://doi.org/10.1016/j.compstruct.2016.02.036. [4] Carrera, E., & Brischetto, S. (2008). A Survey With Numerical Assessment of Classical and Refined Theories for the Analysis of Sandwich Plates. Appl. Mech. Rev., 62(1), 010803. https://doi.org/10.1115/1.3013824 [5] Kreja, I. (2011). A literature review on computational models for laminated composite and sandwich panels. Open Engineering, 1(1), 59-80. https://doi.org/10.2478/s13531-011-0005-x [6] Mackerle, J. (2002). Finite element analyses of sandwich structures: a bibliography (1980–2001). Eng. Comput., 19(2), 206-245. https://doi.org/10.1108/02644400210419067 [7] Noor, A. K., & Burton, W. S. (1992). Computational Models for High-Temperature Multilayered Composite Plates and Shells. Appl. Mech. Rev., 45(10), 419–446. https://doi.org/10.1115/1.3119742 [8] Shehzaib IRFAN, Faisal SIDDIQUI. (2019). A review of recent advancements in finite element formulation for sandwich plates. Chinese Journal of Aeronautics, 32(4), 785-798. https://doi.org/10.1016/j.cja.2018.11.011. [9] Solanki, M. K., Mishra, S. K., & Singh, J. (2016). Meshfree approach for linear and nonlinear analysis of sandwich plates: A critical review of twenty plate theories. Eng. Anal. Bound. Elem., 69, 93-103. https://doi.org/10.1016/j.enganabound.2016.05.002 [10] Wu, C., Chiu, K., & Wang, Y. (2008). A review on the three-dimensional analytical approaches of multilayered and functionally graded piezoelectric plates and shells. Comput. Mater. Continua, 8(2), 93–132 [11] M. Qatu, E. Asadi, & W. Wang. (2012). Review of Recent Literature on Static Analyses of Composite Shells: 2000-2010. Open Journal of Composite Materials, 2(3), 61-86. doi: 10.4236/ojcm.2012.23009 [12] Carrera, E. (2003). Historical review of Zig-Zag theories for multilayered plates and shells. ASME. Appl. Mech. Rev., 56(3), 287-308. https://doi.org/10.1115/1.1557614 [13] Kant, T., & Swaminathan, K. (2000). Analytical solutions using a higher-order refined theory for the stability analysis of laminated composite and sandwich plates. Structural Engineering and Mechanics, 10(4), 337–357. https://doi.org/10.12989/SEM.2000.10.4.337 [14] Kant, T., & Swaminathan, K. (2002). Analytical solutions for the static analysis of laminated composite and sandwich plates based on a higher-order refined theory. Composite Structures, 56(4), 329-344. https://doi.org/10.1016/S0263-8223(02)00017-X [15] Tian, A., Ye, R., & Chen, Y. (2016). A new higher-order analysis model for sandwich plates with a flexible core. Journal of Composite Materials, 50(7), 949-961. doi:10.1177/0021998315584650 [16] Thomsen, O.T., & Rits, W. (1998). Analysis and design of sandwich plates with inserts—a high-order sandwich plate theory approach. Composites Part B: Engineering, 29(6), 795-807. https://doi.org/10.1016/S1359-8368(98)00019-5. [17] Rahmani, O., Khalili, S.M.R., & Thomsen, O.T. (2012). A high-order theory for the analysis of circular cylindrical composite sandwich shells with a transversely compliant core. Composite Structures, 94(7), 2129-2142. https://doi.org/10.1016/j.compstruct.2012.02.002 [18] Piskunov, V.G., Verijenko, V.E., Adali, S., & Summers, E.B. (1993). A higher-order theory for the analysis of laminated plates and shells with shear and normal deformation. International Journal of Engineering Science, 31(6), 967-988. https://doi.org/10.1016/0020-7225(93)90106-5 [19] Nguyen, K.T., Thai, T.H., & Vo, T.P. (2015). A refined higher-order shear deformation theory for bending, vibration and buckling analysis of functionally graded sandwich plates. Steel and Composite Structures, 18(1), 91-120. DOI: https://doi.org/10.12989/scs.2015.18.1.091. [20] Dafedar, J.B., Desai, Y.M., & Mufti, A.A. (2003). Stability of sandwich plates by mixed, higher-order analytical formulation. International Journal of Solids and Structures, 40(17), 4501-4517. https://doi.org/10.1016/S0020-7683(03)00283-X. [21] Jedari Salami, S., Sadighi, M., & Shakeri, M. (2014). Improved extended high order analysis of sandwich beams with a bilinear core shear behavior. Journal of Sandwich Structures & Materials, 16(6), 633-668. doi:10.1177/1099636214548614 [22] Li, R., & Kardomateas, G. (2009). A high-order theory for cylindrical sandwich shells with flexible cores. Journal of Mechanics of Materials and Structures, 4(7-8), 1453–1467. doi:10.2140/jomms.2009.4.1453 [23] Brischetto, S., Carrera, E., & Demasi, L. (2009). Free Vibration of Sandwich Plates and Shells by Using Zig-Zag Function. Shock and Vibration, 16, Article ID 573674. Retrieved from https://doi.org/10.3233/SAV-2009-0483 [24] Brischetto, S., Carrera, E., & Demasi, L. (2009). Improved bending analysis of sandwich plates using a zig-zag function. Composite Structures, 89(3), 408-415. Retrieved from https://doi.org/10.1016/j.compstruct.2008.09.001 [25] Alipour, M. M., & Shariyat, M. (2015). Analytical zigzag formulation with 3D elasticity corrections for bending and stress analysis of circular/annular composite sandwich plates with auxetic cores. Composite Structures, 132, 175-197. Retrieved from https://doi.org/10.1016/j.compstruct.2015.05.003 [26] Pandit, M. K., Sheikh, A. H., & Singh, B. N. (2010). Analysis of Laminated Sandwich Plates Based on an Improved Higher Order Zigzag Theory. Journal of Sandwich Structures & Materials, 12(3), 307-326. doi:10.1177/1099636209104517 [27] Alipour, M. M., & Shariyat, M. (2012). An elasticity-equilibrium-based zigzag theory for axisymmetric bending and stress analysis of the functionally graded circular sandwich plates, using a Maclaurin-type series solution. European Journal of Mechanics - A/Solids, 34, 78-101. https://doi.org/10.1016/j.euromechsol.2011.12.004 [28] Maturi, D. A., Ferreira, A. J. M., Zenkour, A. M., & Mashat, D. S. (2014). Analysis of sandwich plates with a new layerwise formulation. Composites Part B: Engineering, 56, 484-489. Retrieved from https://doi.org/10.1016/j.compositesb.2013.08.086 [29] Pandey, S., & Pradyumna, S. (2015). A layerwise finite element formulation for free vibration analysis of functionally graded sandwich shells. Composite Structures, 133, 438-450. https://doi.org/10.1016/j.compstruct.2015.07.087 [30] Goswami, S., & Becker, W. (2016). Analysis of sandwich plates with compressible core using layerwise refined plate theory and interface stress continuity. Journal of Composite Materials, 50(2), 201-217. doi:10.1177/0021998315572929 [31] Tornabene, F., Brischetto, S. (2018). 3D capability of refined GDQ models for the bending analysis of composite and sandwich plates, spherical and doubly-curved shells. Thin-Walled Structures, 129, 94-124. doi:10.1016/j.tws.2018.03.021 [32] Xue, M., Cheng, L., Hu, N. (2003). The stress analysis of sandwich shells faced with composite sheets based on 3D FEM. Composite Structures, 60(1), 33-41. doi:10.1016/S0263-8223(02)00312-4 [33] Brischetto, S. (2017). Exact three-dimensional static analysis of single- and multi-layered plates and shells. Composites Part B: Engineering, 119, 230-252. doi:10.1016/j.compositesb.2017.03.010 [34] Burlayenko, V. N., Sadowski, T. (2009). Analysis of structural performance of sandwich plates with foam-filled aluminum hexagonal honeycomb core. Computational Materials Science, 45(3), 658-662. doi:10.1016/j.commatsci.2008.08.018 [35] Safarabadi, M., Haghighi-Yazdi, M., Sorkhi, M., Yousefi, A. (2021). Experimental and numerical study of buckling behavior of foam-filled honeycomb core sandwich panels considering viscoelastic effects. Journal of Sandwich Structures & Materials, 23(8), 3985-4015. doi:10.1177/1099636220975168 [36] ABAQUS User’s Manual (2022). ABAQUS, Learning Edition [37] Pagano NJ. Exact solutions for rectangular composite and sandwich plates. J Compos Mater 1970;4:20–34. [38] Kant T, Pendhari SS, Desai YM. A New Partial Finite Element Model for Statics of Sandwich Plates. Journal of Sandwich Structures & Materials. 2007;9(5):487-520. doi:10.1177/1099636207073465 [39] Ramtekkar, G.S., Desai, Y.M. and Shah, A.H. (2002). Mixed Finite Element Model for Thick Composite Laminated Plates, Mechanics of Advanced Material and Structures, 9: 133–156.

Copyright

Copyright © 2023 S M Shiyekar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.