Fast Incremental Updating Frequent Pattern Growth algorithm for Mining

Abstract

When a new incremental database is added to an existing database, certain existing frequent item sets may become infrequent item sets, and vice versa. This is one of the most difficult tasks in association rule mining. As a result, certain old association rules may become invalid, while others may become legitimate. It\'s possible that rules will arise. For incremental association rule mining, we devised a new, more efficient method. A new Incremental Updating Frequent Pattern growth algorithm (FIUFP-Growth) was developed using a Fast Incremental Updating Frequent Pattern growth algorithm (FIUFP-Growth), as well as a compact sub-tree appropriate for incremental mining of frequent patterns Item sets. This approach extracts previously mined frequent item sets and their support counts from the original database, then uses them to efficiently mine frequent item sets from the updated database minimizing the amount of original database rescans. Our algorithm was able to minimize when compared to individual FP-Growth, needless sub-tree creation consumes more resources and time. According to the results, our algorithm\'s average execution time for pattern growth mining is 46 percent faster than apriori and eclat algorithm. This method for mining incremental association rules and our findings could directly aid computer business intelligence designers and developers methods.

Introduction

I. INTRODUCTION

Association rule mining is a well-known and commonly used data mining technique  that has been used to extract patterns or links between sets of data in huge databases. It's been used in a variety of settings, including medicine, education, and business. In general, association rule mining entails the following steps: There are two important sub-tasks: first, often generated item sets, locating frequently occurring item sets that satisfy a minimum level of support threshold, and second, the development of association rules, both from the frequently derived item sets that satisfy a minimum confidence level A criterion in the form of A B. The majority of researchers have focuses on increasing the efficiency of regular itemset mining, which typically costs a lot of resources and time calculate the time.

Many scholars have developed methods for detecting frequent itemset over the last decade. The Apriori algorithm is a common algorithm for discovering frequent item sets: it creates many candidate item sets and requires multiple database searches, resulting in significant lost time resources as well as compute time.  The FP-Growth algorithm has been utilised to remedy this issue, however there is no candidate.The production of item sets reduces the amount of database scans.As a result, the FP-Growth method is more efficient than other algorithms.

A fast incremental updating frequent pattern growth algorithm (FIUFP-Growth), and devised a new approach for incremental association rule mining incremental conditional pattern tree.

It increased the speed with which frequently updated item sets were updated, by lowering the time it takes to generate conditional pattern trees or sub-trees.

For frequent itemset mining, the Eclat algorithm uses a vertical data format called item-TID, which means item: set of TIDs, where item refers to an item name and TID refers to a set of transaction numbers for transactions containing the item.

Existing frequent item sets and association rules may become invalid if new transaction data or an incremental database is added to the old database, necessitating the generation of new frequent item sets and association rules. To solve such a problem, the first step is to mine all frequent item sets and construct association rules from the whole updated database, which includes both the incremental and original databases. This method, however, is inefficient and consumes resources as well as compute time.

To increase the efficiency of incremental frequent itemset mining, we built a new form of sub-tree, incremental conditional pattern tree (ICP-tree), and developed a novel approach for incremental association rule mining, a fast incremental updating frequent pattern growth algorithm (FIUFP-Growth).

The main idea was to retrieve previously discovered frequent item sets from the original database and use them to mine all frequent item sets from the updated FPISC-tree: this reduced the number of scans of the conditional pattern bases in the original path that were unnecessary, and improved the efficiency of updating frequent item sets by reducing the construction of conditional pattern trees or sub-trees. It also reduced the size of the sub-trees by creating them only from the new path's conditional pattern bases.

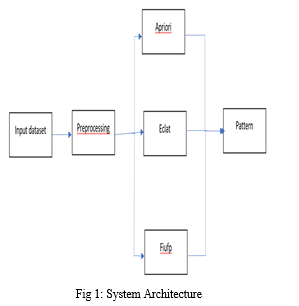
The II section consists of literature survey, III section consists of the proposed system and final IV section consists of the results and section V is about conclusion.

II. LITERATURE SURVEY

J. Sun, Y. Xun, J. Zhang, and J. Li [1] proposed a Frequent item sets mining (FIM) as well as other mining techniques has been being challenged by large scale and rapidly expanding datasets. To address this issue, we propose a solution for incremental frequent item sets mining using a Full Compression Frequent Pattern Tree (FCFP-Tree) and related algorithms called FCFPIM. Unlike FP-tree, the FCFP-Tree maintains complete information of all the frequent and infrequent items in the original dataset. This allows the FCFPIM algorithm not to waste any scan and computational overhead for the previously processed original dataset when new dataset are added and support changes. Therefore, much processing time is saved. Importantly, FCFPIM adopts an effective tree structure adjustment strategy when the support of some items changes due to the arrival of new data. FCFPIM is conducive to speeding up the performance of incremental FIM. Although the tree structure containing the lossless items information is space-consuming, a compression strategy is used to save space. We conducted experiments to evaluate our solution, and the experimental results show the space-consuming is worthwhile to win the gain of execution efficiency, especially when the support threshold is low.

Y. Djenouri, J. C.-W. Lin, K. Norvag, and H. Ramampiaro [2] proposed a Frequent item sets mining (FIM) as well as other mining techniques has been being challenged by large scale and rapidly expanding datasets. To address this issue, we propose a solution for incremental frequent item sets mining using a Full Compression Frequent Pattern Tree (FCFP-Tree) and related algorithms called FCFPIM. Unlike FP-tree, the FCFP-Tree maintains complete information of all the frequent and infrequent items in the original dataset. This allows the FCFPIM algorithm not to waste any scan and computational overhead for the previously processed original dataset when new dataset are added and support changes. Therefore, much processing time is saved. Importantly, FCFPIM adopts an effective tree structure adjustment strategy when the support of some items changes due to the arrival of new data. FCFPIM is conducive to speeding up the performance of incremental FIM. Although the tree structure containing the lossless items information is space-consuming, a compression strategy is used to save space. We conducted experiments to evaluate our solution, and the experimental results show the space-consuming is worthwhile to win the gain of execution efficiency, especially when the support threshold is low.

W. Kreesuradej and W. Thurachon [3] proposed method to In this paper, we propose a new FP-Growth algorithm for incremental association rule discovery. We also design a new FPISC-tree based on the FUFP-tree structure. The new FPISC-tree is more suitable for the task of incremental association rule discovery than FUFP-tree structure. The basic ideas of the proposed algorithm are to retrieve the frequent item sets from the original database and to use their support count in the update of the new support count of the incremental database so that the original paths do not need to be reprocessed as well as to strategically use them to discover frequent item sets from the FPISC-tree. Experimental results show that the proposed algorithm was able to reduce the number of constructed subtrees and the execution time was significantly less than those of the FPGrowth and FUFP-tree.

A. Ariya and W. Kreesuradej [4] proposed In the real world of data, a new set of data has been being inserted into the existing database. Thus, the rule maintenance of association rule discovery in large databases is an important problem. Every time the new data set is appended to an original database, the old rule may probably be valid or invalid. This paper proposed the approach to calculate the lower minimum support for collecting the expected frequent item sets. The concept idea is applying the normal approximation to the binomial theory. This proposed idea can reduce a process of calculating probability value for all item sets that are unnecessary. In addition, the confidence interval is also applied to ensure that the collection of expected frequent item sets is properly kept.

Y. Djenouri, A. Belhadi, P. Fournier-Viger, and H. Fujita [5] proposed Association Rule Mining (ARM) is a fundamental data mining task that is time-consuming on big datasets. Thus, developing new scalable algorithms for this problem is desirable. Recently, Bee Swarm Optimization (BSO)-based meta-heuristics were shown effective to reduce the time required for ARM. But these approaches were applied only on small or medium scale databases. To perform ARM on big databases, a promising approach is to design parallel algorithms using the massively parallel threads of a GPU processor.

While some GPU-based ARM algorithms have been developed, they only benefit from GPU parallelism during the evaluation step of solutions obtained by the BSO-metaheuristics. This paper improves this approach by parallelizing the other steps of the BSO process (diversification and intensification). Based on these novel ideas, three novel algorithms are presented, i) DRGPU (Determination of Regions on GPU), ii) SAGPU (Search Area on GPU, and, iii) ALLGPU (All steps on GPU). These solutions are analyzed and empirically compared on benchmark datasets. Experimental results show that ALL GPU outperforms the three other approaches in terms of speed up. Moreover, results confirm that ALLGPU outperforms the state-of-the-art GPU-based ARM approaches on big ARM databases such as the Webdocs dataset. Furthermore, ALL GPU is extended to mine big frequent graphs and results demonstrate its superiority over the state-of-the-art D-Mine algorithm for frequent graph mining on the large Pokec social network dataset.

III. PROPOSED SYSTEM

They presented an effective way for discovering important associations between goods in retail transactions using association rule mining. Apriori algorithm, a well-accepted and easy approach for identifying frequent item sets and association rules, was proposed a year later. This method developed and tested potential itemets on a level-by-level basis to see if they were frequent or infrequent. The production of many candidate item sets, which required multiple database scans, a lot of storage space, and a lot of compute time, was a restriction to this notion.

developed a novel strategy for efficiently mining frequent item sets from an updated FPISC-tree, our Fast Incremental Updating Frequent Pattern Growth Algorithm (FIUFP Growth). This solution introduces a new incremental conditional pattern tree (ICP tree) to store and represent frequent item sets, as well as their support counts, in updated and incremental databases, allowing for more efficient processing of incremental frequent item sets when new transactions are introduced. FIUFP-Growth not only enhances the FP-tree structure but also the mining process of frequent item sets from the updated FP-tree while solving an incremental association mining problem.

Algorithm

Step 1: FIUFP-Growth algorithm starts to mine frequent item sets associated with item ‘e’.

Step 2: Item ‘e’ is not a new frequent item or newFrequentItem, then go to Step 3-11.

Step 3: The algorithm generates a conditional pattern base for the incremental database (condNewPath) and the original database (condOrgPath). Three paths ending with node ‘e’ are found in condNewPath including [‘b’,‘a’,‘c’,‘d’]:3, ‘b’,‘c’,‘d’]:1, and [‘a’,‘d’]:1, and two paths in the condOrgPath including [‘b’,‘a’,‘d’]:2, and [‘b’,‘a’]:.

Step 4: The algorithm counts each item only from the condNewPath and then put them into either the frequentList or infrequentList by comparing the support count for each item with the support threshold of the incremental database which is 2; hence, the frequentList is now{’a’:4,’b’:4,‘d’:5,’c’:4} and the infrequentList is{}.

Step 5: The algorithm starts to categorize the frequentList and infrequentList, that is{’a’:4,’b’:4,‘d’:5,’c’:4} and{}, into four cases.

Step 6: For case#1, the algorithm generates patterns by concatenating each item in the freqeuntList with the root-item ‘e’. In this case, item ‘a’:4 is processed first, then a pattern (‘ae’) is generated, followed by pattern (‘be’), ‘ce’), and ‘de’).

Step 7: Pattern ‘ae’):4, and ‘be’):4 are available in the set of frequent item sets in the original database as shown in Table 4, sogo to sub-step 7-1. Unlike patterns (‘ae’) and ‘be’), both (‘de’):5 and ‘ce’):4 are not available in the set of frequent item sets in the original database.

Hence, do sub-step 7-2, i.e., put them into a set of rescan_original for mining frequent item sets in the step 9 (case#3).

sub-step 7-1: The updated support count for pattern (‘ae’) is thus 3+ = 7, and the count for pattern ‘be’) is 3 + 4 = 7. The counts of both patterns are also greater than the updated support threshold, hence they become frequent patterns. The algorithm collects (‘ae’):7, and (‘be’):7 into the newFIS.

sub-step 7-2: rescan_original = {(‘d’):5, (‘c’):}.

Step 8: For case#2, the algorithm considers each item in the frequentList set, but there are no items in frequentList, hence there are no items that satisfy the condition for this case.

Step 9: For case#3, the algorithm considers each item in the rescanOriginal set, that is, {(‘d’):5, (‘c’):}.Item‘’ is considered first. In order to update the support count of patterns‘de’, its original support count must be obtained by rescanning and counting item in the condOrgPath ([‘b’,‘a’,‘d’]:2, and [‘b’,‘a’]:1.).

The support count of item ‘d’ turns out to be 2. Hence, the updated support count for item ‘d’ is 2 + 5 = 7, which is also greater than the updated support threshold.

Step 10: The algorithm generates pattern (de).

sub-step 10-1: Appends (‘de’):5 to the newFIS. Item d is inserted into fList{‘a’:4, ‘b’:4, ‘d’:}. On the other hand, the updated support count for item ‘c’, 0 + 4 = 4, which is less than 5; hence, the algorithm ignores this item.

Step 11: Then, the set of new 2-item-long frequent item sets associated with item ‘e’ is {(‘ae’): 7, (‘be’): 7,(‘de’): 7}, and the sorted fList with frequent items and their support count in the incremental database is{‘d’:5, ‘a’:4, ‘b’:4}. The number of all items in fList is greater than 1; hence, the process for mining 3-item-long frequent pattern associated with item ‘e’ is performed.

Step 12: The algorithm constructs an incremental conditional pattern tree, or ICP-tree from only the incremental database, or conditional pattern based from the incremental database (condNewPath): [‘b’,‘a’,‘c’,‘d’]:3, [‘b’,‘c’,‘d’]:1, and [‘a’,‘d’]:1, by utilizing the frequent items in the sorted fList:{‘d’:5, ‘a’:4, ‘b’:} as shown in Fig. 8 (a) to 8 (c).

Step 13: Next, the algorithm continues to discover frequent item sets starting from item ‘b 0 from the bottom of the sub_headertable: {‘b’:4, ‘a’:4, ‘d’:5} by recursively calling the incremental pattern growth algorithm in step 3-12 until the number of all items in fList is less than or equal to.

Step 14: Finally, when the iteration process of mining frequent pattern ending with item ‘e’ is completed, all frequent item sets associated with item ‘e’ are as follows: (‘e’):8, (‘ae’):7, (‘be’):7, (‘de’):7, (‘ab’):6, (‘db’):6, (‘dabe’):5, and (‘da’):6. The example, presented above, is an example of only (k = 2) item frequent item sets mining, associated with item ‘e’

A. Apriori algorithm

The apriori algorithm is a method of extracting frequent product sets and relevant association rules. In most cases, the apriori technique is used on a database with a large number of transactions. Customers, for example, can purchase products at a Big Bazar.

The Apriori algorithm makes it easier for shoppers to acquire their products and improves the store's sales success.

B. Eclat algorithm

Equivalence class clustering and bottom up lattice transversal algorithm are abbreviated as Eclat Algorithm. It's a method for locating frequently occurring item sets in a transaction or database. It is one of the most effective approaches for learning Association Rules. In a database, the Eclat algorithm is used to build frequent item sets.

For finding common item sets, the Eclat algorithm uses a depth first search, whereas the Apriori algorithm uses a breadth first search. It represents data in a vertical pattern, as opposed to the horizontal pattern used by the Apriori method. The Eclat method is faster than the Apriori algorithm because of its vertical layout. As a result, the Eclat algorithm is a faster and more scalable variant of the Association Rule Learning method.

Conclusion

With our fast incremental updating frequent pattern growth algorithm (FIUFP), we increased the efficiency of incremental frequent pattern mining and built a new incremental frequent pattern mining technique . ICP-tree is a conditional pattern tree that can be used for incremental learning. mining of often occurring item sets The main concept was to make use of often occurring item sets, which have previously been extracted from the original to support the rapid updates to the database and associated support counts mining of itemset.

References

[1] J. Sun, Y. Xun, J. Zhang, and J. Li, ‘‘Incremental frequent item sets mining with FCFP tree,’’ IEEE Access, vol. 7, pp. 136511–136524, 2019. [2] Y. Djenouri, J. C.-W. Lin, K. Norvag, and H. Ramampiaro, ‘‘Highly efficient pattern mining based on transaction decomposition,’’ in Proc. IEEE 35th Int. Conf. Data Eng. (ICDE), Macao, China, Apr. 2019, pp. 1646–1649. [3] W. Kreesuradej and W. Thurachon, ‘‘Discovery of incremental association rules based on a new FP-growth algorithm,’’ in Proc. IEEE 4th Int. Conf. Comput. Commun. Syst. (ICCCS), Singapore, Feb. 2019, pp. 184–188. [4] A. Ariya and W. Kreesuradej, ‘‘An enhanced incremental association rule discovery with a lower minimum support,’’ Artif. Life Robot., vol. 21, no. 4, pp. 466–477, Dec. 2016. [5] Y. Djenouri, A. Belhadi, P. Fournier-Viger, and H. Fujita, ‘‘Mining diversified association rules in big datasets: A cluster/GPU/genetic approach,’’ Inf. Sci., vol. 459, pp. 117–134, Aug. 2018.

Copyright

Copyright © 2023 Archana Madhusudhanan, Shameem S. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.