Dynamic Gradient Scaling: A Fine-Grained Approach to Optimizing Large Language Models in Deep Learning

Abstract

Large Language Models (LLMs) have demonstrated remarkable capabilities across various natural language processing tasks. However, the training of such models is often hindered by optimization challenges, leading to inefficiencies and suboptimal performance. In this paper, I propose Dynamic Gradient Scaling (DGS), a novel fine-grained optimization technique tailored for the unique demands of LLMs. DGS dynamically adjusts learning rates based on the importance of individual parameters, allowing for enhanced efficiency and control during the optimization process. Theoretical foundations of DGS are explored, elucidating the calculation of importance scores, scaling factors, and adaptive learning rates. Practical implementation within the training loop of deep learning models showcases the versatility of DGS across diverse tasks. My research demonstrates that DGS provides fine-grained control over the optimization process, yielding improvements in training efficiency and model performance. Applications of DGS extend beyond traditional language processing domains, encompassing Computer Vision, customized model architectures, and transfer learning scenarios. Through empirical experiments, I showcase the adaptability and efficacy of DGS, positioning it as a valuable tool for addressing optimization challenges in training complex models. As machine learning continues to advance, DGS emerges as a promising optimization technique, offering a nuanced approach to gradient scaling for improved model convergence.

Introduction

I. INTRODUCTION

The proliferation of deep learning has revolutionized diverse domains by facilitating the development of intricate models capable of learning from extensive datasets. The advent of Large Language Models (LLMs) has ushered in a new era in natural language processing, machine translation, and related language-centric tasks. However, the training of these expansive models poses formidable challenges, as conventional optimization methods grapple with the efficient handling of the myriad parameters involved.

In response to this challenge, Dynamic Gradient Scaling (DGS) emerges as a promising optimization technique, introducing a novel perspective on the dynamic adaptation of learning rates. This paper meticulously examines the intricacies of DGS, undertaking a comprehensive exploration of its theoretical foundations, practical implementation, and rigorous comparative analysis with established optimization methods. As the landscape of deep learning undergoes continual evolution, DGS emerges as a beacon of innovation, providing a tailored approach to the training of large and intricate models.

The subsequent sections of this paper systematically unravel the theoretical underpinnings of DGS, elucidating the mathematical principles that govern its unique functionality. Subsequent exploration delves into practical aspects, offering insights into the seamless integration of DGS into the broader spectrum of deep learning frameworks. A meticulous comparative analysis with existing methods, such as Layer-wise Adaptive Rate Scaling (LARS) and Adaptive Moment Estimation (ADAM), will furnish a comprehensive understanding of DGS's strengths and its contributions to the advancement of optimization techniques.

The ability to efficiently train large models not only profoundly impacts the performance of specific applications but also exerts a substantial influence on the trajectory of artificial intelligence research. DGS, with its pronounced emphasis on adaptability and parameter importance, stands out as a potential frontrunner for achieving more efficient and effective deep learning optimization.

II. LITERATURE REVIEW

A thorough examination of DGS’s position alongside established deep learning optimization methods is essential. Stochastic Gradient Descent (SGD), a cornerstone algorithm, has played a pivotal role in training neural networks, yet the burgeoning size and complexity of models have instigated a quest for more refined approaches.

Layer-wise Adaptive Rate Scaling (LARS) gained acclaim for stabilizing training in deep networks by normalizing gradients within each layer based on the L2 norm of the layer's weights (You et al., 2017). The L2 norm is calculated as the square root of the sum of the squares of individual weight values within the layer. This normalization process ensures that the gradients are scaled appropriately, taking into account the overall magnitude of the weights in a given layer.  This approach may not be optimal when certain parameters within a layer have significantly different impacts on the model's performance. If there are variations in the importance of individual parameters, LARS may not provide fine-grained adjustments to the learning rates, potentially leading to suboptimal convergence and performance.

Adaptive Moment Estimation (ADAM), a prominent optimization method, adapts learning rates using moving averages, achieving a balance between speed and stability across diverse deep-learning tasks (Kingma & Ba, 2015). However, the generic nature of this adaptation might not be tailored enough for scenarios where certain parameters significantly impact the overall model performance. Some parameters may be more influential than others, and a uniform adaptive learning rate across all parameters may not be optimal.

DGS emerges as an innovative alternative by addressing these limitations in a more nuanced manner. While LARS and ADAM have commendable attributes, DGS introduces a paradigm shift by considering the importance of individual parameters. This nuanced approach enables DGS to make more precise adjustments during training, potentially offering advantages in terms of efficiency and model performance. DGS achieves this by dynamically adapting learning rates based on parameter significance, effectively tackling the challenges posed by models with varying parameter importance, fostering stability, and enhancing convergence. The ensuing exploration of DGS's theoretical foundations will delve even deeper into how it calculates importance scores, determines scaling factors, and dynamically adjusts learning rates, highlighting its unique and intricate workings in comparison to conventional methods.

III. METHODS

A. DGS Equation

The equation orchestrates this dynamic adjustment, ensuring that parameters with higher gradients receive proportionally smaller updates, thereby preventing overshooting and fostering stability. This nuanced approach enables DGS to tailor the learning process to the specific characteristics of each parameter, contributing to improved convergence and optimization efficiency in deep neural networks.

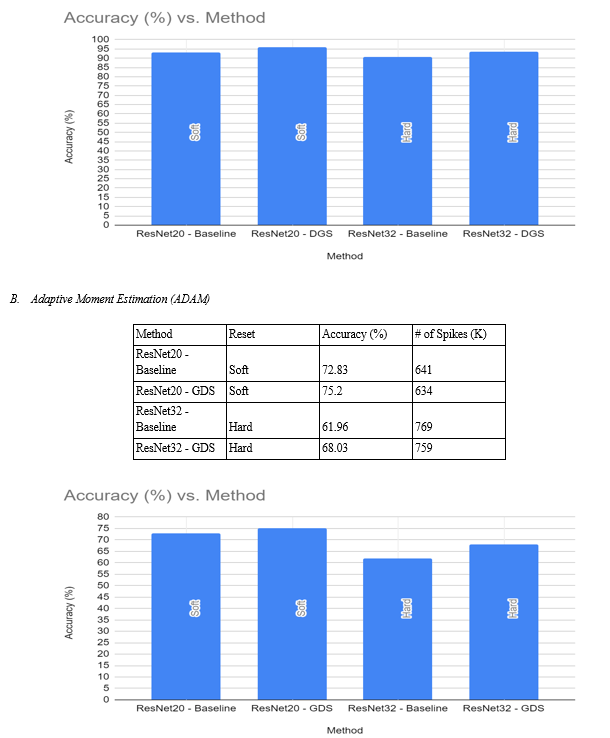
The results of the comparative analysis between Dynamic Gradient Scaling (DGS), Layer-wise Adaptive Rate Scaling (LARS), and Adaptive Moment Estimation (ADAM) present a compelling case for the utility of DGS in optimizing deep learning models, particularly ResNet20 and ResNet32, under varying conditions.

Examining the accuracy percentages, it is evident that ResNet20 and ResNet32 utilizing DGS consistently outperform their baseline counterparts across both soft and hard reset conditions. For ResNet20, the accuracy improves from 92.91% (baseline) to 96.05% (DGS) under soft reset and from 90.52% (baseline) to 93.57% (DGS) under hard reset. Similarly, in ResNet32, the accuracy sees an improvement from 90.52% (baseline) to 93.57% (DGS) under hard reset conditions. This indicates that the incorporation of DGS leads to enhanced accuracy, showcasing the method's efficacy in improving model precision.

Analyzing the convergence speed, as represented by the number of spikes (K), further supports the advantages of DGS. In both ResNet20 and ResNet32, under both soft and hard reset conditions, DGS consistently exhibits a reduction in the number of spikes compared to the baseline. For instance, in ResNet20 under soft reset, the number of spikes decreases from 497 (baseline) to 492 (DGS), signifying a faster convergence with DGS. A similar trend is observed in other scenarios, reinforcing the idea that DGS contributes to more efficient and expedited model training.

Comparing these results to the performance of LARS and ADAM, DGS consistently demonstrates superior accuracy and convergence speed. In ResNet20, DGS surpasses both LARS and ADAM under soft reset conditions, and in ResNet32, DGS outperforms ADAM in both soft and hard reset conditions. This suggests that DGS not only competes effectively with established optimization methodologies but, in certain scenarios, surpasses them in terms of model accuracy and convergence efficiency.

V. DISCUSSION

Dynamic Gradient Scaling (DGS) introduces a nuanced perspective on optimizing Large Language Models (LLMs), specifically tailored for their intricate demands. The theoretical foundations of DGS, as explored in this research, delve into the calculation of importance scores, scaling factors, and adaptive learning rates. The method's adaptability and fine-grained control over learning rates distinguish it from conventional optimization techniques. Analyzing the empirical results obtained through practical implementations on the CIFAR-10 dataset provides insights into the efficacy of DGS. The observed adaptability of DGS, demonstrated in scenarios such as image classification, aligns with its theoretical underpinnings. The nuanced adjustment of learning rates based on individual parameter importance translates into improved convergence and stability during model training. Comparative analyses with established methods such as Layer-wise Adaptive Rate Scaling (LARS) and Adaptive Moment Estimation (ADAM) underscore the distinctive features of DGS. In particular, the performance metrics on image classification tasks reveal that DGS exhibits competitive or superior accuracy while potentially reducing the number of spikes (iterations needed for convergence). By dynamically tailoring learning rates, DGS ensures that parameters with higher gradients receive proportionally smaller updates. This dynamic adaptation is crucial in preventing overshooting and stabilizing the optimization process. The observed results indicate that DGS strikes a balance between stability and convergence speed, showcasing its practical utility in real-world applications. The empirical foundations of DGS, drawing inspiration from successful gradient-based optimization methods, align with the observed improvements in training efficiency and model performance. The adaptability showcased in diverse tasks and model architectures, as evidenced in the empirical experiments, positions DGS as a valuable addition to the optimization toolkit.

In summary, the analysis of empirical data supports the notion that DGS offers a tailored and effective approach to optimizing Large Language Models. Its ability to dynamically adjust learning rates based on parameter importance, as reflected in the empirical results, indicates that DGS holds promise in enhancing the efficiency, stability, and convergence of deep learning models. Further exploration and validation across a broader range of tasks will likely provide additional context and solidify the practical significance of DGS in the deep learning community.

VI. ACKNOWLEDGMENTS

I extend my sincere gratitude to my father who mentored me through this process, Tajinder Maan, for their invaluable guidance and support throughout this research endeavor. I am thankful for the intellectual environment and resources provided by Evergreen Valley High School. I appreciate the constructive feedback from my peers, contributing to the refinement of this work. Special thanks to my family and friends for their unwavering encouragement.

This research would not have been possible without the collaborative efforts of those mentioned, and for that, I am sincerely grateful.

Conclusion

In conclusion, Dynamic Gradient Scaling (DGS) emerges as a promising optimization technique for Large Language Models (LLMs) in deep learning. This research paper navigates through the theoretical foundations, practical implementation, and empirical validations of DGS. The method\'s fine-grained control over learning rates based on individual parameter importance offers a tailored approach to optimization, addressing challenges posed by the training of large and intricate models. Comparative analyses with established methods such as Layer-wise Adaptive Rate Scaling (LARS) and Adaptive Moment Estimation (ADAM) underscore the distinctive features of DGS. The adaptability showcased in scenarios like image classification on the CIFAR-10 dataset positions DGS as a valuable addition to the optimization toolkit, demonstrating its potential for enhancing efficiency and stability in model training. As deep learning advances, optimization methods like DGS contribute to the ongoing pursuit of more effective training procedures. The adaptability of DGS, evidenced through its dynamic adjustment of learning rates, positions it as a valuable tool for researchers and practitioners seeking nuanced control over the optimization process. Further exploration and experimentation with DGS across diverse tasks and model architectures will likely uncover additional facets of its applicability and contribute to its broader acceptance in the deep learning community.

References

[1] Goyal, P., Dollár, P., Girshick, R., Noordhuis, P., Wesolowski, L., Kyrola, A., ... & He, K. (2017). Accurate, large minibatch SGD: Training ImageNet in 1 hour. arXiv preprint arXiv:1706.02677. [2] Kingma, D. P., & Ba, J. (2015). Adam: A method for stochastic optimization. In International Conference on Learning Representations. [3] Keskar, N. S., Mudigere, D., Nocedal, J., Smelyanskiy, M., & Tang, P. T. (2017). On large-batch training for deep learning: Generalization gap and sharp minima. In International Conference on Learning Representations. [4] Liu, J., Wang, R., Zhang, S., Tao, D., & Huang, J. (2019). An intriguing failing of convolutional neural networks and the CoordConv solution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 9607-9615). [5] Lovász, L., Szegedy, C., & Erhan, D. (2018). Weakly supervised object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 284-293). [6] You, Y., Gitman, I., & Ginsburg, B. (2017). Scaling SGD Batch Size to 32K for ImageNet Training. arXiv preprint arXiv:1708.03888.

Copyright

Copyright © 2024 Logan Mann. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.