The Design of FIR Filter Based on improved DA Algorithm and its FPGA implementation: REVIEW

Abstract

This research investigates challenges in employing the Distributed Arithmetic (DA) algorithm for Finite Impulse Response (FIR) filters on Field-Programmable Gate Arrays (FPGAs). Focusing on coefficient representation, it explores precision trade-offs via fixed-point arithmetic and quantization. Memory optimization strategies, such as efficient storage within FPGA resources, are analysed to reduce memory requirements. Enhancing computational speed involves optimizing lookup table access and architectural modifications. Efficient management of FPGA resources and trade-offs between latency, throughput, and resource usage are also explored. Algorithmic refinements specific to DA-based FIR filters are studied to enhance resource utilization and computational efficiency. Overall, this work offers insights and solutions spanning algorithm design, memory utilization, lookup table speed, and FPGA architecture for more efficient DA-based FIR filter implementations on FPGAs.

Introduction

I. INTRODUCTION

Digital signal processing relies on filters like Finite Impulse Response (FIR) filters for crucial tasks. FIR filters demand efficient design methodologies, and an emerging approach involves utilizing an Improved Differential Evolution Algorithm (DA) to optimize filter coefficients.

This amalgamation aims to enhance filter performance, reducing passband ripples and stopband distortions. The endeavour involves simulating the improved DA algorithm in MATLAB or Python, optimizing filter coefficients to meet specific criteria. Subsequently, FPGA implementation becomes pivotal, requiring hardware description languages (HDL) to describe the filter architecture. Testing, validation, and iterative refinement ensure the filter meets stringent specifications. The process encompasses DSP principles, optimization techniques, and FPGA design proficiency for a high-performance FIR filter implementation

This synergy between DSP and evolutionary algorithms entails simulating the refined DA algorithm using computational tools like MATLAB or Python. The algorithm's output, optimized filter coefficients, is crucial in the subsequent stage of FPGA (Field

A. Programmable Gate Array) Implementation

FPGA implementation necessitates translating the optimized filter coefficients into hardware description languages (HDL) such as Verilog or VHDL. This step facilitates the creation of a hardware architecture that realizes the FIR filter's functionality on the FPGA platform.

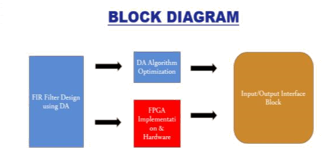
1. FIR Filter Design using DA: This block represents the design process of the FIR filter utilizing the Differential Evolution algorithm.
2. DA Algorithm Optimization: Dedicated to the optimization stages performed by the Differential Evolution algorithm to refine the filter's coefficients.
3. FPGA Implementation & Hardware: Encompassing the implementation of the designed FIR filter onto the FPGA hardware. This block also includes configurations and connections necessary for execution.
4. Input/Output Interface Block: Represents the interfaces for inputting data into the filter and retrieving the processed output signals.

II. RELATED WORKS

1. Gaowei Xu, Yao Zou, Jun Han, Xiaoyang Zeng, "Low power design for FIR filter", 2013 IEEE 10th International Conference on ASIC, pp.1-4, 2013.

We compare three low-power schemes for the multithreaded pipeline design of FIR digital filters. We use an optimal CCSD encoding method to minimize the number additive/subtractors in our design. Additionally, we use the 16-bit 16 taps low pass FIR filter to compare the performance of these three algorithms. Finally, we synthesize the designs in SMIC65nm library to evaluate their performance. The results show that the optimal CCSD scheme performs better than the two other low-power schemes with the same throughput.

2. Baozhong Xie, Chen Tiequn, "Improved distributed algorithm via Zero-Padding and Multi-Port ROM structure", IEEE 2011

10th International Conference on Electronic Measurement & Instruments, vol.1, pp.172-175, 2011

vector inner product operation is one of the most common methods of signal processing, particularly in digital filter. Calculating speed and occupied resources have a significant impact on signal processing systems.

A traditional Serial Shift-Summation Distribution algorithm (DA) requires a lot of shifting operations but not very high calculating speed. Complete pipeline parallel structure requires a lot of chip resources of FPGA.

For these reasons, we presented an improved method.

We synthesized the distributed algorithm using multi-port read only memory ( MPROM) using a look-Up table in FPGAs.

In logic shift operation, we replaced it with zero-padding to reduce the resource occupation and calculate time delay.

Verification by simulation and synthesis showed that this improved algorithm can achieve the performance of full pipeline parallel structure, but only requires the resource occupation of serial shift-Summation structure.

3. Cheng - Hwang, D.W. Lin, "A family of low-complexity blind equalizers", IEEE Transactions on Communications, vol.52, no.3, pp.395-405, 2004.

The complexity and training of equalizers are two of the most important topics of equalizer design.

We present the blind equalizer family, which, by using the decomposition finite impulse response filter technique, can reduce the complexity of its convolution operation by approximately one half.

The prototype algorithm of this equalizer family uses the common Godard cost function. Some simplified algorithms are proposed, such as the sign algorithm, which avoids multiplications in coefficient adaptation, and several delayed versions.

In addition, we study the convergence properties of these algorithms. For the prototype algorithm, we demonstrate that, at the limit of an infinitely large equalizer and under mild conditions on the signal constellation and channel characteristics of the performance surface, there are only two local minima.

One of the local minima is undesirable and has a null equalized channel response, while the other corresponds to perfect equalisation, which can be achieved by proper equalizer initialization.

Some understanding of their convergence behaviours is obtained by examining their adaptation equations, and simulation results are presented.

4. Din-Yuen Chan, Jar-Ferr Yang, Chun-Chin Fang, "Fast implementation of MPEG audio coder using a recursive formula with fast discrete cosine transform", IEEE Transactions on Speech and Audio Processing, vol.4, no.2, pp.144-148, 1996.

In the case of cosine modulation multirate sub band filtering, we suggest two implementation algorithms to decrease the computational complexity.

First, we develop a recurrence-based algorithm to further reduce the computational complexity of polyphase sub band filtering as proposed by the Nussbaumer-Vetterli (1984) algorithm.

Since the cosine modulation is implemented by discrete cosine transform, we combine the fast decimation in time (DIT) DCT method with the decimation in frequency (DIF) method to further reduce the calculation.

For example, the recurrence formula with mixed fast method requires approximately 13.2% for the multiplications and about 41.6% for the additions as recommended by ISO Std.

5. In the paper [5] L. Zhao, W. H. Bi, and F. Liu, "Design of digital FIR bandpass filter using a distributed algorithm based on FPGA", Electronic Measurement Technology, vol. 30, pp. 101-104, 2007.

In aerospace applications, accelerometers are implemented with FIR filter by DA algorithm. Direct application of DA algorithm to FPGA for realization of FIR filter is very difficult to achieve best configuration in FIR filter coefficient in terms of storage resource and computing speed. We proposed improved DA algorithm to overcome the above difficulties. DA algorithm uses split LUTS, which uses small memory usage and increases the operational speed. The specifications for decimation FIR filters will be based on the specifications of 3rd-order single Sigma-Delta modulator. Higher order decimation filter is suggested i.e., 48th order implementation with low hard ware complexity, the hardware model of the filter was verified using Verilog HDL.

6. H. Chen, C. H. Xiong, and S. N. Zhong, "FPGA-based efficient programmable polyphase FIR filter", Journal of Beijing Institute of Technology, vol. 14, pp. 4-8, 2005.

Modelling, Design and Implementation of High-Speed Programmable Polyphase Firing impulse Response (FIR) Filter with Field Programmable Gate Array (FPGA Technology)

High-speed Programmable Poly phased Firing impulse response (HFPFR) filter can be programmed to run automatically based on the programmed configuration word including Symmetry/Asymmetry, Odd/Even Tapping from 32 Tapping to 256 Tapping.

High-Speed Poly phased Filter with 12 Bit Signal and 12 Bit Coefficient Word-length is realized on Xilinx Virtex1500 device with maximum sampling frequency (160 MHz).

7. Y. T. Xu, C. G. Wang, and J. L. Wang, "Hardware Implementation of FIR Filter Based on DA Algorithm", Journal of PLA University of Science and Technology, vol. 4, pp. 22-25, 2003.

In aerospace applications, accelerometers are implemented with FIR filter by DA algorithm. Direct application of DA algorithm to FPGA for realization of FIR filter is very difficult to achieve best configuration in FIR filter coefficient in terms of storage resource and computing speed. We proposed improved DA algorithm to overcome the above difficulties. DA algorithm uses split LUTS, which uses small memory usage and increases the operational speed. The specifications for decimation FIR filters will be based on the specifications of 3rd-order single Sigma-Delta modulator. Higher order decimation filter is suggested i.e., 48th order implementation with low hard ware complexity, the hardware model of the filter was verified using Verilog HDL.

III. PROPOSED WORK

1. Optimized Integration with FIR Filter Design: Detail the specific ways in which this improved DA algorithm can be seamlessly integrated into FIR filter design. Explain how it complements the filtering process, optimizing coefficients, reducing computational load, or improving precision.
2. Expected Performance Gains: High light the anticipated performance enhancements resulting from the application of the improved DA algorithm in FIR filter design. Discuss how these improvements might manifest in terms of speed, accuracy, frequency response, or resource utilization compared to conventional FIR designs.
3. FPGA Implementation Strategie: Provide an in-depth overview of the methodologies and strategies intended for implementing the FIR filter on FPGA using the improved DA algorithm. Discuss hardware optimizations mapping algorithmic

Improvements to FPGA architecture, and resource utilization considerations for efficient real-time processing.

4. Comprehensive Performance Evaluation Metrics: Outline a comprehensive set of performance evaluation metrics and criteria to assess the designed FIR filter's performance on FPGA. These metrics might include throughput, latency, signal-to-noise ratio, power consumption, area utilization, and scalability concerning filter order.

5. Comparative Analysis with Existing Methods: Conduct a detailed comparative analysis to showcase how the proposed work using the improved DA algorithm stands out from or advances beyond existing FIR filter design methods. Highlight specific advantages, such as improved efficiency, reduced hardware requirements, or better performance metrics compared to alternative approaches.

6. Exploration of Real-World Applications: Discuss potential applications or domains where the enhanced FIR filter design, incorporating the improved DA algorithm and FPGA implementation, could            find practical utility. Highlight scenarios in communications, medical signal processing, radar systems, or other relevant fields where these advancements could offer tangible benefits.

IV. FUTURE SCOPE

1. Algorithm Refinement and Optimization: Continuous refinement of the Distributed Arithmetic (DA) algorithm to enhance its efficiency, precision, and adaptability to different FIR filter architectures. Exploring novel methods to optimize the algorithm further for specific applications or hardware configurations, aiming for even more efficient resource utilization.
2. Hardware Advancements and FPGA Optimization: Leveraging advancements in FPGA technology to better exploit the capabilities of the hardware, thereby improving the performance and efficiency of the FIR filter design. Exploring new FPGA architectures or emerging technologies that can better accommodate and leverage the improved DA algorithm for FIR filter implementation.
3. Real-Time Implementation and Deployment: Focusing on real-time implementations of FIR filters using the enhanced DA algorithm, targeting applications where low latency and high throughput are critical, such as in communication systems or signal processing.
4. Adaptation for Specific Applications: Tailoring the improved FIR filter design for specialized applications like biomedical signal processing, audio processing, adaptive filtering, or specific communication protocols, thereby customizing the design for niche requirements.
5. Machine Learning Integration: Investigating the integration of machine learning techniques or adaptive algorithms alongside the improved DA-based FIR filters to enable self-optimization and adaptability to changing signal characteristics.
6. Energy Efficiency and Low-Power Implementations: Exploring methodologies to optimize the FIR filter design using the improved DA algorithm for low-power and energy- efficient implementations, crucial for portable devices and IoT applications.
7. Standardization and Industry Adoption: Contributing towards standardization efforts to incorporate the optimized FIR filter design methodologies using improved DA algorithms into industry standards, fostering wider adoption and compatibility.

References

[1] Guowei Xu, Yao Zou, Jun Han, Xiaoyang Zeng, \"Low power design for FIR filter\", 2013 IEEE 10th International Conference on ASIC, pp.1-4, 2013. [2] Cheng-I Hwang, D.W. Lin, \"A family of low-complexity blind equalizers\", IEEE Transactions on Communications, vol.52, no.3, pp.395-405, 2004. [3] Cheng - Hwang, D.W. Lin, \"A family of low-complexity blind equalizers\", IEEE Transactions on Communications, vol.52, no.3, pp.395-405, 2004 [4] Din-Yuen Chan, Jar-Ferr Yang, Chun-Chin Fang, \"Fast implementation of MPEG audio coder using a recursive formula with fast discrete cosine transform\", IEEE Transactions on Speech and Audio Processing, vol.4, no.2, pp.144-148, 1996. [5] L. Zhao, W. H. Bi, and F. Liu, \"Design of digital FIR bandpass filter using a distributed algorithm based on FPGA\", Electronic Measurement Technology, vol. 30, pp. 101-104, 2007. [6] H. Chen, C. H. Xiong, and S. N. Zhong,\"FPGA-basedefficient programmable polyphase FIR filter\", Journal of Beijing Institute of Technology, vol. 14, pp. 4-8, 2005. [7] Y. T. Xu, C. G. Wang, and J. L. Wang, \"Hardware Implementation of FIR Filter Based on DA Algorithm\", Journal of PLA University of Science and Technology, vol. 4, pp. 22-25, 2003. [8] D. Wu, Y. H. Wang, and H. Z. Lu, \"Distributed Arithmetic and its Implementation in FPGA\", Journal of National University of Defense Technology, vol. 22, pp. 16-19, 2000. [9] L. Wei, R. J. Yang, and X. T. Cui, \"Design of FIR filter based on distributed arithmetic and its FPGA implementation\", Chinese Journal of Scientific Instrument, vol. 29, pp. 2100-2104, 2008.

Copyright

Copyright © 2024 Akriti ., Akshya Dwivedi, Akash Sharma, Aditya Swarnakar, Unnati . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.