Graph Theory in Social Media Related to Whatsapp

Abstract

Graphs are extensively used to model social structures based on different kinds of relationships between people or groups of people. WhatsApp media can conveniently be modelled using graphs, the connection between individuals in WhatsApp media can be described using graphs ranging from two individuals connected and communicating to different WhatsApp groups, this can be comfortably explained by graphs. The idea of directed graphs, undirected graphs and adjacent matrix as it’s related to WhatsApp groups has been presented.

Introduction

I. INTRODUCTION

The graph theory was introduced by the famous Swiss mathematician named Leonhard Euler, to solve many mathematical problems by constructing graphs based on given data or a set of points. The graphical representation shows different types of data in the form of bar graphs, frequency tables, line graphs, circle graphs, line plots, etc. Graph Theory is the study of points and lines. In Mathematics, it is a sub-field that deals with the study of graphs. It is a pictorial representation that represents the Mathematical truth. Graph theory is the study of relationship between the vertices (nodes) and edges (lines). Formally, a graph is denoted as a pair G (V, E). Where V represents the finite set vertices and E represents the finite set edges. Therefore, we can say a graph includes non-empty set of vertices V and set of edges E. Graph theory is also used in social networks to model the interactions between different people. This can be done by using a graph that determines how important a node (a person) is in an online community based on how many connections they have made with other nodes.

II. GRAPH THEORY

Graph Theory, in discrete mathematics, is the study of the graph. A graph is determined as a mathematical structure that represents a particular function by connecting a set of points. It is used to create a pairwise relationship between objects.

The graph is made up of vertices X (nodes) that are connected by the edges (lines). The application of linear graph are used not only in Maths but also in other fields such as Computer Science, Physics and Chemistry, Linguistics, Biology, etc. In real-life also the best example of graph structure is GPS, where you can track the path or know the direction of the road.

III. GRAPH THEORY IN SOCIAL MEDIAS

Even eminent figures such as the founder of Facebook, Mark Zuckenberg , have spoken of “social graphs” to represent the connections and relationships that users of the social network have. Graph theory is a branch of mathematics, the same branch that is also used in computer science. It is based on both discrete and applied mathematics.

For a few years now we can say that the increase in the use of social networks has been exponential, Facebook, Twitter, Instagram and LinkedIn are already part of our daily lives. In addition, social networks have become more important in terms of the creation and distribution of information. This means that the volume of information and its need for analysis has to be carried out in Big Data and Business Intelligence environments. In this way, it is possible to obtain prescriptive information for companies (such as information collected with the theory of graphs).

IV. WHATSAPP

WhatsApp (also called WhatsApp Messenger) is an internationally available freeware, cross-platform, centralized instant messaging (IM) and voice-over-IP (VoIP) service owned by American company Meta Platforms (formerly Facebook). It allows users to send text and voice messages, make voice and video calls, and share images, documents, user locations, and other content. WhatsApp's client application runs on mobile devices, and can be accessed from computers. The service requires a cellular mobile telephone number to sign up. In January 2018, WhatsApp released a standalone business app called WhatsApp Business which can communicate with the standard WhatsApp client.

The client application was created by WhatsApp Inc. of Mountain View, California, which was acquired by Facebook in February 2014 for approximately US$19.3 billion. It became the world's most popular messaging application by 2015, and had more than 2 billion users worldwide by February 2020. By 2016 it had become the primary means of Internet communication in regions including Latin America, the Indian subcontinent, and large parts of Europe and Africa.

V. GRAPH THEORY TERMINOLOGIES

A. Graph

A graph-generally denoted G (V, E) or G= (V, E) - consists of the set of vertices V unitedly with a set of edges E. The number of vertices in a graph is normally denoted n while the number of edges is normally denoted m.

1. A graph is a collection of vertices and edges that represents relationships
2. Vertices/Nodes correspond to objects in a network
3. Edges are the links between objects belonging to a network, edges of a graph might have weights indicating the strength of that link between vertices. Edges are denoted by E = (U, V) it is a pair of two vertices.
4. Graph theory is the study of graphs and their properties and a graph data structure has two basic elements: vertices and edges. We use the notation of G (V, E) meaning that the “Graph G with vertex set V and edge set E”.

a. Null Graph: It has zero edges and denoted by G = (V (G)) is a null graph, which is |E(G)|=0

b. Complete Graph:  A complete graph G = (V, E) is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.

c. The Degree of Vertex: The degree of vertex is the number of edges connecting in it.

d. Regular Graph: In a graph if all vertices have the same degree (incident edges) k than it is called a regular graph.

e. Cycle Graph: Cycle Graph or Circular Graph is a graph that consists of a single cycle. In a Cycle Graph number of vertices is equal to number of edges.

f. Source Vertex: Is a vertex with in-degree zero. Also, a vertex that has many out-degree with no number of in-degree.

g. Directed Graph: A directed graph in which represented by an ordered pair of two vertices, e.g. (V denotes an edge from   to   (from the first vertex to the second vertex).

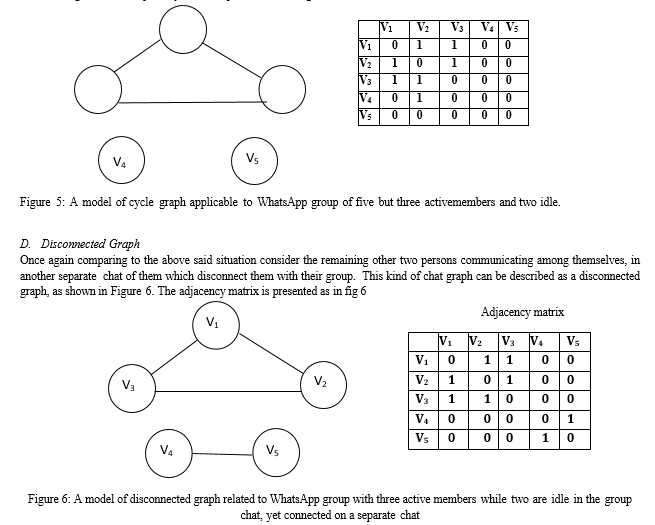
h. Disconnected Graph: A graph G is said to be disconnected if there exist two vertices, In G such that no edge in G has those vertices as endpoints.

VI. GRAPH MODELS OF WHATSAPP

Graphs are used in a wide variety of models. Graph theory is a robust tool for examining relationships between any set of people (objects) (Chuck Easttom, 2017). We are going to dwell on the description of how to construct Graph models of communications in social media networks. We shall be describing some diverse graph models for some interesting applications in WhatsApp groups. The reason behind using the graphical model in social networks is to describe the network more elaborately and systematically. This graph model allows us to describe the properties of the network elaborately and distinctly. The relation between the individuals can be mapped using the graphical method and how one can access the resources of other users can be described.

Communication needs both the sender and receiver. WhatsApp uses two types of communications like single sender many receivers. Many sender single receivers, many senders many receivers and so on. In WhatsApp, first, it shows the contact of the persons who are all using WhatsApp like us. These can be compared with the set of all vertices.

A. Edge

In WhatsApp when two people are friends in chat, it means they are connected. The relation between them can simply be model by a graph with an edge connecting two vertices V1 and V2 as shown in Figure 1. This kind of graph is known as the collaboration graph, where V1 and V2 are related and are working together in a particular way.

1. Null Graph: Let us consider 5 persons using WhatsApp. Then, the graph consists of 5 vertices as shown in Figure 2. When all the persons are idle, there is no communication and we say is related to a null graph, as shown in Figure 2, a WhatsApp group that is not active. In graph theory, if no edges are connecting the vertices, we say the group is idle

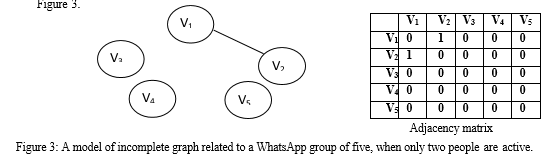
2. Incomplete Graph: In a group chat when only two persons are active in a chat while the others are inactive, it means the two are connected while all the other members of the group are inactive. In graph theory, this is described as an incomplete graph model. For example, we consider an edge between V1 and V2, as connected while all other vertices not connected shown in Figure 3.

B. Complete Graph

When all the persons needed to communicate are communicating at a time, then the WhatsApp group formed is complete and used. It can be related to a complete graph.

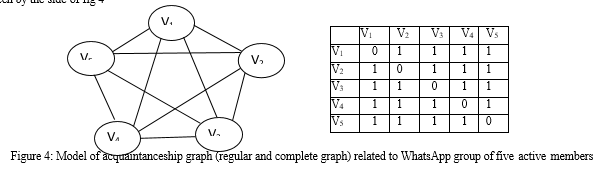
A WhatsApp group in which both the admin and all members of the group are allowed to send and receive messages can also be related to a complete graph as in Figure 4. Two vertices which are incident with a common edge are said to be adjacent. In a complete graph given in Figure 4, every vertex is adjacent to each other.

In WhatsApp group chat, where every person is connected to every other person, this can also be known as a complete active group. This can be referred to as a complete graph. Again referring to a group chat of 5 persons, where every person is connected to 4 other persons. In Graph Theory, this can be referred to as a regular graph, in which every vertex has the same degree. Figure 4 is an example of such a regular graph and is also called an acquaintanceship graph. The adjacency matrix of the graph is presented as seen by the side of fig 4

C. Cycle Graph

Once again, referring to a suppose three-person are active in a group chat, while the others are inactive their communication graph model is related to Cycle graph as in fig 5, V1, V2, and V3 are active while V4 and V5 are not active, this means that there is communication between three persons only and the other two persons are idle this can be referred to cycle graph with 3 vertices as shown in Figure 5. The adjacency matrix is presented as in fig 5

E. Directed Graph

Once again referring to a WhatsApp group of five persons in which three persons are communicating between themselves and the messages are directed to a particular person amongst them. When a group chat is inactive or idle and the group members are participating in a separate chat with each other as shown below. Suppose from the graph below that V1 sends a video message to V2. V2 opens the message and watches it and in turn, sends it to V 3, V3 open the message and send the same to V1 as shown in fig 7, this kind of connection is a typical directed graph model, this can also be called an influence graph. In studies of group behavior, it is observed that certain people can influence the thinking of others. A directed graph called an influence graph can be used to model this behavior. Again taking note of the situation stated above, this can be referred to as an influence graph and the adjacency matrix is presented as shown in fig.7

D.  Directed Graph

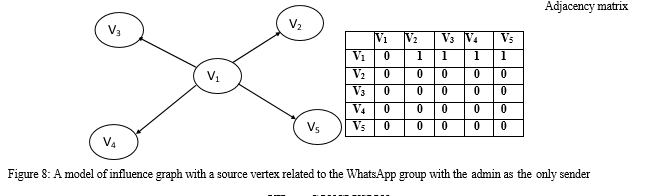
A WhatsApp group can be closed or open, but for our figure 8 it is closed that is no one in the group is allowed to send messages to the group except the group admin. This is a directed graph, unlike figure 8 it is the undirected graph and is open to all group members, they can all send and receive messages from each other without any constraints. However, all messages received are from a single sender many receivers, only the group admin has the right to send messages to the group, we can describe V1 as a source vertex because V1 has zero in-degrees as shown in fig 8. Again this is an influence graph model. The adjacency matrix is presented as in fig 8

VII. ACKNOWLEDGEMENT

Thank you to M. RAMYA, Assistant professor in Department of Mathematics at Dr SNS Rajalakshmi College of Arts and Science who has supported this research.

Conclusion

In this work, we focused on extracting the relevant information about relationships on social media networks precisely WhatsApp. Thus the relationship in WhatsApp has been discussed and also, modeled with the concept of graph theory. These techniques work on any graph, including the social graph. Thus the WhatsApp models of the graph have been discussed and also, related to the concepts of graph theory. The methodological focus of this research concentrated on relevant areas of operations research, including graph theory, network models that were shown to add insight into the analysis of social networks. The techniques developed in this paper, extend the existing operations research methods to the social network as model graphs.

References

[1] Dr. N.V. Muthu Lakshmi, L.T.Lakshmi praveena, A review of graph Based Algorithm in Social Media Data Analytics, February 2018, Volume 5, Issue 2. [2] Basadeb Mondal,A Comparison of Graph theory and Social Media Network, Volume 7, Issue 2(A); February 2020. [3] Murtaza.M.J Farooque, Formal Theory of use of social Networking sites in Academic Communiction, ISSN:716-5256. [4] Dmitri Golden berg, Social Network Analysis, From Graph Theory to Application with Python, 5 February 2021. [5] Anwesha Chakraborty, Application of Graph theory in Social Media, volume 6, Issue-10, Oct 2018.

Copyright

Copyright © 2022 Vidhyadharani K B, Ramya M. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.