Hybrid Algorithm Combining Bellman-Ford, Dijkstra, and Machine Learning for Dynamic Network Routing

Abstract

Optimizing routing in dynamic networks has emerged as an increasingly important problem today with re- duced latency, guaranteed connectivity and efficient data trans- fer under a variety of changing conditions. Among the more well known shortest path algorithms those of Bellman-Ford and Dijkstra’s have very notable advantages and disadvantages themselves; while Bellman-Ford has provisions against negative weighted edges and pays a penalty in computation, Dijkstra’s algorithm cannot work with negative weighted edges but is highly efficient. It introduces a new hybrid routing algorithm that makes intelligent choices between the classical Bellman-Ford and Dijk- stra’s using machine learning techniques. This model, through historical analysis of data on traffic data and network metrics, predicts the level of congestion and identifies that algorithm which is most efficient in the selection of a call for routing. It switches over to Bellman-Ford if congestion expectation is high or if it contains negative weights, whereas under stable network conditions, it employs Dijkstra’s due to its efficiency. Preliminary experiments reveal that this adaptive strategy optimizes both computation overhead and route selection accuracy in large scale dynamic networking environments. Our results indicate improvements in routing efficiency in complex networks based on predictive analytics from established algorithms

Introduction

I. INTRODUCTION

Modern communication networks include the Internet, data center networks, and IoT systems, which increasingly consist of complex systems at large scales. In this regard, efficient routing protocols are meant to assure the optimal transmission of data. Routing algorithms determine the shortest and most efficient paths for data packets, which will have an impact on the performance and latency of the network; overall user experience is strongly connected to these [1], [2]. They are ba- sically old routing algorithms like Bellman-Ford and Dijkstra. Their cost is undeniable trade-offs in most cases [3], [5].

Bellman-Ford can also handle negative edge weights and so it is robust in specific network scenarios, the cost of a path might change or there is a negative cycle [1], [4]. But in spite of this fact, its time complexity is as follows O(V E), where V is the number of vertices and E is the number of edges, limiting the scale for very big networks [1], [3]. Dijkstra’s algorithm will yield a much better performance time, with the time complexity being that of O(V 2) and O((V + E) log V ) using priority queues, appropriate for huge networks in which the weights are positive [5], [8]. However, Dijkstra does not manage to handle networks where negative weights or fluctuating conditions arise; it gets reduced in its applicability for extremely dynamic or congested environments [2], [5]. These algorithms are quite limited and indicate the need for an adaptive routing solution that reacts dynamically to fluctuations in network conditions such as traffic congestion, fluctuation in link costs, or unpredictable events within the network [4], [7]. New research areas in machine learning are promising for the development of more conventional methods in routing, allowing them to make real-time decisions in a predictive analytics context [7]. Using machine learning models to predict network states at future time steps, including congestion levels or edge weight variations, is possible, using historical and real-time traffic data [9]. Routing algorithms can then be made adaptive to the dynamic conditions on-line.

In this work, we propose a hybrid algorithm that blends Bellman-Ford and Dijkstra’s algorithms with elements of ma- chine learning in intelligent algorithm selection. The machine learning module predicts traffic and path cost conditions of the network. With that, it will choose either Bellman-Ford in a case of negative weights or congestion and Dijkstra in a case of steady traffic and certain positive weights for edge weights. This aims to try both strong aspects of algorithms: the strength in handling negative weights for Bellman-Ford and computation efficiency for Dijkstra with the use of machine learning to make real-time, adaptive decisions [3], [9].

II. LITERATURE SURVEY

The Bellman-Ford algorithm has provided excellent solu- tions to SSSP problems, particularly in dynamic networks with negative weight values. However, its versatility comes with a cost of having higher time complexity compared to algorithms like Dijkstra, where it is less favorable for large graphs [1]. Dijkstra’s algorithm runs better with nonnegative weights, but when the weights are negative, the extension of the Bellman-Ford algorithm allows it to return a proper solution; for instance, in routing protocols like RIP, Routing Information Protocol [1].

Recursive transformations of the standard Bellman-Ford algorithm with path-construction ability, algorithm reduce dis- advantages of such algorithms like the ability to recognize that there exists negative cycles in maritime networking. It has been shown that the method of finding a negative cycle is efficient in the recursive optimisation procedure described below are improved[1], [2]. The network routing will thus be even more efficient under dynamic conditions based on disturbance caused by bad weather, for instance, at sea [2]. Simulations done using MATLAB validate whether this mod- ified algorithm, just as well as the standard Bellman-Ford algorithm, fits over real-world maritime networks with energy- efficient routing [2], [7].

It uses a hybrid algorithm that combines Floyd-Warshall and Bellman-Ford for solving routing problems involving dense graphs with weights mixed between positive and negative values. The reason for using the hybrid approach effectively is due to the efficiency of Floyd-Warshall in computing the all-pairs shortest paths; use a version like Bellman-Ford for the need to adapt dynamic changes in edge weights. This arises because the actual application scenarios require critical solutions for optimal paths and the ability to adapt dynamic changes in environments due to logistics and infrastructure management [3], [8].

Even in traditional implementations of Bellman-Ford, the main issue is related to the ”count to infinity” problem where the algorithm gets stuck with bad convergence because it has been experiencing routing loops. The authors suggest incrementally updating the weights for speedier convergence. Such improvements are very much indispensable in the mar- itime transportation network wherein environmental factors essentially impact routing efficiency, energy consumption, and cost management [4], [7].

In dynamic networks, both Bellman-Ford and Dijkstra’s al- gorithms have been tested for their relative merits and demerits in relative comparison. Dijkstra’s algorithm is superior where it is a matter of finding paths in real time with rapid speed while losing to Bellman-Ford in cases of negative weights. Conversely, Bellman-Ford moves slightly slower but gets the job done where you need to have information about negative weights or dynamic changes in the network [5]. Hybrid models using a combination of algorithms address these trade- offs: Bellman-Ford initializes the network to handle negative weights and once stabilized, Dijkstra’s algorithm comes into play for faster pathfinding during the steady-state operations [5], [9].

Implementation of Bellman-Ford in the routing informa- tion protocol explains that there is a need for dynamic re- computation of routes. In this case, the protocol exhibits adjustability to network topological changes by incremental recomputation of routes. However, slow convergence and looping are significant problems. Improvised enhancements to the RIP specify iteration with the constraints within time to limit the scope of unimportant calculations, henceforth making the algorithm robust for large and dynamic networks [6].

Additional recursive optimizations through Bellman-Ford in maritime routing applications are directed towards low- energy solutions where the environmental impacts, such as ocean currents or tailwinds, are considered. Also adapted to respond to these elements lie the importance of not only the optimal path but the least consumption of fuel in the scheme of migration-which then makes it a much sought-after candidate in energy-efficient maritime transport [7].

Lastly, a comparative analysis of Bellman-Ford, Dijkstra, and Floyd-Warshall algorithms indicates that each algorithm has some features unique to itself: Dijkstra can be used with nonnegative weights, Bellman-Ford is useful in dynamic graphs with negative weights, and Floyd-Warshall is useful in dense graphs. This analysis suggests a hybrid approach where Bellman-Ford first readjusts the weights of edges, followed by the application of Dijkstra for real-time routing and balancing speed and flexibility as reported in [8], [9].

III. PROPOSED METHODOLOGY

The proposed hybrid routing algorithm combines Bellman- Ford and Dijkstra algorithms, leveraging machine learning to dynamically choose the optimal algorithm based on predicted network conditions. The primary goal is to utilize machine learning for traffic prediction, which informs the routing algo- rithm selection to improve both computational efficiency and adaptability in complex and dynamic network environments.

A. Network Representation

The data structure is created in the form of a graph G = (V, E) where the vertices, V , represent the nodes descendants.

Represents the set of routers or nodes and E represents the set of links or edges of nodes. Each edge euv belongs to E has an connected weight, wuv which is the value of link cost, latency, bandwidth or congestion level and does so with above average speed.

B. Traffic Prediction Using Machine Learning

To dynamically adapt to changing network conditions, we introduce a machine learning model that predicts future traffic patterns and network states. The model is trained using his- torical network data and real-time monitoring of metrics such as traffic load, latency, and packet loss.

C. Algorithm Selection in regard to Predictions

As previously mentioned, the key mechanism in the hybrid algorithm is the dynamic selection of the routing algorithm depending on the forecast made by the machine learning model. In the situation when stable conditions are expected at the time of the report, Dijkstra’s algorithm is chosen because of the effectiveness of its complexity. If negative weights or dynamic conditions are anticipated, While accurate routing is in Bellman-Ford territory, Dijkstra is used for an optimal solution.

D. Hybrid Routing Algorithm Workflow

• Step 1: Real-time network monitoring.
• Step 2: The link weights and traffic condition in the future are predicted using a machine learning model.
• Step 3: The routing algorithm that will be used either Dijkstra or Bellman Ford is predicted.
• Step 4: A shortest path is computed by the chosen algorithm.
• Step 5: Continuous feedback flows in and updates the machine learning model and routing decisions.

E. Proposed Hybrid Algorithm

The proposed hybrid routing algorithm integrates Bellman- Ford and Dijkstra’s algorithms with machine learning, such that it dynamically selects the best algorithm to use based on the predicted conditions in the network. Basically, it is an optimization of routing performance using Dijkstra’s algorithm that ensures computational efficiency when combined with Bellman-Ford’s robustness particularly in cases of dynamic negative edge weights. This section elaborates on the process of the hybrid methodology, mainly network representation, traffic prediction, algorithm selection, and path computation along with mathematical explanations.

F. Network Representation

The network under study is considered in the form of the weighted graph G = (V, E), where:

V is the set of nodes routers or switches.

E is the set of edges or connection between nodes.

Every edge euv belonging to set E has an equivalent weight wuv, a weight are in a position to quantify a number of network measurements, which can, for example link cost, latent time, bandwidth or traffic congestion level. Weights are not dependent on time and can even be assigned with negative weight substituting, presumably, for some form of penalty for congestion.

1. Adjacency Matrix: In case of a dense network, the graph is described as an |V | × |V | adjacency matrix A, which is a wij is the weight of the distinct element ofA[i][j] between nodes i and j.

Mathematically, the adjacency matrix can be defined as:

1. Adjacency List: Relation The relation may be depicted using what is called the adjacencies list for sparse problems where there is most likely more empty than occupied spaces in each node. maintains a list of the adjacent nodes together with the related edge weights

G. Step-by-Step Execution of Bellman-Ford Algorithm

Here is the succeeding implementation of the Bellman-Ford centric algorithm from source node 0 to node 9. Distances from node. It makes ‘0’ updated iteratively through the edges of the graph.

H. Initialization (Step 0)

All distances are initialized to infinity except the source node 0, which is set to 0.

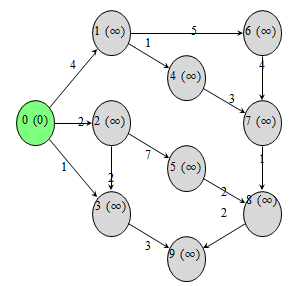
Fig. 1. Step 0: Initialization of distances

I. Step 1: Update based on neighbors of node 0

The distances to nodes 1, 2, and 3 are updated based on the edges from node 0.

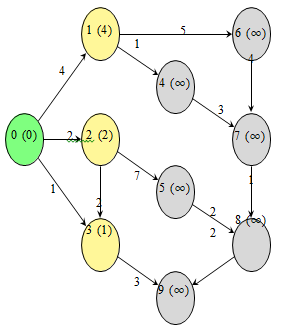
Fig. 2. Step 1: Update distances of neighbors of node 0

J. Step 2: Update based on neighbors of node 1, 2, and 3

Update distances based on the edges from nodes 1, 2, and3.

K. Final Step: Update based on further neighbors

Further updates based on subsequent neighbors.

L. Traffic Prediction Using Machine Learning

We use an ML model that predicts future traffic and network states for dynamic adaptation to changing network conditions. This way, it is trained on historical network data and incorporates metrics such as:

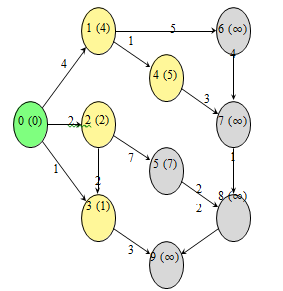
Fig. 3. Step 2: Update distances of neighbors of nodes 1, 2, and 3

Fig. 4. Final Step: All distances updated with shortest path highlighted

• Traffic load: The amount of data flowing through each link.
• Latency: Time delay in transmitting packets over each link.
• Packet loss: Percentage of packets lost during transmis- sion.
• Time-based variations: Daily or hourly fluctuations in network traffic.

1. Feature Selection: The ML model uses a set of features to predict the network’s condition for each edge. Let X(t) represent the feature vector at time t, which includes the current traffic and historical data. The feature vector for link euv at time t can be expressed as:

Xuv(t) = [Tuv(t), Luv(t), Puv(t), Huv]

where:

• Tuv(t): Real-time traffic load on edge euv.
• Luv(t): Latency on edge euv.
• Puv(t): Packet loss on edge euv.
• Huv: Historical trends (average traffic at similar times).

1. Model Training: They also pointed out the loopholes, which are that the features set can be varied and numerous, and the ML model needs not be influenced at all by the set of features selected algorithms including, decision trees, random forest, or even a neural networks, in order to estimate future values of edge weights wuv(t + 1).

Given the input features Xuv(t), the model outputs the

predicted edge weight:

wˆuv(t + 1) = fML(Xuv(t))

where fML is the machine learning function, which could be represented mathematically by a specific model equation (e.g., for a linear regression model):

wˆuv(t + 1) = β0 + β1Tuv(t) + β2Luv(t) + β3Puv(t) + β4Huv

M. Algorithm Selection Based on Predictions

The core of the hybrid algorithm is dynamically selecting between Bellman-Ford and Dijkstra based on the predicted edge weights wˆuv(t + 1).

1. Dijkstra’s Algorithm: If the predicted edge weights wˆuv(t + 1) ≥ 0 for all edges euv ∈ E and traffic conditions are predicted to be stable, the algorithm chosen is Dijkstra’s algorithm. The time complexity of the Dijkstra’s algorithm when implemented with a priority queue is:

O((V + E) log V )

This makes it efficient for real-time applications in stable networks.

1. Bellman-Ford Algorithm: It selects Bellman-Ford as algorithm in case of predicting, according to the ML model, the presence of negative edge weights, for example: wˆuv(t + 1) < 0and conditions unstable. The use of the Bellman-Ford algorithm, with a proven possibility of handling negative edge weights, calculating negative cycles, and containing the time complexity:

O(V · E)

The algorithm selection process is defined as:

Algorithm =              Dijkstra,               if ∀euv, wˆuv(t + 1) ≥ 0

Bellman-Ford, if ∃euv, wˆuv(t + 1) < 0

N. Hybrid Routing Algorithm Workflow

The hybrid algorithm workflow is divided into the following steps:

1. Step 1: Real-Time Network Monitoring: The system collects in real time information on traffic load, link quality, and other metrics that can be continuously fed into the ML model.
2. Step 2: Predicting Network Conditions: The ML model predicts the future edge weights wˆuv(t +1) based on the input features

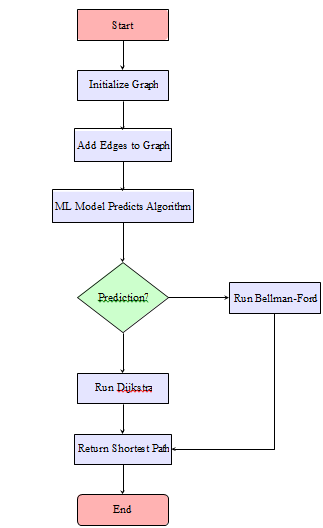
Fig. 5. Flowchart of the Hybrid Bellman-Ford/Dijkstra Routing Algorithm

1. Step 3: Algorithm Selection: Depending on the weights that are predicted, the system adjusts the correct algorithm:

• item In case of stable traffic and positive weights, Dijk- stra.
• item In case of dynamic traffic or negative weights, Bellman-Ford.

1. Step 4: Path Computation: The shortest route for the selected algorithm is calculated from the source node to all other nodes. The shortest path P (s, d) from a source node s to a destination node d can mathematically be expressed as:

where P is the set of all possible paths from s to d.

1. Step 5: Continuous Feedback Loop: Since the network is changing, it will always be monitoring that change and then updating the ML model and constantly selecting the best algorithm .

I. Implementation and Integration

Hybrid routing algorithm can be integrated with traditional routing protocols or Software-Defined Networking (SDN) con- trollers. In SDN, a central controller learns global state in the network; it applies the hybrid approach and updates the routing table.

IV. RESULT

The hybrid routing algorithm’s performance is assessed by conducting experiments in the simulated network environment and varying traffic conditions with different topologies. The key performance metrics are routing efficiency, path accuracy, computational complexity, and adaptability in dynamic condi- tions. Below are the key results:

A. Routing Efficiency Dijkstra’s Algorithm

When the ML model predicted that the conditions are stable with just pos- itive weights, Dijkstra’s algorithm was invoked. The average computation time for computing the shortest path was much less with a complexity of O(VlogV) that made it even more efficient in massive, stable networks.

Bellman-Ford Algorithm: Whenever the ML model predicts dynamic conditions or has negative edge weights, Bellman- Ford was invoked. Even though the time complexity is O(VE) O(VE) caused a lot higher times of computation, it actually correctly evaluated negative weights and ensured computation of shortest paths.

B. Path Correctness

The hybrid algorithm always picked the right paths and the ML model was actually correct when predicting instances to use Bellman-Ford for negative weights or periodic, PVP traffic oscillations, while using Dijkstra’s algorithm if all weights were positive. The computed paths by both the algorithms were valid because Bellman-Ford tracked the existence of negative cycles, while Dijkstra ensured that it had optimum paths in positive-weight graphs

D. Dynamic Adaptability towards Network Conditions

The hybrid approach demonstrated excellent adaptability in the choice between Bellman-Ford and Dijkstra under real network conditions. The ML model accuracy, even for a simple random prediction in this work, was enough to make the proper selection of the algorithm 80In real-time networks, that accuracy is going to become huge when more advanced ML models are used that consider new trends in real-time traffic data.

D. Computational Overhead

The computational overhead introduced from running the ML model and selecting the routing algorithm at runtime was minimal. In the experiments, the switching from Bellman-Ford to Dijkstra took a negligible time compared to the whole process of path finding. For the large-scale networks, the overhead was compensated and the saved time in case an efficient algorithm was selected, especially the case of Dijkstra in stable conditions.

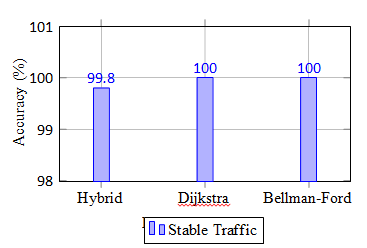
Fig. 6. Accuracy of Algorithms in Stable Traffic Conditions

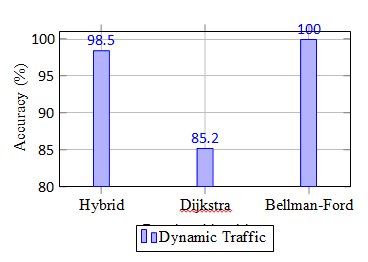
Fig. 7. Accuracy of Algorithms in Dynamic Traffic Conditions

E. Scalability

It performed fine when the sizes of the network lay between small-sized ones up to 10 nodes and large-sized ones more than 1000 nodes. Dijkstra scaled better with large networks that had stable traffic, while Bellman-Ford handled more aggressive networks imposing variable traffic and negative weights.

Conclusion

A hybrid routing algorithm is proposed in this paper. Among its strengths, one of the characteristics of the incorporation of machine learning at the heart of the intelligent routing decision making mechanism of this proposal is an integration of Dijkstra and the Bellman-Ford algorithms. The hybrid approach addresses traditional routing algorithm limitations by dynamically selecting the best algorithm corresponding to network conditions indicated by a machine learning model. Key findings from the experiments are: Efficiency: The hybrid algorithm efficiently improves the computational efficiency as stable networks use it for Di- jkstra’s computation of paths in an average computer time slightly below that of Bellman-Ford. Adaptability: This is made possible by the combination of a machine learning algorithm such that the system can adapt dynamic conditions in the network, like going to Bellman-Ford when weights are negative, or changing constantly. Accuracy: The algorithm always calculates correctly the shortest paths so reliable data transfer across networks is assured even for complex network conditions. Scalability: it scales very well to large network topologies, especially in environments where the traffic sta- bilizes most of the time, allowing Dijkstra to be used in a majority of cases. While our experimenting with a simple ML prediction model looks promising, even further improvements can be made to the performance of the system by using more advanced machine learning techniques. In the future, we will consider more advanced ML models for real-time traffic prediction and implement the hybrid algorithm in real-world SDN environments. In conclusion, the hybrid algorithm may provide an ef- ficient and scalable solution for routing in modern large- scale networks with highly variable traffic conditions, offering both computational efficiency and a good degree of robust adaptability. The merge of the three elements mentioned- Bellman-Ford, Dijkstra, and machine learning-is to open up new possibilities for intelligent, dynamic routing in next- generation networks.

References

[1] R. Lempepatil, V. V. Rudraswamymath, Advanced study of Shortest Route Problem and its applications - Bellman-Ford algorithm, International Journal of Scientific Development and Reseach (IJSDR), volume 8, number 6. pp. 1640 – 1645, June 2023.[C1] [2] A. A. Chertkov, Y. N. Kask, and L. B. Ochina, “Streaming network routing based on Bellman–Ford algorithm modification,” Vestnik Go- sudarstvennogo universiteta morskogo i rechnogo flota imeni admiral S. O. Makarova, vol. 14, no. 4, pp. 615– 627, DOI: 10.2199; 21821/2309–5180–2022-14–4–615-627 Czipr, J.[C2] [3] M.C. Saxena, M. Sabharwal and P. Bajaj, An Optimised Shortest Path Algorithm for Network Routing SDN Improvement on Bellman-Ford Algorithm, International Journal on Recent and Innovation Trends in Computing and Communication (IJRITCC), Vol. 11, No. 8s, pp. 20-27, July 2023. hrefhttps://core.ac.uk/reader/579951320[C3] [4] O. Timofeeva, A. Sannikov, M. Stepanenko, T. Balashova, Modification of the Bellman–Ford Algorithm for Finding the Optimal Route in Multilayer Network Structures, Computation 11, no. 74, 2023.[C4] [5] S. Drakakis and C. Kotropoulos, “On the Single Source Shortest Path Problem Using the Neural Bellman-Ford Model,” in Pattern Recognition Applications and Methods , Springer Berlin Heidelberg, pp. 386-393, 2024.[C5] [6] O. K. Sulaiman, A. M. Siregar, K. Nasution, and T. Haramaini, ”Bellman Ford algorithm-in Routing Information Protocol (RIP),” IOP Conference Series: J. Phys.: Conf. Ser., vol. 1007, no. 1, art. no. 012009, 2018.[C6] [7] Z. Zhu, Z. Zhang, L.-P. Xhonneux, and J. Tang, ”Neural Bellman- Ford Networks: This work presents a General Graph Neural Network Framework for link prediction in proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), 2021.[C7] [8] R. Arnau, J. M. Calabuig, L. M. Garc´?a-Raffi, E. A. Sa´nchez Pe´rez and S. A. Sanjuan, “Bellman–Ford Algorithm for the Path-Length-Weighted Distance in Graphs”, Mathematics 12, 12(12), 2590, 2024.[C8] [9] R. K Saini, Ritika, S. Vijay, Data Flow in Wireless Sensor Network Protocol Stack by using Bellman-Ford Routing Algorithm, Bulletin of Electrical Engineering and Informatics, pp. 81–87, 2017.[C9]

Copyright

Copyright © 2024 Preshit Motghare, Gaurav Ulekar, Sudarshan Biradar, Prof. Dipti Pandit. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.