Image Colorization using CNN

Abstract

It is indeed a challenging task to determine the originality of an image presented in grayscale format. In this paper, we aim to restore the image to its original color. We will utilize machine learning algorithms, trained on thousands of samples, to accurately colorize the input image. The system functions as a feed-forward pass in a CNN during the testing phase, utilizing a training set of over one million color images. To evaluate our algorithm, we conduct a “Colorization Turing test,” where participants are tasked with distinguishing between generated color images and original ones. Our method success- fully deceives participants 32% of the time, marking a substantial improvement over prior technique. Additionally, we demonstrate that the colorization process can be an effective tool for self- supervised feature learning by acting as a cross-channel encoder, achieving leading results on several feature learning benchmarks.

Introduction

I. INTRODUCTION

Image colorization is the process of adding color information to a grayscale image. Convolutional Neural Networks (CNNs) are an important aspect of the colorization of an image as they help us to extract the hierarchical features of an image based on which we can colorize the image. The network’s work is determining chrominance information from the input image pixels while maintaining luminance. This prediction occurs within the Lab color space, where the L channel represents lightness, and the a and b channels encode color. Regularization techniques like dropout are often applied to prevent overfitting. Once trained, CNNs perform colorization as a feed-forward pass, generating realistic colors based on learned features. The supervisory signal in earlier colorization techniques is often provided by the ab channels, whereas the L channel of a picture is employed as input. Because training data for convolutional neural networks (CNNs) is easily accessible, numerous methods have been used to predict colors from big datasets. Nevertheless, the output from earlier models was frequently desaturated and muted. This is partially because their loss functions, which, like in conventional regression tasks, encourage cautious predictions by concentrating on minimizing the Euclidean error between anticipated and real colors. Using a loss function created especially for colorization, our method is different. Prior research has indicated that color prediction is intrinsically multimodal, meaning that numerous objects may yield multiple legitimate color outcomes. For instance, the sky may be pink, purple, or blue, but it is not like that.

II. LITERATURE REVIEW

Zhang et al. (2016) present a novel fully automatic approach to image colorization using deep convolutional neural networks (CNNs). They address the inherent ambiguity of colorizing grayscale images by treating it as a classification task rather than regression, predicting a distribution of plausible colors for each pixel. The authors incorporate class rebalancing techniques during training to emphasize rare colors, improving the vibrancy and diversity of the results. In their experiments, they trained the model on over a million images from ImageNet, showing that their method outperforms previous approaches, particularly in avoiding desaturated colors. They evaluate their results through a "colorization Turing test," where human observers are asked to distinguish between real and colorized images, successfully fooling them 32% of the time. This was a significant improvement compared to prior methods. The authors also explored the use of colorization as a self-supervised learning task, demonstrating that their model learns useful feature representations for other tasks like object classification. The CNN trained on colorization achieved competitive performance on benchmarks like ImageNet classification and PASCAL VOC segmentation tasks. They further compared their model with concurrent works, demonstrating better generalization and vibrant, perceptually realistic results on legacy black-and-white photos.[4]

Anwar et al. (2022) conducted a comprehensive survey of deep learning techniques in image colorization, aiming to address the challenge of restoring RGB colors to grayscale images. The paper categorizes colorization methods into seven types based on architecture, input, and output. The authors identify key elements influencing the success of colorization models, including dataset limitations and evaluation metrics. To address these challenges, they introduce the "Natural-Color Dataset" (NCD), a benchmark tailored to image colorization.

Their experimental tests on both existing and the new dataset showed that deep learning models outperform traditional methods in generating vibrant and contextually appropriate colorizations. The paper benchmarks various deep learning models and highlights the use of Generative Adversarial Networks (GANs) for improved colorization quality. The authors also point out that despite advancements, many models still struggle with unusual colors and biased training data. Future directions include addressing the dataset limitations, improving training protocols, and incorporating new architectures for more natural results. Their systematic evaluation sets a foundation for future research, emphasizing the need for better data and feature learning.[6]

Deshpande et al. (2017) introduced a framework for learning diverse image colorization using a Variational Autoencoder (VAE) and Mixture Density Network (MDN) to generate multiple plausible colorizations for grayscale images. Unlike prior methods that produced only the most probable colorization, their model can generate multiple diverse outputs that maintain spatial coherence and avoid pixel-wise inconsistency. The authors developed a low-dimensional embedding of color fields via VAE, which helps generate realistic colorizations by preventing over-smooth or blurry outputs. They tested their model against conditional variational autoencoders (CVAE) and conditional generative adversarial networks (cGAN), showing superior performance in producing diverse and realistic colorizations. Their experiments involved three datasets—Labeled Faces in the Wild (LFW), LSUN-Church, and ImageNet-Val. Their model achieved lower errors and higher diversity compared to baseline methods. For instance, their method achieved better mean absolute errors in pixel color estimation and outperformed other methods in generating vivid and spatially coordinated color fields. The study concluded that their approach could be extended to other vision tasks requiring multiple predictions?.[3]

Žeger et al. (2021) provided a comprehensive review of grayscale image colorization methods, classifying them into three main categories: scribble-based, example-based, and deep learning methods. The authors highlighted how deep learning has transformed colorization, allowing for greater automation and improved image quality through neural networks. They reviewed algorithms from Iizuka et al. (2016), Zhang et al. (2016), Levin et al. (2004), and others, comparing their effectiveness based on metrics like PSNR and SSIM. Their tests on natural images demonstrated that user-guided neural networks, combining manual input with machine learning, produced the most visually convincing results. Despite the progress, challenges remain in accurately evaluating colorization quality due to the subjectivity of color perception. The authors suggest that future research should focus on refining loss functions and incorporating global and local image features for better performance.[7]

Sousa et al. (2012) presented a machine learning approach for automatically colorizing grayscale images using a colormap derived from a training image. Their method works on a per-pixel basis, extracting local features like SURF descriptors, FFT magnitude, and localized statistics, and uses support vector machines (SVMs) for color classification. They implemented a color-space discretization step using k-means clustering to reduce the number of colors in the image, followed by a graph-cut algorithm to align color boundaries with intensity edges for better color consistency. Experimental results show that their method can assign aesthetically believable colors, although it struggles in regions with few texture features, such as skies or flat surfaces. They tested the approach on various images, including landscapes and animal subjects, and demonstrated reasonable performance, especially in scenes with distinct textures. While the algorithm showed promise, the authors noted the need for incorporating global image information for further improvement.[8]

Luan et al. (2007) presented an interactive system for colorizing natural images with complex scenes. Their method divides the process into two stages: color labeling and color mapping. During color labeling, pixels with similar intensities and textures are grouped into coherent regions, with a new labeling scheme that considers both neighboring and remote texture features. In the color mapping stage, vivid colors are applied to a few pixels within each region, generating realistic results. The system is user-friendly, requiring only modest input, and offers real-time feedback. Their tests demonstrated effective colorization with minimal user interaction, significantly improving over prior methods. The framework was validated by comparing it with other colorization techniques, highlighting its ability to handle textured images more efficiently.[9]

Su et al. (2020) presented a method for instance-aware image colorization to improve the performance of colorizing complex scenes containing multiple objects. They identified a gap in existing learning-based colorization methods, which often fail to handle images with multiple objects due to a lack of clear figure-ground separation. To address this, they introduced a novel architecture combining an object detector with two neural networks: one for instance-level colorization and another for full-image colorization. These networks extract features at both levels and fuse them through a feature fusion module. The authors tested their approach on three large datasets—ImageNet, COCO-Stuff, and Places205—showing that their model outperformed existing methods in metrics like PSNR, SSIM, and LPIPS. Ablation studies confirmed the importance of instance-level learning and feature fusion for improved accuracy.

The method proved particularly effective in colorizing scenes with multiple, overlapping objects, yielding globally consistent results across various datasets. Their tests also included a user study, further supporting the model's superiority in user-preferred colorization results.[10]

III. METHODOLOGY

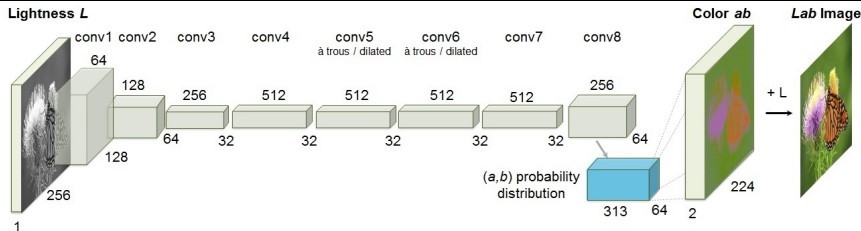
Fig 1. Convolutional Layers [4]

Alongside our research, Larsson et al. [11] and Iizuka et al. [12] have introduced similar systems that utilize large-scale datasets and convolutional neural networks (CNNs). Their approaches vary in CNN architecture and the choice of loss functions. In our work, we implement a classification loss that rebalances rare classes, whereas Larsson et al. opt for an unbalanced classification loss, and Iizuka et al. employ a regression loss.

Additionally, we investigate colorization as a method of self-supervised representation learning, where raw data serves as its own supervisory signal. This concept of learning feature representations is rooted in techniques such as autoencoders [4]. More recent studies have examined feature learning through data imputation, where predictions are made for a subset of withheld data (e.g., [3], [4], [7], [9]). Our approach aligns with this trend and can be described as a cross-channel encoder. We evaluate our model’s performance on generalization tasks in comparison to earlier self-supervised algorithms [4] and other concurrent methods [11], [12]. Remarkably, our method demonstrates strong performance, achieving state-of the-art results across several evaluation metrics.

IV. COLORIZATION TECHNIQUES

We train a convolutional neural network (CNN) to transform grayscale inputs into a distribution of quantized color values, utilizing the architecture depicted in Figure 2. Detailed architectural specifications can be found in the supplementary materials on our project webpage, and the model is publicly accessible. In this section, we will concentrate on the design of the objective function and our method for deriving point estimates of color from the predicted color distributions.

A. Objective Function

Given an input lightness channel X ∈ R H×W×1 , our goal is to establish a mapping Yb = F(X) to the two corresponding color channels Y ∈ R H×W×2 , where H and W represent the image dimensions. (Predictions are denoted with a ˆ symbol, while ground truth values are not.) This mapping is performed within the CIE Lab color space, as distances in this space effectively represent perceptual differences. A commonly used objective function, as noted in previous works, is the Euclidean loss L2(·, ·) between the predicted and actual colors:

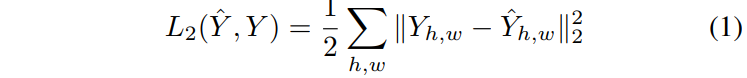
However, this loss function is not sufficiently robust to the inherent ambiguities and multimodal characteristics of the colorization task. When an object can possess a range of distinct ab values, the optimal outcome derived from the Euclidean loss tends to be the average of these values. In color prediction, this averaging can lead to grayish and desaturated results. Moreover, if the collection of possible colorizations is non-convex, the resultant solution may fall outside the feasible set, yielding precise outcomes.

Instead of approaching the problem as a regression task, we consider it as a multinomial classification challenge. We discretize the ab output space into bins with a grid size of 12, retaining Q = 256 values that lie within the color gamut, as illustrated in Figure 3(a). For a given input X, we learn a mapping Zˆ = G(X) that generates a probability distribution over the possible colors, where Zˆ ∈ [0, 1]H×W×Q, and Q represents the number of quantized ab values.

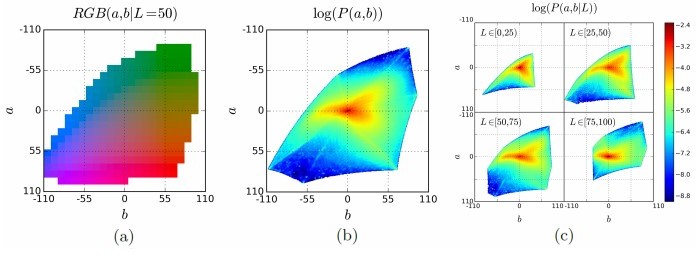
Fig. 2. (a) Quantiazed color space ab (b) [4]

To illustrate, suppose the grayscale input X corresponds to an image of a sky. The model predicts the distribution Zˆ which might suggest several possible color options, such as:

• Blue (with a high probability)

 • Light blue (with a moderate probability)

 • Pink (with a low probability)

To assess the predicted distribution Zˆ against the ground truth, we define the function Z = H −1 gt (Y ), which transforms the ground truth color Y into vector Z using a soft-encoding scheme. For instance, if the true color of the sky in the image is a bright blue, the corresponding vector Z may look like this:

Z = [0.8 (Blue), 0.1 (Light Blue), 0.05 (Pink), . . .]

indicating that blue is the primary color.

We then employ the multinomial cross-entropy loss Lcl(·, ·), defined as:

 (2)

where v(·) serves as a weighting term that can adjust the loss to account for the rarity of different color classes, as elaborated in Section 2.2. For example, if we observe that the color pink occurs less frequently in the dataset, we might assign it a higher weight to ensure the model learns to predict it accurately.

Finally, we convert the probability distribution Zˆ into color values Yˆ using the function Yˆ = H(Zˆ), which will be discussed further in Section 2.3. For example, the mapping might yield the final color output as a vibrant sky blue, given the high probability assigned to that color in the predictions.

B. Class Rebalancing

In natural images, the distribution of ab values tends to lean towards lower values due to the common occurrence of backgrounds like dirt, walls, and various surfaces. For example, Figure 3(b) displays the empirical distribution of pixels in the ab color space, derived from a dataset of 1.5 million images. It is apparent that the frequency of desaturated colors significantly exceeds that of more saturated hues.

As an illustration, consider a dataset of urban scenes where shades such as light gray (desaturated) are far more prevalent compared to bright colors like vibrant orange (saturated). Neglecting this imbalance could lead to a loss function that is overly influenced by these common, desaturated values.

To tackle the imbalance between color classes, we adjust the loss function during training by reweighting the pixel contributions based on their rarity in color representation. This approach is comparable to traditional techniques such as resampling the dataset. Each pixel is assigned a weight w ∈ R Q, which is determined by its proximity to the corresponding ab bin.

(3)

The weight w can be formulated as:

 (4)

To construct a smoothed empirical distribution pe ∈ ?Q, we first estimate the empirical probability of colors in the quantized ab space p ∈ ?Q using the entire training set. We then apply Gaussian smoothing with a kernel Gσ and combine this with a uniform distribution, adjusting the mix with a weight λ ∈ [0, 1]. The combined distribution is then inverted and normalized to ensure the expected weighting factor sums to one. Our experiments found that values of λ = 1/4 and σ = 6 were effective.

For instance, when employing this rebalancing technique, the model demonstrated improved predictions for saturated colors such as deep blue or rich red, which are typically less represented in the dataset. In contrast, without this rebalancing strategy, the model’s predictions tended to favor more muted tones like beige or taupe.

We will conduct a comparative analysis of the model’s performance with and without the implementation of class rebalancing, to illustrate the influence of this approach.

C. Mapping Class Probabilities to Point Estimates

We define a function H that converts the predicted distribution Zp into a point estimate Yp in the ab color space. One common approach is to select the mode of the predicted distribution for each pixel. This method can produce vivid colors but may lead to spatial inconsistencies, such as bright patches observed on specific objects like buses or flowers. For instance, when applying this method to an image of a red bus, the vibrant red might appear as splotches rather than blended seamlessly with the surrounding colors.

Alternatively, calculating the mean of the predicted distribution yields more spatially uniform results, albeit often resulting in desaturated colors. These outcomes can give the images an unnatural tone, reminiscent of sepia photography. This phenomenon arises because averaging after classification can inherit some issues similar to optimizing for a Euclidean loss in a regression context.

To achieve a balance between the vibrancy of the mode and the consistency of the mean, we can interpolate by adjusting the temperature T of the softmax distribution and subsequently calculating the mean of the adjusted results. Inspired by simulated annealing techniques, we refer to this process as obtaining the **annealed mean** of the distribution:

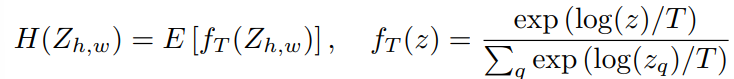
  (5)

When T = 1, the distribution remains unchanged. Reducing T leads to a sharper distribution, while as T approaches zero, the output becomes a 1-hot encoding corresponding to the mode of the distribution. Our experiments indicate that a temperature setting of T = 0.45 effectively captures the vibrancy associated with the mode while preserving the spatial coherence characteristic of the mean.

Overall, our system F comprises a convolutional neural network (CNN) G that generates a predicted distribution across all pixels, combined with the annealed mean operation H to yield the final predictions. Although the overall system is not fully end-to-end trainable, it is noteworthy that the mapping H operates independently on each pixel using a single parameter, allowing for straightforward integration into the feed-forward phase of the CNN. By maintaining this structure, we enhance the capability to produce visually appealing outputs while effectively managing color representation in the generated images.

V. RESULT

We evaluate our complete algorithm against a number of variations as well as current work. We evaluate colorization as a technique for self-supervised representation learning in the second sub Section. Lastly, we present qualitative examples of legacy black and white images.

A. Evaluating Colorization Quality

The colorization results for 10k images from the ImageNet validation set, which were     previously used in another study, are displayed in the table. The area under the curve (AuC) of the cumulative error distribution in the ab color space is given in the second column. The classification accuracy following colorization, as determined by the VGG-16 network, is displayed in the third column. The AMT real vs. fake test results, including the mean and standard error (estimated using bootstrap), are shown in the fourth column. It's significant to remember that 50% performance in the real vs. fake test is expected for an algorithm that generates perfect ground truth images. All metrics show that higher values are preferable. The descriptions of the various algorithms that each row relates to are given in the main text.

1. Perceptual Realism (AMT): The degree to which colors seem realistic to a human observer is the true test of colorization quality in many applications, especially computer graphics. We used Amazon Mechanical Turk (AMT) to administer a real vs. fake two-alternative forced choice test in order to assess this. In this experiment, subjects were shown pairs of images, one of which was a color photo in the original format and the other of which had been recolored using either a baseline model or our algorithm. The participants had to decide which of the two images they thought had computer-generated colors. Every picture, each with 256 x 256 pixels of resolution, was shown for one second. Participants were given an indefinite amount of time to decide after seeing each pair.
2. Semantic Interpretability (VGG Classification): Whether our approach generates colorizations realistic enough to be understood by a commercial object classifier is a crucial question. We employed a pre-trained VGG network, which was initially trained to identify real color images from the ImageNet dataset, to test this. We can assess whether the generated colors are accurate enough to offer useful information for object classification by feeding our colorized images into the VGG classifier. We know that our colorizations retain enough semantic information if the classifier performs well. Previous research has proposed using pre-trained classifiers to evaluate the generated data realism.
3. Raw Accuracy (AuC): We compute the percentage of predicted pixel colors in the ab color space that are within a given L2 distance from the ground truth as a low-level evaluation. We generate a cumulative mass function by adjusting the threshold between 0 and 150. We then compute the area under the curve (AuC) and normalize the outcome. Although it's vital to remember that our approach primarily concentrates on creating believable colorizations rather than just optimizing for pixel-level accuracy, this AuC metric offers a measure of raw prediction accuracy.  Our network performs better than our L2 variant (when trained from scratch) when trained on classification without rebalancing. When the L2 net is instead fine-tuned from a color classification network, it matches the performance of the classification network. This suggests that while the L2 metric can produce accurate colorizations, it is not very good at optimization from the beginning.

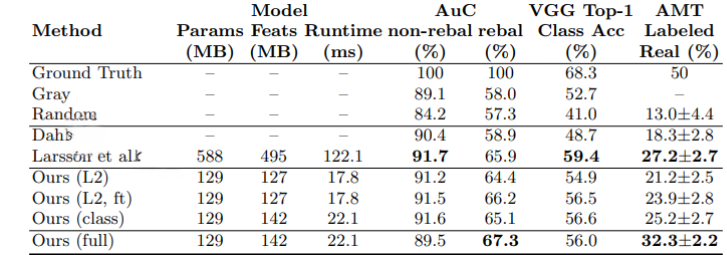
Fig 3. Comparison with other models

Fig 4. Model generated Results

References

[1] Cheng, Z., Yang, Q., Sheng, B. (2015). Deep colorization. In Proceedings of the IEEE International Conference on Computer Vision, 415–423. [2] J. Clerk Maxwell. A Treatise on Electricity and Magnetism, 3rd ed., vol.2. Oxford: Clarendon Press, 1892, pp. 68–73. [3] Deshpande, A., Rock, J., & Forsyth, D. (2015). Learning large-scale automatic image colorization. In Proceedings of the IEEE International Conference on Computer Vision, 567–575. [4] Richard Zhang, Phillip Isola, Alexei A. Efros, ”Colorful Image Colorization,” European Conference on Computer Vision (ECCV), 2016. [5] Weichen Pai. ”Image Colorization: Bringing Black and White to Life.” Medium, https://medium.com/@weichenpai/image-colorization- bringing-black-and-white-to-life-b14d3e0db763. Apr 7, 2024 [6] S. Anwar et al., ”Image Colorization: A Survey and Dataset,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 5, pp. 1134-1149, 2020. [7] I. Zeger et al., ”Grayscale Image Colorization Methods: Overview and Evaluation,” IEEE Transactions on Image Pro- cessing, vol. 30, no. 7, pp. 2042-2057, 2021. [8] A. Sousa et al., ”Automatic Colorization of Grayscale Images,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 3, pp. 587-599, 2021. [9] Q. Luan et al., ”Natural Image Colorization,” IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018. [10] W. Su et al., ”Instance-aware Image Colorization,” Conference on Computer Vision and Pattern Recognition (CVPR), 2020. [11] Larsson, G., Maire, M., Shakhnarovich, G.: Learning representations for automatic colorization. European Conference on Computer Vision (2016) [12] Iizuka, S., Simo-Serra, E., Ishikawa, H.: Let there be Color!: Joint End- to-end Learning of Global and Local Image Priors for Automatic Image Colorization with Simultaneous Classification. ACM Transactions on Graphics (Proc. of SIGGRAPH)(2016)

Copyright

Copyright © 2024 Shivang Kumar Singh, Anant Raj, Keshav Kumar, Darshan Kaur. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.