Image Compression Using Huffman and Shannon-Fano Coding: Performance Evaluation

Abstract

This paper studies Shannon-Fano coding versus Huffman coding as both are lossless compression techniques that bring out the difference in encoding symbols and performance. Shannon-Fano coding is simple but structured in method yet usually yields much worse compression. On the other hand, Huffman coding assigns code lengths based on symbol frequencies. As a result, Huffman coding yields higher compression ratios than Shannon-Fano coding. In this paper, we took a sample image and compressed its size using both Huffman and Shannon-Fano coding algorithms, and as a result, the image was compressed. Regarding compression, Huffman coding is more effective than Shannon-Fano coding since the output is observed to have a greater efficiency and the resulting file size is significantly less when compared to Shannon-Fano Coding.

Introduction

I. INTRODUCTION

Against this background, the explosion of multimedia content, especially images and videos, has created an enormous demand for efficient data storage and transmission. This led to the complete development of this technology often referred to as data compression, image compression, and encryption whereby the size of files can be reduced without lowering the quality of the data [7]. In particular, image compression plays a direct role in reducing the size of the file required for images so that images are transmitted quickly over networks and stored efficiently in memory-constrained environments. Also, the images can be compressed with the help of algorithms like DWT and fractal algorithms [11].

The compression techniques include lossy and lossless methods. Data compression by lossy methods involves compression with an allowance for some data loss, hence achieving greater compression ratios compared with lossless methods. Lossless methods maintain the original data integrity with no information loss through compression. The best-known lossless techniques are Shannon-Fano coding and Huffman coding, which represent symbols using variable-length prefix codes in such a way that the average number of bits used per symbol is minimized [8].

Shannon-Fano coding is another very early technique initially developed by Claude Shannon and Robert Fano in constructing codes based on the probability of occurrence of each symbol. It recursively divides the set of symbols into two parts with approximately equal total probabilities and assigns binary codes to both parts. However, although effective, this also does not always yield the best possible compression [10].

In this paper, we explore and compare Shannon-Fano and Huffman coding regarding an image compression process. The main objective is to judge the compression ratio, efficiency, and performance of each algorithm applied to digital images so that we finally show that Huffman's code provides superior compression than Shannon-Fano's code. This comparison is extremely important because it demonstrates how the choice of compression algorithm can largely impact stored space and transmission times for data-for example, while web browsing, archiving images, or real-time video streaming.

II. RELATED WORK & TECHNIQUE

Huffman coding is a popular lossless compression technique that plays a vital role in image compression algorithms. Here are some related works that we found after reading some papers and journals:

1) Classical use of Huffman Coding in an Image Compression

Huffman coding is utilized in larger image compression algorithms, notably JPEG compression. In JPEG, the DCT is used to convert the spatial domain data into frequency domain coefficients. After these coefficients are quantized, data is compressed using Huffman coding, which eliminates unnecessary information from the entropy encoding procedure. This method effectively shrinks the size of the entire image file [1].

2) Optimized Huffman Coding for Specific Image Types

There have been several adaptive Huffman coding techniques researched in this direction, aiming to improve the compression efficiency for specific types of images, be it medical images (such as CT scans and MRI) or satellite imagery. These optimizations focus on exploiting some characteristics of the content, such as some frequent occurrences of a certain number of pixel intensities, for better compression than traditional Huffman coding [2].

3) Combining Huffman Coding with other Comparison Algorithms

Huffman coding is often combined with other algorithms such as Run-Length Encoding (RLE), Lempel-Ziv-Welch (LZW), or Arithmetic coding to enhance the compression ratio. In our research paper, we combined the Huffman Coding algorithm with the Shannon-Fano algorithm to determine the better compressing algorithm for an image. Some research explores hybrid techniques to compress images more effectively. For example, Huffman coding may be used for entropy coding after transforming and quantizing an image via wavelet or fractal-based transformations [3].

4) Hybrid Huffman and Shannon-Fano Coding in Image Compression

A common approach is to use both algorithms for certain parts of the image. For example, Huffman coding can be applied to the most frequently occurring symbols while Shannon-Fano to the least frequently occurring ones to diminish the computational burden at the cost of compression ratio. In hybrid approaches, a division of labor between the two is very often based on the statistical characteristics of the image, e.g., frequency distribution [4].

5) Comparative Studies in Real-Time Image Processing

Hybrid Huffman and Shannon-Fano coding techniques are also applied in real-time image processing applications, such as live video streaming or remote sensing, where quick yet efficient compression is necessary. These comparative studies show that while Huffman coding alone provides the best compression, hybrid techniques reduce processing time without sacrificing much compression quality [5].

6) Parallel and Distributed Approaches

The work briefly speaks in parallel to hybrid Huffman-Shannon-Fano algorithm implementations that can compress high-resolution image data. Hybrid techniques make use of distributing the approach among several processors or threads to process lots of data in real-time. This hybrid approach, enables an initial fast estimation of coding trees with Shannon-Fano and then the critical section in the image follows with an optimized Huffman coding pass [6].

7) Improved Huffman Coding for Compression with Encryption

Huffman coding has been combined with some encryption algorithms to allow the safe transmission of images. Such methods first compress the images to be stored or transmitted through Huffman coding as a form of pre-compression. Then, compression of the images by algorithms such as AES or DES allows for security in storage and transmission; hence, Huffman coding is useful mainly with sensitive images such as medical or military imagery [7].

A. Huffman Coding Algorithm

Huffman Coding is a lossless data compression algorithm. The input characters are assigned variable-length codes by this technique. The lengths of assigned codes depend upon the frequencies of corresponding characters.

Since the assigned codes to the input characters are of variable length, hence these are known as prefix codes, which means that the codes assigned (bit sequences) are such that the code assigned to one character is not the prefix of code assigned to any other character. Thus, Huffman coding ensures that there is no confusion at the time of decoding the generated bit stream.

Let us understand prefix codes with a counter-example. Let there be four characters a, b, c, and d, and their corresponding variable length codes be 00, 01, 0, and 1. This coding results in ambiguity as the code assigned to c is the prefix of codes assigned to a and b. If the compressed bit stream is 0001, the de-compressed output may be "cccd" or "ccb" or "acd" or "ab". There are mainly two major parts in Huffman Coding

1. Build a Huffman Tree from input characters
2. Traverse the Huffman Tree and assign the codes to characters

Our Java program applies Huffman Coding to an image. The given image is a gray-scale or Colour image with pixel values according to the frequency at which they occur encoded. The program starts reading an image with the help of the class  Buffered Image` in Java's package `ImageIO`.

Then it starts processing the image by checking every pixel and getting its gray-scale value within the range between 0 and 255. These grayscale values are taken to generate a frequency map, with the key being the pixel value, and the value is the frequency (how many times that pixel value appears in the image).

With the frequency of each pixel value known, the code creates a Huffman Tree. In the Huffman Tree, each node represents a pixel value and the tree is constructed in such a way that the more frequently occurring values are closer to the root. The less frequent pixel values are further from the root. It achieves this using a priority queue (min-heap), which facilitates the merger of the lowest-appearing pixel value into a new parent node until all the pixel values are connected under one tree. The pixel values are now represented as a binary code obtained by tracing out their path in the tree: moving left appends a `0` to the code while moving right appends a `1`.

The Huffman Tree is then utilized by the program to generate binary codes for each pixel value. These are stored in a map called `Huffman codes`, which puts each pixel value against its corresponding Huffman code. Utilizing this map, the program compresses the image: each pixel is replaced by its corresponding binary Huffman code, which yields a long string of bits representing the whole image in compressed form. This compressed data can then be written to a file or transmitted for later decompression. In short, it compresses the storage size of this image in this code by encoding more frequently occurring pixel values using shorter binary codes and less frequently occurring pixel values using longer codes; thus, making the entire representation much more efficient overall.

B. Shannon-Fano Coding Algorithm

Shannon Fano Algorithm is one of the entropy encoding techniques used for the lossless data compression of multimedia. It is named after Claude Shannon and Robert Fano, which gives a code to each symbol based on the probability of occurrence of symbols. It is a variable-length encoding scheme, that is, the codes assigned to the symbols will be of varying lengths. In the Shannon-Fano Coding algorithm, we list out the probabilities or frequency counts of the given set of symbols so that the relative frequency of occurrence for each symbol is known.

Then, sort the following list of symbols in decreasing order of probability, from most probable to the left and least probable to the right. After that, we divide the list into two groups in such a manner that the sum of the probabilities becomes as close to one another as possible and assign 0 to the left-hand side and 1 to the right-hand side. We repeat the above 2 steps for each part until all the symbols are split into individual subgroups. In our Java program, we implemented a lossless image compression algorithm based on the Shannon-Fano coding technique. It begins with a definition of the `ShannonFanoNode` class, which wraps up each unique pixel value within a grayscale image, as well as its frequency of occurrence and the corresponding binary code assigned during compression.

This algorithmic core includes the following steps: first, the `calculateFrequency` method is the simple scan over the input image, and the counts of frequency for each pixel value at a range between 0 and 255 are noted. The gained frequency information is put in a map that will ease later computation. Then the code builds the list of `ShannonFanoNode` objects representing every pixel value with its frequency.

This generated list is then sorted in descending order based on the frequency to prioritize pixel values, which are the most frequently occurring in generating a code.

The recursive function, `generateShannonFanoCodes,` assigns the binary codes to the pixel values. This way it will divide the ordered list in two such that both lists have almost equal elements.

The '0' code will be assigned to the left list and '1' to the right list. This recursion will continue until all pixel values will have an assigned code. After this, the code develops a lookup map such that during compression, it will be able to instantly find the appropriate codes for the pixel values.

In the `main` method, the program reads a grayscale image from a file, calculates the pixel frequencies, generates corresponding Shannon-Fano codes, and compresses the image to the binary string representation. The compressed data resulting from this process, presented to standard output, shows how well the compression method works. This code is thus efficient in compressing a grayscale image while ensuring that the compressed data will perfectly reconstruct the original image.

III. FLOWCHARTS

A. Flowchart for Huffman Coding Algorithm

The flowchart for Huffman Coding algorithm is shown below –

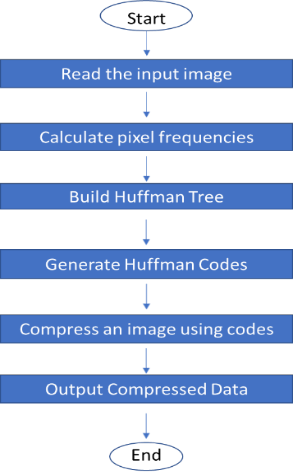
Fig A: Flowchart of Huffman Coding Algorithm for an Image Compression

B. Flowchart for Shannon-Fano Coding Algorithm

The flowchart for Shannon-Fano Coding algorithm is as follows:

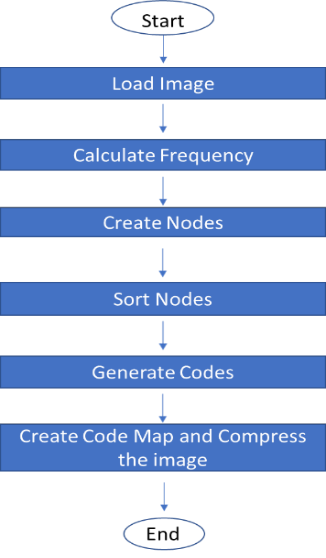
Fig B: Flowchart of Shannon-Fano Algorithm for an Image Compression

IV. RESULTS

At first, we took a sample image for compression. Before conversion, we noted some key parameters and original values of the parameters.

Fig C: Sample Image (Source: Internet)

1) Original Parameters

Fig D: Original image parameters

After Compression, we got different results for both the compression algorithms.

Fig E: Compressed image though Huffman Coding Algorithm

Fig F: Parameters of Compressed image through Huffman Coding Algorithm

Fig G: Compressed image though Shannon-Fano Coding Algorithm

Fig H: Parameters of Compressed image through Huffman Coding Algorithm

As you see in the above results the size of the image is getting reduced in both the algorithms, but in the case of the Huffman Coding Algorithm the size of the image is compressed more and the quality of the image is not much degraded. But as compared to the Shannon-Fano Algorithm, it also compresses the image but the quality of an image is degraded.

Conclusion

In general, Huffman coding generates more efficient encodings than Shannon-Fano. It typically results in shorter average code lengths, especially when symbols have greatly differing frequencies. Shannon-Fano coding is much easier to understand and implement. It is simply much less complicated in terms of code generation as compared with Huffman coding. Occasionally it generates longer average code lengths than Huffman coding. Huffman Coding Huffman Code is generally the choice for efficiency and optimality, where compression ratios are a matter of importance, like file compression, image formats, including JPEG, and video compression. Shannon-Fano Coding Shannon-Fano coding is found useful in simpler applications or for instructional purposes if the ease of implementation is an issue. Therefore, if you would want compression performance of the best type, then Huffman coding should be chosen. However, if one needs something just to illustrate the basic concept or just for very simple applications, then Shannon-Fano may be sufficient. We can conclude that the Huffman Algorithm compresses the image on a larger scale but it degrades the quality of the image while the Shannon-Fano Algorithm compresses the image at a smaller level while the quality of the image is better than that of the image compressed by the Huffman Algorithm.

References

[1] Wallace, G.K., 1992. The JPEG still picture compression standard. IEEE transactions on consumer electronics, 38(1), pp.xviii-xxxiv. [2] Kaur, I., and Sharma, K. \"Image compression using Huffman coding technique.\" International Journal of Advanced Research in Computer Science and Software Engineering 3.8 (2013): 517-523. [3] Anand, K. \"Huffman coding in digital image compression.\" International Journal of Engineering Research & Technology 2.4 (2013): 327-332. [4] Sukanya, B., and Sheela, K. P. \"A hybrid image compression scheme based on Huffman and Shannon-Fano coding.\" International Journal of Image Processing (IJIP) 6.4 (2012): 257-265. [5] Patil, D., and Deshmukh, M. \"Comparative study of real-time image compression using hybrid Huffman-Shannon-Fano coding in video streaming.\" International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering 4.2 (2015): 104-110. [6] Kumari, B., and Gupta, A. \"Parallel image compression using hybrid Shannon-Fano and Huffman coding.\" International Journal of Computer Applications 68.24 (2013): 10-15. [7] Sun, H., and Sun, B. \"Image encryption and compression based on Huffman coding.\" Journal of Physics: Conference Series 1449.1 (2020): 012034. [8] Muller, Rikus. “A study of image compression techniques, with specific focus on weighted finite automata.” (2005). [9] BENUSI, A., MARTIRI, E. and BAXHAKU, A., 2012. Huffman encoding for data content in the Albanian language used in image Steganography. International Journal of Science, Innovation & New Technology [10] Patel, R., Kumar, V., Tyagi, V. and Asthana, V., 2016, March. A fast and improved Image Compression technique using Huffman coding. In 2016 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET) (pp. 2283-2286). IEEE. [11] Jasmi, R.P., Perumal, B. and Rajasekaran, M.P., 2015, January. Comparison of image compression techniques using huffman coding, DWT and fractal algorithm. In 2015 International Conference on Computer Communication and Informatics (ICCCI) (pp. 1-5). IEEE. [12] Rufai, A.M., Anbarjafari, G. and Demirel, H., 2013, April. Lossy medical image compression using Huffman coding and singular value decomposition. In 2013 21st Signal processing and communications applications conference (SIU) (pp. 1-4). IEEE. [13] Fathahillah, F., Zain, S.G. and Rismawati, R., 2019. Homogeneous Image Compression Techniques with the Shannon-Fano Algorithm. International Journal of Environment, Engineering and Education, 1(2), pp.59-66. [14] Walidaniy, W.D., Yuliana, M. and Briantoro, H., 2022, August. Improvement of PSNR by Using Shannon-Fano Compression Technique in AES-LSB StegoCrypto. In 2022 International Electronics Symposium (IES) (pp. 285-290). IEEE. [15] Mantoro, T., Ayu, M.A. and Anggraini, Y., 2017, November. The performance of text file compression using Shannon-Fano and Huffman on small mobile devices. In 2017 International Conference on Computing, Engineering, and Design (ICCED) (pp. 1-5). IEEE.

Copyright

Copyright © 2024 Nihar Patil, Sachin Kapse, Aarya Shinde, Vishal Hange, Prof. Dipti Pandit. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.