Markov Chains for User Queries Mining: Image Retrieval Application using Internet

Abstract

We suggest a brand-new technique for automatically annotating, indexing, and retrieving photos based on annotations. We introduce the novel technique, which we term Markovian Semantic Indexing (MSI), within the framework of an image retrieval system in online mode. In the event that such a system exists, the queries entered by the users are utilised to build an Aggregate Markov Chain (AMC), which defines the significance between the terms the system sees. The photographs are automatically annotated based on the queries entered by the users. Next, depending on the annotation of each image and the keyword relevance recorded in the AMC, a stochastic distance between them is presented. The suggested distance is given geometric meanings, and its relationship to a grouping in the keyword space is examined. The optimality qualities of the suggested distance are demonstrated by the use of a novel Markovian state similarity measure, the mean first cross passage time (CPT). Images are represented as points in a vector space, and MSI is used to calculate how similar two images are. In Annotation-Based Image Retrieval (ABIR) tasks, it is demonstrated that the novel method outperforms Latent Semantic Indexing (LSI) and probabilistic Latent Semantic Indexing (pLSI) methods in terms of Precision against Recall and has some theoretical advantages.

Introduction

I. INTRODUCTION

The relationship between low-level features and high-level semantics of image content is lost in current computer vision algorithms, despite the fact that humans tend to identify images with high-level concepts. In general, there is no clear semantic meaning associated with either a single low-level feature or a combination of several low-level traits. Furthermore, the similarity measures among visual features do not always correspond with human perception, which leads to usually unsatisfactory and frequently unpredictable retrieval outcomes for low-level techniques. The lack of agreement between the information that may be inferred from visual data and the meaning that the same facts have for a user in a particular circumstance is known as the "semantic gap." The sensory gap, or the difference between an object in the real world and the data in a (computational) description attached to a recording of that thing, is another reason why the retrieval process fails. The first gap deals with how consumers interpret images and how hard it is to capture them in visual material; the second gap limits the ability to record and describe images, making it difficult to recognise content from them. As of right now, barely 10% of image files available online have a formal description (annotation). Because of this, picture search engines can only provide recall and precision of about 12% and 42%, respectively, and 60% of users use two or more search engines because they are dissatisfied with the results they get. The most frequent grievance is that semantics in content are not recognised by search engines. Furthermore, 77 percent of searchers switch up their terms multiple times due to an inability to find relevant material. The goal of Annotation-Based Image Retrieval (ABIR) systems is to integrate semantic content into image captions and text-based queries (e.g., Google Image Search, Yahoo! Image Search) more effectively. In order to find a more trustworthy idea association, the Latent Semantic Indexing (LSI)-based techniques, which were first used with more success in document indexing and retrieval, were integrated into the ABIR systems. Nevertheless, the degree of success of these endeavours is debatable; one explanation for this is the sparsity of the keyword annotation data per-image relative to the total number of keywords often supplied to documents. We provide a novel approach to automatic annotation and annotation-based image retrieval: Markovian Semantic Indexing (MSI). Due to its characteristics, MSI is especially well suited for ABIR assignments where there is a dearth of annotation data for each image. The method's features also make it especially useful in the context of online picture retrieval systems. The remainder of the document is structured as follows: We first introduce related work and our contribution in the following section. In Section 3, a proximity measure (distance) and the suggested methodology (MSI) are described. Section 4 looks at the ideal characteristics and geometric interpretation of the suggested distance. In Section 5, two well-known techniques from the literature, LSI and pLSI, are experimentally compared to MSI in two different scenarios:

a. Of supervised MSI annotation

b. Of external annotations realized with unknown methods.

This section also covers scalability considerations and a conceptual comparison of the methods. Section 6 contains the Conclusion. In this work, standard letters are scalars, bold letters are vectors, and capital letters are matrices. A bold letter with a subscript indicates a column vector; the subscript indicates where the letter belongs in a matrix. All vectors are regarded as column vectors unless specifically stated otherwise, with the exception of equilibrium vectors, which are typically regarded as row vectors.

II. RELATED WORK AND OUR CONTRIBUTION

Without a doubt, content-based retrieval has grown quickly. Over 200 content-based retrieval systems have been created recently, most of them relying on low-level features. Specifically, they fall into two primary categories:

1. People who carry out semantic mining by examining textual data related to images, including captions, annotations, keywords allocated to the images, alternative (alt) text on HTML sites, and surrounding text,
2. Systems that use low-level visual properties like colour and texture to extract them in order to perform various tasks on image data, like alignment, categorization, browsing, searching, and summarising.

The latter methods typically aren't able to capture semantics effectively, while the methods in the first category rely heavily on tedious annotation. Furthermore, some other methods accomplish content-based operations by using both low-level features—visual keywords and text annotation—but they typically require users' conscious participation in order to annotate photographs linguistically. More effective semantic material is incorporated into both text-based queries and image captions by Annotation-Based Image Retrieval systems. As a direct result, techniques originally created for document retrieval might also work well for ABIR systems. Originally, Latent Semantic Indexing was created for document retrieval.

Hofmann developed probabilistic Latent Semantic Indexing (pLSI), which is based on the Aspect Model and offers a document retrieval alternative to projection (LSI) or clustering techniques. In order to overcome the generalisation and overfitting issues with pLSI, Latent Dirichlet Allocation (LDA) was introduced by Bleiet al. Griffiths and Steyvers then combined LDA with a Markov chain Monte Carlo approach. In order to address overfitting issues, Steyvers et al. developed a novel probabilistic model for document retrieval that included Gibbs sampling to represent both authors and themes. There have been attempts to use LSI/pLSI-based methods to find a more trustworthy idea connection in ABIR systems. Joint models across text and images have already been investigated in the computer vision literature. Based on the aspect model as well, Barnard and Forsyth presented a statistical model with hybrid text/visual features. Li et al. developed a different model based on Bayesian incremental learning, and Fan et al. suggest a multilevel automatic annotation method based on both local and global visual data. Although stochastic in nature, the method shown here elevates the reasoning component of probability by clearly defining the relevance relationships between keywords. In AI systems, it is common practice to capture semantics via network representations. These are known as galleries, qualitative Markov networks, or constraint networks in the Dempster-Shafer theory; they are also known as influence diagrams, causal nets, or Bayesian networks in probability theory. It has been demonstrated that associational graphs—such as semantic networks, constraint networks, inference networks, conceptual dependencies, and conceptual structures—better capture the plausibility of human reasoning in many models of human reasoning.

A. Our Contribution

This paper proposes a novel (alternative) probabilistic strategy for Annotation Based picture Retrieval that is more appropriate for sparsely annotated domains (e.g., picture databases) where the per image sparse keyword annotation is constrained, than LSI and pLSI. It tackles the zero frequency problem more naturally, which is the idea that there is usually little chance of finding similar keywords even in closely related photos because the images are not annotated with exactly the same phrases. Here, an explicit relevance link between terms with a probabilistic weight is used to solve this issue. The approach's main idea is to use a probabilistic qualitative reasoning annotation technique to convey partial views about the links between keywords, making up for the scant data. Thus, a mechanism that improves performance by mining the structure of the available data is introduced instead of adding additional data, as is the case with standard models. Moreover, the suggested system is unique in the manner it combines these two tasks, even though automatic annotation and annotation-based image retrieval systems have been published in the literature. In order to dynamically mine semantics towards qualitative probabilistic reasoning, it is envisaged that both the automatic annotation and retrieval activities will take place in the implicit user interaction context. It is demonstrated that MSI is ideal in relation to CPT. Conceptual comparisons between pLSI and LSI as well as between the two show benefits for the suggested method.

III. THE PROPOSED APPROACH

By providing photos that are more likely to be accepted (downloaded) by the user, the goal is to increase user happiness. It is assumed that users ask questions in order to look for photos, and each question consists of an ordered list of keywords. In response, the system displays a list of pictures. The user has the option to download the returned images or to disregard them and submit a new query. The system considers the photos unannotated throughout the training phase. The system automatically annotates the photos as users select images and pose queries. It also creates relevant associations between the keywords, as will be detailed later in the article. The system annotates the photographs invisibly from the user; the user never explicitly does this. In order to return images that more accurately reflect the user's preferences and increase user satisfaction, the system utilises both the annotations that were made available during the training phase and the keyword relevance probability weights that were also assessed during that phase. We use the implicit effects of this interactive process one by one as we build the suggested system step-by-step:

Step 1: The user implicitly relates the retrieved (downloaded) images to her/his query. By assuming Markovian chain transitions in the order of the keywords the aim of the proposed approach is to quantify logical connections between keywords. If some user relates image Ii to his query qi , where keyword k2 follows keyword k1 and this occurs m times, then the one step transition probability pi(k1,k2) is being updated as follows: if pi(k1,k2) is the current probability (before the update) based on M keywords then the new probability (based on M + m keywords) is calculated by the recurrent formula

Using this process, a Markov chain is created, with each keyword representing a state. A keyword's state counter advances each time it occurs in a query, and its interstate link counter advances if another keyword appears in the same query after it. This method is used to measure both the frequency of the keywords and their order of occurrence. Batch processing of the image-related queries results in the advancement of the counters and the updating of the probabilities as previously said. The counts are cleared before to processing the subsequent batch of requests. For every image Ii, the equilibrium state vector of the so-constructed Markov Chain will be represented by πi, which will now stand in for the image.

This modelling technique is supported by two factors: 1) the conceptual approach used in this work is qualitative; and 2) the MSI's targeting characteristics, which aim to capture aspects unique to each user, such as perception of visuals. In fact, the assignment of a logical connection of relevance between these two keywords, in addition to the individual connections between each keyword and the selected image, is justified by the fact that each sequence of keywords (query) originates from a specific user, filtered through her/his perception about the selected image. Our modelling approach favours this logical relationship over the conventional numerical method of estimating the distribution of images over keywords.

Step 2: One encounters the zero-frequency issue when attempting to compare the probability vectors πi and πj for the two images that were computed in the previous step directly. The very act of a user combining specific phrases in a query implicitly positions the keywords in relation to one another, independent of the specific images the user may or may not choose. By grouping related keywords together, we suggest using this to solve the zero-frequency issue. This stage creates the Aggregate Markovian Chain (AMC) of all user inquiries, regardless of the photos they have selected, for this reason. The kernel of this process denoted by PG, is calculated in a similar to the previous step manner by the recurrent formula of (1).

The aim of the AMC is to model keyword relevance since, although PG uses a Markov kernel, it will be utilised to cluster the keyword space rather than estimate an explicit probability distribution.

Step 3: Step of optimisation. The keyword space will be clustered using the AMC, and through this clustering, explicit relevance linkages between the keywords will be defined. By assessing the series FG(n)= ∑_(k=0)^n PkG, where PG is the AMC kernel, the clustering job is connected to the convergence properties of the AMC chain. Not before the rapid convergence has completed, but at the desired n where the slow convergence has taken over, is where an appropriate termination condition puts an end to the series. Since the clusters in the rows of FG(n) will lose rank and the determinant will approach zero, the value of the determinant of FG(n) is employed as a termination condition. The n-step predicted occupancies matrix is denoted by FG(n) (Appendix). This process is associated with an optimisation problem concerning the total variance of the columns of FG(n), when projected in the direction of the PG eigenvectors. We shall learn more about this idea in the following section. ?(1/(n+1)) FG(n), the n-step predicted fractional occupancies matrix (Appendix), computed at the desired n, shall now be noted using only FG.

Step 4: At this point, the MSI distance's formal definition can be given. Definition 1. Let x and y be two pictures, denoted by the corresponding row vectors of their steady state probabilities, x and y. Let furthermore ∑(FGT) be the covariance matrix of the Aggregate Markov Chain (AMC) zero-mean transpose anticipated fractional occupancies matrix, computed at the chosen n. Next, we define the MSI distance between image x and image y as              

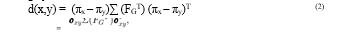
where the corresponding coordinates have been filled in with zeros to increase the dimensionality of πx and πy to that of ∑(FGT). Since the suggested distance is a generalised Euclidean distance function utilising a covariance matrix that is always positive definite, it is well defined.

IV. GEOMETRIC INTERPRETATION AND OPTIMALITY PROPERTIES OF THE MSI DISTANCE

When projected on the direction of the difference, (πx - πy), between the two pictures, the proposed MSI distance d(x,y) (Definition 1) can be seen as measuring the total variance of the rows of FGT. The direction determined by the vector difference of the probability distributions of the two specific images is actually determining the distance between them because the FGT is only calculated once from all the data. Understanding the mechanics of the Markovian convergence that generates the FGT and its relationship to certain directions in the keyword space is necessary to obtain further geometric and stochastic interpretations of the MSI distance. We will explore the geometric interpretation of the convergence process and how it relates to the suggested distance in terms of state clusters and state connection metrics in the remaining portion of this section. We will make use of standard language, concepts, and notation found in the literature on stochastic processes. For a concise overview, please refer to the Appendix.

A. The Eigenvector Convergence Process of the Markov Kernel as a Foundation for State Partition

This section explains how the convergence of an initial condition to its corresponding equilibrium state occurs along the eigenvectors of the Markov kernel, with each direction's relative rate of convergence determined by its corresponding eigenvalue. For a brief introduction to the notation of Ti(n), ti(n), and tg(i) and their values Tij(n), tij(n), respectively, as well as other pertinent terms utilised below, the reader is referred to the Appendix. Since the chain converges with rate 1 in this direction, as will be shown later in this section, the equilibrium state for the corresponding initial condition is the l1 normalised eigenvector, which corresponds to an eigenvalue of 1.

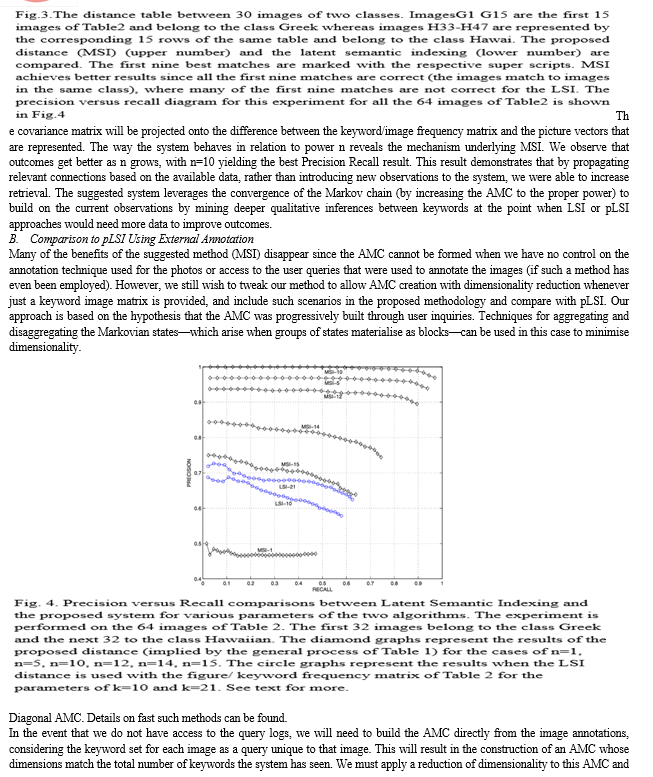
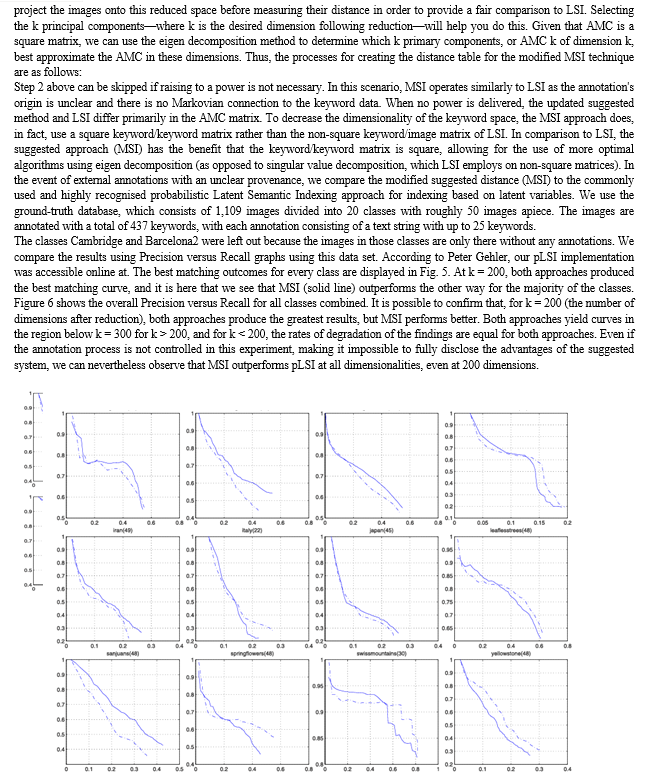
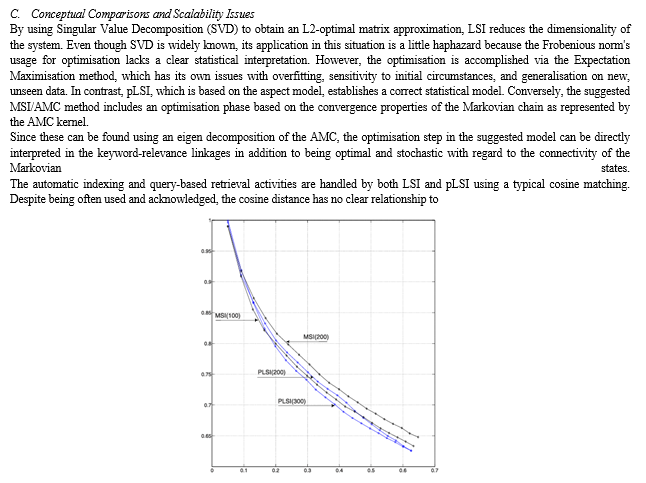
Conclusion

By characterising keyword importance as a connection measure between Markovian states that are modelled after user queries, we introduced the Markovian Semantic Indexing, a novel approach to mining user queries. The queries of the same consumers who would be serviced by the proposed system are used to dynamically train it. As a result, targeting is more precise than in other systems that define keyword relevance through external, non-dynamic, or non-adaptive methods. Using an Aggregate Markovian Chain, a stochastic distance was created in the form of a generalised euclidean distance, and it turned out to be optimal with regard to specific Markovian connectivity measures that were designed specifically for this purpose. A theoretical comparison between the suggested method (MSI) and Latent Semantic Indexing and Probabilistic Latent Semantic Indexing indicated several advantages. Studies have demonstrated that MSI performs better when retrieving information from poorly annotated picture data sets. When 64 photos were collected from Google Image Search and transparently annotated using the suggested system, the results showed that the MSI method had certain advantages over LSI, primarily in terms of collecting images with more complex connections than just keyword cooccurrence. After adapting the suggested approach to include AMC creation and dimensionality reduction in external annotations, a second comparison to pLSI was carried out using the ground-truth annotated collection of 1,109 images. For this experiment, the Precision versus Recall findings showed that MSI outperforms pLSI in all dimensionalities up to 200 dimensions.

References

[1] S. Santini and R. Jain, “Similarity Measures,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 21, no. 9, pp. 871-883, Sept. 1999. [2] K. Stevenson and C. Leung, “Comparative Evaluation of Web Image Search Engines for Multimedia Applications,” Proc. IEEE Int’l Conf. Multimedia and Expo, July 2005. [3] comScore’s Report Article, “Comscore’s Qsearch 2.0 Service,” comScore’s Report Article, www.comscore.com, 2007. [4] B.J. Jansen, A. Spink, and T. Saracevic, “Real Life, Real Users, and Real Needs: A Study and Analysis of User Queries on the Web,” Information Processing and Management, vol. 36, no. 2, pp. 207-227, 2000. [5] R. Datta, D. Joshi, J. Li, and J.Z. Wang, “Image Retrieval: Ideas, Influences, and Trends of the New Age,” ACM Computing Surveys, vol. 40, no. 2, pp. 1-60, 2008. [6] A. Bhattacharya, V. Ljosa, J.-Y. Pan, M.R. Verardo, H. Yang, C. Faloutsos, and A.K. Singh, “Vivo: Visual Vocabulary Construction for Mining Biomedical Images,” Proc. IEEE Fifth Int’l Conf. Data Mining, Nov. 2005. [7] J. Li and J. Wang, “Real-Time Computerized Annotation of Pictures,” Proc. ACM 14th Ann. Int’l Conf. Multimedia, 2006. [8] D. Joshi, J.Z. Wang, and J. Li, “The Story Picturing Engine - A System for Automatic Text Illustration,” ACM Trans. Multimedia Computing, Comm. and Applications, vol. 2, no. 1, pp. 68-89, 2006. [9] M.W. Berry, S.T. Dumais, and G.W. O’Brien, “Using Linear Algebra for Intelligent Information Retrieval,” SIAM Rev., vol. 37, no. 4, pp. 573-595, 1995. [10] T. Hofmann, “Probabilistic Latent Semantic Indexing,” Proc. 22nd Int’l Conf. Research and Development in Information Retrieval (SIGIR ’99), 1999. [11] T. Hofmann, “Unsupervised Learning by Probabilistic Latent Semantic Analysis,” Machine Learning, vol. 42, no. 1/2, pp. 177- 196, 2001. [12] D.M. Blei and A.Y. Ng, and M.I. Jordan, “Latent Dirichlet Allocation,” J. Machine Learning Research, vol. 3, pp. 993-1022, 2003. [13] T.L. Griffiths and M. Steyvers, “Finding Scientific Topics,” Proc. Nat’l Academy of Sciences USA, vol. 101, no. suppl. 1, pp. 5228-5235, 2004. [14] M. Steyvers, P. Smyth, M. Rosen-Zvi, and T. Griffiths, “Probabilistic Author-Topic Models for Information Discovery,” Proc. 10th ACM SIGKDD Conf. Knowledge Discovery and Data Mining, 2004. [15] Z. Guo, S. Zhu, Y. Chi, Z. Zhang, and Y. Gong, “A Latent Topic Model for Linked Documents,” Proc. 32nd Int’l ACM SIGIR Conf. Research and Development in Information Retrieval (SIGIR), 2009. [16] T.-T. Pham, N.E. Maillot, J.-H. Lim, and J.-P. Chevallet, “Latent Semantic Fusion Model for Image Retrieval and Annotation,” Proc. 16th ACM Conf. Information and Knowledge Management (CIKM), 2007. [17] R. Datta, D. Joshi, J. Li, and J.Z. Wang, “Image Retrieval: Ideas, Influences, and Trends of the New Age,” ACM Computing Surveys, vol. 40, no. 2, article 5, pp. 1-60, 2008. [18] F. Monay and D. Gatica-Perez, “On Image Auto-Annotation with Latent Space Models,” Proc. ACM Int’l Conf. Multimedia (MM), 2003. [19] K. Barnard and D. Forsyth, “Learning the Semantics of Words and Pictures,” Proc. Int’l Conf. Computer Vision, vol. 2, pp. 408-415, 2001. [20] L.-J. Li and G. Wang, and L. Fei-Fei, “OPTIMOL: Automatic Online Picture Collection via Incremental Model Learning,” Int’l J. Computer Vision, vol. 88, no. 2, pp. 147-168, 2010. [21] J. Fan and Y. Gao, and H. Luo, “Integrating Concept Ontology and Multitask Learning to Achieve More Effective Classier Training for Multilevel Image Annotation,” IEEE Trans. Image Processing, vol. 17, no. 3, pp. 407-426, Mar. 2008. [22] G. Shafer, P.P. Shenoy, and K. Mellouli, “Propagating belief Functions in Qualitative Markov Trees,” Int’l J. Approximate Reasoning 1, vol. 4, pp. 394-400, 1987. [23] L.G. Shapiro, “GroundTruth Database,” http://www.cs. washington.edu/research/imagedatabase/groundtruth/, Univ. of Washington, 2012. [24] J. Pearl, Probabilistic Reasoning in Intelligent Systems. Morgan Kaufmann, 1988. [25] L.D. Lowrance, T.D. Garvey, and T.M. Strat, “A Framework for Evidential Reasoning Systems,” Proc. Fifth Nat’l Conf. Artificial Intelligence (AAAI ’86), pp. 896-901, 1986. [26] U. Montanari, “Networks of Constraints, Fundamental Properties and Applications to Picture Processing,” Information Science, vol. 7, pp. 95-132, 1974. [27] W. Woods, Representation and Understanding, D. Bobrow and A. Collins, eds. Academic Press, 1975. [28] R.O. Duda, P.E. Hart, and N.J. Nilsson, “Subjective Bayesian Methods for Rule-Based Inference Systems,” Proc. Nat’l Computer Conf. and Exposition (AFIPS), vol. 45, pp. 1075-1082, 1976. [29] R. Schank, “Conceptual Dependency: A Theory of Natural Language Understanding,” Cognitive Psychology, vol. 4, pp. 552- 631, 1972. [30] J.F. Sowa, Conceptual Structures: Information Processing in Mind and Machine. Addison-Wesley, 1984. [31] O. Tuzel, F. Porikli, and P. Meer, “Pedestrian Detection via Classification on Riemannian Manifolds,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 30, no. 10, pp. 1713-1727, Oct. 2008. [32] R. Howard, Dynamic Probabilistic Systems. John Wiley and Sons, Inc., 1971. [33] G. Zhen, Z. Shenghuo, C. Yun, Z. Zhongfei, and G. Yihong, “A Latent Topic Model for Linked Documents,” Proc. 32nd Int’l ACM SIGIR Conf. Research and Development in Information Retrieval (SIGIR ’09), 2009. [34] W.J. Stewart, Numerical Solution of Markov Chains. Princeton Univ. Press, 1994. [35] http://people.kyb.tuebingen.mpg.de/pgehler/code/index.html, 2012.

Copyright

Copyright © 2024 Dr. Madhav M. Bokare, Mr. Amol V. Suryawanshi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.