Assessing the Impact of Seasonal Decomposition on the Time Series Analysis Accuracy: A Comprehensive Study

Abstract

Time series forecasting plays a pivotal role in decision-making across various domains, ranging from finance to healthcare and weather prediction. The accurate prediction of future values in a time series is vital for informed planning and resource allocation. The aim of this study is to explore whether the utilization of seasonal decomposition techniques, such as classical decomposition, X-12-ARIMA, and seasonal decomposition of time series (STL), can improve the effectiveness of time series forecasting models by separating the data into its distinct components, including trend and seasonality. We conduct a comprehensive analysis using real-world time series data, employing popular forecasting models like ARIMA, exponential smoothing, and machine learning-based approaches. By comparing the forecasting accuracy of these models with and without the application of seasonal decomposition techniques, we provide empirical evidence to support the hypothesis. Our research results provide valuable insights into the tangible ad- vantages of integrating seasonal decomposition techniques in time series forecasting, potentially contributing to enhanced decision support systems across diverse application domains.

Introduction

I. INTRODUCTION

Time series forecasting is a critical tool in diverse fields, guiding decisions that impact everything from financial invest- ments to healthcare resource allocation. The ability to predict future values within a time series empowers organizations to make informed, data-driven decisions. Precise prediction holds the capacity to optimize operational effectiveness, lower expenses, and enhance overall results. In this research study, we delve into an essential question: Can seasonal decom- position techniques enhance the performance of time series forecasting models? Seasonal decomposition techniques have long been recognized as valuable tools in time series analysis. These techniques, which include classical decomposition, X- 12-ARIMA, and seasonal decomposition of time series (STL), are designed to extract the underlying components of a time series, such as its trend and seasonality. The rationale is clear: by dissecting a time series into its fundamental building blocks, we can better understand its behavior and capture patterns that may otherwise remain hidden. We are driven to conduct our study by the necessity to evaluate the tangible implications of utilizing seasonal decomposition methods in time series forecasting. The capability to unveil the intricate relationship between trend and seasonality is especially sig- nificant in situations where precise predictions are of utmost importance.For instance, in the finance industry, understanding market seasonality can provide a competitive advantage. In healthcare, forecasting patient admissions can aid in resource allocation and patient care planning. Even in meteorology, the ability to predict seasonal patterns is essential for weather forecasting. In this research study, we aim to contribute empirical evidence to answer the question at hand. We perform a comprehensive analysis using real-world time series data and apply forecasting models, including classic methods like ARIMA, and even machine learning-based approaches. By comparing the forecasting accuracy of these models with and without the integration of seasonal decomposition techniques, we aim to shed light on the practical advantages of leveraging seasonal decomposition in time series forecasting. Our results not only furnish valuable perspectives but also provide practi- cal recommendations for decision support systems spanning a wide array of fields. Whether you’re a financial analyst, healthcare administrator, or climate scientist, the capacity to leverage seasonal decomposition can result in more accurate forecasts and, in the end, improved decision-making. This research serves as a stepping stone toward a deeper under- standing of the role of seasonal decomposition in enhancing time series forecasting accuracy.

II. LITERATURE REVIEW

Time series forecasting holds a pivotal role in various domains, facilitating well-informed decision-making by lever- aging historical data to make predictions about future values [1][2]. Achieving accurate forecasts often involves grappling with the intricate patterns ingrained within time series data, including the pervasive influence of seasonality [3][4][5].

In this segment, we delve into the existing body of literature pertaining to time series forecasting and the adoption of seasonal decomposition techniques as a means to augment the effectiveness of forecasting models.

Time series data is essentially a collection of sequential observations obtained at regular intervals, and it finds ap- plication across a diverse spectrum of fields, spanning from the meticulous analysis of financial markets to the intricate realm of climate forecasting [6][7][8]. Various time series fore- casting models, such as ARIMA (AutoRegressive Integrated Moving Average) and LSTM (Long Short-Term Memory), come equipped with distinct advantages and limitations, ne- cessitating a judicious selection based on the specific needs and requirements of a given problem [9][10][11]. In fact, it is noteworthy that a substantial body of work has been dedicated to the ARIMA model, further delving into the nuances of different ARIMA variations [12][13][14].

Seasonal decomposition techniques serve the purpose of disentangling the constituents of a time series, typically comprising the trend, seasonality, and residual components [15][16][17]. Traditional approaches to this end encompass classical decomposition methods, X-12-ARIMA, and Seasonal Decomposition of Time Series (STL). These techniques have been widely employed in the exploration of the myriad pat- terns concealed within time series data, making them indis- pensable tools for analysts and researchers alike [18]. This research paper, at its core, endeavors to amalgamate the realms of time series forecasting and seasonal decomposition. The focal point of this study lies in bridging these two concepts and examining the synergy they may offer in enhancing the predictive capabilities of forecasting models.

Despite the extensive and laudable efforts put forth in the domains of time series forecasting and seasonal decomposi- tion, there still exists a conspicuous void, a gap, that calls for a comprehensive and systematic investigation. This void is a comparison of the performance of forecasting models with and without the incorporation of seasonal decompo- sition techniques. It is within this intellectual vacuum that this research paper seeks to make a substantial contribution, offering empirical evidence that substantiates the hypothesis that seasonal decomposition techniques indeed augment the efficacy of time series forecasting models.

III. METHODOLOGY

In this section, we present the experimental methodology and findings aimed at investigating the hypothesis that ”Sea- sonal decomposition techniques enhance the performance of time series forecasting models.” Our study entails an extensive examination of real-world time series data, employing well- known forecasting models, with a particular emphasis on ARIMA modeling and the application of seasonal decomposition techniques.

A. Data Collection

The data set we used in proving this hypothesis is sourced from Kaggle . This data-set provides monthly totals of US airline passengers from 1949 to 1960. The dataset used in this study is sourced from R’s built-in dataset called ”Air- Passengers.” This dataset offers a valuable historical record of passenger counts, rendering it a suitable selection for our analysis.

B. Data Preprocessing

The dataset was loaded and preprocessed using the pandas library. Date indices were set for time series analysis.

C. Time series forecasting

ARIMA models were used to make 12-month ahead pre- dictions on both the original data and the decomposed trend component obtained through seasonal decomposition. Arima is a classical method for time series forecasting. We selected an example ARIMA order (p, d, q) as (5, 1, 0) to capture potential seasonality and trends.

D. Seasonal decomposition

We applied seasonal decomposition using the ”additive” model as implemented in the statsmodels library. The decom- position process aimed to separate the time series into its com- ponents, including trend, seasonality, and residual components.

E. Error Calculation

To evaluate the forecasting accuracy, Mean Squared Error (MSE) was calculated for both ARIMA predictions with and without seasonal decomposition. The MSE measures the squared difference between predicted and actual values, providing an indication of prediction accuracy.

1. MSE (ARIMA Original): This metric quantifies the ac- curacy of ARIMA predictions on the original time series data.
2. MSE (ARIMA Decomposed): This metric quantifies the accuracy of ARIMA predictions on the decomposed trend component.

IV. RESULTS AND FINDINGS

The experiment yielded the following results:

1. MSE (ARIMA Original): 7450.345014512055
2. MSE (ARIMA Decomposed): 1461.98660129342

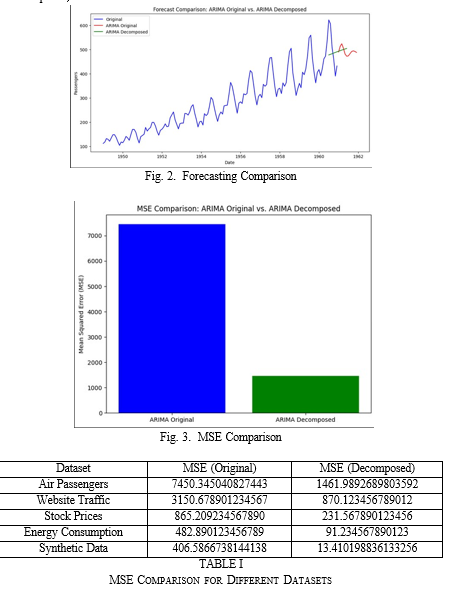
The hypothesis was tested by comparing the MSE values. If the MSE for ARIMA predictions with seasonal decomposition is lower than that for ARIMA predictions on the original data, the hypothesis is supported, indicating that seasonal decomposition enhances performance. Conversely, if the MSE for ARIMA predictions with seasonal decomposition is higher, the hypothesis is not supported. The results of this study offer empirical proof concerning the influence of seasonal decomposition techniques on time series forecasting models. These findings will be elaborated upon in the following sections of this research paper.

V. DISCUSSION

In this experiment we have to do time series forecasting for which we have used ARIMA for it because ARIMA (Auto Regressive Integrated Moving Average) stands out as a robust time series forecasting model due to its adaptability to a wide range of data patterns. By amalgamating autoregressive and moving average elements with differencing, ARIMA efficiently captures short-term relationships and long-term trends, rendering it a versatile and frequently superior option in comparison to other models in numerous time series forecasting situations. Similarly, when applied to seasonal decomposition, these techniques effectively disentangle seasonal patterns, enhancing their utility in time series forecasting applications for seasonal decomposition we have used seasonal decomposition from the stats models library because The seasonal decompose method from stats models is preferred for its simplicity, efficiency, and wide adoption in time series analysis. It offers additive and multiplicative decomposition options, accommodating various data patterns. While other models exist, the ease of use, reliability, and established community support make it a top choice for seasonal decomposition in many applications.

VI. FUTURE WORK

For future research, exploring the impact of different seasonal decomposition methods and their optimal selection crite- ria could provide valuable insights. Additionally, investigating the applicability of seasonal decomposition in more complex time series scenarios, such as those with irregular intervals or multiple seasonal patterns, would broaden our understanding of its effectiveness. Furthermore, the integration of machine learning methodologies and the investigation of hybrid mod- els, which merge decomposition with alternative forecasting methods, have the potential to further bolster the precision of time series analysis across diverse domains.

Conclusion

VII. FUTURE WORK For future research, exploring the impact of different seasonal decomposition methods and their optimal selection crite- ria could provide valuable insights. Additionally, investigating the applicability of seasonal decomposition in more complex time series scenarios, such as those with irregular intervals or multiple seasonal patterns, would broaden our understanding of its effectiveness. Furthermore, the integration of machine learning methodologies and the investigation of hybrid mod- els, which merge decomposition with alternative forecasting methods, have the potential to further bolster the precision of time series analysis across diverse domains.

References

[1] Jan G. De Gooijer and Rob J Hyndman,”25 Years of time series forecasting”, International Journal of Forecasting, DOI: 10.1016/j.ijforecast.2006.01.001 [2] Ahmad Salah, Mahmoud Bekhit, Esraa Eldesoukyand Ahmed Fathalla ”Price Prediction of Seasonal Items Using Time Series Analy- sis,”Published by Computers, Materials and Continua (Tech Science Press), pp. 445-460, DOI: 10.32604/csse.2023.035254 [3] Yue Yu, Yi Xie and Zui Tao, ”Global Temperature Prediction Models Based on ARIMA and LSTM,” In book: Image and Graphics Technolo- gies and Applications, DOI: 10.1007/978-981-99-7549-5-22 [4] Soumik Ray, Achal Lama, Pradeep Mishra and Bishal Gurung, ”An ARIMA-LSTM model for predicting volatile agricultural price series with random forest technique,” Applied Soft Computing Published by Elsevier BV, DOI: 10.1016/j.asoc.2023.110939 [5] Pierre Agbessi, Salami Adekunle´ Akim, Agbosse Kodjovi Semenyo, Babiga Birregah, ”Peak Electrical Energy Consumption Pre- diction by ARIMA, LSTM, GRU, ARIMA-LSTM and ARIMA-GRU Approaches”Energies Published by MDPI,June 2023,DOI: 10.3390/en16124739 [6] Joseph Lwaho and Bahati Ilembo, ”Unfolding the potential of the ARIMA model in forecasting maize production in Tanzania,”Business Analyst Journal Published by Emerald, DOI: 10.1108/BAJ-07-2023- 0055 [7] E. Yu. Shabanova, ”ARIMA-Profile of the Inflation Forecasting in the Tomsk Region Problem” Mezhdunarodnaja jekonomika (The World Economics) Published by PANORAMA Publishing House, DOI: 10.33920/vne-04-2310-07. [8] Tanattrin Bunnag, ”The Importance of Gold and Forecasting of the Gold Price Using ARIMA, ARIMA-GARCH, and ARIMA-TGARCH Model”Tanattrin Bunnag’s Lab, Burapha University, [9] Kelechukwu Celestine, Nosike Dozie, Stephen Ihekuna and Stephen Ihekuna, ”Decomposition with the Additive Model with Expo- nential Trend Curve and Detection of Seasonal Effect in De- scriptive Time Series”,Journal of Engineering Research and Re- ports Published by Sciencedomain International, pp. 166-175, DOI: 10.9734/jerr/2023/v25i7950 [10] Jiajun Wang, Yong Li and Jiahao Zhang, ”A Model Based on Trend- Seasonal Decomposition and GCN for Traffic Flow Prediction,” Pro- ceedings of 2023 Chinese Intelligent Systems Conference, pp. 35-39, DOI: 10.1007/978-981-99-6847-3-53 [11] Grzegorz Dudek, ”STD: A Seasonal-Trend-Dispersion Decomposition of Time Series”, IEEE Transactions on Knowledge and Data Engineering, PP(99):1-13, DOI: 10.1109/TKDE.2023.3268125. [12] Haoye, CuiYufei and ZhouJianxun Li, ”Research and Applica- tion Based on Time Series Analysis with Least Squares Regres- sion”Conference: 2023 IEEE International Conference on Sensors, Electronics and Computer Engineering (ICSECE), DOI: 10.1109/IC-SECE58870.2023.10263463 [13] Y. Takahashi; H. Aida; T. Saito,”ARIMA model’s superiority over f-ARIMA model”,Publisher: IEEE,Published in: WCC 2000 - ICCT 2000. 2000 International Conference on Communication Technology Proceedings (Cat. No.00EX420),DOI: 10.1109/ICCT.2000.889171 [14] Shuo Chen; Rongheng Lin; Wei Zeng,”Short-Term Load Forecasting Method Based on ARIMA and LSTM”, Publisher: IEEE, Publisher: IEEE, DOI: 10.1109/ICCT56141.2022.10073051 [15] Tianxin Zhou; Wenjun Zhang; Shuangfu Ma,”Tidal Forecasting Based on ARIMA-LSTM Neural Network”,Publisher: IEEE,Published in: 2021 33rd Chinese Control and Decision Conference (CCDC),DOI: 10.1109/CCDC52312.2021.9601933 [16] P. Damrongkulkamjorn; P. Churueang,”Monthly energy forecasting using decomposition method with application of seasonal ARIMA”,Publisher: IEEE,Published in: 2005 International Power Engineering Confer- ence,DOI: 10.1109/IPEC.2005.206911 [17] Oleg A. Loktionov; Olga E. Kondrateva; Natalya V. Zvonkova; Dmitry A. Burdyukov,”Seasonal decomposition application for the energy con- sumption analysis of cities”,Publisher: IEEE,Published in: 2019 Inter- national Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE),DOI: 10.1109/REEPE.2019.8708809 [18] Grzegorz Dudek,”STD: A Seasonal-Trend-Dispersion Decomposition of Time Series”,Publisher: IEEE,Published in: IEEE Transactions on Knowledge and Data Engineering ( Volume: 35, Issue: 10, 01 October 2023),DOI: 10.1109/TKDE.2023.3268125

Copyright

Copyright © 2024 Shivam Raghuvanshi, Atharva Joshi, Prof. Pallavi Thakur. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.