Impact of Thermal Forces on Curved Bridge Bearings: A Comparative Study of Rigid and Elastic Link Configurations According to ASC Code Standards

Abstract

For any bridge, the bearings are arranged such that the internal forces due to thermal, creep and shrinkage effects can be minimized in the deck. A typical bearing arrangement for the straight bridges, releasing all the constrained internal forces from the deck. The arrangement helps in the simplification and optimization of the deck design calculations. It is important to note that the expansion joints at the ends A and C shall accommodate the longitudinal displacements due to thermal, creep, and shrinkage considerations. Similarly, for the curved bridges, different types of bearing arrangements are possible based on the following criteria, (i) to minimize the internal forces in the bridge deck and the bearings, and (ii) to avoid the translation of the expansion joint across the traffic direction. The following are the bearing systems for the curved bridges, Radial bearing layout: The bearings are oriented such that the translation in the bearings is allowed radially with respect to the fixed bearing as shown in figure 4. This minimizes the internal forces in the bridge deck due to longitudinal actions (thermal, creep, and shrinkage effects) and reduces the bearing forces but the expansion joint at the abutment has translation along and across the traffic direction

Introduction

I. INTRODUCTION

A 3-span continuous curved steel composite bridge, with each span measuring 40 meters, is modeled in MIDAS Civil to analyze the effects of a temperature load of 40°C on the bridge's bearing systems. The temperature load is applied to evaluate how expansion and contraction influence the bearings. The bridge's superstructure is represented as a grillage model using frame elements. Longitudinal girders are used to simulate the composite stiffness of the deck, while transverse girders represent the transverse deck stiffness. Constraints are applied at the bearing locations as per the specified bearing system. Node-local axes are defined to align the support constraints in specific directions.

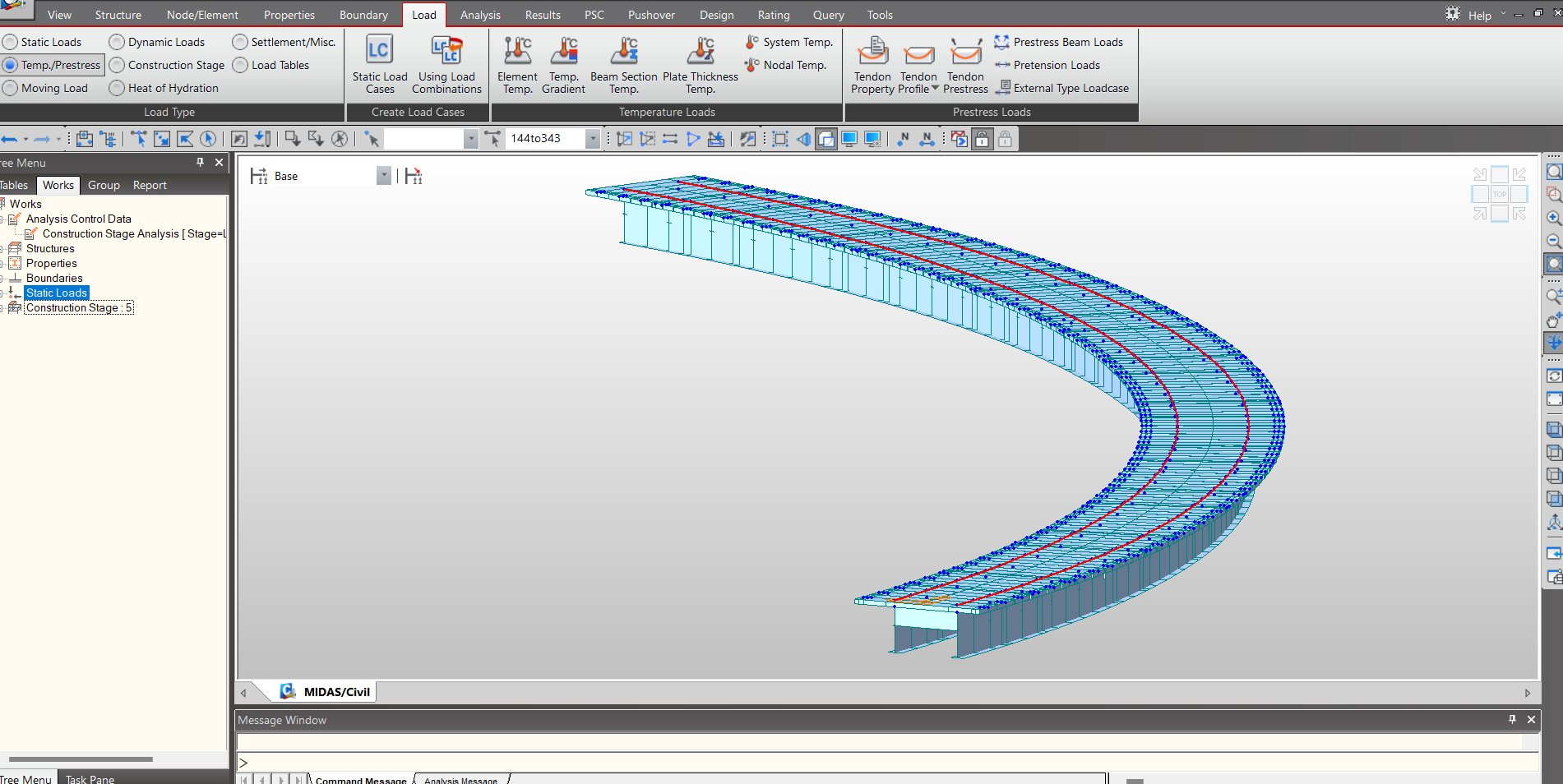
Figure 1 Midas Model

II. MODEL DETAILING’S

A. Model 01

Physical properties are same but the boundary condition changes and it is stated in two cases, as follows.

Table 1 Types of Cases

B. Codal Provision

For this thesis, ASC II code is considered for analysis, the bridge design adheres to the ASC II (American Steel Construction II) code, which provides detailed guidance on various aspects of structural design, including load types, boundary conditions, and bearing systems. The code addresses primary loading conditions such as dead loads, live loads, wind loads, thermal effects, and dynamic loads, ensuring the structure can withstand both static and transient forces.

Boundary conditions are carefully defined to represent realistic support constraints, including fixed, pinned, and sliding supports, allowing for accurate simulation of the bridge's behavior under operational and environmental conditions. The design also incorporates detailed specifications for bridge bearings, which accommodate movements due to thermal expansion, contraction, and structural deformation, while ensuring stability and load transfer between the superstructure and substructure. These considerations align with the ASC II code's requirements for safety, serviceability, and durability.

III. COMPARATIVE TABLES

A. Comparative Table for the Maximum Reaction and the Node Number

Table 2  Comparative Table for the Maximum Reaction and the node number.

• Key Observation: The maximum reaction force is slightly lower in the case with elastic links (221.63 kN) compared to the rigid link case (225.77 kN), with the node numbers being 682 and 625, respectively.

B. Comparative Table for the minimum Reaction

Table 3 Comparative Table for the minimum Reaction

• Key observation: The minimum reaction force in the local direction is more negative for the elastic links case (-13.25 kN) compared to the rigid link case (-2.18 kN), with the node numbers being 3 and 4, respectively.

C. Comparative Table for the Maximum Deformation (mm)

Table 4 Comparative Table for the Maximum Deformation (mm)

• Key Observation: The deformation in the elastic links case (49.45 mm) is slightly higher than in the rigid link case (49.43 mm), with the node numbers being 6 and 4, respectively.

D. Comparative Table for the Minimum Deformation (mm)

Table 5 Comparative Table for the Minimum Deformation

• Key Observation: n the elastic links case, the deformation at the traffic across direction is 0.504651 mm, while it is 0 mm in the rigid link case, with both occurring at node 5.

E. Comparative Table for the Maximum and Minimum Truss force (mm)

Table 6 Comparative Table for the Maximum and Minimum Truss force (mm)

• Key observation: In the comparison of maximum forces, the rigid link case shows a maximum force of -151.61848 kN at element 14, whereas the elastic links case shows a higher maximum force of -253.74411 kN at element 29. For minimum forces, the rigid link case shows -37.805567 kN at element 15, while the elastic links case shows -21.762756 kN at element 22. The elastic links case demonstrates both higher maximum and minimum forces compared to the rigid link case.

F. Maximum and Minimum Beam forces, moment and torsion in Rigid Link

Table 7 Maximum and Minimum Beam forces, moment and torsion in Rigid Link

G. Maximum and Minimum Beam forces, moment and torsion in Elastic Link

Table 8 Maximum and Minimum Beam forces, moment and torsion in Elastic Link

• Key Observation: The elastic link case has higher maximum axial force and torsion compared to the rigid link case, but the rigid link case exhibits much higher maximum moment-y and shear forces.

Conclusion

The results of this analysis indicate that rigid links provide higher resistance to thermal deformation, leading to greater reaction forces and lower displacement. These characteristics make rigid links more suitable for applications where stiffness and minimal deformation are critical. Conversely, elastic links offer increased flexibility, resulting in higher axial forces, moments, and torsion. This flexibility allows them to absorb and redistribute forces more effectively, which can be advantageous in dynamic conditions or structures where deformation is allowed or desired. Ultimately, the decision between using rigid or elastic links should be based on the specific needs of the structure. Rigid links are better suited for situations where minimal displacement and maximum stiffness are required, while elastic links may be preferable in conditions where flexibility and the ability to adapt to thermal expansion are more important. Further testing and optimization could refine the application of these findings to real-world structural designs.

References

[1] American Association of State Highway and Transportation Officials (AASHTO). (2014). “Standard Specifications for Highway Bridges”. Washington, DC: AASHTO. [2] Beardsmore, R., & Lambert, S. (2011). “Bridge Design and Assessment: A Guide to Load Rating and Evaluation”. London: Thomas Telford. [3] Boon, A. P., & De Jong, R. M. (2015). “Bridge Bearings and Their Applications”. Journal of Bridge Engineering, 20(7), 04014094. [4] Bournas, D. A., & Kourkoulis, R. A. (2013). “Performance of Bridge Bearings under Dynamic Loads”. International Journal of Bridge Engineering, 12(4), 273-282. [5] Cudny, W., & Kalinski, R. (2007). “Innovative Bridge Bearing Solutions”. Structural Engineering Review, 14(3), 98-106. [6] Dennis, J., & McManus, W. (2014). “Analysis of Elastomeric Bearings in Bridge Engineering”. Journal of Structural Engineering, 141(6), 04014122. [7] Dinesh, R., & Prakash, M. (2018). “Design and Performance of Bridge Bearings: A Comparative Study”. International Journal of Civil Engineering and Technology, 9(5), 303-313. [8] Fischer, G., & Harper, R. (2009). “Bridge Bearings: Types and Applications”. International Journal of Bridge Engineering, 8(2), 101-107. [9] Frey, M., & Singh, N. (2010). “The Role of Bearings in the Seismic Performance of Bridges”. Journal of Bridge Engineering, 15(2), 89-96. [10] Ghosh, S., & Bhaduri, S. (2017). “Numerical Modeling of Bearings in Bridges: A Review”. Journal of Civil Engineering, 45(3), 278-286. [11] Ibrahim, A., & Loo, W. (2012). “Recent Advances in Bridge Bearing Design and Materials”. Structural Concrete, 13(4), 345-355. [12] Jain, M., & Saini, R. (2019). “Bridge Bearings for Seismic Applications: A Review”. Journal of Earthquake Engineering, 23(4), 451-460. [13] Kumar, A., & Verma, R. (2018). “Performance of Composite Bearings in Bridge Structures”. Structural Engineering Journal, 12(2), 132-140. [14] Liu, Z., & Li, H. (2013). “The Impact of Temperature Changes on Bridge Bearings”. Journal of Bridge Engineering, 18(9), 04014109. [15] Mathur, A., & Sharma, S. (2011). “Dynamic Response of Bearings under Seismic Loading”. Structural Dynamics Journal, 15(6), 245-258. [16] Moser, R., & Richards, T. (2015). “Bridge Bearings and Their Role in Modern Bridge Design”. Bridge Design Journal, 7(2), 58-66. [17] National Cooperative Highway Research Program (NCHRP). (2016). “Guidelines for Seismic Design of Highway Bridges”. Washington, DC: Transportation Research Board [18] Ramachandran, R., & Yadav, S. (2016). “Performance of Bearings in Curved Bridges”. International Journal of Bridge Engineering, 18(4), 171-180. [19] Rao, S., & Pate, J. (2014). “Fatigue Resistance of Bearings under Repeated Loadings”. Journal of Structural Engineering, 14(3), 89-96. [20] Shehata, H., & Roberts, A. (2012). “Bridge Bearing Testing and Evaluation Techniques”. Journal of Testing and Evaluation, 40(4), 865-875. [21] Singh, S., & Sood, A. (2017). “Elastomeric Bearings in Bridges: State of the Art”. Journal of Bridge Engineering, 22(5), 04017008. [22] Smith, A., & Paton, B. (2010). “Innovative Bearing Solutions for Modern Bridges”. Engineering Structures, 32(11), 3351-3359. [23] Spence, S., & Foster, L. (2011). “Materials for Bridge Bearings: Trends and Developments”. Materials Science and Engineering, 30(6), 1013-1020. [24] Toh, R., & Chia, W. (2019). “Seismic Resilience of Bridge Bearings: A Case Study”. Earthquake Engineering Journal, 24(5), 812-820. [25] Yadav, N., & Bansal, P. (2017). “Experimental Study on the Performance of Bridge Bearings”. Journal of Materials in Civil Engineering, 29(4), 04017045. [26] Zhang, L., & Wang, Y. (2014). “Optimization of Bearing Systems for Seismic Bridge Design”. Engineering Structures, 75(1), 79-88. [27] Zhang, Z., & Zhou, X. (2013). “Bridge Bearings under Thermal Expansion and Contraction”. Journal of Structural and Civil Engineering, 14(2), 202-210. [28] Zhou, X., & Zhang, Y. (2016). “The Future of Bridge Bearing Technologies”. Modern Civil Engineering, 25(3), 124-133. [29] International Association for Bridge and Structural Engineering (IABSE). (2015). “Design of Bridge Bearings for Modern Infrastructure”. Zurich, Switzerland: IABSE Publications. [30] U.S. Federal Highway Administration (FHWA). (2017). “Bridge Bearings and Expansion Joints: Guidelines for Design and Maintenance”. Washington, DC: FHWA.

Copyright

Copyright © 2024 Shiril Mishra, Dr. Raghvendra Singh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.