Design and Implementation of Encryption/ Decryption Architectures for BFV Homomorphic Encryption Scheme

Abstract

Now a days security is the prime part for both, the satellites communication of the electronics data and the stored data, hence encryption is important for information processing system and communication network. The proposed approach is easy to learn due the use of speed efficient Vedic multiplier. Since it minimizes the execution time and area, so the delay and power consumption is further decrease by the compact and flexible approach in the Mix column transform which takes different approach rather than conventional multiplication previously. The structure style of modeling helps to easy understandable the proposed design of algorithm. BFV is the symmetrical has designed and verified in the Verilog HDL in Xilinx tool. In this project we present using kogge-stone adder and Vedic multiplier.

Introduction

I. INTRODUCTION

Since there is an evolution of wireless communication, the encrypting of data are major concern as shown in figure 1. Encryptions is the process of transfer of input text data (plain text) into the unintelligent data (cipher text) with the help of well algorithm are defined but U.S. government adopted that be used in the federal departments and agencies for protecting the important Information. According to the specifications of AES On October 2000, the NIST (national Institute of standard and technology) announced that AES encrypting algorithm as the best from other encrypting technique in the field of security, performance, efficiency, implementation capability and simplicity. Cryptography is the recognition and avoidance from the fraud and other illegal activity. The proposed AES design is the symmetric-key cryptography which involves the secret key that is only known by the user, which having the same number of bits as the Palin text i.e. 128 bits. It considered that the secret key for the encryption and decryption of block of data. As for the symmetry system the secret key must be shared between the sender and the receiver for the communications purpose decrypt data. The AES process is realizing in ATM, intelligence card and magnetism card.                                    

Cryptography enables you to store sensitive information or transmit it across insecure networks (like the Internet) so that it cannot be read by anyone except the intended recipient. While cryptography is the science of securing data, cryptanalysis is the science of analyzing and breaking secure communication. Classical cryptanalysis involves an interesting combination of analytical reasoning, application of mathematical tools, pattern finding, patience, determination, and luck. Cryptanalysts are also called attackers. Cryptology embraces both cryptography and cryptanalysis growth is a focal limit in math exercises subject to this assignment, for instance, Multiply and Accumulate (MAC) and inner thing are among a bit of the regularly used Computation Intensive Math Functions (CIAF)currently realized in various Digital Signal Processing (DSP)applications, for instance, convolution, Fast Fourier Transform (FFT), isolating and in chip in its math and justification unit. Since increase overpowers the execution time of most DSP estimations, so there is a need of quick multiplier. At this moment, increment time is so far the prevalent factor in choosing the direction procedure length of a DSP chip.

A. Problem Statement

In conventional IP forwarding, the router uses a longest-prefix match on the destination IP address to determine where to forward a packet. With MPLS, labels are attached to packets at the ingress point to an MPLS network. Within the network, the labels are used to route the packets, without regard to the original packet header information. These labels can be stacked as a last in first out (LIFO) label stack, enabling MPLS flows to be combined for transport and separated later for distribution. Current proposed protocols for MPLS security, Behringer [2] and Senevirathne et al. [3] discuss two approaches to securing MPLS. Behringer [2] makes the assumption that the core MPLS network is "trusted and provided in a secure manner." We make no such assumption in our work. We assume that only the MPLS nodes themselves are secure. The physical links connecting the nodes are assumed to not be secure – we protect them using our protocol. Senevirathne et al. [3] proposes an encryption approach using a modified version of IPsec. IPsec is defined by the IETF [4], and is an all-purpose encryption protocol that includes key distribution, authentication for the IP header, and authentication and encryption for the IP payload. Senevirathne et al.

II. EXISITING SYSTEM

Here, we first present our Montgomery modular multiplier hardware architecture and its implementation. We then explain two encryption/decryption hardware architectures implementing the iterative and the four-step Cooley-Tukey NTT algorithms for polynomial multiplication operation, respectively. Henceforth, they are shortly referred to as the iterative hardware and the four-step hardware, Here, we first present our Montgomery modular multiplier hardware architecture and its implementation. We then explain two encryption/decryption hardware architectures implementing the iterative and the four-step Cooley-Tukey NTT algorithms for polynomial multiplication operation, respectively. Henceforth, they are shortly referred to as the iterative hardware and the four-step hardware, respectively.

III. PROPOSED SYSTEM

In this proposed system we can work on internal blocks like adder and multiplier Extension: Vedic multiplier with koggestone adder which fast in process compare to other Architure will be same but this block is multiplier and adder block is replaced with extension work of adder and multiplier.

A. Kogge Stone Adder

Kogge stone adder is a parallel prefix type of carry look forward adders. It comprises of four vertical stages; every vertical phase of Kogge stone adder creates an engender and produce bit. It is considered as the quickest adder and it is broadly utilized in businesses for superior of arithmetic circuits. In Kogge stone adder carries are registered quick by processing them in parallel at the expense of expanded territory. Kogge stone adder is adder which is having low delay.

1. Multipliers

The most basic type of the increase comprises of joining two numbers, the multiplier and the multiplicand, to shape the last item. The essential augmentation can be accomplished through the conventional paper and pencil technique, disentangled to radix 2.'

2. Multiplication Algorithm

From the above dialog it very well may be reasoned that the augmentation of two paired numbers has now changed in to the expansion of two twofold numbers. Considering this the increase of two double numbers might be detailed as pursues, i) If the Least Significant Bit of the multiplier is '1', the aggregator (at first set as '0') is included with the multiplicand. ii) Shift the multiplier and aggregator one piece to one side. iii) If the Least Significant Bit of the multiplier is '0', at that point just move the multiplier and aggregator one piece to one side. iv) Repeat steps (i) to (iii) till every one of the bits in the multiplier are inspected.

3. Power Optimization in Multipliers

Power decrease in multipliers should be possible at all plan levels beginning from the innovation level to the framework level. In the multipliers, the incomplete item age, decrease and last stages are structured as a combinational plan.

They have a huge plan with high entryway thickness, in certainty high transistor thickness. Clearly this huge dynamic region gives space to have extensive power utilization. In the combinational structure, the exchanging movement chooses the power scattering. Consequently, the power scattering in the multipliers can be diminished by limiting the exchanging exercises. Another effective methodology is by decreasing the quantity of fractional items created in the multiplier structure and their wiring. Duplication is a fundamental necessity in the present high complex processors. Parallel increase is performed by a two-level activity, the age of the halfway items and their collection.

4. Proposed Hybrid Vedic Multiplier

The multipliers are the core of any fast-computational gadgets. In the multiplier circuits, the measure of the multiplier chooses the quantity of adders being utilized. Consequently, the power utilization relies upon the quantity of adder squares utilized and the methodology pursued to interface the adder squares to play out the increase activity. Since all the constant applications utilize the multipliers as their center component, the multipliers are the significant power devouring squares. Ordinarily bigger squares are constructed utilizing different littler squares and power streamlining is centered around these littler squares.

Conclusion

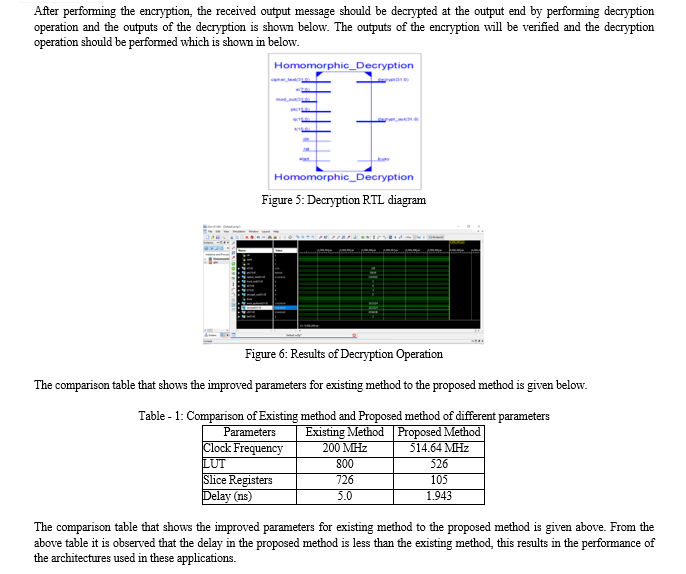
Here this Project We Can Reduce the Power Consumption and Delay by Using Vedic Multiplier and K koggestone Adder which is Fast in Performance. The greater values of frequency will result in the reduction in delay. So the performance of the system will be increased. And also, the number of LUT’s used in this project will also be reduced. This work can be used Furtherly for 128 bits, 256 bits, can be Implemented by Further Different Multipliers and Fastest Adder to Increase the Performance of the Circuit. Finally, with small modifications, the core arithmetic units in our accelerator can be used to implement ring arithmetic with larger ring degrees and modulus sizes. Currently, we are working on such new design based on our current architecture which reduce the power Consumption with Parallel prefix adder (like Kogge stone Adder), and the results will be presented in our future work.

References

[1] G. Oklobdzija, B. R. Zeydel, and H. Q. Dao, “Comparison ofhigh-performance VLSI adders in the energy-delay space,” in IEEETransactions on Very Large-Scale Integration (VLSI) Systems, vol. 13,no. 6, June 2005. [2] Jasbir Kaur and Lalit Sood, “Comparison between various types of addertopologies,” in IJCST, vol. 6, no. 1, Jan.–Mar. 2015. [3] Maroju SaiKumar and Dr. P. Samundiswary, “Design and performanceanalysis of various adders using verilog,” in International Journal ofComputer Science and Mobile Computing, IJCSMC, vol. 2, no. 9,pp. 128–138, Sep. 2013. [4] Nagendra, C.; Irwin, M.J.; Owens, R.M.,“Area-time-powertradeoffs in parallel adders”, Circuits and Systems II: Analog andDigital Signal Processing, IEEE Transactions on Volume 43, Issue10, Page(s): 689 – 702, 1996 [5] Min Cha and Earl E. Swartzlander, Jr, “Modified Carry SkipAdder for reducing first block delay”, Proc. 43rd IEEE MidwestSymp. on Circuits and Systems, Lansing MI, Page(s): 346-348,2000 [6] Pak K. Chan, et al, Delay Optimization of Carry-Skip Adders andBlock Carry-Lookahead Adders Using Multidimensional DynamicProgramming, IEEE Transactions on Computers, vol. 41, No. 8,pp. 920-93, 1992 [7] Wang, Y.; Pai, C.; Song, X., “The design of hybrid carrylookahead/carry-selectadders, Circuits and Systems II: Analog andDigital Signal Processing, IEEE Transactions on Volume 49, pp.16-24, 2002. [8] Jin-Fu Li, Jiunn-Der Yu, Yu-Jen Huang, “A Design Methodologyfor Hybrid Carry-Lookahead/Carry-Select Adders withReconfigurability”, IEEE, 2005 [9] Raminder Preet Pal Singh, Praveen Kumar, and BalwinderSingh,Performance Analysis of 32-Bit ArrayMultiplier with a Carry Save Adder and with a Carry Look Ahead Adder, Letters of International Journalof Recent Trends in Engineering, vol.2, no.6, pp. 83-89, Nov 2009. [10] P. M. Kogge and H. S. Stone,“A parallel algorithm for the efficientsolution of a general class of recurrence equations,”IEEETransactions on computers, vol. C-22, no. 8, pp. 786–793, Aug. 1973. [11] R Arun Sekar, Balaji G Naveen, A Gautami, B Sivasankari, “Highefficient carry skip adder in various multiplier structures”, Advances in Natural and Applied Sciences, Vol. 10, Issue 14, sep. 2016, pp. 193-198. [12] T.Prabakaran, R.ArunSekar,” High Performance Reversible Vedic Multiplier using Cadence 45nm Technology”, International Journal of Research and Advanced Development, Vol. 02, Issue 04, pp. 64-71, Oct. 2018. [13] B.RatnaRaju, D.V.Satish, “A High Speed 16*16 Multiplier Based On UrdhvaTiryakbhyam Sutra”, International Journal of ScienceEngineering and Advance Technology, IJSEAT, Vol 1, Issue 5, Oct. 2013. [14] KathiAnoosha, SasiKiran, “Design of High Speed Vedic Multiplier Using Carry Select Adder with Brent Kung Adder”,International Journal & Magazine of Engineering, Technology, Management and Research, Volume 3, Issue 10, October 2016. [15] M. Kathirvelu and Manigandan, “Design of Area Optimized, Low power, High Speed Multiplier using Optimized PDP full adder”, International Journal of Electrical Engg, ISSN 0974-2158, Volume 6, Number 2, pp. 173-185, June 2013.

Copyright

Copyright © 2024 Vaddi Hari Chandana, R.L.B. Prasad Reddy, Lakshmi Devi. Guduru. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.