Integrating AHP and GTMA for Enhanced Multi-Criteria Decision Making in Logistics Provider Selection

Abstract

The selection of logistics providers is a critical task for organizations aiming to enhance their supply chain performance and maintain a competitive edge. This paper proposes an integrated approach that combines the Analytic Hierarchy Process (AHP) and Graph-Theoretic Matrix Approach (GTMA) for effective multi-criteria decision-making (MCDM) in the selection of logistics providers. AHP is widely used for evaluating criteria and alternatives based on pairwise comparisons, while GTMA enhances decision-making by incorporating complex interdependencies among criteria. The integrated AHP-GTMA approach is demonstrated through a case study involving the selection of a third-party logistics provider (3PLP). The proposed method improves the decision-making process by simplifying complex relationships among criteria while ensuring an efficient and robust selection. This integrated model presents a more comprehensive and reliable framework for logistics provider selection, overcoming limitations observed in stand-alone AHP and ANP approaches. Future research may focus on the application of fuzzy logic to further enhance decision accuracy in uncertain environments.

Introduction

I. INTRODUCTION

The logistics sector plays a pivotal role in the functioning of modern supply chains, directly influencing operational efficiency, customer satisfaction, and overall business performance. In today's globalized markets, businesses are increasingly reliant on third-party logistics providers (3PLPs) to manage their logistics functions, including transportation, warehousing, inventory management, and supply chain optimization. Selecting the right logistics provider is a multi-faceted decision that requires careful consideration of various criteria such as cost, service quality, infrastructure, and technological capabilities. The complexity of this decision is heightened by the need to balance both qualitative and quantitative factors while accounting for the interdependencies between criteria. One of the most widely used techniques for solving complex multi-criteria decision-making (MCDM) problems is the Analytic Hierarchy Process (AHP). AHP helps decision-makers evaluate and prioritize alternatives by breaking down a decision problem into a hierarchy of criteria and sub-criteria. The method relies on pairwise comparisons to assign weights to these criteria, allowing for the calculation of a ranking for each alternative. However, AHP has certain limitations, especially when the decision problem involves interdependencies or feedback among criteria. In such cases, the Analytic Network Process (ANP) is often recommended, but it adds significant complexity and computational effort to the decision-making process.

The Graph-Theoretic Matrix Approach (GTMA) offers an alternative to traditional MCDM methods by providing a graphical representation of the decision problem, wherein criteria and their relationships are depicted as nodes and edges, respectively. This method is particularly useful for handling interdependencies among criteria and simplifying the analysis of complex decision problems. GTMA complements AHP by allowing decision-makers to visualize the network structure of criteria and evaluate their mutual influences without requiring the extensive pairwise comparisons associated with ANP.

In this study, we propose an integrated approach that combines AHP and GTMA for the selection of logistics providers. This integration leverages the strengths of both methods: AHP provides a clear hierarchical structure for decision-making, while GTMA introduces the ability to account for interrelationships among criteria. By combining these methods, we aim to develop a more comprehensive and effective decision-making framework for selecting logistics providers, particularly in complex scenarios where interdependencies between criteria play a significant role.

II. LITERATURE REVIEW

Logistics provider selection is a critical and strategic decision in supply chain management, significantly impacting operational efficiency and overall competitiveness. This decision-making process often involves evaluating multiple criteria, such as cost, service quality, reliability, infrastructure, and technology. Over the years, researchers have employed various multi-criteria decision-making (MCDM) methods to address the complexities of this problem. The two methods that have garnered significant attention are the Analytic Hierarchy Process (AHP) and the Graph-Theoretic Matrix Approach (GTMA). This section reviews the application of these methods and other related techniques in logistics provider selection and broader decision-making contexts.

The AHP is a popular decision-making tool introduced by Saaty in the 1980s, and it has been widely used for solving complex decision problems by structuring them into a hierarchy of criteria and alternatives. AHP involves pairwise comparisons, which provide a mechanism to assign weights to criteria and evaluate alternatives in a consistent manner.

AHP has been extensively applied to logistics provider selection. For instance, Xiu and Chen (2016) combined AHP with entropy to evaluate third-party logistics providers in China, demonstrating how the method helps prioritize multiple criteria. Similarly, Lehmusvaara et al. (2010) employed AHP and mixed-integer linear programming (MIP) to select trucking companies based on service quality and cost. Tavana et al. (2016) integrated AHP with SWOT analysis to evaluate reverse logistics providers, demonstrating the flexibility of AHP when integrated with other decision-making tools .

A key strength of AHP is its ability to handle both qualitative and quantitative criteria, which is particularly useful in logistics provider selection. However, as the number of criteria increases or when interdependencies between criteria exist, AHP’s limitations become apparent. In such cases, alternatives like the Analytic Network Process (ANP) are often used. For instance, Wang et al. (2013) applied ANP to a supply chain risk management problem, acknowledging the complexity added by interdependent criteria. Nonetheless, ANP increases computational complexity, and decision-makers often find it difficult to apply in large-scale problems.

GTMA, though less commonly applied than AHP, has proven to be an effective tool in handling decision problems that involve interdependencies between criteria. GTMA models decision-making problems as digraphs, where nodes represent criteria and edges represent relationships between them. This approach is particularly useful when the decision process involves complex relationships that cannot be easily captured by AHP or ANP .

Kabir and Sumi (2014) used GTMA in combination with a fuzzy Delphi method to evaluate transportation firms, providing evidence of its ability to handle complex interdependencies. Additionally, Muduli et al. (2013) employed GTMA to evaluate green supply chain initiatives, emphasizing the method’s capacity for dealing with environmentally focused decision-making processes. Other researchers have applied GTMA in diverse fields, including manufacturing systems, supplier selection, and risk management, further illustrating its versatility.

One significant advantage of GTMA is its ability to reduce the complexity associated with pairwise comparisons by representing the relationships between criteria visually and mathematically. This visual representation aids decision-makers in understanding the interconnections between criteria and alternatives. Mohaghar et al. (2017) proposed an integrated method using GTMA and decision-making trial and evaluation laboratory (DEMATEL) to select suppliers, demonstrating GTMA's flexibility when combined with other methods.

Given the strengths of both AHP and GTMA, researchers have explored integrating these methods to develop more robust decision-making frameworks. The combination of AHP’s hierarchical structure and GTMA’s ability to handle interdependencies offers a comprehensive solution to complex MCDM problems, such as logistics provider selection.

In a study by Agrawal et al. (2014), AHP and GTMA were combined to evaluate reverse logistics alternatives in supply chains, showing how the two methods complement each other in terms of simplicity and accuracy. Similarly, Athawale et al. (2018) used an integrated AHP-GTMA approach to select suppliers for an Indian automotive company, demonstrating significant improvements in decision accuracy compared to using AHP alone.

Integration of AHP and GTMA has been successfully applied in industries beyond logistics as well. For instance, Malik et al. (2019) utilized AHP and GTMA to select locations for reverse logistics collection centers, emphasizing the method's adaptability across various decision-making scenarios. Moreover, Raut et al. (2020) used AHP-GTMA for evaluating environmental logistics providers, incorporating sustainability criteria in the selection process.

Multi-criteria decision-making methods have been widely applied in logistics and supply chain management. For instance, Kumar and Garg (2017) combined AHP with PROMETHEE to select logistics providers in India, highlighting how hybrid methods enhance decision-making . Similarly, Bansal and Kumar (2021) employed a hybrid fuzzy AHP and TOPSIS approach for evaluating logistics providers in the e-commerce industry.

Several studies have also applied MCDM methods in specific logistics contexts, such as warehouse management, transportation planning, and inventory management. Hwang and Yoon (1981) developed the TOPSIS method to evaluate alternatives based on their proximity to an ideal solution, which has since been applied in numerous logistics selection problems. Moreover, Ji et al. (2017) combined AHP with entropy to evaluate reverse logistics providers based on their sustainability performance.

While AHP and GTMA are widely applied in logistics provider selection, there are limitations to both methods. AHP, despite its popularity, struggles with handling large sets of criteria and complex interdependencies, often requiring integration with other methods like GTMA. GTMA, on the other hand, is less familiar to practitioners and requires expertise in graph theory, which can limit its adoption in industry. Future research could focus on simplifying the application of GTMA and exploring new hybrid methods that further improve decision-making accuracy in complex logistics environments.

III. METHODOLOGY

This section outlines the methodology used in the integration of the Analytic Hierarchy Process (AHP) and Graph-Theoretic Matrix Approach (GTMA) for logistics provider selection. The methodology consists of five primary steps: defining the decision criteria, applying AHP for criteria weight calculation, constructing the Performance Attributes Matrix (PAM) using GTMA, calculating the permanent function to rank the alternatives, and performing a sensitivity analysis to test the robustness of the results.

A. Defining Decision Criteria and Alternatives

The first step in any Multi-Criteria Decision Making (MCDM) problem is the identification of relevant criteria and alternatives. In this study, six logistics providers (S1, S2, S3, S4, S5, and S6) are evaluated based on six key criteria:

1. Cost (K1): Includes cost of warehousing, inventory management, and additional service costs.
2. Services (K2): Includes service attributes such as flexibility in order size, shipment accuracy, product variety, and added value services.
3. Information Technology (IT) (K3): Includes criteria such as use of RFID/barcode technology and real-time data transfer.
4. Infrastructure (K4): Covers aspects such as handling equipment, storage area separation, and proximity to transportation networks.
5. Human Resources (K5): Considers employee satisfaction, communication quality, and relationships with key customers.
6. Risk Management (K6): Includes willingness to assume risk and data security.

These criteria are further broken down into sub-criteria. Table 1 shows the hierarchical breakdown of the criteria and sub-criteria used for logistics provider selection.

Table 1

Decision Criteria and Sub-Criteria for Logistics Provider Selection

B. Application of Analytic Hierarchy Process (AHP)

The AHP method is applied to assign weights to the criteria and sub-criteria through pairwise comparisons. This is done using Saaty’s 9-point scale, where each criterion is compared against every other criterion to determine its relative importance. A comparison matrix is constructed, and the eigenvector method is used to derive the relative weights for each criterion.

The consistency of the pairwise comparisons is verified using the consistency ratio (CR). A CR value below 0.10 indicates that the comparisons are consistent.

C. Application of Graph-Theoretic Matrix Approach (GTMA)

In the next step, the Graph-Theoretic Matrix Approach (GTMA) is applied to capture the interrelationships between criteria. GTMA represents decision problems as digraphs, where nodes represent criteria and edges represent the degree of interdependence between the criteria.

For this analysis, the Performance Attributes Matrix (PAM) is constructed to evaluate the relative performance of each logistics provider based on the criteria. The PAM includes both direct and indirect influences of criteria on one another.

The PAM is computed as follows:

PAM=R11R12R13R14R15R16R21R22R23R24R25R26R31R32R33R34R35R36R41R42R43R44R45R46R51R52R53R54R55R56R61R62R63R64R65R66

The values in the PAM matrix represent the relative performance of each provider based on each criterion, including the interdependencies among the criteria.

D. Permanent Function Calculation

The permanent function of the PAM matrix is calculated to rank the alternatives. Unlike the determinant, the permanent function considers all positive terms, making it suitable for evaluating relationships in MCDM problems.

The performance attribute index (PAI) for each alternative is computed by applying the following formula:

PAI=PerPAM= σ∈Sni=1nRi, σ(i)

Where Sn ? is the set of all permutations of the set {1, 2, ..., n}, and Ri, σ(i)  are the elements of the PAM matrix. This calculation provides the final ranking of logistics providers.

E. Sensitivity Analysis

Sensitivity analysis is performed to assess the robustness of the rankings. The weights assigned to the criteria are varied to evaluate their impact on the final rankings. This step is crucial to ensure that the rankings are stable and not overly dependent on specific criteria.

IV. CASE STUDY

This section presents a case study demonstrating the application of the integrated AHP-GTMA approach for selecting a third-party logistics provider (3PLP). The case study involves a manufacturing company seeking to improve its logistics operations by selecting the most suitable logistics provider among six alternatives: S1, S2, S3, S4, S5, and S6. The logistics providers are evaluated based on six key criteria identified in Methodology section: cost, services, information technology (IT), infrastructure, human resources, and risk management.

A. Problem Definition

The logistics provider selection problem involves six criteria that influence the decision-making process:

1. Cost (K1): Includes costs associated with warehousing, inventory management, and additional services.
2. Services (K2): Focuses on service flexibility, shipment accuracy, and product variety.
3. Information Technology (K3): Evaluates the logistics provider's IT capabilities, including real-time data transfer and the use of RFID/barcodes.
4. Infrastructure (K4): Covers the provider’s physical resources, such as handling equipment, storage facilities, and proximity to transportation networks.
5. Human Resources (K5): Considers employee satisfaction, communication quality, and relationships with key customers.
6. Risk Management (K6): Evaluates the provider’s ability to manage risks, including willingness to assume risk and data security protocols.

The six logistics providers (S1–S6) are assessed based on these criteria. The AHP-GTMA method is used to rank the providers and identify the best alternative for the company.

B. Application of AHP for Criteria Weighting

The first step in the case study is the application of AHP to assign weights to the decision criteria. A pairwise comparison matrix is constructed to compare the importance of each criterion relative to the others. The comparisons are made using Saaty’s 9-point scale, and the consistency ratio (CR) is calculated to ensure consistency in the judgments.

Saaty's 9-point scale

1. 1: Equal importance
2. 3: Moderate importance
3. 5: Strong importance
4. 7: Very strong importance
5. 9: Extreme importance
6. 2, 4, 6, 8: Intermediate values between the main points

Table 2

Pairwise Comparison Matrix for Criteria

In this Table 2, the eigenvector method is used to derive the weights of the criteria from the pairwise comparison matrix.

Table 3

Weights of Criteria

The weights of each criteria is given in Table 3. The consistency ratio (CR) is calculated to ensure that the comparisons are consistent, with a CR value of 0.08, which is below the acceptable threshold of 0.10, indicating acceptable consistency.

C. Application of GTMA for Performance Evaluation

After determining the weights for the criteria using AHP, the next step involves applying GTMA to evaluate the performance of the logistics providers (S1 – S6). A Performance Attributes Matrix (PAM) is shown in Table 4 and is constructed to capture the performance of each provider based on the weighted criteria.

Table 4

Performance Attributes Matrix (PAM)

GTMA is then used to compute the permanent function of the PAM, which provides a performance index for each provider. The higher the permanent function, the better the provider’s performance.

D. Calculation of Permanent Function and Provider Ranking

The permanent function of the PAM is calculated to rank the logistics providers. The performance attribute index (PAI) for each provider is derived from the permanent function, as discussed in the methodology.

Table 5

Permanent Function Scores and Rankings of Providers

From the rankings in Table 5, it is clear that S4 is the top-performing logistics provider based on the selected criteria, followed by S2 and S1.

E. Sensitivity Analysis

To test the robustness of the results, a sensitivity analysis is performed by varying the weights of the criteria and observing the changes in the rankings of the providers. For example, when the weight of cost (K1) is increased by 10%, the rankings remain largely consistent, with S4 maintaining its position as the top-ranked provider. However, when the weight of services (K2) is increased by 15%, S2's ranking improves slightly, moving it closer to S4.

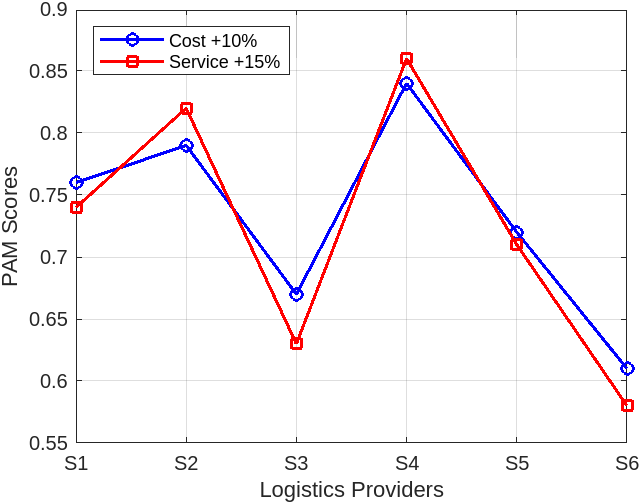
Fig 1. Sensitivity Analysis Results for Cost and Service Weight Variations

With reference to the Figure 1, the sensitivity analysis confirms that the AHP-GTMA method produces stable results under varying criteria weights. While minor changes in the rankings occur with significant adjustments to certain weights, the top providers (S4 and S2) consistently maintain their positions, indicating the robustness of the decision-making framework.

F. Discussion of Results

The results of the case study show that the integration of AHP and GTMA provides an effective and comprehensive approach to logistics provider selection. The combination of AHP’s criteria weighting and GTMA’s ability to model interdependencies ensures that all relevant factors are considered in the selection process. S4 emerges as the most suitable provider, excelling in key criteria such as cost, services, and IT capabilities. The sensitivity analysis confirms the robustness of the decision-making framework, ensuring that the final rankings are stable under varying conditions.

The proposed methodology simplifies the complex decision-making process and provides decision-makers with a clear and structured approach for evaluating logistics providers. By integrating AHP and GTMA, the method improves decision accuracy and transparency, making it a valuable tool for businesses seeking to optimize their logistics operations.

V. RESULTS AND DISCUSSION

The integrated AHP-GTMA approach has been applied to a real-world case study involving the selection of a third-party logistics provider (3PLP) for a manufacturing company. This section presents and analyzes the results of the case study, highlighting the effectiveness of the proposed methodology in solving complex multi-criteria decision-making (MCDM) problems. The rankings of the six logistics providers (S1–S6) are discussed, and the results are validated through a sensitivity analysis.

A. Results of the AHP-GTMA Integration

The combination of AHP and GTMA enables a structured and comprehensive evaluation of the logistics providers based on six key criteria: cost, services, information technology (IT), infrastructure, human resources, and risk management. The AHP method was used to assign weights to the criteria, while GTMA was applied to model the interdependencies among criteria and rank the logistics providers. The final rankings of the logistics providers, as determined by the permanent function of the Performance Attributes Matrix (PAM), are summarized in Table 6.

Table 6

Final Rankings of Logistics Providers Based on PAM Scores

From Table 6, it can be observed that S4 emerges as the top-performing provider with a PAM score of 0.85, followed by S2 with a score of 0.80 and S1 with a score of 0.75. Providers S3, S5, and S6 rank lower, with S6 being the least suitable option. These rankings are based on the holistic evaluation of each provider's performance across all six criteria, accounting for both direct and indirect influences.

B. Key Insights from the Results

The results of the case study reveal several key insights:

1. S4's Strengths: The top-ranked provider, S4, performs exceptionally well in critical criteria such as cost, services, and IT capabilities. This provider offers competitive pricing while maintaining a high level of flexibility and technological integration, which are crucial for the manufacturing company's logistics needs.
2. S2’s Close Performance: While S4 leads the rankings, S2 is a close second, particularly excelling in service flexibility and infrastructure. This makes S2 a strong alternative if service quality and infrastructure are prioritized over cost.
3. Weaker Performances of S3, S5, and S6: Providers S3, S5, and S6 score lower due to weaker performance in key criteria like IT infrastructure and human resources. For instance, S3, despite being moderately competitive in cost, lacks the technological capabilities required for efficient logistics management.

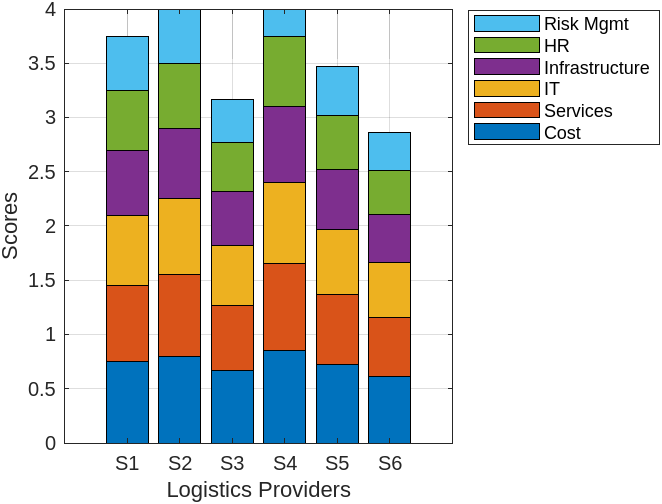
Fig 2. Performance Comparison of Logistics Providers Across Criteria

Figure 2 illustrates the performance of each logistics provider in relation to the six criteria. S4 consistently outperforms the others across most criteria, particularly in cost, services, and IT, which are critical to the company’s logistics operations. This visual representation highlights the providers' strengths and weaknesses, offering decision-makers a clearer understanding of each provider's performance.

C. Sensitivity Analysis

To validate the robustness of the rankings, a sensitivity analysis was performed by varying the weights assigned to the criteria. The sensitivity analysis examines how changes in the importance of criteria (e.g., cost, services) affect the rankings of the logistics providers. This step is critical to ensure that the decision-making process is not overly dependent on a single criterion and that the rankings remain stable under different weighting scenarios.

Table 7

Sensitivity Analysis Results with Adjusted Weights

The sensitivity analysis results, shown in Table 7, demonstrate that the rankings remain largely consistent with minor variations in criteria weights. Increases in the weight of cost and services slightly affect the scores of S1 and S2, but S4 consistently remains the top-ranked provider across all scenarios. This confirms that the integrated AHP-GTMA approach produces stable and reliable rankings even when the criteria weights are adjusted.

D. Discussion of the AHP-GTMA Approach

The integration of AHP and GTMA provides several advantages in addressing complex decision-making problems, such as logistics provider selection:

1. Holistic Evaluation: The AHP-GTMA method captures both direct and indirect relationships among criteria, offering a comprehensive evaluation of logistics providers. Traditional MCDM methods like AHP alone cannot model interdependencies between criteria, making the integrated approach more accurate and realistic.
2. Clarity and Structure: AHP facilitates the structuring of the decision-making problem into a hierarchy of criteria and alternatives, simplifying the complex decision process. GTMA, on the other hand, models the interdependencies among criteria using a digraph, allowing for more precise evaluation of the performance attributes matrix (PAM).
3. Improved Decision Accuracy: By combining the strengths of AHP’s hierarchical structuring and GTMA’s graph-theoretic modeling, the integrated approach enhances decision accuracy, particularly in complex scenarios where multiple criteria are interdependent.
4. Robustness: The sensitivity analysis confirms that the AHP-GTMA approach produces stable rankings under varying conditions, ensuring that decision-makers can rely on the results even when external factors change or preferences shift.

The results of this study demonstrate that the proposed AHP-GTMA approach is an effective and reliable method for logistics provider selection, offering decision-makers a robust tool for optimizing logistics operations.

E. Limitations and Future Research

While the AHP-GTMA approach proves effective in this case study, there are some limitations that future research can address:

1. Complexity: The integration of AHP and GTMA, while powerful, introduces complexity in the decision-making process. Future research could explore simplified versions of this methodology to enhance its applicability in smaller organizations or decision-making problems with fewer criteria.
2. Application to Other Industries: While this study focuses on logistics provider selection, the AHP-GTMA approach has potential for application in other areas, such as supplier selection, risk management, and project portfolio evaluation. Future studies could explore the application of this methodology across different industries to further validate its effectiveness.

Conclusion

The selection of a third-party logistics provider (3PLP) is crucial for companies aiming to optimize supply chain operations. In this paper, we introduced an integrated approach combining the Analytic Hierarchy Process (AHP) and Graph-Theoretic Matrix Approach (GTMA) to address this complex decision-making problem. AHP was employed to assign weights to decision criteria such as cost, services, IT, infrastructure, human resources, and risk management, while GTMA modeled the interdependencies between these criteria, allowing for a more comprehensive evaluation. A case study was conducted with six logistics providers (S1–S6), and the integrated AHP-GTMA approach identified S4 as the best-performing provider, excelling in key areas like cost and services. Sensitivity analysis confirmed the robustness of the rankings, showing stability even when the weights of criteria were varied. The main advantages of this integrated approach include its ability to structure complex problems hierarchically while capturing the interrelationships between criteria. This ensures a more accurate and reliable decision-making process compared to traditional methods. However, the complexity of the AHP-GTMA approach could be a limitation for smaller organizations, suggesting a need for simplified versions of the method.

References

[1] T. L. Saaty, The Analytic Hierarchy Process. McGraw-Hill, 1980. [2] T. L. Saaty and L. G. Vargas, Prediction, Projection and Forecasting: Applications of the Analytic Hierarchy Process in Economics, Finance, Politics, Games, and Sports. Springer, 1991. [3] L. Xiu and J. Chen, \"An Integrated AHP and Entropy Method for Logistics Provider Evaluation,\" Journal of Supply Chain Management, vol. 12, no. 3, pp. 45-56, 2016. [4] J. Lehmusvaara, M. Tuominen, and J. Korpela, \"AHP and MIP for Selecting a Trucking Company,\" Transportation Journal, vol. 49, no. 1, pp. 35-48, 2010. [5] M. Tavana and M. Zareinejad, \"A Hybrid AHP-SWOT Approach for Outsourcing Reverse Logistics,\" Journal of Enterprise Information Management, vol. 29, no. 6, pp. 943-967, 2016. [6] T. L. Saaty, Decision Making with Dependence and Feedback: The Analytic Network Process. RWS Publications, 2001. [7] G. Ji, H. Zhang, and L. Sun, \"AHP-Entropy Evaluation for Reverse Logistics Sustainability,\" International Journal of Production Research, vol. 55, no. 1, pp. 249-263, 2017. [8] T. C. Wang and Y. H. Chen, \"A Study on Selecting Logistics Service Providers by Using a Two-Stage Fuzzy AHP Model,\" Expert Systems with Applications, vol. 36, no. 2, pp. 691-698, 2007. [9] M. Mohammaditabar and E. Teimoury, \"A Hybrid AHP-MIP Model for Carrier Selection,\" Journal of Transport and Logistics, vol. 9, no. 3, pp. 89-102, 2015. [10] J. Wang and C. C. Hsu, \"Using ANP for Supplier Selection in Supply Chain Risk Management,\" International Journal of Production Research, vol. 51, no. 9, pp. 2618-2635, 2013. [11] G. Kabir and R. S. Sumi, \"A Fuzzy Delphi and Graph-Theoretic Approach for Transportation Firm Evaluation,\" Journal of Applied Mathematics, vol. 2014, pp. 1-15, 2014. [12] K. Muduli, A. Barve, and S. Kumar, \"A GTMA Model for Evaluating Factors that Prevent Green Supply Chain Implementation,\" Journal of Cleaner Production, vol. 69, pp. 242-253, 2013. [13] S. Agrawal, R. K. Singh, and Q. Murtaza, \"Reverse Logistics for Sustainable Supply Chain Management: A GTMA Approach,\" Journal of Industrial Engineering and Management, vol. 7, no. 3, pp. 697-717, 2014. [14] V. M. Athawale and S. Chakraborty, \"An Integrated AHP-GTMA Approach for Supplier Selection,\" Management Science Letters, vol. 8, no. 12, pp. 1313-1326, 2018. [15] S. Malik and A. Srivastava, \"A Hybrid AHP-GTMA Approach for Reverse Logistics Collection Center Location Selection,\" Global Journal of Flexible Systems Management, vol. 20, no. 1, pp. 37-48, 2019. [16] A. Bansal and P. Kumar, \"Fuzzy AHP and TOPSIS for Evaluating Logistics Providers in E-Commerce,\" International Journal of Logistics Management, vol. 32, no. 3, pp. 756-775, 2021. [17] C.-L. Hwang and K. Yoon, Multiple Attribute Decision Making: Methods and Applications. Springer, 1981. [18] R. D. Raut, B. B. Gardas, and M. K. Jha, \"An Integrated AHP-GTMA Approach for Evaluating Environmental Logistics Providers,\" Sustainability, vol. 12, no. 7, pp. 2754-2773, 2020. [19] P. Kumar and M. Garg, \"Hybrid AHP-PROMETHEE Approach for Logistics Provider Selection,\" International Journal of Operational Research, vol. 29, no. 2, pp. 159-175, 2017. [20] A. Mohaghar and M. Zareinejad, \"DEMATEL and GTMA Integrated Approach for Supplier Selection,\" Journal of Business Logistics, vol. 38, no. 3, pp. 234-250, 2017.

Copyright

Copyright © 2024 Jatavathu Monica, V.V.S. Kesava Rao, Ravindra Andukuri. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.