Interferometers and Its Applications in Physics

Abstract

The interference phenomenon, which is usually brought about by the superimposition of electromagnetic waves, is employed by a collection of techniques collectively referred to as interferometry to gather data.[1] Interferometry is a helpful investigative tool in a number of fields, including astronomy, fibre optics, engineering metrology, optical metrology, oceanography, seismology, quantum mechanics, nuclear and particle physics, plasma physics, remote sensing, biomolecular interactions, surface profiling, microfluidics, mechanical stress/strain measurement, velocimetry, and optometry.[18]. Recently, they have even been able to identify almost undetectable gravitational wave motions [20]. Light interference has many real-world applications, particularly in the photonics and optics domains. Examples include holography, spectroscopy, laser interferometry, and optical coatings. It is also utilised in the areas of metrology, telecommunications, and microscopy [21].

Introduction

I. INTRODUCTION

Interferometry is a measurement technique that uses the phenomenon of wave interference (of radio, light, or sound waves). Certain properties of the waves themselves and the materials they interact with can be measured. Furthermore, methods for using light waves to investigate displacement changes are referred to as interferometry. In precision machining, displacement measurement interferometry is a widely used technique for mechanical stage motion control and calibration. [1]An interference pattern can be created when two light beams are used, usually by splitting one beam into two. These two beams can then overlap one another at that point. Due to the extremely small wavelength of visible light, even minute variations in the optical paths—that is, the distances between the two beams which can be identified since they will result in discernible shifts in the interference pattern. As a result, optical interferometry has been used for measurement purposes for more than a century. Later on, after lasers were invented, its accuracy was increased.[1]Albert A. Michelson created the first interferometer in the 1880s, which popularised the idea of light interference as a practical measuring tool. Interferometry still relies heavily on the fundamental ideas of the Michelson interferometer, despite advancements in technology and measurement precision over time.[1 ]A beamsplitter, also referred to as a half-silvered mirror, is added to two mirrors to create a Michelson interferometer. The partially reflecting half-silvered mirror/beam splitter divides light into two beams with distinct optical pathways; one beam is directed towards mirror 1 and the other towards mirror 2. These beams are reflected back at the mirrors before they reach the detector, where they recombine at the beam splitter. The interference fringe pattern is caused by the phase mismatch between the two trajectories that these two beams travel. Depending on which measurement the interferometer was being used for, the detector then assesses this pattern to ascertain the wave characteristics, material properties, or displacement of one of the mirrors.[1]

The XL-80 laser helps create a single, very stable wavelength source, which is necessary to produce an interference pattern with great precision (distinct fringes).There are several possible arrangements for the interferometer based on Michelson's theory, but the linear form is the most straightforward. The retro reflectors, which are two mirrors in the Michelson interferometer of the XL-80 laser system, are a kind of prism that returns incoming light to its original path perpendicularly. One of them is fastened to the reference arm's beam splitter. When its distance from the beam splitter changes, the other retroreflector produces the variable length measurement arm. [1]The laser beam (1) leaves the XL-80 laser head and splits into a transmitted beam and a reflected beam at the polarising beam splitter. Before they reach the detector, these beams are recombined at the beam splitter after being reflected back from the two retroreflectors. When the beams from the reference and measurement arms recombine at the beam splitter, the employment of retroreflectors guarantees that the beams are parallel. The recombined beam exhibits constructive or destructive interference upon reaching the detector. The two beams are in phase during constructive interference, and their peaks reinforce one another to produce a brilliant fringe. Contrarily, destructive interference happens when the beams are out of phase, cancelling out each other troughs and producing a dark fringe.[1]

It is possible to observe the interference between these two beams thanks to the detector's optical signal processing. The relative phases of the two beams are altered by the measurement arm shift. The intensity of the recombined light varies periodically as a result of this constructive and destructive interference cycle.

Every time the measurement arm/retroreflector is moved by 316.5 nm, or half the laser wavelength, there is a single cycle of intensity variation from light to dark to light. This results in a 633 nm optical path change, which is the wavelength of the laser. As such, the movement is quantified by using the following formula to ascertain the number of cycles [1]:

d = Nλ/2

where N is the number of crossing fringes, λ is the laser's wavelength (0.633 microns), and d is the displacement (measured in microns). Phase interpolation is used during these cycles to attain the enhanced resolution of 1 nm.

The stability and precision of the laser unit depend on how well the wavelength of the laser beam is understood; this has no bearing on the accuracy of the linear positional measurements. The refractive index of the air the laser beam travels through, which is influenced by the air's temperature, pressure, and relative humidity, determines the operating wavelength of the beam. For this reason, any changes in these parameters require the beam's wavelength to be modified, or corrected for.[1]

II. THEORY OF INTERFEROMETERS

A system of optical systems called interferometers can be configured for a wide range of uses,  including the identification of viruses, the detection of liquid changes brought on by contaminants or oxygen depletion, and the correction of atmospheric aberrations. Superposition is a fundamental characteristic of waves, including light, that allows two or more waves to occupy the same space at the same time. Unlike particles that collide when they attempt to occupy the same space at the same time, this is a fundamental property of all waves. When two waves overlap, they are joined together as a single unit. The general term for the superposition of two or more waves is interference. Three different outcomes can occur from two waves travelling in the same direction and having identical amplitude and frequency. In the absence of a phase delay, there is neither constructive or destructive interference between the waves. When the crests and valleys of both waves coincide, or are in phase, constructive interference occurs. When two waves are out of phase, destructive interference occurs, causing the crest of one wave to overlap with the trough of the other. It turns out that interference is a useful tool for explaining a broad variety of physical phenomena, such as standing waves, resonance, harmonics, diffraction gratings, hearing, and speech. An optical device that is frequently used and is easy to make precisely is the interferer. A light beam, typically a laser beam, is essentially divided into two parts by an interferometer: a reference beam and a sensor beam. The reference beam will follow an optical path that remains constant. If the optical pathway shifts, it will affect and modify the direction of the sensor beam. We want to keep an eye on the reason of that shift, whether it be gases, pressure, or temperature. When the two beams are recombined on a screen, the interference between them will produce an interference pattern [2]. Envision a scenario where you wish to determine the amount of a gas that is there. The sensor beam on your interferometer is designed to pass through a small, possibly vented petrol can that you may have. An empty container and a reference beam are used to calibrate the interferometer. The results can be evaluated by contrasting them with the interference pattern. For instance, we add a gas to the container whether nitrogen, contaminated air, or even a liquid that changes its refractive index. The optical route and interference pattern of the sensor beam will vary depending on the optical characteristics of the element under investigation.

III. TYPES OF INTERFEROMETERS

Interferometers come in various varieties. The most popular ones are Fabry-Perot, Michelson, and Mach-Zehnder. More configuration choices are available, though, and specialised performance can be achieved with a custom interferometer design. The most popular kinds of interferometers are described below, along with some information on their capabilities. [2] In Figure 1, a MZI is displayed. Two beams are produced from the collimated beam: a reference beam (RB) and a sensor beam (SB).  A beam splitter is used to recombine the two beams after they have travelled equal length optical pathways and reflected off a mirror.  Then, a single detector which is typically a CMOS camera that can be used to identify the interference pattern [2].

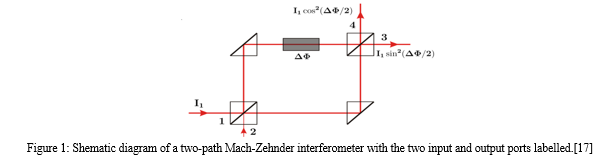
One form of interferometer used to measure the relative phase shift between two collimated light beams is the Mach-Zehnder interferometer. With two beam splitters and two mirrors, it is also an amplitude-based beam division interferometer. Unlike the Michelson-Morley interferometer, the Mach-Zehnder interferometer recombines beams downstream of the second beam splitter, with each beam taking a distinct path. However, the coherent superposition of the two waves is what causes the interference.[3] The first beam splitter divides the incoming light into two directions. Depending on the phase difference between the two waves, each beam reflects off a mirror before recombining at the end of the second beam splitter to generate an interference pattern. The phase difference, or equivalent optical path, can be purposefully produced by purposely creating a little asymmetry in one of the mirrors or beam splitters.[3]

If the two beams' optical path length differences are less than the light source's coherence length, interference fringes will result. The distance across which light waves retain their phase relationship is known as the coherence length.For constructive or destructive wave interference, interference fringes can arise even if the differences in the optical path lengths of the two beams are contained within the coherence length of the light source. In the interference pattern, these fringes appear as patterns of light and dark bars.[3]The extremely small coherence lengths of light sources allow for nearly equal optical path lengths for the two beams in the Mach-Zehnder interferometer, a feat that requires precise components and meticulous alignment. Maintaining the visibility and clarity of the interference fringes requires this level of accuracy.The sample's effect on the difference in optical path length can be assessed by inserting it into one of the beam paths. Changes in the interference fringe are observed to produce this measurement. These modifications offer vital details about the attributes and features of the sample under investigation. The Mach-Zehnder interferometer is an essential instrument for a wide range of scientific and technological applications because it can measure even minute variations in optical path length.[3] In physics history, the Michelson interferometer is particularly noteworthy.  Albert Michelson constructed it for use in the Michelson-Morley Experiment, which is among the most well-known physics experiments in history.  This experiment was supposed to measure variations in light speed as the earth went through space in order to identify the presence of luminiferous aether. In the same way that sound waves require air to exist, aether was believed to be a component of the universe, enabling light to pass through it. The existence of an aether was denied by Michelson and Morley, who were never able to measure any variation in the speed of light.[2]

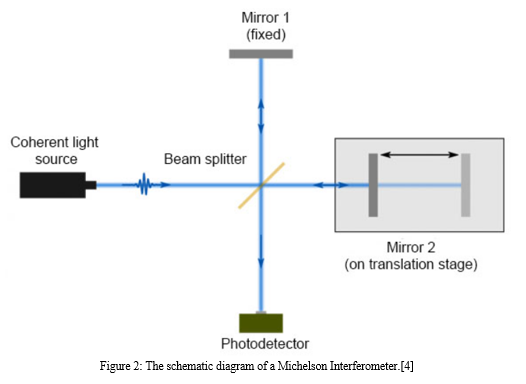
The discovery of gravitational waves by the LIGO experiment using a Michelson interferometer is the second reason the MI is so important.  As previously mentioned, the LIGO experiment allows us to detect gravitational wave activity.  Picture yourself in a forest, surrounded by a variety of plants, birds, and insects. Even though you can recognise them and can discern their patterns, you were unaware that you were wearing earplugs until someone removed them.  The sounds of the wind rustling through the leaves, the river you never knew existed, and the birds can all be heard now.  The LIGO experiment has opened our eyes to new directions in cosmic research, but that is the extent of its significance.[2]A precise instrument known as the Michelson interferometer divides a coherent light beam into two directions. Before these directions are once more combined to generate interference fringes, they follow distinct optical paths. It splits a light beam into two or more segments and also functions as a beam division interferometer. Beam splitter, compensating plate, and two mirrors make up the system. An American physicist named Albert A. Michelson created this amplitude-splitting apparatus in 1890. It is still a vital instrument in contemporary labs, where it is frequently used to measure minuscule distances, identify the wavelength of unknown light sources, and research the characteristics of optical medium.[4]

The Michelson interferometer is made up of three mirrors, which are shown in Figure 2: a compensating glass plate, a semi-transparent mirror called a beam splitter, and two highly polished mirrors called M1 that is fixed) and M2 is movable. The locations of M1 and M2 in relation to the beam splitter are distinct. The beam precisely reflects back along the path it originally travelled due to the precise alignment of the mirrors. Between the mirrors, at a 45° angle and parallel to one another, are the compensating glass plate and the beam splitter. Amplitude splitting is made possible by the beam splitter's opposing side, which is semi-silvered and consistently reflects and transmits light from the source.[4] Half of the light that enters the beam splitter is reflected back to the viewer by the mirror M1 through the beam splitter. The transmitted half of the original beam travels via the beam splitter in the direction of the observer, as shown in Figure 2, following its reflection back by the mirror, M2. Fringes are created when coherent beams interfere with one another, either destructively or constructively, during their recombination at the beam splitter.[4]

Two flat surfaces with partially reflected mirrors make up the Fabry-Perot interferometer. There may be relatively little space between the surfaces that are facing one another.  An FPI can occasionally be produced with a single glass slab that has somewhat reflective surfaces.[2] The beam divides on each reflection, transforming the FPI into a multiple beam interferometer.The ability to create extremely high resolution (much as a high number of lines/mm produces a high resolution diffraction grating) is one advantage of employing a multiple beam interferometer. A very clear interference pattern with a strong contrast between the light and dark fringes can be produced. FPI is used in many different contexts. The most popular method produces a laser with an exceptionally high quality factor Q by using a Fabry-Perot cavity.

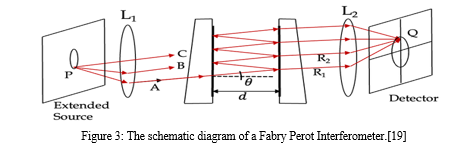
The multiple beam interference theory underpins the operation of the high-resolution Fabry-Perot Interferometer. numerous beam interference is the term used to describe the interaction of numerous coherent light beams that result in an interference pattern. It can be used to measure exact wavelengths, compare two extremely near wavelengths, calculate the refractive index of gases, calibrate standard metre scales based on wavelengths, and more [5].The two glass panels that make up the interferometer are parallel and extremely flat. They make a level space in the air between them. Eighty percent of the light is reflected by a glossy metal coating on the inside sides of the glass panes. The multiple reflections that occur between these plates are what enable the interferometer to function.[5] The interferometer employs glass plates with a range of thicknesses and angled outer surfaces relative to inner surfaces. This is done to make sure that there are no possible interference fringes on parallel, equally-inclined glass surfaces. A precise micrometre screw can be used to secure one plate and move the other. As a result, the air gap between the plates is reduced. A Fabry-Perot etalon is the name given to the device when both plates are immobile. In Figure 5, the Fabry-Perot interferometer configuration is displayed [5].

IV. APPLICATIONS OF INTERFEROMETERS IN SCIENCE AND ENGINEERING

In the optical industry, Newton (test plate) interferometry is often used to assess the quality of surfaces throughout the shaping and figuring process. A monochromatic light source illuminates the reference flats, which are resting with their bottom surfaces in contact with the test flats. A pattern of bright and dark bands is produced when the light waves reflected from both surfaces interfere with one another. Fabry-Pérot etalons are frequently used to regulate and monitor light wavelengths in spectroscopy, lasers, and telecommunications. Dichroic filters are etalons with many layers of thin film. Thin-film etalons are the filtering devices used in wavelength-division multiplexing, a technique in telecommunications that allows the use of several wavelengths of light across a single optical fibre. Etalons are used in single-mode lasers to suppress all optical cavity modes other than the one that is of interest [2].

A popular version of the Michelson interferometer for testing optical components is the Twyman–Green interferometer, created in 1916 by Twyman and Green.[6] The employment of a collimator and a monochromatic point light source are the primary features that set it apart from the Michelson arrangement. The Twyman-Green arrangement was criticised by Michelson (1918) for being inappropriate for testing big optical components because of the limited coherence length of the light sources that were available at the time. Michelson noted that the Twyman-Green was not useful for many applications because of geometric limits imposed by a restricted coherence length, which necessitated the use of a reference mirror of identical size to the test mirror.[7] Michelson's concerns were addressed decades later with the development of laser light sources. (A Laser Unequal Path Interferometer, or LUPI, is a Twyman–Green interferometer that uses a laser light source and an unequal path length.) . A diverging lens expands the light from a monochromatic point source before collimating it into a parallel beam. The focus of the lens being examined is aligned with the centre of curvature of a convex spherical mirror. An imaging device records the emergent beam for analysis.[8]

In integrated optical circuits, Mach-Zehnder interferometers are used to measure the relative phase variation between two externally modulated waveguide branches through light interference. The interference pattern will shift and a path difference will occur from a small tilt of one of the beam splitters. Mach-Zehnder interferometers serve as the foundation for many other kinds of electronics, including optical switches, sensors, and RF modulators[9, 10][11].The Thirty Metre Telescope and the Extremely big Telescope, two of the most recent proposed very big astronomical observatories, will have segmented designs. Hundreds of hexagon-shaped mirror segments will be used to construct their main mirrors. A significant problem lies in polishing and figuring these very aspheric and non-rotationally symmetric mirror pieces. Using a null corrector, a surface is compared to a spherical reference in traditional optical testing methods. Computer-generated holograms (CGHs) have started to be added to test settings for complicated aspheric surfaces in place of null correctors in recent years. The line spacing of real CGHs ranges from 1 to 10 μm. There is no wavefront alteration to the zero-order diffracted beam when laser light passes through the CGH. However, the first-order diffracted beam's wavefront is altered to conform to the test surface's intended shape. The first-order diffracted beam is directed towards the test surface in the shown Fizeau interferometer test setup, while the zero-order diffracted beam is directed towards the spherical reference surface. This arrangement allows the two reflected beams to combine to generate interference fringes. For the innermost mirrors, the identical test configuration can be utilised as for the outermost, with the exception of exchanging the CGH.[12]

Interferometers used in navigation systems include fibre optic gyroscopes (FOGs) and ring laser gyroscopes (RLGs). They function according to the Sagnac effect theory. RLGs and FOGs differ in that an external laser injects counter-propagating beams into an optical fibre ring; the system's rotation then creates a relative phase shift between those beams. In an RLG, the entire ring is part of the laser. The observed phase shift in a FOG is proportional to the angular velocity, whereas in an RLG it is related to the accumulated rotation [13].Heterodyning is a technique used in telecommunication networks to shift specific signal frequencies to separate channels that may share a single physical transmission line. The term for this is FDM, or frequency division multiplexing. For instance, 500 television channels can be carried simultaneously over a coaxial cable used by a cable television system because each channel is assigned a unique frequency to prevent interference. Transmitted and reflected beams are compared by continuous wave (CW) doppler radar detectors, which are essentially heterodyne detection instruments.[14] A method called holographic interferometry makes advantage of holography to track minute deformations in single-wavelength applications. It is utilised to detect greater surface flaws and perform dimensional metrology of large parts and assemblies in multi-wavelength systems.[2].Holographic interferometry was discovered by accident as a result of mistakes committed during the making of holograms. Early lasers were relatively weak and photographic plates were insensitive, necessitating long exposures during which vibrations or minute shifts might occur in the optical system. The resultant holograms, which showed the holographic subject covered with fringes, were considered ruined [15]. The Twyman–Green interferometers, which bear the names of Frank Twyman and Arthur Green, are optical surface characterization instruments. The Twyman–Green interferometer uses collimated beams that are enlarged to a significant diameter; otherwise, the optical configuration is comparable to that of a Michelson interferometer.

In the most basic scenario, an extended beam of this kind is directed straight into the surface under inspection, and the interference pattern that results is captured so that it can be viewed directly through an eyepiece or registered using a monochromatic electronic image sensor.[16]

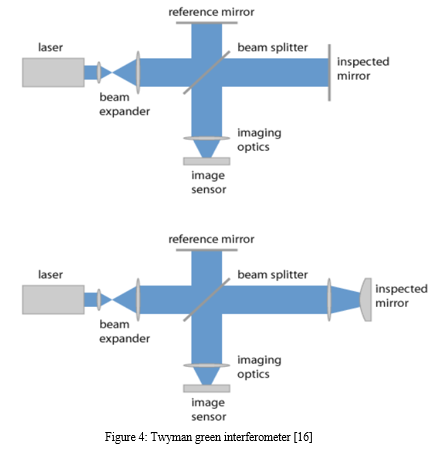
The surface under inspection may be a mirror or another type of optical device; to be used as an end mirror, the surface just needs to have a sufficient level of reflectivity; any greater reflection could contaminate the interference pattern. When paired with the right kind of mirror, some components (such as lenses, prisms, and mirror substrates) can also be placed in the beam path for gearbox inspection. For example, that can also be used with objectives for a microscope.[] The optical wavefronts must be roughly matched to the examined surface if it is not flat, for example, by utilising curved mirrors or one or more lenses. If not, the interference stripes that emerge could be too close together to be seen.[16]

Conclusion

As a conclusion, interferometry is a measurement technique that makes use of the wave interference phenomenon (typically light, radio, or sound waves). Certain properties of the waves themselves as well as the materials the waves interact with may be measured. Interferometers have a wide range of applications; they can measure anything from minute changes on a microscopic organism\'s surface to the composition of vast stretches of gas and dust in the far universe. More recently, they can even detect the nearly imperceptible motions caused by gravitational waves [20]. There are numerous practical uses for light interference, including in the fields of photonics and optics. Optical coatings, holography, laser interferometry, and spectroscopy are a few instances. Additionally, it finds use in fields including microscopy, metrology, and telecommunications [21].

References

[1] https://www.renishaw.com/en/interferometry-explained--7854 [2] https://www.opticsforhire.com/blog/interferometers-types-performance-design-considerations/ [3] https://www.gophotonics.com/community/what-is-a-mach-zehnder-interferometer [4] https://www.gophotonics.com/community/what-is-a-michelson-interferometer [5] https://www.gophotonics.com/community/what-is-a-fabry-perot-interferometer [6] Malacara, D. (2007). \"Twyman–Green Interferometer\". Optical Shop Testing. pp. 46–96. doi:10.1002/9780470135976.ch2. ISBN 978-0-470-13597-6. [7] Michelson, A. A. (1918). \"On the Correction of Optical Surfaces\". Proceedings of the National Academy of Sciences of the United States of America. 4 (7): 210–212. Bibcode:1918PNAS....4..210M. doi:10.1073/pnas.4.7.210. PMC 1091444. PMID 16576300. [8] Interferential Devices – Twyman–Green Interferometer\". OPI – Optique pour l\'Ingénieur. Retrieved 4 April 2012. [9] Heideman, R. G.; Kooyman, R. P. H.; Greve, J. (1993). \"Performance of a highly sensitive optical waveguide Mach–Zehnder interferometer immunosensor\". Sensors and Actuators B: Chemical. 10 (3): 209–217. CiteSeerX 10.1.1.556.5526. doi:10.1016/0925-4005(93)87008-D [10] Oliver, W. D.; Yu, Y.; Lee, J. C.; Berggren, K. K.; Levitov, L. S.; Orlando, T. P. (2005). \"Mach–Zehnder Interferometry in a Strongly Driven Superconducting Qubit\". Science. 310 (5754): 1653–1657. arXiv:cond-mat/0512691. Bibcode:2005Sci...310.1653O. doi:10.1126/science.1119678. PMID 16282527. S2CID 46509116 [11] Nieradko, ?.; Gorecki, C.; JóZwik, M.; Sabac, A.; Hoffmann, R.; Bertz, A. (2006). \"Fabrication and optical packaging of an integrated Mach–Zehnder interferometer on top of a movable micromirror\". Journal of Micro/Nanolithography, MEMS, and MOEMS. 5 (2): 023009. Bibcode:2006JMM&M...5b3009N. doi:10.1117/1.2203366 [12] Burge, J. H.; Zhao, C.; Dubin, M. (2010). \"Measurement of aspheric mirror segments using Fizeau interferometry with CGH correction\" (PDF). Proceedings of SPIE. Modern Technologies in Space- and Ground-based Telescopes and Instrumentation. 7739: 773902. Bibcode:2010SPIE.7739E..02B. doi:10.1117/12.857816. S2CID 49323922 [13] Anderson, R.; Bilger, H.R.; Stedman, G.E. (1994). \"\"Sagnac effect\" A century of Earth-rotated interferometers\" (PDF). Am. J. Phys. 62 (11): 975–985. Bibcode:1994AmJPh..62..975A. doi:10.1119/1.17656. Retrieved 30 March 2012. [14] Golio, Mike (2007). RF and Microwave Applications and Systems. CRC Press. pp. 14.1–14.17. ISBN 978-0-8493-7219-3. Retrieved 27 June 2012. [15] Holographic interferometry\". Oquagen. 2008. Retrieved 22 May 2012. [16] https://www.rp-photonics.com/twyman_green_interferometers.html [17] https://commons.m.wikimedia.org/wiki/File:Mach-Zehnder_interferometer%2Bportlabels.svg [18] Hariharan, P. (2007). Basics of Interferometry. Elsevier Inc. ISBN 978-0-12-373589-8. [19] http://www.physicsbootcamp.org/section-fabry-perot-interferometer.html [20] https://www.ligo.caltech.edu/page/what-is-interferometer [21] https://www.adda247.com/school/interference-of-light/

Copyright

Copyright © 2024 Muhammad Arif Bin Jalil. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.