Loan Repayment Ability Using Machine Learning

Abstract

Loan lending has risen quickly around the world in recent years. The fundamental goal of loan lending is to eliminate intermediaries such as banks. Loan lending is a fantastic option to apply for a loan for a small business or an individual who does not have enough credit or a credit history. However, the basic issue with loan lending is information asymmetry in this paradigm, which may not accurately predict lending default risk. Lenders solely decide whether or not to finance the loan based on the information supplied by borrowers, resulting in imbalanced datasets containing uneven completely paid and default loans. Unfortunately, the unbalanced data are hostile to traditional machine learning approaches. In our case, models with no adaptive strategies would concentrate on learning the standard payback. However, the minority class\'s characteristics are crucial in the lending sector. We use re-sampling and cost-sensitive procedures to analyse unbalanced datasets in this work, in addition to multiple machine learning schemes for forecasting the default risk of loan lending. Furthermore, we validate our suggested strategy using Lending Club datasets. The experiment findings suggest that our proposed technique may effectively improve default risk prediction accuracy.

Introduction

I. INTRODUCTION

Loan lending (loan lending) was invented in 2005, and it has lately gained in popularity throughout the world. loan lending is a method of obtaining credit without the involvement of a financial entity, such as a bank, in the selection phase, and offers the potential to obtain better terms than the typical banking system [1]. loan lending also provides an internet platform for directly connecting borrowers and lenders.

Due to the elimination of brick-and-mortar operational costs, loan lending may offer borrowers lower interest rates than banks. As a result, loan financing is an option for small enterprises and certain people with no credit history.

However, asymmetric information becomes a basic issue in loan lending since lenders only make loan decisions based on information given by borrowers.

Normally, the dataset for loan lending is unbalanced since completely paid and default loans are not equal. In our dataset, the ratio of completely paid to default loans is roughly 3.5:1. There are different unbalanced datasets in the real world, such as fraud prevention, risk assessment, medical diagnosis, and so on. As a result, making a prediction on such an unbalanced dataset is problematic since classifiers are prone to recognising the majority class rather than the minority class. As a result, the classification's output will be skewed. In this scenario, resolving the issue in the categorization of the unbalanced dataset is critical. To deal with the unbalanced dataset, this work employs undersampling and cost-sensitive learning. Meanwhile, for machine learning techniques, we use logistic regression, random forest, and neural network to predict loan lending default risk. This document is also arranged as follows: Section 2 provides a brief overview of related work on estimating default risk in loanlending and categorization of imbalance datasets. Section 3 follows, and it describes our approaches. Section 4 then displays the performance measures and experiment results. The final one is the conclusions reached in Section 5.

II. RELATED WORKS

A. Credit Risk

Credit risk is the most essential topic in the financial world, and there are several sorts of credit risk study. Odom and Sharda [2] examined the neural networks model with the discriminant analysis approach in predicting bankruptcy risk. The results then shown that the convolutional neural model had a greater percentage than the discriminat analysis approach. Atiya [3] evaluated the issues of predictive modelling using neural networks and presented unique inputs taken from stock markets as new indications to significantly enhance prediction. Furthermore, Emekter et al. [4] discovered that higher interest rates imposed to high-risk borrowers were inadequate to compensate for the increased possibility of loan failure.

The Lending Club must figure out how to attract borrowers with high FICO scores and high wages in order to fund their organisations. Meanwhile, in loan lending, Bachmann et al. [1] and Mateescu [5] evaluated the history of loan lending and analysed its benefits and drawbacks.

They then discussed how loan lending works and the distinction between typical bank lending and loan lending. Serrano-Cinca et al. [6] examined numerous variables in loan lending default risk prediction using statistical approaches such as Pearson's correlation, point-biserial correlation, and the chisquare test.

They developed 7 logistic regression models with distinct 7 variables to evaluate the greatest predictive factor of default. Aside from the statistical strategy, some studies employed machine learning methods to estimate default risk. Jin and Zhu [7] evaluated three types of machine learning models in loan lending default risk prediction: decision trees, neural networks, and support vector machines. They utilised the Lending Club dataset from July 2007 to December 2011 and deleted loan data with the status "current." The forecast result was divided into three categories: "defaulter," "require attention," and "well paid." The average percent hit ratio (precision) and life curve were then used to evaluate performance.

Byanjankar et al. [8] created a neural network model using datasets from the loan lending platform Bondora and evaluated performance using the confusion matrix and accuracy. The authors of [9] presented a profit scoring method in 2016. Credit rating systems in [9] are mostly concerned with loan default likelihood. The findings of studying borrower interest rates and lender profitability show that loan lending is not a trend in the present market. The method described in reference [10] combines cost-sensitive learning and severe gradient boosting.

As a result, this strategy can reduce an optimization issue to integer linear programming. Unlike previous research, this study assesses predicted profitability in other criteria, such as annualised rate of return (ARR). The metrics employed in estimate are based on an unbalanced dataset. Although there have been some studies on predicting loan default risk, they have not addressed the issue that unbalanced datasets present. Their primary assessment criteria was accuracy, which proved inappropriate for unbalanced datasets.

B. Classification with Imbalanced Datasets

Extremely unbalanced datasets are an exception to order issue since the class dispersion is not equal among the classes. In unbalanced datasets, there are usually two classes: the bulk of negatives and the minority of positives. These types of data offer a problem for data mining since traditional classification methods need a balanced training set, which implies a bias it toward the dominant (negative) class [11].

For example, we have a classifier that is 96 percent accurate. It appears to be extremely excellent, however if the 96 percent data is classifier data, classifiers will always forecast the class membership in order to achieve high accuracy.Veni et al. [12] discovered why conventional classification algorithms perform poorly in unbalanced samples. For starters, these algorithms are focused on precision. The second assumption is that the incidence of all classes is uniform. The final point is that various classes have the same mistake cost. To address the issue of anticipating unbalanced datasets, they provided sampling techniques and cost sensitive learning, as well as additional performance measures that were better suited for outlier detection, such as confusion matrix, accuracy, F1-score, and so on. In addition, Chawla [13] observed the artificial minority upsampling approach (SMOTE), ensemble-based method, and SMOTE Boost method on unbalanced datasets to improve sampling methods. Additionally, Chawla et al. [14] reviewed the topic of unbalanced datasets and other researchers' solutions to it.

III. PROPOSED SCHEME

This section describes the path toward building advance default expectation models, as seen in Fig. 1.

A. Pre-processing

Many characteristics in the loan lending databases are empty for the majority of entries. As a result, we remove these properties and change the nominal features using a one-hotencoding strategy that may turn nominal features into a classification-ready format. For example, we have a feature called "purpose of the loan," which contains string values like "Car," "Business," and "Wedding." Ordinal value is typically used to encode them as integers such as 0, 1, and 2. Different categories, however, have the same weight in machine learning algorithms. As a result, the ordinal technique cannot be used in machine learning since the lowest and highest values would influence the classification outcome. One-hot encoding employs a single Boolean column with a distinct weight for each category.

Finally, we employ feature scaling to normalise each feature's value range.

The effectiveness of machine learning methods will be influenced if certain characteristics have a large range of values. Furthermore, feature scaling accelerates gradient descent convergence.

B. Feature Selection

This section describes the features that are employed in prediction. First, we choose relevant features intuitively, such as loan amount, instalment, and so on. Table 1 displays the important characteristics. Second, we differentiate borrowers' addresses based on their three-digit zip code. If we use one-hot encoding to encode the zip code, the data sizes will be too large. As a result, we opt to compute the mean and median income for each state and incorporate these two variables into the data. Words that characterise loan applications appear in original characteristics. Words, in general, cannot have numerical properties. First, we examine the terms. Two word clouds clearly depict various frequent terms, such as "credit," "card," and "loan." That is, popular terms are found in both positive and negative samples. These popular terms might result in decreased accuracy in categorization works. As a result, we delete frequent terms from our features. Finally, we converted the remaining words to numerical characteristics.

C. Re-Sampling

By modifying the distribution class, the re-sampling procedure balances the datasets. It is classified into two categories. The first is under-sampling, which causes the bigger class to shrink to the size of the smaller class. Meanwhile, the second kind is over-sampling, which causes the tiny class to grow to a size comparable to the bigger class [15].

1. Under-Sampling

To balance the datasets, pick a subsample of the class label whose size equals the set of minority class. However, it may pose another problem since it deletes some vital data. Another sort of under-sampling approach is random under-sampling, which removes data from the majority class at random until the class distribution balances. In our study, we used Tomek as an under-sampling strategy. Under-sampling can also be accomplished via Tomek linkages. Tomek linkages are also thought of as a set of the closest neighbours of opposite class with the shortest distance. Tomek link technique removes data from the class label that corresponds to Tomek link during under-sampling. Tomek linkages are also thought of as a pair of the closest neighbours of opposite class with the shortest distance. Tomek link technique removes data from the class label that corresponds to Tomek link during under-sampling.Tomek linkages are also thought of as a pair of the closest neighbours of opposite class with the shortest distance. Tomek link technique removes data from the class label that corresponds to Tomek link during under-sampling.

2. Over-Sampling

To balance the distribution of the datasets, the over-sampling approach generates additional data from the minority class. The random over-sampling approach is a straightforward way to increase the size of minority data points by randomly replicating it.

Another approach for doing oversampling is SMOTE [16], which means for simulated minority oversampling technique. Take a minority example feature vector xi, and m is the nearest neighbour minority example in feature space. Then, mediation between m and xi is used to generate fresh minority class data until distribution balance is achieved. Borderline SMOTE is a novel variation of the SMOTE over-sampling approach that exclusively over-samples data from the minority class [17].If the number of xi's nearest neighbours who are members of the majority class and fit , define the near the boundary and create new data.

3. Cost-Sensitive Learning

In practise, the ratio of positive to negative samples is not 1:1. For example, the number of murderers would be lower than the number of good individuals. Loan data is also unbalanced. As a result, the standard cost function would incur from skewed data. To get around this, we use a scalar in Eq. 1. As a result of fewer negative samples, the term behind the addition operator would rise. In this study, we do experiments with values ranging from 1 to 4.8. In comparison to previous strategies for dealing with unbalanced datasets, Eq. 1 offers a straightforward strategy for machine learning models with skewed datasets. As a result, the model can categorise the targets superior than one that does not include the adjustable cost function.

where h is an activation function, such as sigmoid function.

4. Machine Learning Scheme

We present the notion of cost-sensitive learning in section III-C3. Following that, we will demonstrate the machine learning models used in this work. Simultaneously, the logistic regression's cost function is changed by Eq. (1) Random forest and neural networks require re-sampling.

a. Logistic Regression: This section discusses the machine learning models used in this investigation. First, we employ logistic regression, which is appropriate for binary categorization. Eq. (2) depicts the logistic regression model, which converts linear regression to non-linear regression. The logistic regression model produces probabilities ranging from 0 to 1. The logistic regression limit is normally set at 0.5. If the result is larger than 0.5, it is anticipated to be the genuine value. In this study, we used Eq. 1 to develop our training technique. The scikit learn framework sets the other arguments to default settings.

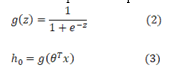
b. Random Forest: The following machine learning technique is random forest (RF), which is an array of decision trees as seen in Fig. 4. It builds a large number of decision trees during training and generates a variety of models by bagging data sets and randomly selecting features. Finally, the final decision is determined by majority voting. To construct the random forest trees, we use the CART (classification and regression trees) approach. The CART method is a linear decision tree that measures impurities using the Gini index.

c. Neural Networks: Biological neural networks inspire neural networks. Figure 5 depicts a simple three-layer neural network. The input layer connects with one or more convolutional nodes and passes various characteristics. The node is known as a neuron, and it has an activation function. Every link carries a hefty burden. The weight value varies from one to the next. These weights as well as the non-linear activation function create complicated relationships In our work, the model has 64 input neurons, two hidden layers, and one output. At avoid our model from classifiers, we set the dropout rate to 0.5.

IV. RESULTS AND DISCUSSION

A. Evaluation Metrics

To assess unbalanced datasets, accuracy alone is insufficient. As a result, we employ another assessment metric known as the confusion matrix to assess the efficacy of machine learning techniques. As shown in Fig. 6, the confusion matrix is a special table arrangement that may display the classifier result. Classifiers that predict correctness are known as TP (true positive) and TN (true negative). Meanwhile, classifiers that predict incorrectness are referred to as FP (false positive) and FN (false negative). The recall representative is therefore termed sensitivity since it predicts the positive rate in all real positive data, but the precision representative is the accurate rate when it forecasts positive.The true negative rate is another name for specificity. We employ the F1-score, which is the geometric mean of precision and recall, and the G-mean, which combines sensitivity and accuracy, to integrate recall and precision.

B. Lending Club Datasets

We utilise the Lending Club databases, which comprise 887,379 loan records and were gathered from 2007 to 2015. This information was obtained from the website https://www.lendingclub.com/investing. The loans data with the status "Current" are then removed, leaving 269,668 loans data, as shown in Fig. 7. The condition of all loans in the dataset is depicted in Fig. 8. We distribute 70% of the data for training (N = 188,767) and 30% of the data for testing (80,901).

Each record in the raw data has 73 characteristics. Following that, we divide the debt data into two categories: default and completely paid. Default labels have values such as default, charge off, and late payment loans, which are categorised as positive instances, whereas completely paid labels are classified as negative examples. In our dataset, the ratio of completely paid to default loans is roughly 3.5:1.

The F1-score is 15.606 while utilising the original data, however when we try to balance the dataset by using other sampling strategies, the F1-score rises. The same phenomenon applies with neural networks and logistic regression, the results of which are shown in Tables 3 and 4. Tables 2, 3, and 4 clearly show that logistic regression with re-sampling or cost-sensitive learning beats random forest and neural networks. Based on the results, random under-sampling is the best sampling technique since it has the greatest F1-score of any sample method. Table 5 also illustrates the outcome of logistic regression with available resources training. We evaluated 20 various values and discovered that the best are 3, 3.2, and 3.4 since the accuracy and precision default varied somewhat. The number of features used to achieve optimal performance is an essential consideration in feature selection. As a result, we execute random forest to choose the first 10 key traits that are yield.

Furthermore, we experiment with the randomized under-sampling strategy using another feature set that only includes the first three critical traits, as shown in Table 6.Furthermore, we pick two loan amount ranges to investigate the link between predicting outcomes and amount distribution. The first loan is for less than $5,000, while the second is for more than $30,000. Tables 7 and 8 illustrate the outcomes. Overall, the results of two loan amount dispersal range data are not significantly different from the results of complete data. It indicates that the loan amount has little effect on the forecasted result. Overall, in this study, costsensitive learning and re-sampling increase prediction task quality. Random under-sampling, in particular, can effectively help machine learning models achieve better outcomes than original ones.

Conclusion

Loan lending is a method of lending money that does not involve banking firms and allows borrowers to interact directly with lenders. However, P2P lending suffers from a basic difficulty due to an uneven dataset. As a result, classifiers are more likely to favour the majority over the minority. In this paper, we use dimensionality reduction techniques and cost-sensitive mechanisms to analyse unbalanced datasets, as well as a variety of machine learning algorithms to estimate the default risk of P2P lending. To validate our suggested strategy, we obtain the dataset from Lending Club. In the experiment findings, random under-sampling outperforms all other classifiers. The suggested approach may therefore effectively enhance the predictive performance for default risk after pre-processing and feature selection.

Copyright

Copyright © 2022 Suyog Nemade. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.