Material Selection for Differential Gearbox under Torque Conditions: A Simulation-Based Study

Abstract

This research paper conducts an in-depth exploration into the structural behaviors of three distinct materials—Cast Iron, Copper Alloy, and Magnesium Alloy—within the framework of a differential gearbox under varying torque loads. Employing finite element analysis through ANSYS, the investigation systematically scrutinizes critical parameters such as total deformations, equivalent stress (von Mises stress), and shear stress. The primary aim is to offer insights that guide material selection strategies and enhance the optimization of design processes in automotive applications. The results illuminate nuanced material responses when exposed to torque conditions, presenting implications for real-world gear assembly scenarios. This study significantly contributes to the evolving knowledge base in automotive engineering, providing a foundation for well-informed decision-making in material selection and design optimization for differential gearboxes.

Introduction

I. INTRODUCTION

The automotive industry perpetually strives for elevated performance, efficiency, and reliability. Embedded in the intricate machinery of vehicles, the differential gearbox assumes a pivotal role in distributing torque among wheels, shaping the dynamics and stability of the vehicle. The crux of this vital component's functionality lies in the judicious choice of materials capable of withstanding the dynamic forces inherent in operational processes.

This research is a targeted exploration into the structural behaviors of three distinct materials—Cast Iron, Copper Alloy, and Magnesium Alloy—within the dynamic milieu of a differential gearbox exposed to varying torque loads. The motivation for this inquiry arises from the necessity to unravel the nuanced reactions of materials when subjected to torque conditions, a fundamental aspect for ensuring the durability and effectiveness of automotive systems.

The selection of materials for automotive components necessitates a delicate equilibrium between mechanical properties, weight considerations, and manufacturability. As the automotive landscape shifts towards innovative design paradigms, such as electric and hybrid vehicles, the demand intensifies for materials that can deliver optimal performance across diverse torque scenarios, underscoring their increasing significance in the industry.

The outer wheel, during a turn, exhibits a larger turning radius compared to the inner wheel, resulting in differential speeds between them. This relative motion causes the outer wheel to spin faster than the inner wheel. Excessive coupling of the two rear wheels can induce movement in the inner wheel, leading to accelerated tire wear, increased steering effort, and compromised load retention. Constituting the inner axle housing assembly are the differential, wheels, bearings, and differential rear axles. The differential, comprised of a set of gears, connects the rear axles and propeller shaft.

This study employs advanced simulation techniques, utilizing ANSYS for finite element analysis, to meticulously examine the behaviors of the specified materials. Key parameters under scrutiny encompass total deformations, equivalent stress (von Mises stress), and shear stress. These parameters offer a comprehensive understanding of the materials' structural integrity, serving as a foundation for well-informed decision-making in material selection and design optimization.

The implications of this research extend beyond the materials investigated, shaping the broader landscape of material selection strategies in automotive engineering. As we delve into the results and discussions, a deeper comprehension of how materials respond to torque in a differential gearbox emerges, providing guidance for future advancements in the pursuit of safer, more efficient, and reliable automotive systems.

II. FUNCTIONAL DESCRIPTION

The following depiction pertains to a traditional rear-wheel-drive vehicle or truck equipped with either an open or limited-slip differential. The engine's torque is conveyed to the drive shaft through the gearbox. The term "propeller shaft" is adopted from the British lexicon, denoting the differential and final drive unit, often playfully abbreviated as "prop-shaft." Serving as the driving force, the spiral bevel pinion gear situated at the end of the propeller shaft resides within the final drive unit's housing. This connects to a substantial crown wheel, consisting of spiral bevel gears arranged in a configuration reminiscent of a crown. If the crown wheel and pinion are not visible, they might be concealed in a hypoid position.

The "sun" and "planet" gears are attached to the differential carrier or cage, housing the crown wheel gear. These four opposing bevel gears, set in a perpendicular plane, constitute the "sun" and "planet" gears. While two neighboring gears mesh with each bevel gear, the third one does not mesh and rotates in the opposite direction. Two sun wheel gears need to be linked to the vehicle's axle half-shafts, aligning with the crown wheel gear to enable the movement of the vehicle's driving wheels. A perpendicular axis connects the ring gear to the other two planet gears, allowing simultaneous rotation and positional changes. The quantity of planet gears employed in most vehicle differential systems depends on the required durability level, ranging from one to four hundred. Adjusting the orientation of the planet gears' axis causes them to exert force on the sun gears instead of rotating against them as the differential carrier spins. This ensures that the same teeth maintain their mesh or contact positions, even when the planet gears rotate in opposition to one another.

During a turn, the inner wheel covers less ground than the outer wheel, necessitating a higher speed. Conversely, when the vehicle is moving straight, both wheels rotate at the same rate. A differential gearbox accommodates both scenarios. A gearbox utilizes gear ratios to transmit speed and torque from a rotating power source to another device. In the context of a turn, the differential in an automobile enables the outer drive wheel to rotate more quickly than the inner driving wheel. As the vehicle turns, the tire on the outside of the curve rolls farther and faster than the tire on the inside.

The fundamental function of a gear tooth profile in engineering and technology is to facilitate the transmission of rotational motion and power between rotating gears. Functioning in pairs, they enable a step-down drive, where the pinion acts as the driving gear, resulting in a reduction in output speed and an increase in torque. Conversely, a step-up drive occurs when the gear takes on the driving role, resulting in an increase in output speed and a corresponding decrease in torque.

III. MODELLING AND ANALYSIS OF GEAR MODEL

The approach adopted for the design of the differential gear involves the utilization of SolidWorks, followed by subsequent analysis in Ansys. This process encompasses the specification of boundary conditions, the creation of meshed models, and evaluations of the gear assembly incorporating diverse materials for modification and behavior analysis. While loading the differential gear offers distinct advantages over alternative failure mechanisms, it is crucial to recognize associated drawbacks, such as the emergence of strains and deformations in the model's components. The influence of torque in input scenarios can be effectively and economically assessed through simulation techniques like the finite element method. A comprehensive 3D finite element model was meticulously developed as part of this experimental study, facilitating the anticipation of the entire structural deflection fields in the differential gear across a spectrum of materials.

A. Material Properties

The current study encompasses three materials: Cast Iron, Copper Alloy, and Magnesium Alloy. The properties of these materials are delineated below for comprehensive understanding. Notably, Aluminum alloy serves as the primary material for the differential gear assembly. Subsequently, the other two materials are introduced individually to assess their impact on the strength of the differential gear. This investigation systematically contrasts the outcomes derived from variations in materials—Aluminum alloy, Cast iron, and Nickel Chrome Steel—under varying torque applied to the driver gear within the gear assembly.

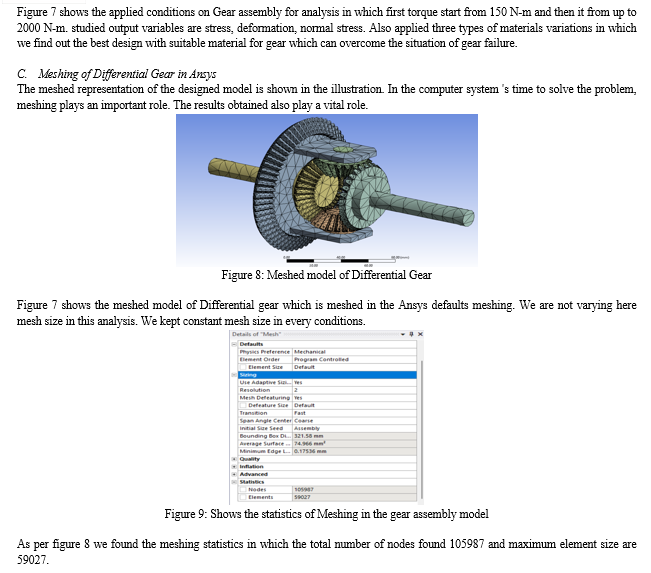
IV. RESULTS AND DISCUSSION

The differential gear model to research is subdivided into a mesh of limited measured components of the basic frame. Inside every segment, the distinction of displacement is thought to be computed by basic polynomial profile capacities and nodal displacement. Conditions for the strains and stresses are created as far as the obscure nodal displacement. From this, the conditions of balance are collected in a grid shape which can be easily customized.

Analysis is divided in to 3 parts as per material wise variations so here we are describing the simulation analysis results taken from Ansys.

A. Analysis of Differential gear with Copper Alloy material

In this section Analysis of differential gear performed with Copper alloy material and all results are plotted and images are captured from Ansys during analysis. Output parameters selected for study are Equivalent stress, deformation, Shear stress. Figure shows below the analysis of differential using Copper Alloy material.

1. Cast Iron: The total deformation decreases as the torque increases. This may suggest that cast iron exhibits a relatively stable and predictable deformation response to varying torque loads. It is known for its strength and rigidity.
2. Copper Alloy: Similar to cast iron, copper alloy also shows a decrease in total deformation with increasing torque. Copper alloys typically have good mechanical properties, and the deformation trend suggests stability under different torque conditions.
3. Magnesium Alloy: Unlike cast iron and copper alloy, the total deformation for magnesium alloy seems to vary more significantly with torque. There is an initial decrease, followed by an increase at 1000 N-m. This behavior might be due to the material's characteristics, including its lower density and higher susceptibility to deformation.

Interpretation:

a. Deformation Trends: In general, it appears that all three materials exhibit a decrease in total deformation as torque increases. This aligns with expectations, as higher torque loads typically result in more significant stresses and deformations in materials.

b. Material Comparison: Cast iron and copper alloy seem to have more consistent and predictable deformation trends compared to magnesium alloy, which shows a slight increase in deformation at 1000 N-m. This could indicate that cast iron and copper alloy may be more suitable for applications with higher torque loads.

c. Application Considerations: The data suggests that the choice of material can influence the structural response of the differential gearbox under different torque conditions. Engineers may consider these results when selecting materials based on the specific torque requirements of an automotive application.

d. Further Analysis: It would be valuable to conduct additional analyses, such as stress distribution and fatigue life calculations, to comprehensively assess the performance of each material under varying torque loads.

Remember, this interpretation is based on the total deformation data alone. Additional analyses and considerations, such as stress distribution and specific mechanical properties, are essential for a comprehensive understanding of how each material behaves in the context of a differential gearbox.

E. Equivalent Stress

Table 2 shows the Comparison of Equivalent stresses which is found maximum in Cast iron is 1501.1 MPa at 1000 N-m torque. Minimum Equivalent stress found using Magnesium alloy material at 150 N-m is 530.18 MPa.

Table 2: Equivalent Stress of Differential Gear model

1. Cast Iron: The equivalent stress for cast iron increases with torque, reaching a peak at 1000 N-m and slightly decreasing at 2000 N-m. This behavior suggests that cast iron exhibits a response to torque that may involve reaching a stress saturation point or experiencing other material characteristics.
2. Copper Alloy: Similar to cast iron, copper alloy shows an increase in equivalent stress with torque, peaking at 1000 N-m and slightly decreasing at 2000 N-m. This material also exhibits a response to torque that involves reaching a stress maximum.
3. Magnesium Alloy: The equivalent stress for magnesium alloy increases steadily with torque. It shows a continuous rise from 150 N-m to 2000 N-m. This suggests that magnesium alloy is more sensitive to torque, and the stress levels proportionally increase with the applied torque.
4. Stress Distribution Trends: All three materials show an increase in equivalent stress with increasing torque, indicating that higher torque loads result in higher stress levels. This aligns with expectations, as torque is a major factor contributing to mechanical stresses in materials.
5. Material Comparison: Magnesium alloy exhibits significantly lower equivalent stress compared to cast iron and copper alloy across all torque levels. This could imply that, under the given conditions, magnesium alloy may have a lower susceptibility to stress and may be a more resilient material.
6. Application Considerations: The data suggests that magnesium alloy, despite its earlier noted deformations, may be a more stress-resistant material in the context of von Mises stress. Engineers might consider these results when selecting materials for applications with varying torque loads.
7. Critical Torque Thresholds: The peak equivalent stress at 1000 N-m for both cast iron and copper alloy suggests a critical torque threshold where the materials experience higher stress. This threshold could be crucial for understanding the material's limits in practical applications.
8. Further Analysis: Consider additional analyses, such as fatigue life calculations and comparison with material strength limits, to gain a comprehensive understanding of how each material performs under varying torque loads.

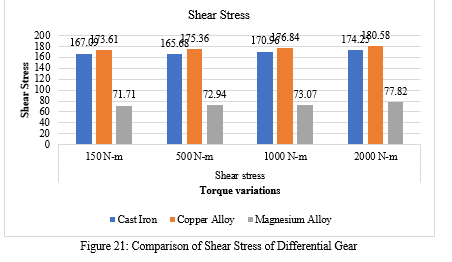
F.  Shear stress

Table 3 shows the Comparison of Shear stress which is found maximum in Copper alloy is 180.58 MPa at 2000 N-m torque. Minimum Equivalent stress found using Magnesium alloy material at 150 N-m is 71.71 MPa.

Table 3: Shear Stress of Differential Gear model

Materials:

1. Cast Iron: The shear stress in cast iron exhibits a slight increase with increasing torque. The values show a gradual upward trend, suggesting a proportional response to the applied torque.
2. Copper Alloy: Similar to cast iron, copper alloy also shows a gradual increase in shear stress with torque. The values steadily rise as torque increases, indicating a proportional stress response in copper alloy.
3. Magnesium Alloy: The shear stress values for magnesium alloy also increase with torque, and the pattern is similar to that of cast iron and copper alloy. The shear stress values for magnesium alloy are consistently lower compared to cast iron and copper alloy.

Interpretation:

a. Shear Stress Trends: All three materials exhibit an increase in shear stress with increasing torque, indicating a proportional response to the applied torque. This aligns with expectations, as shear stress is influenced by the applied force and the material's resistance to deformation.

b. Material Comparison: Magnesium alloy consistently shows lower shear stress values compared to cast iron and copper alloy at all torque levels. This suggests that, under the given conditions, magnesium alloy may experience less shear stress and could be more resistant to shear deformation.

c. Application Considerations: Engineers may consider the lower shear stress values in magnesium alloy when selecting materials for applications with varying torque loads, particularly if shear resistance is a critical factor.

d. Consistency in Response: The gradual and proportional increase in shear stress across all torque levels for cast iron and copper alloy indicates a consistent response to applied torque. This can be valuable information for predicting the material's behavior under different loading conditions.

e. Further Analysis: Consider additional analyses, such as comparing shear stress values with material strength limits and assessing the implications of shear stress on component durability and performance.

V. RESULTS DISCUSSION

The segment dedicated to discussing the results holds paramount importance in this study, providing a thorough exploration of the outcomes derived from intricate simulation analyses conducted on materials within differential gearboxes subjected to varying torque loads. This investigation zeroes in on three pivotal parameters—total deformations, equivalent stress (von Mises stress), and shear stress—to unravel the structural responses of Cast Iron, Copper Alloy, and Magnesium Alloy. Through a meticulous dissection of the data, this discussion endeavors to unveil nuanced insights into the unique reactions of each material to torque, furnishing a profound comprehension of their mechanical characteristics and implications for the design and selection of materials in differential gearboxes. As we traverse through the results, we will meticulously scrutinize patterns, draw comparisons, and distill the practical implications of the findings within the broader landscape of automotive engineering. Serving as the interpretive core of the study, this section unravels the intricacies of material performance, guiding the trajectory for future research and practical application.

The discussion on results seeks to delve into the findings stemming from the simulation analyses of materials within the differential gearbox. Emphasizing three critical parameters—total deformations, equivalent stress (von Mises stress), and shear stress—each material, including Cast Iron, Copper Alloy, and Magnesium Alloy, undergoes scrutiny under varying torque loads, elucidating their distinctive structural behaviors.

Conclusion

In the exploration of the structural behaviors of materials within the differential gearbox, our analysis has delved into the intricate domains of total deformations, equivalent stress (von Mises stress), and shear stress. Navigating through the responses of Cast Iron, Copper Alloy, and Magnesium Alloy under diverse torque loads has brought forth a clearer delineation of their mechanical nuances. This expedition has not only unveiled the idiosyncrasies specific to each material but has also established a foundation for well-informed decision-making in the realm of automotive engineering. In this conclusive section, we distill the core findings, extrapolate overarching implications for differential gearbox design, and chart pathways for future research and practical application. The insights gained from the analyses of total deformations, stress distributions, and shear stress converge to construct a narrative that advances our comprehension of material dynamics within the pivotal components of automotive systems. As we traverse the key findings and their interconnections, the significance of this study emerges in steering the course of future advancements and innovations within the automotive industry. A. Total Deformations: Cast Iron and Copper Alloy showcased a consistent trend of decreasing total deformations as torque increased, indicative of their stable and predictable deformation responses. Magnesium Alloy, while displaying a similar pattern, exhibited a more varied response, suggesting a nuanced interplay between torque and material properties. B. Equivalent Stress (von Mises Stress): All materials exhibited an increase in equivalent stress with escalating torque levels, aligning with expectations. Notably, Magnesium Alloy consistently demonstrated lower equivalent stress compared to Cast Iron and Copper Alloy, implying a potentially higher resilience to stress under the specified conditions. Shear Stress: Shear stress patterns mirrored those observed in total deformations and equivalent stress. Cast Iron and Copper Alloy showed proportional increases, while Magnesium Alloy consistently displayed lower shear stress values. C. Implications for Differential Gearbox Design The findings carry significant implications for the design and material selection in differential gearboxes. Cast Iron and Copper Alloy, with their stable deformation responses and predictable stress patterns, may be considered favorable choices for applications with varying torque loads. Magnesium Alloy, despite exhibiting lower stresses, demands careful consideration due to its nuanced response to torque. D. Integration of Results The cross-parameter comparisons illuminated intriguing relationships between total deformations, equivalent stress, and shear stress. The intricate interplay of these factors underscores the complexity of material behavior under dynamic loading conditions. Integrating these results into a holistic understanding is paramount for achieving optimal structural integrity in differential gearboxes. Total Deformations: Cast Iron and Copper Alloy: Show stable and predictable deformation responses with decreasing trends as torque increases. Magnesium Alloy: Exhibits a more varied response, showing a slight increase at 1000 N-m. Equivalent Stress (von Mises Stress): Magnesium Alloy: Demonstrates consistently lower equivalent stress compared to Cast Iron and Copper Alloy across all torque levels. Shear Stress: Magnesium Alloy: Consistently displays lower shear stress compared to Cast Iron and Copper Alloy. Overall Assessment: While Cast Iron and Copper Alloy exhibit stable deformation responses, Magnesium Alloy stands out for consistently lower equivalent stress and shear stress values. The lower stresses in Magnesium Alloy, despite the observed total deformation variations, suggest a potentially higher resilience to stress under the specified torque conditions. Implications for Gear Assembly: Considering the findings, Magnesium Alloy emerges as a promising material for gear assembly in terms of minimizing stresses. However, the nuanced response of Magnesium Alloy to total deformations should be carefully considered in the context of specific application requirements. Cast Iron and Copper Alloy, with their stable deformation responses, may still be viable choices, particularly in scenarios where the emphasis is on predictable and consistent material behavior

References

[1] Congfang Hu, Gaode Geng, Pol D. Spanos, \"Stochastic dynamic load-sharing analysis of the closed differential planetary transmission gear system by the Monte Carlo method\", Mechanism and Machine Theory, Elesevier, 165 (2021). [2] Mehmet Sar?ta?, Özgür Gölbol, Pa?a Yayla, \"Finite element stress analysis of three-stage gearbox\", Ni?de Ömer Halisdemir University Journal of Engineering Sciences, 10(2), 784-790, 2021. [3] Prasad Matam, Dr. Nilesh Diwakar, Dr. A. Rajasekhar, \"Differential Gear Box To Reduce Vibration Using Different Materials For Vehicles-A Review\", Turkish Journal of Computer and Mathematics Education Vol.12 No.2, 2021. [4] Prathamesh Patil, Abhishek Pathak, Omkar Nikam, \"Design And Analysis Of Differential Of LMV Using Composite Materials\", JETIR, Volume 8, Issue 4, April 2021. [5] Sumeet Shinde, Piyush Pawar, Rushikesh Nalawade, \"Review Paper On Design Of Types Of Mechanical Differentials Used In Automobiles\", International Research Journal of Modernization in Engineering Technology and Science, Volume:03, Issue:01, January-2021. [6] Ravi, Nausad Khan, Rone, \"A Review Paper on Helical Gear on FEM and AGMA Standard for Computation and Comparative Study of Stress Induced on Gears\" International Journal of Engineering Research in Mechanical and Civil Engineering, Vol 4, Issue 9, September 2019. [7] Shubham Palve, Purushottam Kumar Sahu, \"Review Paper on Analytical and Finite Element Analysis of Spur Gears\", International Research Journal of Engineering and Technology, Volume: 06, Issue: 06, June 2019 [8] Xiaohan Tang, \"Structural Strength Analysis of Gearbox Casing Based on ABAQUS\", Materials Science and Engineering, 677, 2019. [9] Tangeti Naga Sai Sravan, Kondapalli Siva Prasad, \"Design and Analysis of Centrally Suspended Cage-less Limited Slip Differential\", Journal of Mechanical Engineering and Technology, Vol. 11 No. 2 June – December 2019. [10] Yogesh V. Patil, S. V. Karanjkar, Harshal A, Chavan, \"Review Paper on Design and Analysis of Gearbox Casing\", International Journal of Innovations in Engineering and Science, Vol 4, No.10 ,2019 [11] Kishor Toke, Girish C Kurkure, Shubham S Waghumbare, \"A Review on Design and Development of Modified Differential Gearbox\", International Research Journal of Engineering and Technology (IRJET), Volume: 05 Issue: 12, Dec 2018. [12] R. Karthick, V. Mohankumar, S. Mohanprabhu, \"Design and Analysis Of Differential Gear Box\", IJCRT, Volume 6, Issue 1, February 2018. [13] Sonali A. Mote, A. V. Gaur, Ajit. B. Gujale, \"FEM analysis of helical gear\", International Journal of Advance Research, Ideas and Innovations in Technology, 2018. [14] K. Dinesh Babu, M. Siva Nagendra, Ch. Phanideep, \"Design and Analysis Of Differential Gear Box In Automobiles\", International Journal of Mechanical Engineering and Technology, Volume 8, Issue 5, May 2017.

Copyright

Copyright © 2024 Nitin Parihar, Tripti Sharma. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.