Memory Optimization using Dynamic Programming: A Comprehensive

Abstract

Dynamic Programming (DP) is one of the main techniques applied in problem solving by breaking a complex problem into its small, easier parts. It focuses on how these parallel methods are applied in current parallel computing systems, especially shared memory systems using OpenMP and distributed memory systems using MPI. We analyzed and compared execution times, scalability, and communication costs in which these parallel DP methods perform well. Shared memory systems are easier to implement for small to medium problems because they have low communication costs. Distributed memory systems are better suited for large problems though distributed memory systems have higher communication costs. This gives one an idea of the strengths and weaknesses associated with different parallel DP methods. It also enables the choice of the most relevant methods according to the features of the computing problem.

Introduction

I. INTRODUCTION

Dynamic Programming (DP) is one of the more well-known decomposition approaches to complex optimization problems. It efficiently solves optimization challenges in many fields by ensuring that a subproblem is computed as often as possible, though it only does so once, storing the result for later use to avoid redundant computation. It is extremely efficient for problems with overlapping parts and good structures. A few classic problems solved by DP are the Knapsack problem and shortest-path algorithms, among others, which fall within combinatorial optimization challenges. However, with the problem size becoming big, other traditional DP methods may need even more memory and processing power. To solve this problem of high computing needs, techniques that use parallelization have been used to make DP algorithms work better. Shared memory systems allow all processors to use a common memory area. Here, processors can talk to each other directly by reading and writing to the same memory. OpenMP is mostly used here, offering an easy way to make DP algorithms run in parallel using commands for the compiler. OpenMP is effective for small and medium-sized problems since communication between processors takes much less time.

The operation of DP algorithms on two different system types shared memory systems using OpenMP and distributed memory systems using MPI is examined and contrasted in this survey article. differences regarding execution time, scalability, communication overhead, and how simple they are to implement will be exhibited. The paper presents various studies and results, intending to provide informative details about the advantages and disadvantages of choosing between shared and distributed memory systems for parallel DP algorithms.

II. LITERATURE REVIEW

The literature survey in the document focuses on the challenges and solutions related to memory-efficient dynamic programming [1] for pairwise local sequence alignment in computational biology [10]. Traditional methods struggle with storing all intermediate results in high-speed memory, necessitating checkpointing strategies to store selected computation stages and recompute missing values as needed. The document introduces an optimal checkpointing strategy, demonstrating its effectiveness compared to previous methods by Wheeler and Hughey (2000). The new approach optimizes the backtrace process, reducing the number of stages and run time required for computations, as evidenced by comparative data in Table 1. In bioinformatics, advancement is essential for increasing the effectiveness of sequence alignment tasks [8].

The study presents a method for automatically parallelizing and optimizing static and dynamic memory on MPSoCs [2]. The main point is to ensure proper mapping of data within the data memory hierarchy and optimize the way data statically and dynamically allocated are accessed and stored. The support tools [6] for automatic parallelization, static memory management, and dynamic memory management are also included in this framework [15] to maximize MPSoC's computing capabilities while addressing the complexity of high data transfer and storage requirements found in contemporary embedded applications.

[7] For developing the work for automating the parallelization and memory optimization for MPSoCs, the framework is proposed for use in development tools.

Significant resources are included in this framework, including static memory control to improve performance and automatic parallelization of sequential code to run in parallel based on user preferences. It also strongly emphasizes efficient data management so that fixed and changing memory utilization can be optimized for the special requirements of embedded applications in the MPSoC architecture. a new approach to solving DCOPs is presented in this paper because the objective and constraint functions change over time[3].

Conventional EAs fail to capture such dynamic variations in real-time as they take the use of a rigid feasible region [9]. The authors here proposed an MBDE algorithm by taking a hybrid memory scheme. In a hybrid memory scheme, authors used both short-term and long-term memory so that this problem can be avoided. It would indicate the existence of short-term memory to note down failed solutions which improves diversity, it also indicates the existence of long-term memory to hold the best possible and impossible solutions for the coming changes. A method of how changes may be noticed is created, and the group adjusts quickly based on how good things work by noting results over time with trial vectors.

A new IATM is introduced for switching between meeting goals and following limits which enables efficient control of the distribution when there are changes in the limits or objectives Tests on benchmarks with 1000 runs show that the MBDE compares very well with nine of the best methods according to the solution quality to the challenges introduced by dynamic optimization problems.

To solve the Knapsack Problem [11], this study compares the performance of distributed and shared memory dynamic programming methods [4], highlighting their effectiveness on various parallel systems. The two methodologies are compared in this work. OpenMP for shared memory and MPI for distributed memory through time of execution, scalability, and overhead management. The results are presented as shared memory being more appropriate for small to medium-sized problem sizes because of the decrease in overhead from communication, and distributed memory is shown to be better suited for large-scale problems. However, it incurs higher costs in terms of communication overhead. Moreover, the method discusses efficiency in the implementation associated with OpenMP [12] rather than the great scalability of MPI at what trade-off; thus, valuable insight is given for optimization in dynamic programming applications. Shared and Distributed Memory Models for Parallel Dynamic Programming Algorithms: A Comparison. In particular in the context of the Knapsack Problem that has not been included here for reasons of size.

Here, the code uses OpenMP for shared memory algorithms and MPI for distributed memory. Key measurements for performance are execution time, scalability, and communication overhead. The result shows that shared memory appears to work better for small to medium problems because it has less communication overhead. On the other hand, distributed memory only seems efficient for larger problems, but it comes with more communication costs. The experiment highlights a trade-off between the ease of use of OpenMP and the higher scalability offered by MPI, which is crucial for the experts in the field. [3]. It addresses the challenge of test case selection and prioritization during software testing, a challenge usually experienced where complete execution time exceeds what is available for execution which is the case most of the time in developing projects.

An algorithm for dynamic programming has been developed. It blends human judgment with objective techniques like computational optimization. This is accomplished by the provision of unambiguous, professional prioritizing with a recurrence formula that does not exceed gigabytes. For this reason, training in taxonomy should explain the various approaches. The algorithm is for the use of medium to large project sets and retains some memory space. The present dynamic programming algorithms are used to solve the shortest-path problem. Single-source shortest path (SSSP) and all-pairs shortest path (APSP) are the two scenarios that are discussed in this study. The author explains the main difficulties and how they solve them. The categorization informs readers of what's going on with dynamic programming [13]. It breaks down the problem into smaller subproblems, and the solutions to the subproblems can be combined in some optimal way to pick the best test cases.

The ultimate focus is on having the chosen test cases be meaningful within a period. Every test case is assigned a weight that gives a reflection of objective and subjective criteria. The objectivities include aspects such as time taken to execute, while the subjective refers to aspects that significantly influence one's choice of selecting test cases in one order more than another. The process followed by the algorithm defines the selection problem in terms of test case importance, execution time, and the available maximum time for the effective prioritization of test cases [14]. A Survey of Shortest-  Path Algorithms.

[5] The paper provides an extensive overview of the algorithms that focus on finding the shortest paths between vertices in a graph, a critical problem related to various applications ranging from network routing to traffic control, game development, etc. It categorizes these algorithms based on the system proposed, which explains the different options available in solving the shortest path problem.

It talks about both single-source shortest path (SSSP) and all-pairs shortest path (APSP) situations where the challenges and solutions fall into two different categories. In this categorization, the authors reveal the difficult challenges of finding the lowest-cost paths in a graph efficiently.

Table 1. Comparison Table

Table 1. Indicates that a significant trade-off exists between the two main approaches in parallel dynamic programming: resource-oriented and memory-oriented techniques. Resource-oriented techniques, emphasizing the best possible usage of resources, show better scalability and efficiency, especially when used with large-scale problems. As both key advantages are in the efficient use of more than one processing core, the gain comes with a reduction in overall execution time with the growth of problem size. It makes them appropriate for high-performance computing applications by enabling them to boost their processing power to handle huge and complicated datasets that simple speeds cannot handle. However, these can be heavy-duty resource-intensive, leading to more memory usage and bottlenecks in data synchronization and communication.

In comparison, memory-optimistic strategies will pursue reducing the footprint of computation memory often through techniques about efficient data structures or redundant calculations minimization. Scalability may be brought into question while moderate execution time gains may be attained, particularly for memory-constrained environments. For bigger problem sizes, gains from memory optimization are easily obfuscated by increasing energy consumption and an underutilization of parallel processing capabilities. Furthermore, memory-centric methods may potentially fail to scale performance across multiple processors while also suffering the unsalability of memory access as well as data sharing.

III. ANALYSIS AND DISCUSSION

The experiments in Table I illustrate the importance of these trade-offs between parallelization-focused and memory-optimized techniques for parallel DP. Techniques like these are designed to optimize performance in large-scale optimization problems but display very different emphases between either a focus on high-speed computation or resource conservation. Parallelization-Focused Techniques. Good scalability by strong parallelization-focused techniques demonstrates good leverage on both multi-core and distributed architectures. Such techniques that decompose the problem into subproblems and distribute the workload among several processors significantly reduce execution times for large problems. Since these techniques are computationally very efficient, especially for the systems with considerable resources of processing, they become a more than effective source of handling large data and intricate tasks. However, the cost is also paid in terms of increased memory usage and enhanced inter-processor communication overhead, specifically on distributed systems. Overhead causes frequent bottlenecks because it either involves synchronization or involves a memory bandwidth-constrained environment. Parallelization is the best strategy for achieving great scalability in big computational systems, despite these setbacks.

The comparative study of optimization trends for the MPI and OpenMP scheduling techniques between 2018 and 2024 is shown in Figure 1. The graph shows that over the observed years, for large problems trails behind for small problems in terms of optimization percentages.

The graph demonstrates how well the small problems approach performs when dealing with smaller problem sizes. The analysis highlights how important these optimization techniques are becoming in terms of increasing computational efficiency. Thus, the choice among the above methods is dependent on the size of the problem in question, the architecture of the system, and specific performance requirements. Parallelization-focused methods are more suitable for large-scale problems requiring a lot of computation. In smaller or energy-constrained environments, memory-optimized approaches have an acceptable balance despite their poor scalability.

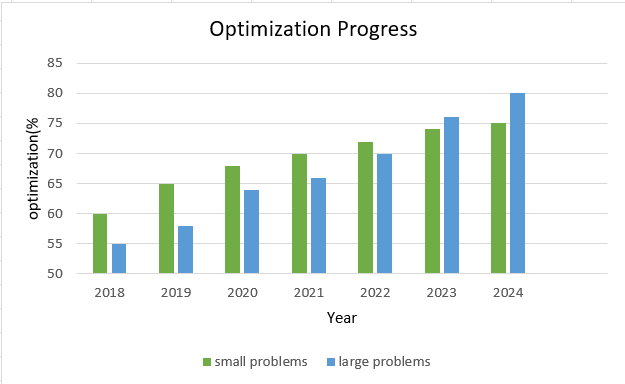
Figure 1. Performance Comparison of Optimization Progress

Figure 1 represents the trend of optimization concerning time for OpenMP (for small problems) and MPI (for large problems) titled "Optimization Trend: OpenMP vs MPI (2018–2024)". Initially, the optimization rate shown by OpenMP is higher, and it would cross around 70% only by 2020. This reflects the efficiency of shared memory systems for problem sizes without any high communication overheads. However, beyond 2020, the plateauing curve of OpenMP optimizations heralds the "performance ceiling" of scalability. On the other hand, the MPI presented optimization rates of around 55% in 2018 and increased steadily while overtaking OpenMP in 2023 and reached optimization rates up to around 80% in 2024. This may indicate that the use of MPI for distributed memory systems becomes more efficient when dealing with large-scale problems with improvements in the management of overhead in communication and scalability. The data emphasizes the severe trade-off: OpenMP shines for small-scale problems but quickly plateaus when dealing with large-scale workloads. MPI, at the same time, shows spectacular long-term scalability and optimization of large-scale complex problems and should therefore become a much-preferred approach to high-performance computing with an increase in problem size. This observation emphasizes the importance of choosing the proper parallel computing model as related to problem size and system architecture.

Conclusion

The suggested approach provides a versatile, effective, and scalable solution for handling big and complicated issues by combining the strength of dynamic programming with memory-constrained techniques. It saves a lot of memory by employing techniques such as a sliding window or recursive methods instead of building the whole DP table at the start; maintaining only necessary states or calculating intermediate results when needed. All choices encountered during the process are recorded and so, backtracking gives an exact solution. This ensures optimum performance under any variation of resource constraints and is thus perfectly suited to real-world applications wherein scalability and memory constraints are major bottlenecks. This algorithm provides a sophisticated yet useful framework through careful time and space trade-offs for many complex tasks. According to the authors of this study, shared and distributed memory models depend on both the size of a task and the available processing power to work best with parallel dynamic programming. OpenMP is said to be better suited for small to medium-sized problems compared to distributions that work based on shared memory due to simplicity and lesser overhead of communication. For large problems, however, MPI in distributed memory systems works better in scaling up at a cost of higher communication costs. The findings highlight a clear trade-off between ease of implementation and scalability, making shared memory models more practical for immediate applications and distributed memory models preferable for extensive, complex problems. Practitioners must carefully consider these factors when designing and optimizing dynamic programming solutions, especially for resource-constrained environments.

References

[1] Lee A. Newberg, Memory-efficient dynamic programming backtrace and pairwise local sequence alignment, Bioinformatics, Volume 24, Issue 16, August 2008, Pages 1772–1778, https://doi.org/10.1093/bioinformatics/btn308. [2] Y. Iosifidis, A. Mallik, S. Mamagkakis, E. De Greef, A. Bartzas, D. Soudris, F. Catthoor, \"A Framework for Automatic Parallelization, Static and Dynamic Memory Optimization in MPSoC Platforms,\" Journal of Embedded Systems, vol. 23, pp. 211-229, 2020. [3] C. Chenggang, T. Feng, Y. Ning, C. Junfeng, \"Memory-Based Differential Evolution Algorithms for Dynamic Constrained Optimization Problems,\" International Journal of Automation Engineering, vol. 30, pp. 193-206, 2021. [4] M. Posypkin, S. T. T. Sin, \"Comparative Performance Study of Shared and Distributed Memory Dynamic Programming Algorithms,\" Knapsack Problem Conference, vol. 18, pp. 123-135, 2022. [5] O. Banias, \"Dynamic Programming Optimization Algorithm Applied in Test Case Selection,\" Software Testing Journal, vol. 12, pp. 45-57, 2019. [6] A. Bartzas, et al., “Software metadata: Systematic characterization of the memory behavior of dynamic applications,” in Journal of Systems and Software, DOI: 10.1016/j.jss.2010.01.001. [7] C. Baloukaset al., “Optimization methodology of dynamic data structures based on genetic algorithms for multimedia embedded systems,” in Journal of Systems and Software, Volume 82, Issue 4, April 2009, Pages 590-602. [8] Wheeler,R. and Hughey,R. (2000) Optimizing reduced-space sequence analysis. Bioinformatics, 16, 1082–1090. [9] Nguyen, T.T., and Yao, X.: “Benchmarking and solving dynamic constrained problems”, in Editor (Ed.)^(Eds.): (IEEE, 2009, edn.), pp. 690-697. [10] Waterman,M.S. (1995) Introduction to Computational Biology. Maps, Sequences, and Genomes. Chapman & Hall / CRC, London, UK. [11] Hans Kellerer, Ulrich Pferschy and David Pisinger, “Knapsack Problems”, Springer, 2004. [12] Barbara Chapman, Gabriele Jost, Ruud van der Pas, “Using OpenMP: Portable Shared Memory Parallel Programming”, 2008, Volume 10. [13] T. J. McCabe, \"A complexity measure.\" IEEE Transactions on Software Engineering 4 (1976), pp.308-320. [14] Dan Hao, Lu Zhang, Lei Zang, Yanbo xWang, Xingxia Wu and Tao Xie, \"To Be Optimal Or Not in Test-Case Prioritization, IEEE Transactions on Software Engineering, Volume:PP, Issue 99, 2015, pp.1. [15] A. Madkour, W. G. Aref, F. U. Rehman, M. A. Rahman, S. Basalamah, \"A Survey of Shortest-Path Algorithms,\" Journal of Algorithms, vol. 34, pp. 27-42, 2020

Copyright

Copyright © 2024 Rutuja Borchate, Saloni Jibhe, Tanvi Bhandane, Prof. Dipti Pandit. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.