Abstract

The study focuses on the Convergent-Divergent nozzle for the different types of flow regions and Mach numbers such as subsonic region, sonic region and supersonic region. The Mach number of the nozzle changes across the nozzle, the Mach number varies from the subsonic region at the inlet and varies to the supersonic region at the exhaust of the nozzle. The fluid domain is made across the nozzle to capture the effects of the pressure and temperature and Multi physics analysis is also done to find the deformation depending on the material. The multi-physics analysis of the nozzle is done in COMSOL Multiphysics software by using the system coupling of the turbulent model, solid mechanics and heat transfer models. The results show the deformation of the nozzle under the action of chamber pressure and chamber temperature as the nozzle is the crucial part of any rocket or jet engine of an aircraft or rocket or launch vehicle. The Convergent-Divergent nozzle first converges the flow from the combustion chamber and then diverges the flow to get the maximum thrust at the convergent section the pressure of the fuel increases and then at the exhaust or convergent section suddenly increases enhances the thrust and velocity of the coming the exhaust fuel.

Introduction

I. INTRODUCTION

The nozzle is the crucial part of any aircraft or rocket that helps to control the exhaust thrust based on the geometry configurations and type of the rocket engine. The pressure inside the nozzle is referred to as Chamber pressure and is similar to the chamber temperature. The most commonly used nozzle is the De Laval nozzle commonly known as Convergent-Divergent nozzle (CD nozzle). This paper focuses on the De Laval nozzle, as the pressure and velocity inside the nozzle converge in the convergent section of the nozzle and combustion starts as the pressure and temperature start to increase and the pressure and temperature are maximum at the throat section of the nozzle and then the flow exhaust with the high velocity as it escapes through the throat of the nozzle. The study also focuses on the velocity of the exhaust gases as they undergo supersonic speed with a Mach number greater than 1 (M>1).

The study focuses on the effect of temperature and pressure on the nozzle to find the deformation of the nozzle at different frequencies. the functionally Graded Material (FGM) is used. The functionally graded material is the type of material that changes its properties in one or more directions according to the expression defined by the Sigmoid law or the power law. It is a class of composite material with varying properties according to the expressions.

The numerical scheme includes a partitioned fluid-structure interaction (FSI) algorithm in combination with a unified viscoelastic damage model. The paper focuses on the cooling channel wall which is made up of copper alloys. The liquid rocket engine is analysed under the action of the pressure force to find the sustainability of the copper alloys.(1) (2)A simple quasi-2-dimensional model to analyse the coupled problem of coolant flow and wall structure heat transfer in cooling channels of liquid rocket engine thrust chambers.(3) One-dimensional equations for coolant mass conservation and momentum balance. A two-dimensional equation for coolant energy balance coupled with the wall heat transfer balance in the radial direction.

The model utilizes semi-empirical relationships to estimate turbulent thermal conductivity and coolant-wall heat transfer coefficients. This approach enables rapid prediction of coolant flow evolution and temperature distribution throughout the cooling channel structure.(4)

The research focuses on the fuel leakage in piston couples using the mathematical models and fluid properties of the fuel, deformation and temperature. The leakage is most affected by the initial clearance between the piston and the sleeve. The leakage is more affected by the piston diameter, material stiffness and elasticity.(5)

The article describes a more realistic way to simulate the stresses on a solid rocket motor nozzle. Traditionally, these simulations ignore the friction between the parts of the nozzle(6). This new model includes a frictional coefficient to account for the rubbing between the parts.(7) The results showed that this inclusion mattered - it lowered the calculated stress on the nozzle. This is a more accurate way to simulate real-world behaviour, and it should be helpful for designing better rocket nozzles.(8)

Different types of vibrational analysis methods are used such as the Ritz method. Qian and Ching did the research on the cantilever beams with the Petrov-Galerkin (MLPG) method through the modal analysis of functionally graded material. To investigate the solution of simply supported FG beam using different sear deformation theories, Ayogdu and Taskin used the Navier type solution method.(9) The non-linear vibration response of the FGM beam is made using the direct numerical integration method and the Runge-Kutta Method(10). The exponential law and Euler-Bernoulli beam were used for the idealisation of several mechanical properties along the thickness direction.

Pandey and Parashar investigated the vibrational response of FGM beams with piezoelectric properties using the finite element method.(11) The frequency analysis of the FGM beam is also done with the piezoelectric properties using the Harmonic DQ method. Ebrahimi and Salari proposed the semi-analytical differential transform method that was used to examine the thermal effect on the modal behaviour of FGM nanobeams.(12) The modal analysis of the FGM plate in a hygrothermal environment was carried out using the Newton-Raphson Method. The effects of temperature and moisture changes, volume fraction index and length-to-thickness ratio on the eigenfrequency are also examined.(13) The eigenfrequency is identified based on the expressions given through the basic properties of the material like Young’s modulus, Poisson’s ratio etc.(14) The paper by Pankaj Sharma and Rahul Singh discussed the properties of FGM material, which is made of ceramic on the top surface and metal on the bottom surface.(15) The two different types of beam configurations are used to find the effects of the beam under the vibrations and hygrothermal effect.(16) The relentless pursuit of hypersonic flight necessitates the development of materials capable of withstanding a confluence of extreme conditions – scorching temperatures, substantial aerodynamic loads, and rapid pressure fluctuations(17). Functionally graded materials (FGM), with their meticulously tailored properties, offer a promising solution for these demanding applications. However, conventional analysis methods, which dissect these challenges into isolated domains like heat transfer or structural analysis, often fail to capture the intricate interplay between these phenomena. This is where Multiphysics analysis emerges as a cornerstone for the design and development of high-performance hypersonic vehicles.(18)

II. MATERIALS AND METHODS

Functionally graded materials are types of material which can change their properties according to the expressions and laws that are used to describe the properties of the materials. The few properties that are defined by functionally graded materials are Young’ modulus, poison ratio and density. These are used to define the basic properties required to do the different types of stress, pressure, vibrational, and thermal analysis of the material. The FGM material is an advanced form of composite.

The properties on which the Functionally graded material based is are given by, Functionally graded material used in this study is consists of two material, Zirconium Oxide and Hafnium Diboride composite. The properties of material are discussed below:

Table 1

A. Components of Materials

1) Zirconium Oxide:

a) Mechanical Properties:

• High Strength and Hardness: Zirconia is exceptionally strong and hard, even exceeding the strength of some steels. This makes it suitable for wear-resistant applications like grinding media, cutting tools, and ballistic armour.
• Fracture Toughness: Not only is it hard, but zirconia also exhibits good fracture toughness, meaning it can resist crack propagation. This enhances its durability under mechanical stress.
• Dimensional Stability: Zirconia has minimal thermal expansion and shrinkage, making it dimensionally stable over a wide temperature range. This is crucial for applications requiring precise tolerances.

b) Other Properties:

• High Melting Point: Zirconia boasts a very high melting point (around 2700°C), making it suitable for high-temperature applications like refractory materials or thermal barrier coatings.
• Electrical Insulator: In its pure form, zirconia acts as a good electrical insulator, useful in electronic components that require electrical isolation.
• Oxygen Ion Conductivity: At high temperatures, some forms of zirconia (e.g., stabilized zirconia) exhibit good oxygen ion conductivity. This property finds applications in solid oxide fuel cells and oxygen sensors.

2) Hafnium Diboride

1. High Melting Point: Hafnium diboride possesses an extremely high melting point, exceeding 3200°C (5800°F). This property makes it suitable for applications in extremely high-temperature environments.
2. Hardness: It is an extremely hard material, with a Vickers hardness value of around 30 GPa. This hardness makes it useful for applications requiring wear resistance.
3. Thermal Conductivity: Hafnium diboride exhibits high thermal conductivity, which makes it useful for applications where efficient heat dissipation is crucial, such as in electronic devices and high-temperature thermal management systems.
4. Electrical Conductivity: While not as high as metals, hafnium diboride still possesses significant electrical conductivity, which enables its use in applications requiring both thermal and electrical properties, such as in electrodes and certain electronic devices.
5. Chemical Stability: It has good chemical stability, particularly in non-oxidizing environments, which makes it resistant to corrosion and oxidation at high temperatures. However, it can react with certain chemicals under extreme conditions.

Table 2. Properties Comparison of Zirconium Oxide and Hafnium Diboride

B. Power Law and Sigmoid Law

A sigmoid function is a mathematical function that takes on an S-shaped curve. It's widely used in various fields because it exhibits a gradual increase or decrease over a specific range, approaching but never quite reaching fixed minimum and maximum values.

Xx1=X1-X20.5L2+x1L2n+X2

Were, X = mechanical parameters and numbers 1 and 2 define the materials 1 and 2 that are used, such as in the case Zirconium and hafnium are used.

n = Volume fraction index

A power law describes a relationship between two quantities where a change in one quantity results in a proportional change in the other, raised to a certain power. This proportionality holds regardless of the initial size of those quantities.

Xx1=X1-X20.5-x1Ln+X2

Were, X= Mechanical properties of the materials such as Young’s Modulus and Poisson's ratio of the materials combined to form a material.

C. Governing equations

Turbulent flow with the viscous model of k-?, the Inlet and outlet conditions are also taken. The governing equations involving the type of flow are given by,

Table 3. Description of fluid model

Functionally graded materials (FGM) are unique materials with properties that continuously vary throughout their structure. To analyse and predict their behaviour, a combination of mechanics, material properties, and heat transfer equations (when applicable) are employed. Here's a breakdown of the governing equations typically used:

1) Mechanics

1. Stress-Strain Relationship: This relates the applied stress (σ) to the resulting strain (ε) within the material. For FGMs, this relationship is often nonlinear due to the varying material properties. A common approach is to use a position-dependent Young's modulus (E(x)) in the constitutive equation:

σx=Ex*ε(x)

1. Equilibrium: This principle ensures that the material is in static equilibrium. It's achieved when the net force acting on a small element of the material is zero. This translates to the following equation:

dσxdx=0

1.  Material Properties Variation:

The key characteristic of FGMs is the continuous variation in properties. This variation is often described by a mathematical function. For example, the position-dependent Young's modulus (E(x)) can be expressed as a power law, exponential, or other functions depending on the specific FGM.

1. Heat Transfer:

If thermal analysis is important, heat transfer equations are incorporated. These can include:

1. Heat Conduction Equation: This equation describes how heat diffuses within the material. For FGMs, material properties like density (ρ(x)), specific heat capacity (cp(x)), and thermal conductivity (k(x)) become position-dependent:

ρx*cpx*dTdt=kx*d2Tdx2

III. GEOMETRY, MESHING AND BOUNDARY CONDITIONS

A. Geometry
The geometry of the convergent-divergent nozzle (CD Nozzle) is designed in Catia V5 software. The nozzle is classified under the perfectly expanded flow nozzle in which the ambient pressure is equal to the atmospheric or outside pressure. The geometry of the nozzle is given in the fig.

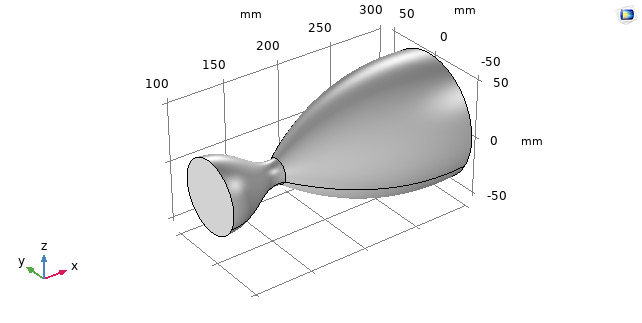
Fig. 1 Geometry of CD nozzle

B. Meshing

The meshing of the De Laval nozzle or CD nozzle is done in COMSOL Multiphysics software with the following parameters given, 
Table 4. Mesh quality and Size Index

Fig. 2. Mesh of the CD nozzle

C. Boundary Conditions

The boundary conditions are given for the nozzle at the inlet, outlet and the wall for the fluid flow and solid mechanics are given as the initial conditions and heat transfers as the initial temperature. The two types of coupling are also used in the analysis of the nozzle, Fluid-structure coupling and structural-thermal coupling.

Table 5. Inlet Conditions of the nozzle

D. Coupled Analysis

 In this research, two types of coupled or Multiphysics analysis are done to find the deformation and the mode shapes based on the eigen frequency of the nozzle under the effect of chamber pressure and chamber temperature. The first one is Fluid-Structure Interface, which is used to find the deformation in the nozzle under the effect of the chamber pressure and chamber temperature.

The second one is Heat Transfer-Solid mechanics Interface, which is used to find the heat transfer in the nozzle under the effect of chamber pressure in a perfectly expanded nozzle.

IV. RESULTS AND DISCUSSION

The pressure and velocity contours of the nozzle describes that at the inlet the pressure and velocity of the flow is increasing and the velocity and pressure is maximum at throat of the nozzle which signifies that the flow is incompressible and the compressed. At the exhaust section of the nozzle, the velocity suddenly increases as the cross-sectional area is increasing rapidly and the Mach number at the exhaust of the nozzle is greater than 1.

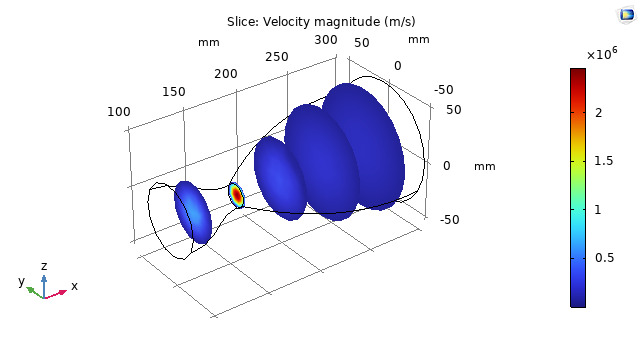
Fig. 3 Velocity contour

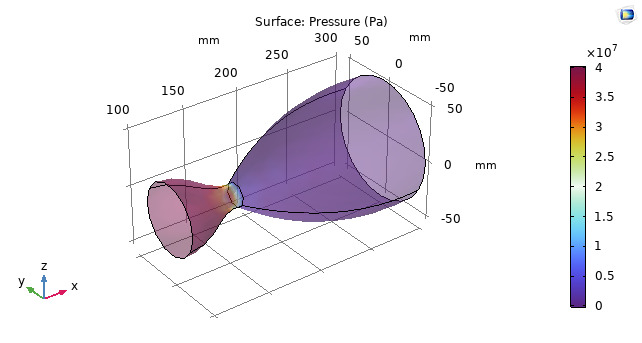
Fig. 4. Pressure Contour

The mode shapes of the nozzle according to the given frequencies and its displacements are given by,

Table 6. Eigen frequencies and displacement of the nozzle

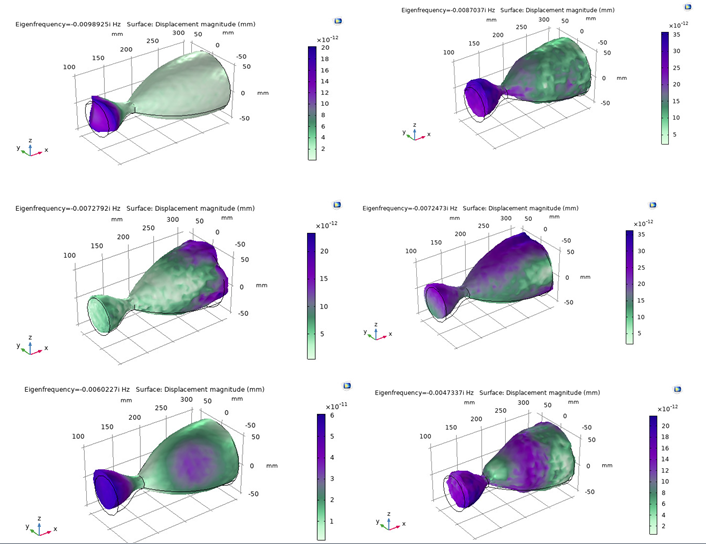
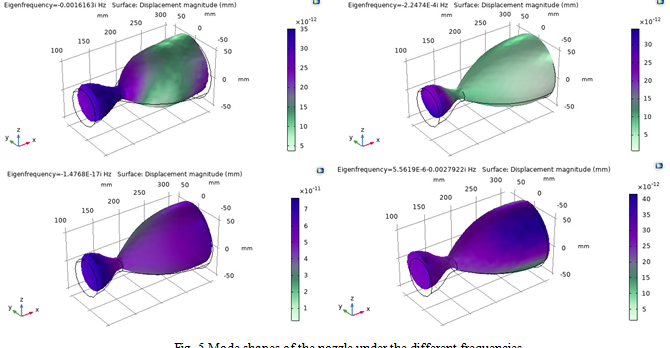
Fig. 5 Mode shapes of the nozzle under the different frequencies.

In the above mode shapes, the nozzle is tested at different frequencies to find that at which frequency the maximum deformation occurred. The violet colour describes about the maximum deformation the nozzle can undergo under the action of the pressure force and green colour describes that minimum deformation the nozzle can undergo under the effect of chamber pressure and chamber temperature.

Conclusion

This study investigated the convergent-divergent (CD) nozzle using coupled analysis in COMSOL Multiphysics software. The analysis focused on two main aspects: fluid flow and structural mechanics and heat transfer in solids. Functionally graded material (FGM) with properties varying along its length was used to analyse the nozzle\'s deformation under pressure and temperature loads. The results showed that: 1) Pressure and velocity increase rapidly in the convergent section, reached a maximum at the throat. 2) The flow accelerates in the divergent section due to the increasing flow area, reaching Mach 1 at the nozzle exhaust. 3) The coupled analysis predicted the deformation of the nozzle under realistic operating conditions. 4) The study also identified the eigenfrequencies of the nozzle, which can be crucial for avoiding resonance. This research provides valuable insights into the behaviour of CD nozzles under pressure and temperature loads. The use of FGM and couped analysis with all the three models offers a more realistic prediction of nozzle performance and can be helpful in designing high-performance and durable rocket engines.

References

[1] Liu Q. Coupling Heat Transfer and Fluid Flow Solvers for Multi-Coupling Heat Transfer and Fluid Flow Solvers for Multi-Disciplinary Simulations Disciplinary Simulations [Internet]. 2003. Available from: https://scholarsjunction.msstate.edu/td [2] Kowollik D, Tini V, Reese S, Haupt M. 3D fluid-structure interaction analysis of a typical liquid rocket engine cycle based on a novel viscoplastic damage model. Int J Numer Methods Eng. 2013 Jun 29;94(13):1165–90. [3] Yao SB, Luo Z, Wei K, Sun YH, Xu CY. Analysis of fluid-solid-thermal coupling characteristics of axial-symmetric vectoring exhaust nozzle. Proc Inst Mech Eng C J Mech Eng Sci. 2022 Sep 1;236(17):9472–84. [4] Pizzarelli M, Carapellese S, Nasuti F. A quasi-2-D model for the prediction of the wall temperature of rocket engine cooling channels. Numeri Heat Transf A Appl. 2011 Jan;60(1):1–24. [5] Yue P, Zhao J, Wei K, Ma X. The fluid–structure–thermal coupled characteristics of the leakage rate of piston couples interface for common-rail injector. Vol. 233, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. SAGE Publications Ltd; 2019. p. 5826–35. [6] Sun L, Bao FT, Shi W, Xu H. Coupled fluid, thermal and structural analysis of nozzle in solid rocket motor. In: Applied Mechanics and Materials. 2014. p. 297–301. [7] Zhu ZH, Cao M Sen, Xin ZQ, Li T. Analysis of fluid and solid interaction of the flexible bionic wing in ground effect. Proc Inst Mech Eng C J Mech Eng Sci. 2021 Jan 1;235(2):280–95. [8] Edathol J, Brezgin D, Aronson K, Dong Kim H. Prediction of non-equilibrium homogeneous condensation in supersonic nozzle flows using Eulerian-Eulerian models. Int J Heat Mass Transf. 2020 May 1;152. [9] Sharma P, Singh R, Hussain M. On modal analysis of axially functionally graded material beam under hygrothermal effect. Proc Inst Mech Eng C J Mech Eng Sci. 2020 Mar 1;234(5):1085–101. [10] Vashista M, Manik G, Verma OP, Bhardwaj B, editors. Recent Innovations in Mechanical Engineering [Internet]. Singapore: Springer Singapore; 2022. (Lecture Notes in Mechanical Engineering). Available from: https://link.springer.com/10.1007/978-981-16-9236-9 [11] Katili I, Syahril T, Katili AM. Static and free vibration analysis of FGM beam based on unified and integrated of Timoshenko’s theory. Compos Struct. 2020 Jun 15;242. [12] Sharma P, Singh R. Investigation on modal behaviour of FGM annular plate under hygrothermal effect. In: IOP Conference Series: Materials Science and Engineering. Institute of Physics Publishing; 2019. [13] Mechab I, Mechab B, Benaissa S, Serier B, Bouiadjra BB. Free vibration analysis of FGM nanoplate with porosities resting on Winkler Pasternak elastic foundations based on two-variable refined plate theories. Journal of the Brazilian Society of Mechanical Sciences and Engineering. 2016 Dec 1;38(8):2193–211. [14] Birman V, Byrd LW. Modeling and analysis of functionally graded materials and structures. Vol. 60, Applied Mechanics Reviews. 2007. p. 195–216. [15] Burlayenko VN, Sadowski T, Altenbach H. Efficient free vibration analysis of FGM sandwich flat panels with conventional shell elements. Mechanics of Advanced Materials and Structures. 2022;29(25):3709–26. [16] Singh R, Sharma P. A review on modal characteristics of FGM structures. In: AIP Conference Proceedings. American Institute of Physics Inc.; 2019. [17] Sharma P, Singh R. A numerical study on free vibration analysis of axial FGM beam. In: Materials Today: Proceedings. Elsevier Ltd; 2021. p. 1664–8. [18] Singh R, Sharma P. Free vibration analysis of axially functionally graded tapered beam using harmonic differential quadrature method. In: Materials Today: Proceedings. Elsevier Ltd; 2021. p. 2223–7.

Copyright

Copyright © 2024 Sahil Mathur, Rahul Singh . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.