Design and Analysis of a New Image Encryption Algorithm using Hyperchaotic System and Tent Map

Abstract

Users transfer millions of images every day in the era of information technology. Serious issues could arise if the information included in these photographs is open to unauthorised usage. There are numerous methods for protecting images. One of the most successful and well-known methods is digital image encryption. Confusion and diffusion are the two main phases of an encryption algorithm. This paper proposes a new image encryption technique that uses a hyperchaotic system and a tent chaotic map. With the help of random numbers produced by the 6D hyperchaotic system, the original image gets confused. A tent chaotic map is then used to create a key to diffuse the permuted image. Security analysis and time complexity are used to evaluate the suggested image encryption method\'s effectiveness. The security is tested using entropy, correlation coefficient, differential attacks, histograms, keyspace, sensitivity, noise, and data cut attacks. Additionally, the outcomes are compared using various encryption methods. The proposed method achieves a high level of security.

Introduction

1. INTRODUCTION

The regular process of digital image transmission over various networks involves the transfer of thousands of images every second. In healthcare networks, medical images are sensitive because wrong usage of them could lead to inaccurate diagnoses and subpar medical judgement. To prevent unauthorised access, high security standards are required while transferring military images via numerous networks. Social network users do not want their photographs to be accessible to others. These elements have elevated the importance of securing the data contained in digital images. Through a number of security measures, image secrecy is secured, making it impossible for an unauthorised individual to view the content of an image.

Data hiding, image watermarking, and encryption are the three main categories of image security techniques [1–5]. Data-hiding methods are used to integrate a hidden message that cannot be seen into the cover image. Digital data is inserted into the image when image watermarking techniques are applied, making the watermarked and original copies of the image visible. The key employed in image encryption methods transforms the digital input image into a noisy image that cannot be predicted or understood. Users are unable to access the encrypted image without the key.

A number of techniques are used for digital image encryption, including those based on DNA, the quantum approach, the chaos theory, and compressive sensing. Two crucial processes are used in image encryption methods. Confusion over which pixel arrangements are altered is the first stage. The second step, diffusion, depends on altering the pixel values. Inherent characteristics of chaotic-based approaches include non-periodicity, random behaviour, and sensitivity to initial conditions and control parameters. These characteristics make it possible to encrypt images successfully using chaotic-based techniques.

According to Chai et al. [6], chaotic-based digital image encryption systems can be split into two categories. One-dimensional chaotic maps are an example of a low-dimensional system that fits within this category. The second category includes high-dimensional systems such as hyperchaotic systems. The low-dimensional chaotic maps are comprehensible and practical due to their straightforward structures. Despite these intrinsic characteristics, these maps have a limited keyspace and low security levels. For the confusing procedure, Chen and Hu [7] developed a logistic-sine map-based approach for medical picture encryption. Liu et al. [8] employ a linked hyperchaotic system for pathological picture encryption. Zheng and Liu have created a brand-new technique for encrypting grayscale photos [9]. First, a novel 2D chaotic map system (2D-LSMM), based on both logistic and sine maps is presented. Next, a DNA-based encryption system is used, in which 2D-LSMM chaotic sequences are used to derive the encoding and operation rules for DNA sequences.

There are some limitations on related works, which are as follows:

1. Low sensitivity to the initial conditions and low keyspace.
2. Some encryption techniques are unable to recover the plain image when the encrypted image is subjected to noise and data cuts.
3. Because the histogram of the encrypted image is not flat, some of encryption techniques are vulnerable to statistical attacks.
4. The chaotic map's condition is independent of the plain image, which causes limitations in its ability to resist against differential attacks.

To get beyond the limits of low-dimensional chaotic systems, hyperchaotic techniques are applied. In terms of randomness, unpredictability, nonlinearity, and initial conditions, the hyperchaotic approaches performed better than the low-dimension chaotic methods.

The following is a summary of this paper’s contributions:

a. The 6D hyperchaotic system and a chaotic map are integrated to ensure a high level of security.

b. The proposed algorithm offers strong resistance to brute force attacks because to its large keyspace.

c. The proposed algorithm for image encryption is extremely resistant to most attacks.­­

II. MATHEMATICAL UNDERSTANDINGS

A. Six-Dimensional Hyperchaotic System

According to mathematical analysis, chaotic functions are often nonlinear with dynamic behaviour. They consequently react in ways that are unpredictable. According to past studies, when compared to low-dimension chaotic functions, hyperchaotic functions exhibit far more complicated dynamical behaviour. A hyperchaotic system must have at least four dimensions. Low-dimension chaotic functions only have one positive Lyapunov exponent in contrast to hyperchaotic systems. Wang and Yu [10] define the 6D Hyperchaotic System as follows:

III. THE PROPOSED METHODOLOGY

The cutting-edge method employed a Tent Chaotic map and a six-dimensional hyperchaotic system to encrypt the input image. The use of the 6D hyperchaotic system improves encryption performance and security levels due to its complicated, highly dynamic behaviour and two positive Lyapunov exponents. Tent Chaotic map is swift and able to diffuse the permuted image.

A. Encryption

The encryption consists of two phases: confusion and diffusion. The layouts and values of the pixels are altered in accordance with each of these processes. The 6D hyperchaotic system is the foundation of the confusion step. First, a calculation is made to determine the system's initial condition, which is based on the plain image. We then select three sequences after the hyper chaotic system is iterated to create a new vector (x2, x4, and x6). This vector's sorted number order is used to confuse the plain image. After confusing the plain image, the diffusion method is used to obtain the encrypted image. Our method's diffusion is based on a key produced by a Tent Chaotic map.

where P(m) is the probability of appearance of m. For grayscale images, the maximum value of entropy is 8. The randomness of the image's pixels is higher when the entropy number is close to 8. As part of this experiment, we encrypt the grayscale test images using the proposed algorithm and calculate the entropy values of the encrypted images, which are shown in Table 1. We can see from the observations that every entropy number is close to 8, which indicates that the encrypted images are truly random. Using our algorithm and the other encryption algorithms described in Table 2, the second test image (i.e., Lena) is encrypted. As can be seen, when compared to the various methods in Table 2, our presented method has a greater entropy value. We draw the conclusion from this test that our proposed technique ensures producing encrypted images with great randomness.

TABLE I: Encrypted Images entropy

TABLE II: Entropy value of our algorithm and other algorithms

B. Correlation Coefficient

In the input images, the neighbouring pixels frequently show a strong association in the diagonal, horizontal, and vertical axes. This correlation must be reduced for an encryption scheme to be effective. The following formula calculates the correlation coefficient between any two neighbouring pixels, A and B:

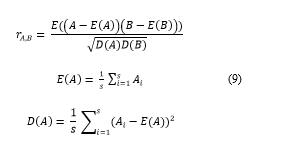
where the integer s referring to the total number of adjacent pixels; D(A) and E(A) stand for the variance and expectation of A, respectively.

In the horizontal (H), vertical (V), and diagonal (D) directions of the grey test images and their encrypted versions, Table 3 lists the correlation coefficient values for each. The correlation coefficient values of the test images are all close to one, whereas the correlation coefficient values of the encrypted images are close to zero. Table 4 provides a comparison of Lena image with other methods.

TABLE III: Correlation coefficient values

Table IV: Comparison of the Correlation Coefficient Values

Between our algorithm and other algorithms

C. Data Cut and Noise attacks

When images are exchanged over the network, noise or cropping (data cut) attacks are possible. Algorithms for image encryption should be resistant to noise and cropping attacks. The decrypted image quality is assessed using the widely used metric PSNR (peak signal to noise ratio). The PSNR for the original and decrypted images, IO, and ID according to mathematics is:

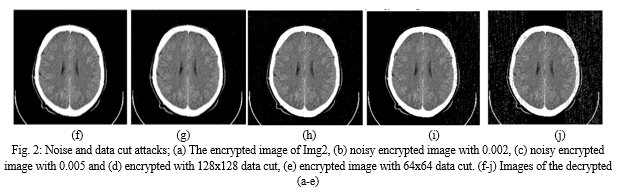
High image quality is indicated by a higher PSNR value. Original and decrypted images are indistinguishable for a PSNR > 35. The purpose of this experiment is to evaluate robustness against noise and data cut attacks. In this experiment, the new technique is used to decrypt an encrypted image that has been contaminated with "salt and peppers" noise at two distinct levels, 0.002 and 0.005. Additionally, a data cut of 64 x 64 and 128 x 128 is used to attack the encrypted images before the new approach is used to decrypt them. Table 5 displays the PSNR for the five test images with noise and data cuts.

The PSNR is reduced to 20dB when the encrypted image is attacked with a data cut off size of 128 x 128, which is a reasonably large cut off (i.e., the encrypted image lost 1/8 information). The decrypted image is recognizable despite the lower PSNR values. Fig. 2 illustrates the noise and data cut attacks for an encrypted image, showing how the reader can quickly identify the contents of the decrypted images in various scenarios. The new method is therefore robust and resistant to various attacks.

TABLE V: Peak signal to noise ratio (PSNR) (dB) values for

noise and data cut attacks

D. ??????????????Differential Attack

By figuring out the relationship between the original and encrypted images, the attacker hopes to decrypt the encrypted images without needing the key in this attack. Small modifications in the original image's pixels have a big impact on the encrypted version, making it more challenging for hackers to decrypt the encrypted version. This attack must be prevented by strong image encryption methods. Robustness to this attack is evaluated based on the Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) values obtained from following equations:

Symbols E1 and E2 refer to two encrypted images i.e., plain image and the modified image (made by changing one pixel in the plain image).  The image has a width of M pixels and a height of N.

Here, we compare the NPCR and UACI values between the two encrypted images in Table 6 to examine the effectiveness of our proposed methodology in defending against differential attacks. NPCR should be 99.6094%, and UACI should be 33.4635% with respect to their ideal values. Every value in Table 6 is near to their ideal values. A comparison of our approach and other image encryption algorithms can be seen in Table 7 for the original Lena image. The outcomes demonstrate how well our proposed method can withstand differential attacks.

TABLE VI: NPCR and UACI performances

TABLE VII: Comparison of NPCR and UACI

???????E. Histograms

The distribution of pixels in the image is shown by the histogram. The histogram for an encrypted image should be flat to make it impossible for attackers to predict any image data. Additionally, the histograms of the plain image and the encrypted image shouldn't be same. Using the new approach, three standard grayscale images Moon, Airplane, Clock were encrypted. The histograms of the encrypted images created using our method are uniform and distinct from those of the equivalent plain image histograms, as can be shown in Fig. 3. To ensure that the histogram of the encrypted image is uniform, a further experiment is conducted. The chi-square test (X2) used in this experiment is calculated by [19]:

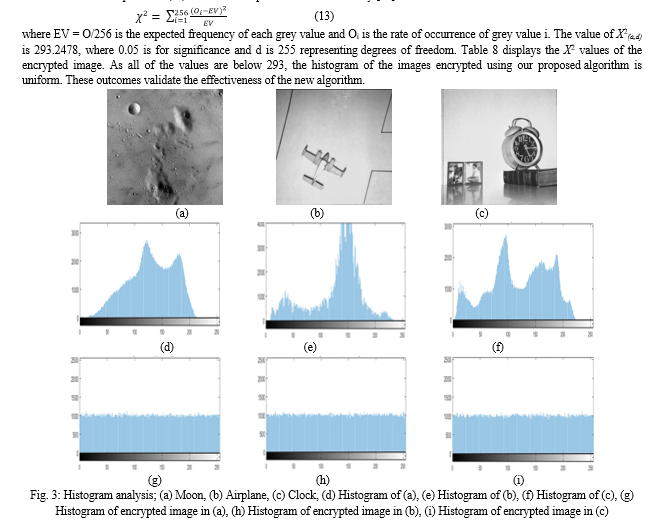
TABLE VIII: Chi-Square analysis

???????F. Keyspace

The size of the keyspace is important to the encryption process. If the keyspace size is greater than 2100, the encryption technique is resistant to brute force attacks. Different security keys are included in the proposed encryption algorithm: x1, x2, x3, x4, x5, x6, N0, a, b, c, d, e, and r. If we assume that the precision of the initial value is equal to 1016, then the total keyspace is greater than N0 x 1096, indicating robustness to a brute force attack.

???????G. Encryption Quality

1)  Maximum Deviation: By comparing the pixel values between the plain and encrypted images, the effectiveness of encryption is measured. If this difference is significant, the encryption algorithm is considered to be efficient. Calculating the maximum deviation includes:

???????

Conclusion

This paper introduced a new grey image encryption algorithm. The Tent Chaotic map is combined with a 6D hyperchaotic system in this algorithm. First, we choose three sequences from a 6D hyperchaotic system before changing the pixel positions. The Tent chaotic map is then used to change the pixel values of the shuffled image. The new technique is sensitive to small variations in the secret key and pixel distribution, producing a completely different encrypted image. As a result, the proposed algorithm successfully defends against the differential attack. When the keyspace size is large enough, the new algorithm can withstand a brute force attack. Additionally, information entropy, correlation coefficients, noise and data cut attack, and histogram are used to evaluate the security performance of the novel algorithm. The results demonstrate that the proposed algorithm performs well when encrypting grayscale images when compared to other recent encryption algorithms.

References

[1] Abdel-Aziz, M.M., Hosny, K.M. & Lashin, N.A. Improved data hiding method for securing color images. Multimed Tools Appl 80, 12641–12670 (2021), doi: 10.1007/s11042-020-10217-9. [2] K. M. Hosny, M. M. Darwish, K. Li and A. Salah, Parallel Multi-Core CPU and GPU for Fast and Robust Medical Image Watermarking, in IEEE Access, vol. 6, pp. 77212-77225, 2018, doi: 10.1109/ACCESS.2018.2879919. [3] Hosny, K.M., Darwish, M.M. Robust color image watermarking using invariant quaternion Legendre-Fourier moments. Multimed Tools Appl 77, 24727–24750 (2018), doi: 10.1007/s11042-018-5670-9. [4] Dolendro Singh Laiphrakpam, Manglem Singh Khumanthem, Medical image encryption based on improved ElGamal encryption technique, Optik, Volume 147, 2017, Pages 88-102, ISSN 0030-4026, doi: 10.1016/j.ijleo.2017.08.028. [5] Li, Y, Yu, H, Song, B, Chen, J. Image encryption based on a single-round dictionary and chaotic sequences in cloud computing. Concurrency Computat Pract Exper. 2021; 33:e5182, doi: 10.1002/cpe.5182. [6] Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process, 2019, 155, 44–62. [7] Chen, X.; Hu, C.-J. Adaptive medical image encryption algorithm based on multiple chaotic mapping. Saudi J. Biol. Sci. 2017, 24, 1821–1827. [8] Liu, H.; Kadir, A.; Liu, J. Color pathological image encryption algorithm using arithmetic over Galois field and coupled hyper chaotic system. Opt. Lasers Eng. 2019, 122, 123–133. [9] Zheng, J.; Liu, L. Novel image encryption by combining dynamic DNA sequence encryption and the improved 2D logistic sine map. IET Image Process. 2020, 14, 2310–2320. [10] Wang, J.; Yu, W.; Wang, J.; Zhao, Y.; Zhang, J.; Jiang, D. A new six-dimensional hyperchaotic system and its secure communication circuit implementation. Int. J. Circuit Theory Appl. 2019, 47, 702–717. [11] R Noha, HA HossamEldin, EE Said, and EA Fathi, (2015), Hybrid ciphering system of image based on fractional Fourier transform and two chaotic maps , International Journal of Computer Applications (0975 – 8887), 119 (11) 12–17. [12] Category: Computed Tomography Images of Mikael Häggström’s Brain, Sept. 2022, [online] Available: https://commons.wikimedia.org/wiki/Category:Computed_tomography_images_of_Mikael_H%C3%A4ggstr%C3%B6m%27s_brain. [13] File:Lenna (test image).png, Sept. 2022, [online] Available: https://en.wikipedia.org/wiki/File:Lenna_(test_image).png. [14] SIPI Image Database, Sept. 2022, [online] Available: https://sipi.usc.edu/database/database.php?volume=misc. [15] Tian, P.; Su, R. A Novel Virtual Optical Image Encryption Scheme Created by Combining Chaotic S-Box with Double Random Phase Encoding. Sensors 2022, 22, 5325. doi: 10.3390/s22145325. [16] S. T. Kamal, K. M. Hosny, T. M. Elgindy, M. M. Darwish and M. M. Fouda, \"A New Image Encryption Algorithm for Grey and Color Medical Images,\" in IEEE Access, vol. 9, pp. 37855-37865, 2021, doi: 10.1109/ACCESS. 2021. 3063237. [17] Q. Lu, C. Zhu and X. Deng, \"An Efficient Image Encryption Scheme Based on the LSS Chaotic Map and Single S-Box,\" in IEEE Access, vol. 8, pp. 25664-25678, 2020, doi: 10.1109/ACCESS.2020.2970806. [18] W. J. Jun and T. S. Fun, \"A New Image Encryption Algorithm Based on Single S-Box and Dynamic Encryption Step,\" in IEEE Access, vol. 9, pp. 120596-120612, 2021, doi: 10.1109/ACCESS.2021.3108789. [19] A. Banu S and R. Amirtharajan, ‘‘A robust medical image encryption in dual domain: Chaos-DNA-IWT combined approach,’’ Med. Biol. Eng. Comput., vol. 58, no. 7, pp. 1445–1458, Jul. 2020.

Copyright

Copyright © 2022 Girish Varma Vegesna, K. RamaDevi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.