Open Loop Predictive Control of Regular and Chaotic Dynamics of Switched Reluctance Motor

Abstract

The strong non-linearity of the magnetic circuit of switched reluctance machine (SRM) and the strong coupling between the parameters of the dynamic model lead to the unpredictable and chaotic behavior for certain values of its control frequency. This phenomenon which is due to the magnetic resonance of the rotor is characterized by a strong oscillation around an equilibrium position at each control pulse and conduct to chaotic dynamics behavior of SRM. In this work, we apply the technique of predictive control to the chaotic behavior of switched reluctance motor dynamics, in order to ensure a fast convergence of the rotor position towards stable equilibrium positions. The particle swarm optimization algorithm (PSO) is used to obtain an optimal value of the gain of the predictive controller used. Numerical simulations performed using the FEMM (for finite element calculation) and Matlab/Simulink software clearly show a good reduction of the rotor oscillations by applying the predictive control for a frequency taken in the periodic operating range of the machine and a total control of chaos for certain frequencies for which the machine exhibits chaotic behavior without controller. This work can be useful for machine engineers since the dynamic instability can be the cause of vibration and noise in the machine. The results obtained could then be useful and help avoid noisy operation of the machine for industrial applications.

Introduction

I. INTRODUCTION

The switched reluctance machine (SRM) has a good open-loop operation capability [1, 2].The ability to use an open loop SRM then allows performing a command without speed control. This has the effect of reducing the operation cost and increase the reliabylity. Indeed, the speed of the machine is related to the frequency of the phase voltage supplied. Thus, for an open loop high speed operation of the SRM, we can just increase the control frequency of the phase voltage. However, the interest of increasing the frequency in order to increase rotation speed can lead to the degradation of dynamic performances, questioning the synchronism principle of the machine. These results were obtained in part of our previous work on the description of the chaotic dynamical behavior of a SRM [3].

Although it has good open-loop operation capability, SRM is highly nonlinear and this makes its study very complex [4]. Compared to conventional machines, a major disadvantage of this machine is the strong torque ripple; phenomenon that contributes to acoustic noises and the mechanical vibration of its rotor [5]. In our previous study, we have shown that for some values of the control frequency, the rotor evolves completely unpredictably. This unpredictability has been likened to chaotic behavior of the machine [3]. However, it has been shown in the literature that torque ripples can be minimized by good optimization of the geometrical structure or by an adequate control technique of the machine [6, 7].

The optimization of the geometrical structure of the machine being very complex, it appears interesting to implement a control technique capable to extending the operation of the machine towards the high open loop control frequencies (whitout speed sensor). To the best of our knowledge, there is no related works on open loop predictive control of the switched reluctance motor with control of chaos. Indeed, many studies in the literature have focused on closed-loop control of switched reluctance motor without chaos control [8, 9, 10], hence the interest of this study.

The literature review is very rich in terms of chaos control techniques in classical chaotic dynamical systems. The first method of controlling chaos was proposed in 1990 and gave birth to the O.G.Y (Ott, Grebogi and Yorke) method [11]. This method applies to discrete-time chaotic systems or discretized chaotic systems. It consists of disturbing the system by periodically adjusting the control parameter so as to maintain the chaotic trajectory in a chosen periodic orbit. The OGY method is able to stabilize a chaotic dynamic on any unstable periodic orbit (UPO) contained in the chaotic attractor, as soon as its trajectory passes near the chosen UPO. The neighborhood must be chosen "small" so that the disturbance caused by the readjustment of the parameter does not modify the topology of the attractor.

This is the main weakness of this method, which, once locked down, can be very time consuming before the control becomes active. The second method is that of Pyragas (1992) or TDF (time delay feedback) which consists of applying adelayed continuous feedback to force the evolution of the system towards a desired dynamic, whenever the system passes in the vicinity of the desired dynamic behavior. This method applies to continuous time chaotic systems. Other chaos control techniques have been used in the literature to control chaos in classical chaotic dynamical systems. Among them, we can mention the predictive control [12, 1], the generalized backstepping method [10], the backstepping method [13] and several other methods [14, 15, 16].

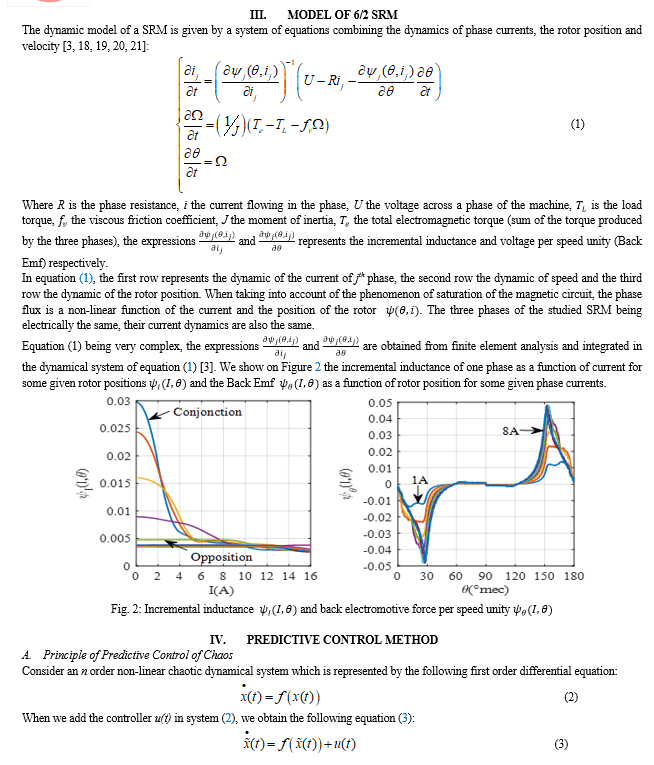
The dynamic model of a SRM is very complex because of its double nonlinearity (taking into account the phenomena of saturation of the magnetic circuit). It is thus important that the chosen model of chaos controller be the simplest and most effective possible. A heavy model would make the study even more complex. It is for this reason that the predictive control method has been chosen because of its efficiency and simplicity of implementation, both theoretical and experimental. However, for this method, the choice of the controller gain is not always optimized while the controller gain is an important parameter allowing the system to evolve into a stable periodic orbit [12].

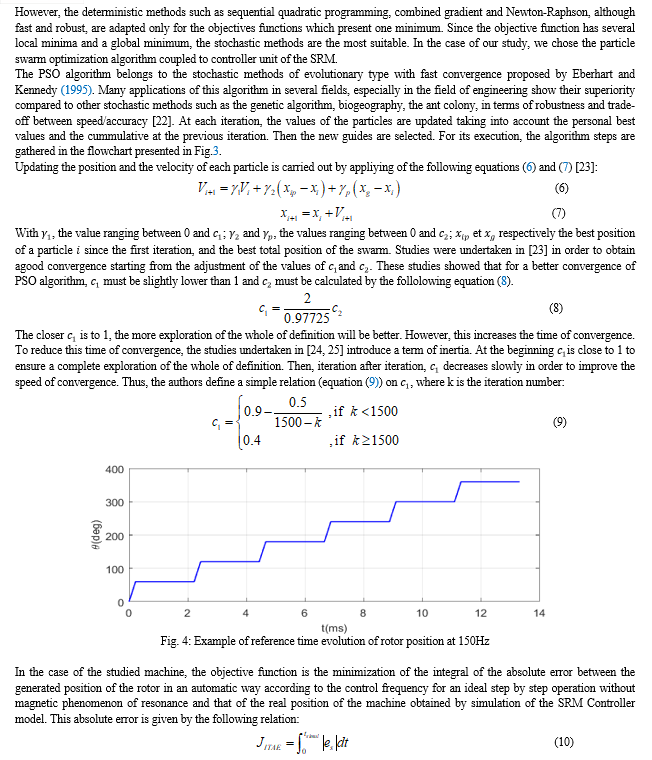
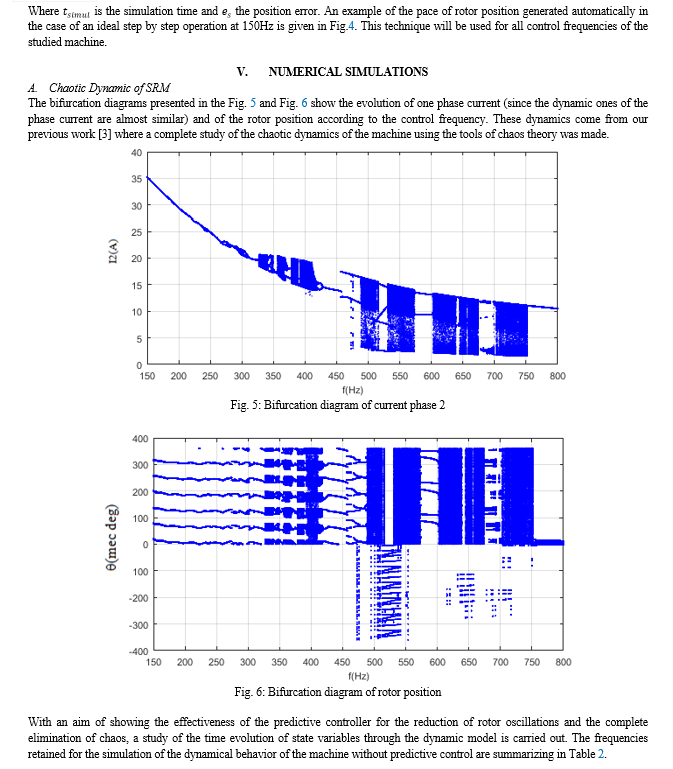
The present study therefore uses the predictive control method as a chaos control approach in a conventional open-loop 6/2 SRM considering the saturation phenomena of the magnetic circuit. The problem of obtaining optimal controller gain values for all frequencies is solved by using a particle swarm optimization algorithm coupled to the SRM-Controller set. The simulation results clearly show the reduction of rotor oscillations around the equilibrium positions when the machine is controlled at a periodic operating frequency, the reduction of the response time for selected frequencies in the chaotic behavior range of the machine and finally a complete elimination of chaos in the machine.

II. PRESENTATION OF THE SRM

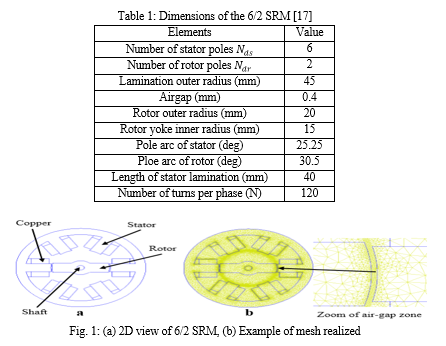
The study model is a double salience consisting of 6 stator teeth and 2 rotor teeth (DSSRM 6/2) whose geometric dimensions are given in Table 1. In order to facilitate the analysis of the electromagnetic parameters of this machine taking into account of the magnetic saturation phenomena, all the calculating steps have been programmed under the Matlab/Simulink software which will also control the FEMM finite element analysis field calculation software.

A cross-sectional view of this machine drawn with the FEMM software is given in Fig.1a with the identication of the different parts. Fig.1b shows an example of a mesh made on this machine where we make an enlargement at the air-gap to show the consistency of the mesh, since it is the electromagnetic exchange zone between the rotor and the stator.

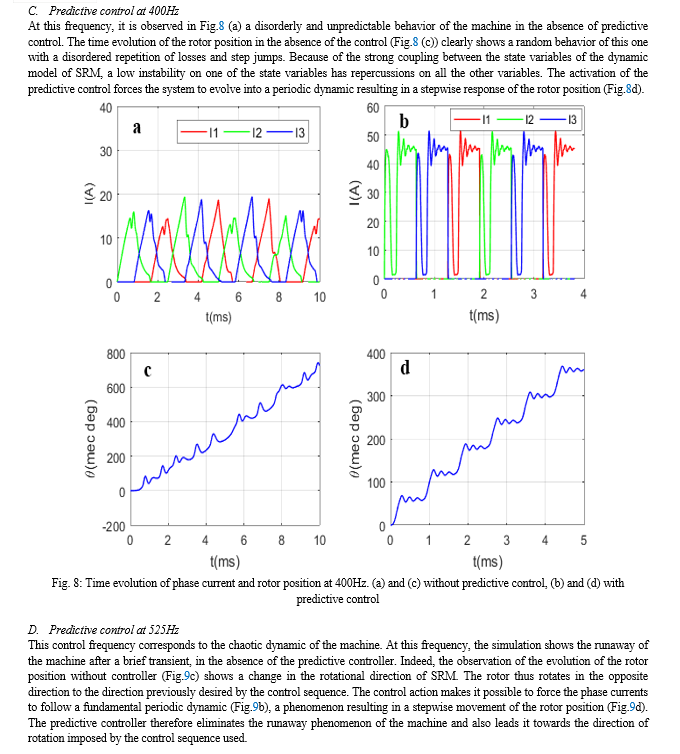
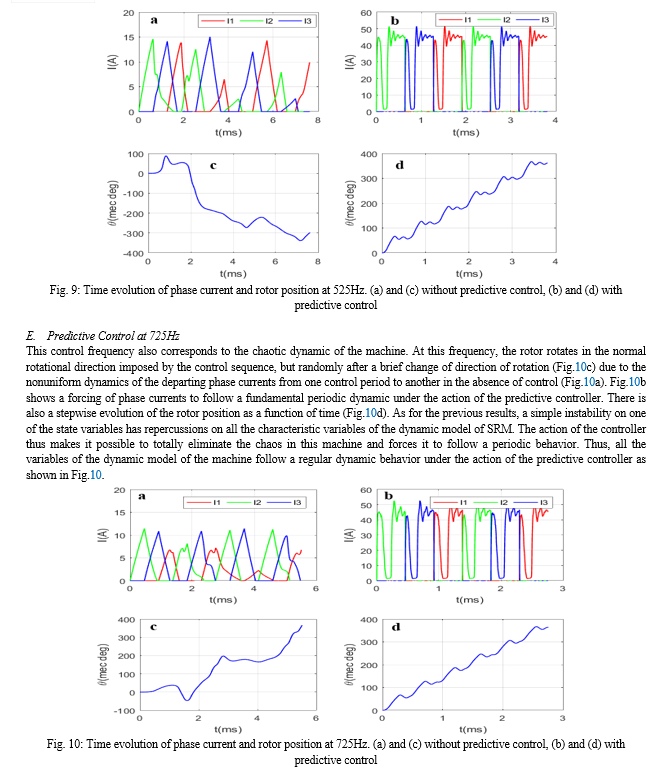
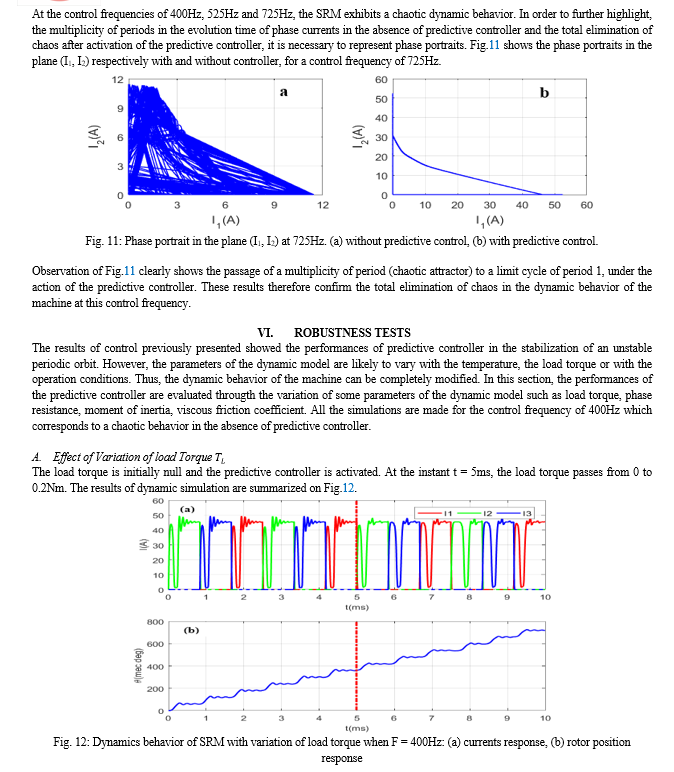
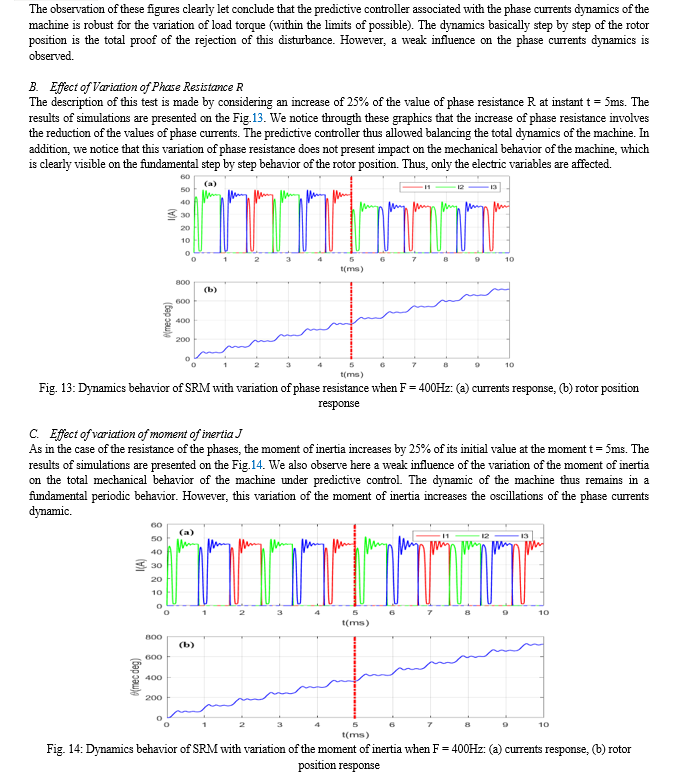
Conclusion

In this work, the predictive chaos control technique was used to reduce or eliminate the instabilities and multiplicity of periods appearing in the dynamic behavior of a 6/2 SRM, taking into account of the magnetic saturation phenomenon. The mathematical model of the 6/2 SRM was presented. A rich and varied dynamical behavior including chaos was obtained by plotting the bifurcation diagram of the system. Faced to the difficulty in calculating the gain of the predictive controller in the case of the doubly non-linear dynamic model, a stochastic method using the particle swarm optimization algorithm has been employed to derive optimal gains for some values of the control frequencies. Using these optimal gains, numerical simulations using the Matlab/Simulink software have shown a reduction in rotor oscillations around the equilibrium positions for a control frequency of 150Hz and elimination of chaos for the following control frequencies 400Hz, 525Hz and 725Hz. In addition, the analysis of the robustness has shown good performances of the controller with a total disturbance rejection which can occur spontaneously but also voluntary. In perspective, we plan to carry out a complete study of the machine under predictive control for the entire frequency range presented by the bifurcation diagram. Finally, an extension of the operation of the machine outside the frequency range used in this work will be done.

References

[1] Boukabou, A. Chebbah et N. Mansouri, « Predictive control of continuous chaotic systems,» International Journal of Bifurcation and Chaos, n° %118, pp. 587-592, 2008. [2] G. Zwe-Lee, K.-Y. K, H. Jia-Sheng, H. Min-Fu et T. MingHsiao, Design and Optimization of High-Speed Switched Reluctance Motor Using Soft Magnetic, https://doi.org/10.1109/IPEC.2014.6869593, 2014. [3] G. Guidkaya, J. Y. Effa et F. E. D. Kenmoe, «Chaotic dynamic behavior in switched reluctance motor taking into account magnetic saturation effects,» International Journal of System Assurance Engineering and Management, vol. 13, p. 1556–1571, 2022. [4] A. Tahour, Meroufel, H. Abid et A. Aissaoui, « Sliding Controller of Switched Reluctance Motor,» Leonardo Electronic Journal of Practices and Technologies, vol. 12, pp. 151-162, 2008. [5] V. Prabhu, V. Rajini et M. Balaji, « A Comparative Study of Operating Angle Optimization of Switched Reluctance Motor with Robust Speed Controller using PSO and GA,» J Electr Eng Technol, 2015. [6] B. Mirzaeian, M. Moallem, V. Tahani et C. Lucas, «Multiobjective optimization method based on a genetic algorithm for switched reluctance motor design,» IEEE Transactions on Magnetics, vol. 38, pp. 68-75, 2002. [7] Z. Xu, R. Zhong, L. Chen et S. Lu, « Analytical method to optimize turn-on angle and turn-on angle for switched reluctance motor drives,» Electric Power Applications, IET , vol. 6, pp. 593-603, 2012. [8] I. M. Namazi, A. Rashidi et M. Saghanian-Nejad, «Energy-based adaptative sliding mode speed controlfor switched reluctance motor drive system,» Iranian Journal of Electrical and Electronic Engineering, vol. 8, pp. 68-75, 2012. [9] L. Chouaib, S. Kamel, M. Belkacem, M. T. Benchouia et M. E. H. Benbouzid, «Speed control of 8/6 switched reluctance motor with torque ripple reduction taking into account magnetic saturation effects,» Energy Procedia, vol. 74, pp. 112-121, 2015. [10] R. Sahab et Z. Haddad, «Chaos control in nonlinear systems using the generalized backstepping method,» American Journal of Engineering and Applied Sciences, vol. 1, pp. 378-383, 2008. [11] E. Ott, C. Grebogi et A. Yorke, «Controlling chaos,» Physic. Rev. Lett, vol. 64, pp. 1196-1199, 1990. [12] T. Ushio et S. Yamamoto, «Prediction-based control of chaos,» Physics Letters A, 1999. [13] G. Chen et X. Dong, «On feedback control of chaotic continuous-time systems,» IEEE trans on CAS, 1993. [14] A. Boukabou et N. Mekircha, «Generalized chaos control and synchronization by nonlinear high-order approach,» Mathematics and Computer in Simulation, 2012. [15] J. Slotine, «Sliding controller design for nonlinear systems,» International Journal of Control. [16] X. Liu, « Impulsive stabilization and control of chaotic system,» Nonlinear Analysis, 2001. [17] I. Gourragui, «Modelisation numerique, optimization et commande de Machines à Reluctance Variable,» PhD thesis University of Metz, France, 2006. [18] M. R. Harris, A. Hughes et P. J. Lawrenson, «StaticTorque Production in Saturated Doubly-Salient Machines,» Proc. IEE, pp. 1121-1127, 1975. [19] R. S. Wallace et D. G. Taylor, «Three Phase Switched Reluctance Motor Design to Reduce Torque Ripple,» International Conference on Electrical Machines ICEM\'90, pp. 782-787, 1990. [20] J. Reinert, R. Inderka, M. Menne et D. R. W. De, «Optimisation Performance in Switched Reluctance Motor,» In APEC \'98 Thirteenth Annual Applied Power Electronics Conference and Exposition, 2000. [21] M. Sanada, S. Morimoto, Y. Takeda et N. Matsui, «Novel Rotor Pole Design of Switched Reluctance Motorsto Reduce the Acoustic Noise,» In Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy (Cat. No.00CH37129), 2000. [22] F. Nzanywayingoma et Y. Yang, «Analysis of Particle Swarm Optimization and Genetic Algorithm based on Task Scheduling in Cloud Computing Environment,» International Journal of Advanced Computer Science and Applications, vol. 8, pp. 19-25, 2017. [23] M. Clerc et P. Siarry, «Une nouvelle mta-heuristiquepour l\'optimisation difficile : la méthode des essaims particulaires,» J3EA 3, 007. DOI:10.1051/bib-j3ea:2004007, 2004. [24] Y. Shi et R. C. Eberhart, «Empirical study of particle swarm optimization, Evolutionnary Computation,» CEC 99, Proceedings of the 1999 Congress on 6-9 Jully 1999, vol. 3, pp. 1950-1953, 2003. [25] C. T. Ioan, « The particle Swarm Optimization algorithm: convergence analysis and parameters selection,» Information Processing Letters, pp. 317-325, 2003.

Copyright

Copyright © 2024 Guidkaya Golam, Effa Joseph Yves, Kenmoe Fankem Eric Duckler. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.