Effects of Operations of Various Water Reservoirs and Dams According to their Safety for the Surroundings Areas

Abstract

Dams are essential pieces of infrastructure that are required for river navigation, flood risk reduction, agriculture, water security, and the production of clean energy. However, controlling dam operations becomes more complex as a result of these several, frequently incompatible goals. Furthermore, dam infrastructure has been developing into intricate system-of-systems with several interdependent parts and subsystems that are all vulnerable to a variety of uncertainties. Due to these intricacies and uncertainties, numerous research projects centered on dam systems and reservoir operational safety have been initiated. This work focuses on the latter by doing research-on-research, or meta-research, on previously published studies in order to pinpoint important research gaps and suggest future lines of inquiry. In order to discover and categorize significant and latent issues in the discipline, this research first conducts a quantitative analysis of the relevant literature using text mining and then topic modeling. The highlighted subjects are then critically reviewed using qualitative analysis, which explores the concepts, definitions, modeling methods, and key research trends. The study specifically targeted seven topics: water supply management, flood risk, inflow forecasting, hydropower generation, climate change, optimization models, and risk-based assessment and management. The paper also identifies three primary research needs related to the lack of resilience-guided management of dam operational safety, modeling tool capabilities, and modeling idea constraints. In order to guarantee the resilience of such vital infrastructure, particularly in the era of climate change, this study provides an overview of the existing research on dam and reservoir operational safety, the knowledge gaps related to it, and possible future research avenues.

Introduction

I. INTRODUCTION

Dams are essential constructions that control the flow of water needed for irrigation and safeguard people from the effects of flooding. The world's need for energy and water, and consequently, securely operational dams, has been rising dramatically and quickly during the past century due to the extensive socioeconomic development. Furthermore, the significance of dams as climate risk mitigation infrastructure has lately come to light due to climate change. Dams can lessen the effects of climatological hazards including floods and droughts. Furthermore, a number of nations have become more dependent on dams to generate hydropower, which is seen to be the most effective clean energy source for lowering greenhouse gas emissions. As a result, the number of hydropower dams being built worldwide has surged dramatically over the last ten years to around 50,000, and this growth is anticipated to continue. Dams are extremely complex systems of systems with several intra-dependencies, comprising both physical (like gates and turbines) and non-physical (like maintenance time and human judgments) components, all of which contribute to their crucial importance. In the transportation, energy, food and agricultural, communications, and water sectors, dams are also interdependent with other dams in the same river system (also known as cascading dams) and with other vital infrastructure networks. Taking into account the multipurpose dam operational regulations, the intersectionality of dam operation objectives complicates decision-making. For instance, a high reservoir water level is necessary for effective hydropower generation, whereas a low reservoir water level is necessary for flood control activities.

Furthermore, dams are seen as essential for reducing the risk of climate change. However, because climate change adds uncertainties into meteorological and hydrological variables that directly affect the temporal and spatial availability of water for dam operations, it is expected to have an impact on the safety of dam operations. Dam and reservoir operations are severely hampered by these dynamic, complex, non-linear, and uncertain behaviours, which makes it difficult to comprehend and forecast operational failures of dam systems.

Extensive research has been undertaken to examine the safety of dam systems and reservoir operations under diverse stressors, given the devastating repercussions of such operational failures. To determine the crucial research gaps in the current field, a number of studies examined relevant, in-depth prior work. However, the selection of only a fraction of documents related to the particular sub-topic (such as optimization models) within the field was typically subjective in these traditional assessments. This is common in the literature, despite the fact that it shown how the interdependencies and multi-objectivity of dams make themes pertaining to dam systems and operational safety quite broad. Thus, using text analytics—a machine learning tool that extracts meaningful information from textual data—the current study first identifies and categorizes the primary research topics before revealing the latent topics and the major research gaps within the dam system. This is done by conducting research on published research, or meta-research.

In a variety of domains, including structural engineering, operational research, city resilience, and transportation, topic modeling is used to uncover latent topics. To be more precise, this study used two stages to symbolize the meta-research on reservoir operating safety and dam systems. Quantitative analysis is part of stage 1, where significant themes and latent subjects—those that don't occur frequently in the literature—are found through topic modeling. A qualitative review that looks at definitions, concepts, and current research trends pertaining to the identified themes is then included in Stage 2. This study can identify the main research gaps that are underrepresented in the literature and have a substantial influence on dam systems and reservoir operational safety by using both quantitative and qualitative evaluations.

II. METHODOLOGY

Analysis of Quantitative Data

A. Collection of data

In order to determine the main subjects in the field, this study used text analytics, or topic modeling, to examine over 100 journal papers that were pertinent to dam systems and operational safety. The first step in gathering data was looking up journal article titles on the Web of Science.

(https://www.webofknowledge.com,), the chosen articles were sifted by looking at their abstracts and assessing how pertinent they were to the field. Following this abstract-based screening procedure, the chosen papers underwent additional filtering, resulting in some journal articles that were taken into consideration for additional examination. Abstracts of the articles are taken into account during the analytical procedure. Various topic modeling studies typically use the abstract to represent the full article. Generally, abstracts use succinct, clear language to highlight the main findings from the study, research questions, methods, suggestions, and the general goal of the study.

B. Prior to Processing

The statistical analysis carried out within the topic modeling is adversely affected by the many sources of linguistic noise that are typically present in the raw abstracts of the chosen articles. Case type variations (like DAM and dam), special letters (like punctuation), word forms (like operation and operational), and the usage of English common words (like the, and, of) are the main causes of this linguistic noise. Therefore, in order to remove such linguistic noise, pre-processing is necessary prior to topic identification. Usually, pre-processing is carried out in four steps:

(1) All words are formatted in lower case using the transformation stage;

(2) the unstructured text is transformed into words for analysis using the tokenization step;

(3) The treatment phase is used to filter the text data by using a "stop" word list to exclude common words;

(4) the stemming step is used to eliminate all affixes and return them to the word stem.

C. Latent Dirichlet Allocation (LDA)

Blei et al. (2003) created the generative probabilistic model known as Latent Dirichlet Allocation (LDA), which is based on the probabilistic latent semantic analysis (pLSA) model. To determine the latent subjects in a collection of textual documents, the LDA model is employed in topic modeling (more information on how this model functions in scientific articles may be found). LDA's reasonable calculation time is its primary benefit over other topic models, such as related topic models. While preserving the crucial connections between the dimensions of the analyzed texts and their core subject, LDA drastically lowers the amount of dimensions inside the documents. As a result, the LDA model was used in a number of investigations in several domains, including structural engineering, music, and genetic data.

In the LDA model, each document (d), which is made up of a group of words (wd), is represented as a distribution of topics K (θd) (for example, in a two-topic model, document 1 is 70% of topic A and 30% of topic B). A distribution of words (ψk) characterizes each subject (k) (k ∈ K); for example, subject A has 10% of words 1, 20% of words 2, 30% of words 3, etc. By estimating the θd and ψk, the LDA model allows the user to use the frequently occurring terms associated with each subject to deduce the main topics covered in the examined documents. Two Dirichlet distributions, Beta (β) (i.e., per-topic-per-word probability) and Gamma (α), are used to evaluate the two distributions, ψk and θd.

(1) The analyzed documents are chosen by the model user (D);
(2) Determine the number of topics (K);

(3) According to:

a. The word distribution for each topic k (ψk), assessed by initial Dirichlet (β);

b. The topic distribution for each document d (θd), assessed by initial Dirichlet (α), the algorithm randomly allocates a specific topic kdi to each word wdi.

Where, wdi is the word (i) in the word collection (wd ) per document (d), d ∈ [1, D], i ∈ [1, Nd (number of words in wd )], and kdi is the topic assigned to the word i (wdi) in the document (d), kdi ∈ [1, K]; Water 2023, 15, x FOR PEER REVIEW 5 of 41

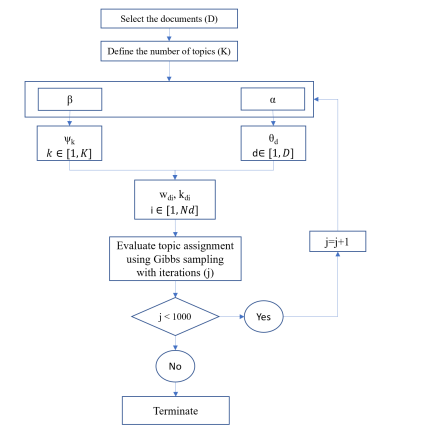
An illustration of the steps involved in the LDA algorithm.

(4) The algorithm enhances the topic assignment by increasing the values of β and α using Gibbs sampling with iteration j (in this study, j = 1000); it can then determine the likelihood that a word (wdi) is generated from the topic (kdi);

(5) The algorithm reassigns each word (wdi) with the new topic (kdi) based on the prior

Determining the ideal number of subjects (K) in the examined documents (D) is one of the trickiest parts of the LDA algorithm. Perplexity measurements were used in this study to identify the ideal amount of topics. In topic modeling, perplexity is a statistical metric that serves as a guide for choosing the ideal number of subjects. By determining the relative level of uncertainty across the probability models, perplexity metrics assess how well they can predict a sample; the optimal model should have the lowest perplexity value. The figure illustrates how the number of topics affects the perplexity evaluation values.

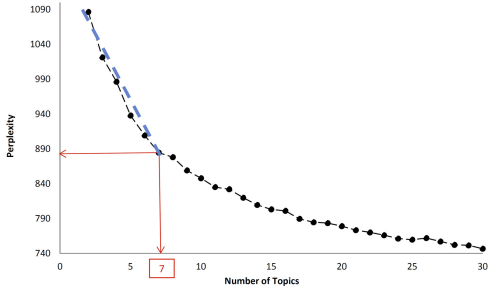
Perplexity plot (the link between perplexity and the number of issues).

D. Analysis of Qualitative Data

Though it is important to note that due to space constraints, this part is limited to succinctly presenting the definitions, concepts, modeling tools, and major research trends embraced in each of the highlighted themes, it does quote a significant number of the most current research articles. The study cites current review papers and textbooks that have been done to examine each issue in detail for further information regarding mathematical formulations and the application of modeling techniques. Additionally, it should be mentioned that the terms "reservoir" and "dam" are used interchangeably in this review in the literature to refer to the same dam and associated reservoir system.

E. Analysis of Qualitative Data

Using recent papers on dam and reservoir operational safety, this section attempts to provide a thorough analysis of the subjects mentioned in the previous section. Though it is important to note that due to space constraints, this section is limited to succinctly stating the definitions, concepts, modeling tools, and major research trends adopted in each of the seven topics that have been identified, it does cite a significant number of the most recent research papers. The study cites current review papers and textbooks that have been done to examine each issue in detail for further information regarding mathematical formulations and the application of modeling techniques. Additionally, it should be mentioned that the terms "reservoir" and "dam" are used interchangeably in this review and the literature, referring to the same dam and its reservoir system. Therefore, a more adaptable strategy is utilized, in which the best input-output solutions are first produced using optimization models, and the best operational rules are subsequently extracted using data mining techniques [38, 39]. In order to carry out these two methods in optimal dam operations challenges, a variety of sophisticated modeling tools are used. Figure 6 illustrates the five primary categories into which these sophisticated modeling tools, such as inference models, optimization programming techniques, and solution algorithms, can be divided: Multi-objective optimization (MLO) models, simulation-optimization (S-O) models, computational intelligence (CI) models, implicit stochastic optimization (ISO) models, and explicit stochastic optimization (ESO) models

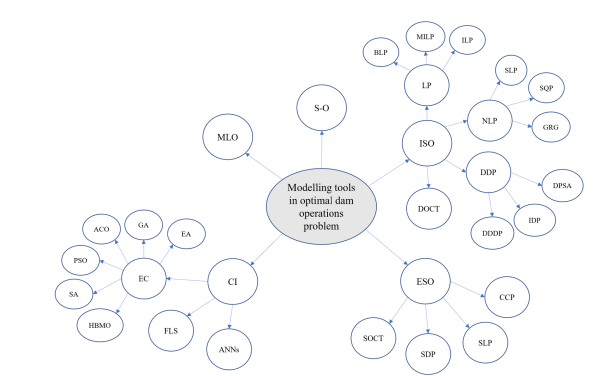
Categorization of the tools for optimization modeling in dam operations

Using deterministic optimization programming techniques like linear programming (LP) and its extensions (binary LP (BLP), integer LP (ILP), mixed-integer LP (MILP), non-linear programming (NLP) including successive LP (SLP), sequential quadratic programming (SQP), generalized reduced gradient (GRG), deterministic dynamic programming (DDP) and its modified models to solve its curse of dimensionality (dynamic programming successive approximation (DPSA), incremental DP (IDP), discrete differential DP (DDDP), and discrete-time optimal control theory (DOCT)), ISO is an optimization modeling technique that implicitly incorporates stochastic features of reservoir random variables. The best policies for a variety of historical or artificial time-series data for reservoir randomization can be produced by the deterministic optimization models. The operating rule curves from these produced best operating policies are then inferred using statistical inference techniques (e.g., multiple regression analysis), taking into account the reservoir conditions at the time (e.g., current storage level). Nevertheless, ISO modeling is a method that typically has a number of drawbacks. Such inferred operating rule curves, for instance, are specific to the input time-series data, whether it be synthetic or historical. Furthermore, the assumed operating rules may not be true if regression analysis yields low correlations. Additionally, inferring such operating principles using sophisticated inference techniques (ANNs, FRB) as opposed to regression analysis necessitates a significant computer investment because it takes numerous trials and errors to arrive at an effective conclusion.

In contrast to ISO, ESO modeling uses stochastic programming techniques like stochastic linear programming (SLP), stochastic dynamic programming (SDP), chance-constrained programming (CCP), and stochastic optimal control theory (SOCT) to explicitly provide the probabilistic description for the stochastic features of reservoir random variables. In this regard, the statistical frequency analysis can be used to fit the appropriate probability distribution (parametric or nonparametric) for the random reservoir variables. Therefore, it can be concluded that ESO has two benefits over ISO: (1) the optimization process takes into account the uncertainty of variables directly; and (2) the optimal operating rule may be found directly without the use of any interference tools. Nevertheless, ESO programming requires more computing power than ISO, especially when dealing with intricate multi-objective situations.

As an alternative, CI models resolve complicated issues that traditional approaches are unable to resolve. As a result, CI models are widely used in complex optimal dam operating problems, particularly as current computational capabilities are being developed.

The term "CI" describes a group of computational models inspired by nature, which typically comprise three primary techniques:

(1) fuzzy logic systems (FLS),

(2) artificial neural networks (ANN), and

(3) evolutionary computation (EC).

Metaheuristic algorithms like genetic algorithms (GA), ant colony optimization (ACO), particle swarm optimization (PSO), simulated annealing (SA), and honey bee mating optimization (HBMO) are included in EC models, also referred to as heuristic searching tools. Meta-heuristic algorithms are distinguished from other algorithms by their effectiveness in locating near-optimal (also known as Pareto optimal) solutions. In situations where traditional algorithms either fail to converge or become trapped in local optima, they can also calculate the best global solutions. As a result, EC-based algorithms can handle the complexity of reservoir operation problems such discontinuity, uncertainty, nonlinearity, multi-objectives, and discreteness by utilizing their special natural structure. See reviews for additional details on using metaheuristic algorithms to dam operation.

F. Management of Water Supplies

For many nations, water shortage is a rapidly growing issue that unavoidably impacts a range of social and economic sectors. Degradation of the environment causes water supplies to run out, which makes it impossible to provide the growing water needs brought on by socioeconomic growth. Furthermore, major drought occurrences are brought on by significant imbalances in water cycles caused by dry and hot weather waves brought on by global warming. Therefore, controlling the varying water flow and minimizing the disparities between water supply and demand depend on effective water supply management in dam operation. However, the ongoing depletion of water resources, multi-objective dam operations, the unpredictability of hydrological factors and water demand, and the potential for drought events add complexity to the rules governing water supply operation in order to ensure the best possible water allocation for multiple sectors.

Standard Operation Policy (SOP), Hedging Rules (HR), and other water supply regulations were used by dams to establish reservoir releases and the beginning and ending circumstances of water supply. SOP is one of these guidelines that is frequently applied in dam operations to meet water supply management standards. However, if there is enough water available, SOP completely relaxes water requests, reserving just the excess water for delivery in the future. As a result, SOP might not be effective in storing water discharge for dry seasons, which leads to acute water scarcity during droughts. In order to lessen the severity of drought situations, HR is therefore designed based on optimizing SOP operation guidelines. In normal circumstances, HRs accept lowering water supply discharge and set aside a portion of that discharge to lower the anticipated water shortage during droughts.

HRs are typically defined by two factors: the beginning and ending water availability. The water delivery operation adheres to HRs between these two places, and then follows SOP beyond them. Consequently, a number of HRs have been created, including the Reserve-storage two-point linear hedging rule, the Three-point linear hedging rule, the One-point linear hedging rule, and the Two-point linear hedging rule. Two primary questions are addressed by discrete phased hedging rules, which determine the HR parameters inside the beginning and finishing hedging points: (1) When to hedge? (2) How much should be hedged? See for additional details on contrasting these kinds of HRs in dam operations. The HR trigger and rationing factors parameters, respectively, are used to derive the answers to the two questions.

The rationing factor is the ratio of the lowered water supply from the original goal delivery (i.e., How much to hedge), whereas the trigger is the initial and terminate threshold at which the HR is to commence (i.e., "When to hedge?"). Typically, simulation models, optimization models, or simulation-optimization (S-O) models—which are outlined in subject 1 for further information—are used to determine these hedging rule parameters. See for additional information on quantifying HR parameters.

G. Forecasting Inflows

One of the most important factors in dam and reservoir operations is inflow. The risk of floods and droughts can be considerably decreased by using accurate inflow forecasts, which can also improve hydropower scheduling plans and water allocation methods for water supply management. As a result, a number of methods have been created to predict reservoir inflow. These methods fall into three categories: intellectual, physical, and statistical. To forecast inflow characteristics, physical and statistical techniques have been applied extensively in recent decades. Assuming that the behaviour of the historical data is applicable to the future (e.g., seasonal variation), statistical models are used to estimate the temporal inflow variation. These models include Autoregressive, Autoregressive Moving Average (ARMA), and Seasonal ARIMA for a comparison of the three models. Although the statistical methods are relatively simple and mature, they suffer from low accuracy in considering the dynamic, non-stationary, and non-linear inflow behaviour.

Alternatively, the physical models (e.g., soil and water assessment tools), including semi-and fully physically distributed models, use physical based equations (e.g., mass, momentum, or energy conservation equations) to represent the hydrological characterizations of the inflow data. Despite being very straightforward and advanced, statistical approaches have poor accuracy when it comes to taking into account dynamic, non-stationary, and non-linear influx behaviour. As an alternative, the hydrological characterizations of the inflow data are represented by physical-based equations (such as mass, momentum, or energy conservation equations) in the physical models (such as soil and water assessment tools), including semi-and completely physically distributed models. Despite being more accurate than conceptual hydrological models, physical-based models typically involve intricate mathematical processes, several parameter calibrations, and difficult initial/boundary condition determination. See for further information on contrasting the conceptual and physical hydrological models. As an alternative, sophisticated cognitive techniques including artificial neural networks, support vector machines, and decision-making algorithms were used to get around the drawbacks of the physical and hydrological forecasting models.

The capacity to give real-time forecasting and incorporate external factors (like weather) that can increase predicting accuracy is the primary benefit of such data-driven models.

Furthermore, data-driven models require far less input and parameter data because they solely rely on previous hydro-meteorological data, not on underlying physical processes. for contrasting the physical and data-driven models. However, data representation (i.e., data quality) can impact the learning and extraction features of the historical data, which in turn can impact the forecasting accuracy of the data-driven models. Furthermore, it might not be enough to use just one data-driven model because each one contains elements that might not be appropriate for the hydrological characteristics of all rivers. Consequently, hybrid models have lately been created to take into account the benefits of each forecasting model.

Conclusion

Dam operational management is severely hampered by the intricacy of dam systems-of-systems, the multi-objective nature of their operations, and their unpredictable susceptibility to climate change. Despite the importance of dam infrastructure to society, these difficulties led to a great deal of research into the operational safety of dams from a variety of angles. This work meta-researches (quantitatively and qualitatively) the complete published literature on dam and reservoir operating safety from 1984 to 2023, in contrast to prior studies that subjectively only took into account particular subjects and related documents. In order to uncover the latent subjects in dam and reservoir operational safety, this meta-research will first identify and categorize the important topics. The main research gaps are then found as chances for further study by qualitatively analyzing such dormant subjects. More precisely, 871 relevant journal articles are analyzed using textual topic modeling to identify seven major topics. These include risk-based assessment and management, inflow forecasts, hydropower generation, flood risk, climate change, optimization models, and water supply management. The contribution of these subjects to the relevant literature is then discussed, emphasizing that, in comparison to the other five issues, optimization models, flood risk, and risk-based assessment and management are given less attention in the literature. The significance of the quantitative analysis extends beyond just identifying the various subjects covered and outlining how each topic adds to the body of literature. Three main research gaps in dam safety assessment studies were found using quantitative and qualitative analyses. These gaps were related to the absence of development and adoption of resilience-guided management techniques, as well as limitations in modeling concepts and modeling tools. All things considered, this study offers a roadmap of the literature on operational safety for dams and reservoirs as well as related knowledge gaps.

References

[1] Ehsani, N.; Vörösmarty, C.J.; Fekete, B.M.; Stakhiv, E.Z. Reservoir operations under climate change: Storage capacity options to mitigate risk. J. Hydrol. 2017, 555, 435–446. [2] Regan, P.J. Dams as systems—A holistic approach to dam safety. In Proceedings of the U.S.S.D. Annual Meeting and Conference 2010, Sacramento, CA, USA, 12–16 April 2010; pp. 1307–1340. [3] Kumar, K.; Saini, R.P. A review of operation and maintenance of hydropower plants. Sustain. Energy Technol. Assess. 2022, 49, 101704. [4] Hauera, C.; Wagnera, B.; Aignera, J.; Holzapfela, P.; Flödla, P.; Liedermanna, M.; Trittharta, M.; Sindelara, C.; Pulgb, U.; Klöscha, M.; et al. State of the art, shortcomings and future challenges for a sustainable sediment management in hydropower: A review. Renew. Sustain. Energy 2018, 98, 40–55. [5] Neboh, N.; Adeyemo, J.; Enitan, A.; Olugbara, O. A review of applications of evolutionary algorithms to reservoir operation for hydropower production. Int. J. Geol. Environ. Eng. 2015, 9, 1153–1159. Available online: https://zenodo.org/record/1109762# .YvAJqHbMK38 [6] You, L.; Li, C.; Min, X.; Xiaolei, T. Review of dam-break research of earth-rock dam combined with dam safety management. Procedia Eng. 2012, 28, 382–388. [7] Rani, D.; Moreira, M.M. Simulation–Optimization modeling: A survey and potential application in reservoir systems operation. Water Resour. Manag. 2010, 24, 1107–1138. [8] Sun, L.; Yin, Y. Discovering themes and trends in transportation research using topic modeling. Transp. Res. Part C Emerg. Technol. 2017, 77, 49–66. [9] Gatti, C.; Brooks, J.; Nurre, S. A historical analysis of the field of OR/MS using topic models. arXiv 2015, arXiv:1510.05154. [10] Haggag, M.; Ezzeldin, M.; El-Dakhakhni, W.; Hassini, E. Resilient cities critical infrastructure interdependence: Meta-research. Sustain. Resilient Infrastruct. 2020, 7, 291–312. [11] Ezzeldin, M.; El-Dakhakhni, W. Meta-researching structural engineering: Trend identification and knowledge gap discovery using text mining. J. Struct. Eng. 2020, 146, 1–22. [12] Islam, A.; Hassini, S.; El-Dakhakhni, W. A systematic bibliometric review of optimization and resilience within low impact development stormwater management practices. J. Hydrol. 2021, 599, 126457. [13] Das, S.; Sun, X.; Dutta, A. Text mining and topic modeling of compendiums of papers from transportation research board annual meetings. J. Transp. Res. Board 2016, 2552, 48–56. [14] Griffiths, T.L.; Steyvers, M. Finding scientific topics. Proc. Natl. Acad. Sci. USA 2004, 101, Natural Language Processing: Trends and Applications; Springer: Cham, Switzerland, 2018; pp. 373–397. [15] Miner, G.; Elder, J.; Hill, T.; Delen, D.; Fast, A.; Nisbet, R.A. Practical Text Mining and Statistical Analysis for Non-Structured Text Data Applications; Academic Press: Cambridge, MA, USA, 2012. [16] Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. 30. Hofmann, T. Probabilistic latent semantic indexing. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (S.I.G.I.R. ‘99), A.C.M., Berkeley, CA, USA, 15–19 August 1999; pp. 50–57. [17] Amado, A.; Cortez, P.; Rita, P.; Moro, S. Research trends on big data in marketing: A text mining and topic modeling-based literature analysis. Eur. Res. Manag. Bus. Econ. 2018, 24, 1–7. [18] Steyvers, M.; Griffiths, T. Probabilistic topic models. In Latent Semantic Analysis: A Road to Meaning; Landauer, T., McNamara, D., Dennis, S., Kintsch, W., Eds.; Laurence Erlbaum: Hillsdale, NJ, USA, 2007; Volume 427, pp. 424–440. [19] Blei, D.M. Probabilistic topic models. Commun. ACM 2012, 55, 77–84. [20] Minka, T. Estimating a Dirichlet distribution. In Technical Rep.; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000. [21] Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [22] Fayaed, S.S.; El-Shafie, A.; Jaafar, O. Reservoir-system simulation and optimization techniques. Stoch. Environ. Res. Risk Assess. 2013, 27, 1751–1772. [23] Taghian, M.; Rosbjerg, D.; Haghighi, A.; Madsen, H. Optimization of conventional rule curves coupled with hedging rules for reservoir operation. J. Water Resour. Plan. Manag. 2014, 140, 693–698. [24] Parvez, I.; Shen, J.; Hassan, I.; Zhang, N. Generation of hydro energy by using a data mining algorithm for the cascaded hydropower plant. Energies 2021, 14, 298. [25] Bozorg-Haddad, O.; Aboutalebi, M.; Ashofteh, P.S. Real-time reservoir operation using data mining techniques. Environ. Monit. Assess. 2018, 190, 594. [26] Raju, K.; Chandre, G.C.; Karthika, B.S. Optimization of reservoir operation using linear programming. Int. J. Recent Technol. Eng. 2020, 8, 2277–3878. [27] Needham, J.T.; David, W.; Watkins, D.W.; Lund, J.R.; Nanda, S.K. Linear programming for flood control in the Iowa and Des Moines rivers. Water Resour. Plan. Manag. 2000, 126, 118–127. [28] Houck, M.H.; Cohon, J.L. Sequential explicitly stochastic linear programming models: A proposed method for design and management of multi-purpose reservoir system. Water Resour. Res. 1978, 14, 161–168. [29] Wu, X.; Wu, Y.; Cheng, X.; Chuntian Cheng Li, Z.; Wu, Y. A mixed-integer linear programming model for hydro unit commitment considering operation constraint priorities. Renew. Energy 2023, 204, 507–520. [30] Dogan, M.S.; Lund, J.R.; Josue Medellin-Azuara, J.M. Hybrid linear and nonlinear programming model for hydropower reservoir optimization. J. Water Resource. Plan. Manag. 2021, 147, 06021001. [31] Arunkumar, R.; Jothiprakash, V. Optimal reservoir operation for hydropower generation using a non-linear programming model. J. Inst. Eng. Ser. A 2012, 93, 111–120. [32] Gu, J.J.; Guo, P.; Huang, G.H.; Shen, N. Optimization of the industrial structure facing sustainable development in resource-based cities subjected to water resources under uncertainty. Stoch. Environ. Res. Risk Assess. 2012, 27, 659–673. [33] Simonovic, S.P.; Marino, M.A. Reliability programming in reservoir management, single multipurpose reservoir. Water Resour. Res. 1980, 16, 844–848. [34] Nandalal, K.D.W.; Bogardi, J.J. Dynamic Programming-Based Operation of Reservoirs: Applicability and Limits; Cambridge University Press: Cambridge, UK, 2007. [35] Labadie, J.W. Optimal operation of multi-reservoir systems: A state-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [36] Shim, K.-C.; Fontane, D.; Labadie, J. Spatial decision support system for integrated river basin flood control. J. Water Resour. Plan. Manag. 2002, 128, 190–201. [37] Yakowitz, S. Dynamic programming applications in water resources. Water Resour. Res. 1982, 18, 673–696. [38] Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; ISBN 0-691-07951-X. 55. Mizyed, N.; Loftis, J.; Fontane, D. Operation of large multi-reservoir systems using optimal-control theory. J. Water Resour. Plan. Manag. 1992, 118, 371–387. [39] Pontryagin, L.; Boltyanskii, V.; Gamdrelidze, R.; Mishchenko, E. The Mathematical Theory of Optimal Processes; Interscience: New York, NY, USA, 1962. [40] Lee, Y.; Kim, S.K.K.; Ko, I.H. Two-stage stochastic linear programming model for coordinated multi-reservoir operation. In Proceedings of the Operations Management 2006: Operating Reservoirs in Changing Conditions, Sacramento, CA, USA, 14–16 August 2006; Zimbelman, D., Loehlein, W.C., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 400–410, ISBN 978-0-7844-0875-9. [41] Seifi, A.; Hipel, K. Interior-point method for reservoir operation with stochastic inflows. J. Water Resour. Plan. Manag. 2001, 127, 48–57. [42] Juárez ML, A.; Ramírez, R.M.; Mora, R.D.; Reséndiz, A.M.; Esteban, R.V.; De la Cruz Courtois, O.A.; Elizondo, E.C. Guide curves in stochastic dynamic programming to optimize operation policies in sequential hydropower dams. Stoch. Environ. Res. Risk Assess. 2023. [43] Fayaed, S.S.; Fiyadh, S.S.; Khai, W.J.; Ahmed, A.N.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Koting, S.; Mohd, N.S.; Jaafar, W.Z.B.; et al. Improving dam and reservoir operation rules using stochastic dynamic programming and artificial neural network integration model. Sustainability 2019, 11, 5367. [44] Liu, P.; Zhao, J.; Li, L.; Shen, Y. Optimal reservoir operation using stochastic dynamic programming. J. Water Resour. Prot. 2012, 4, 342–345. [45] Tilmant, A.; Faouzi, E.H.; Vanclooster, M. Optimal operation of multi-purpose reservoirs using flexible stochastic dynamic programming. Appl. Soft Comput. 2002, 2, 61–74. [46] Azaiez, M.N.; Hariga, M.; Al-Harkan, I. A chance-constrained multi-period model for a special multi-reservoir system. Comput. Oper. Res. 2005, 32, 1337–1351. [47] Ouarda, T.; Labadie, J. Chance-constrained optimal control for multi-reservoir system optimization and risk analysis. Stoch. Environ. Res. Risk Assess. 2001, 15, 185–204. [48] Kitanidis, P.K. A first-order approximation to stochastic optimal control of reservoirs. Stoch. Hydrol. Hydraul. 1987, 1, 169–184. [49] Mezenner, N.; Dechemi, N.; Bermad, A.; Benkaci, T. Optimized reservoir operation using genetic algorithm and simulated inflows to reservoir based principal components analysis: The case of Cheffia reservoir—Algeria. Model. Earth Syst. Environ. 2023. [50] Chandra, V.S.S.; Hareendran, S.A.; Sankar, S.S. Optimal reservoir optimization using multiobjective genetic algorithm. In Advances in Swarm Intelligence. I.C.S.I. 2020; Tan, Y., Shi, Y., Tuba, M., Eds.; Lecture Notes in Computer Science 12145; Springer: Cham, Switzerland, 2020.

Copyright

Copyright © 2024 Dr. Bashir Ahmad Pandit. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.