Optical Fiber Bragg Grating as a Strain Sensor

Abstract

The sensor technology industry has come to recognize and value the optical fibre sensor (OFS). It is frequently used to detect changes in the environment and to respond to outputs from other systems, such as those in industrial, monitoring, and chemical analysis applications. While a brief segment of optical fiber with a particular wavelength is reflected with light in a device known as a Fibre Bragg Grating, a Bragg reflector begins to grow and transmit all other wavelengths. Through software modeling, the current study focuses on the changing traits and behaviors of temperature and strain sensors that are used with fiber bragg gratings (FBG). The main objective of this work is to study the properties and behavior of strain sensors utilized in conjunction with fiber bragg gratings. A strain sensor can be used to determine the strain in an object whose resistance changes when force is applied.

Introduction

I. INTRODUCTION

A fiber-optic sensor is one that processes extrinsic sensor signals that are transmitted from the far sensor to the electronics, in addition to acting as an intrinsic sensor. An optical fibre consists of three parts: the coating, the cladding, and the core. The cladding layer was originally made of a dielectric material and has an index of refraction of n2. The index of refraction of the cladding material is less than that of the core material.[1]. sensors made of optical fibre that have a very broad bandwidth, are resilient against electromagnetic interference, and can function well in environments with high pressure, high temperatures, and poisonous materials.[2] The fibre Bragg grating sensor, also called Fibre Bragg Grating, is one of the most intriguing developments in optical fibre sensing technology. It is frequently employed in many SHM paradigms and has the ability to multiplex.[3] A Fibre Bragg Grating is a sensor with a distinct personality to adhere to. For instance, when the fibre is compacted, the strain is calculated using the Fibre Bragg Grating. This is caused by the distortion of the optical fibre, which alters the time adjustment of the microstructure. Affectability of the temperature-sensitive material is also intrinsic to a fibre Bragg grating. The temperature sensor used in the Fibre Bragg Grating, where the thermo-optic coefficient and the thermal-expansion coefficient cause the Bragg wavelength to shift as a result of a change in refractive index, is comparable to the strain sensors to which the single-point sensors belong and preserves the features of small size, solidity, peak accuracy, and elasto-optic (optical strain).[4] Various studies on Fibre Bragg Grating (FBG) have been carried out in the last few years by various researchers who have employed simulation to use Fibre Bragg Grating as a strain and temperature sensor. The refractive index and the grating period are the two primary results of Fibre Bragg Grating. In order to better understand the implications of Fibre Bragg Grating, this study discusses Fibre Bragg Grating and focuses on numerical theoretical demonstration and simulation using MATLAB.

Fibre Bragg Grating (FBG) have shown a great potential advantage in biomedical application over the past ten years [5] due to their prominent characteristics, which include their extremely small size, light weight, immunity to electromagnetic interference (EMI), electrical neutrality, and ability to be easily embedded into a structure without having any effects on the mechanical properties of the object under investigation[6][7].Fibre Bragg Grating was used as a photoacoustic (PA)detection method to detect the existence of tumours because of its capacity to transform the absorbed energy entirely into heat without producing PA signals caused by scattering particles[7]. Because it combines light contrast and ultrasonic resolution, the photoacoustic approach is unique[8]. This technique is used in tumour diagnosis because of its benefits, which include noninvasiveness, high detection sensitivity, and the ability to identify small element sizes[9],[10].

A sensor can be made out of specifically constructed optical fibre. In a tiny portion of the fibre, the core refractive index of the optical fibre intended for sensor applications differs from that of the conventional fibre core and cladding [11]. Usually, a periodic structure is introduced in that tiny portion of the optical fibre core. Fibre Bragg Gratings (FBG) are the name given to this region of the fibre core because it reflects specific wavelengths of light. When a dielectric waveguide's properties are regularly altered, the effective refractive index of the guide is also periodically altered [12],[13]. Alternatively, when a DBR is a structure composed of multiple, alternating layers of materials with variable refractive indices. The Bragg wavelength shift of Fibre Bragg Gratings determines the sensitivity of FBG-based sensors.

Encoded in the fibre core segment, the FBG is a periodic wavelength scale alteration of the refractive index. Bragg gratings reflect light at a particular wavelength that meets the Bragg condition. This reflection in a grating occurs when forward and back propagation modes couple at a specific wavelength [14]. The coupling coefficient of the modes is highest when the specific condition, such as the Bragg condition, between the vectors of the light waves and the vector number of the grating, is satisfied.

                                                                               (1)

the Bragg wavelength, the diffraction order m, the grating period, the core's effective refractive index, and the effective wavelength of light. The working concept of the fibre Bragg grating is shown in Figure 1.

For a single FBG, there are theoretically an infinite number of Bragg wavelengths. The diffraction order Bragg wavelength changes for different values of m, as may be inferred from equation (1). In actuality, only one or occasionally two Bragg resonance wavelengths are used because there is a large spectral gap between the two. The second Bragg wavelength of the grating will be twice as short, at 750 nm, assuming the first one, m=1550 nm, is 1550 nm. However, the spectral range of the sources utilised for fibre is usually limited to 100 nm. Additional Bragg peaks may show up if the refractive index modulation in FBG is not sinusoidal, as it usually is. This technique is used in tumour diagnosis because of its benefits, which include noninvasiveness, high detection sensitivity, and the ability to identify small element sizes[9],[10]. This technique is used in tumour diagnosis because of its benefits, which include noninvasiveness, high detection sensitivity, and the ability to identify small element sizes[9],[10].

II. THE FUNDAMENTALS OF FBG SENSING PRINCIPLE

Figure 1 illustrates the Fibre Bragg Grating (FBG), a single mode fibre with periodic refractive index modulation along its core. The reflecting index of the fibre core increases in a single mode optical fibre exposed to strong UV radiation, resulting in a fixed index modulation called a grating[12]. The wavelength that is reflected when the FBG is exposed to a specific wavelength is known as the Bragg's wavelength, or maximum reflectivity, since the period of the grating area is roughly half that of the input light's wavelength, as indicated in equation (2) [4][6][11].

                                                                                                          (2)

where neff is the effective refractive index of the fibre core, Λ is the FBG period, and λB is the Bragg grating wavelength in the free-space centre wavelength of the input light that will be back-reflected from the FBG. The fibre also transmits the remaining portion of the light.

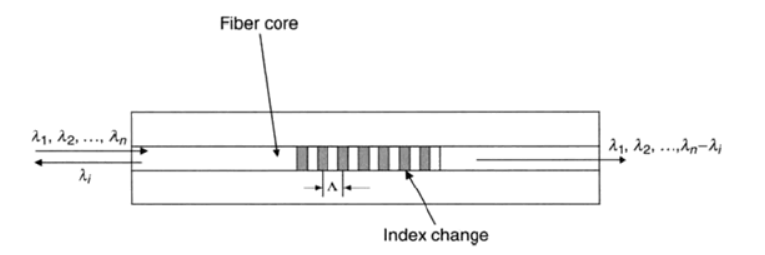
Figure 1: Schematic diagram of a fiber Bragg grating. [17]

Temperature and strain are the two variables in (1) that are sensitive to variations in the outside environment.These parameters are the grating period Λ, the effective index of the core, and the neff. The effective index is affected by temperature variations due to the thermo-optic effect, whereas the period is affected by thermal expansion of the glass. Hooke's law explains how the elasto-optic effect and the glass's elasticity cause changes in period and effective index, respectively, when strain is applied. The effective index and period of the grating will move due to strain and temperature variations, changing the overall Bragg wavelength by λB. Therefore, equation (3) will be produced by the Bragg condition:

                         (3)

The last component of the formula can be disregarded since it simply multiplies two little values. After taking (1) into account, we will have the formula for the change in Bragg wavelength:

                                                               (4)

The Bragg wavelength will vary if any of the previously listed characteristics changes. One can determine the modification by comparing the corresponding Bragg wavelength shift with the reference.

                                                                                     (5)

III. REFLECTION AND TRANSMISSION OF LIGHT IN FIBER BRAGG GRATING

The refractive index of the fibre core fluctuates with a period of κ, as seen in the image below.  The portion of light whose wavelength matches that of the fibre The bragg grating will be reflected back to the input end when a broad spectrum light source is discharged into one end of the fibre, allowing the remaining light to pass through to the other end. The following figure provides an explanation of this reflection phenomenon.

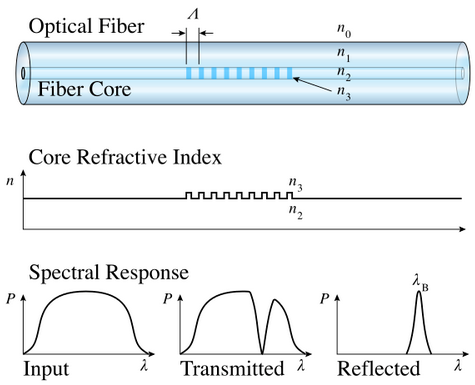
Figure 2 : The reflection and Transmission Spectrum of an FBG. [18]

The following equation results from the Bragg grating condition's requirement for momentum conservation:

                                            (5)

where λB is the wavelength of light reflected by the Bragg grating and neff is the effective refractive index of the fibre core.

Fresnel reflection is the fundamental idea underlying the operation of fibre Bragg gratings (FBGs). when light is allowed to reflect and refract through the combination of two media that have differing refractive indices. Over a given length, the fibre Bragg grating will normally display a sinusoidal fluctuation in refractive index. As demonstrated in Figure 3, the bandwidth, or the range of wavelengths between the initial minima, is determined by Δλ, where δn0 is the variation in the refractive index (n3-n2) and η is the fraction of power in the core.

                                  (6)

IV. WORKING PRINCIPLE OF FIBER BRAGG GRATING

An optical sensor known as an FBG is produced by laterally exposing a single mode fibre core to a strong UV laser light pattern on a regular basis. The exposure causes the refractive index of the fiber's core to grow gradually, resulting in fixed index modulation known as grating spacing. As seen in the image below, the grating inside the fibre optic core is responsible for transmitting all other light while reflecting a particular input light wavelength known as the Bragg wavelength (Bragg related to grating period). We obtain the Bragg wavelength from the equation.

                                                                          (7)

The shift in the reflected Bragg wavelength is detected by an interrogation unit, as shown in the above picture, when a change in physical characteristics occurs and is determined by equation.

(8)

Where pe is the strain-optic coefficient, T is the change in temperature, induced strain, thermal expansion coefficient, and thermo-optic coefficient are all present. According to the equation above, temperature and strain both affect Bragg shift. Pe = 0.22 and various coefficients are known for silica fibre.

V. FBG EQUATIONS FOR STRAIN MEASUREMENT

A sensor's length, or strain, L, varies from its initial length when stress is applied to it. When a stress is applied to the fibre, the associated strain is L/L. Temperature adjustment is required because thermal expansion causes temperature to affect physical dimensions. To measure strain alone when utilising an FBG sensor, the impact of temperature on wavelength shift calculations must be taken out. To counterbalance the effect of local temperature on the FBG, this can be achieved by attaching a temperature sensor to it. Therefore, we have subtracted eq. (10) from eq. (9) to get eq. (5) below in order to measure strain.

            (9)

                                       (10)

where e is the applied axial strain and p is the effective strain-optic constant, represented as

                        (11)

where v is the Poisson's ratio and p1 and p2 are parts of the strain-optic sensor. P1 = 0.113, P2= 0.252, V = 0.16, and N = 1.482 for a germanosilicate optical fibre. As a result, p has the value 0.22.

Bragg wavelength strain sensitivity,

                                                                                                                  (12)

VI. METHODOLOGY

Setting the parameter is one of the most important and critical aspects of the Fibre Bragg Grating simulation. The primary Fibre Bragg Grating parameter in this simulation is set to the default values. Setting the specification parameter where the sensor displays the effect after detecting any changes brought on by variations in temperature and strain are essential.

Table 1: Fundamental Parameters in the Fiber Bragg Grating

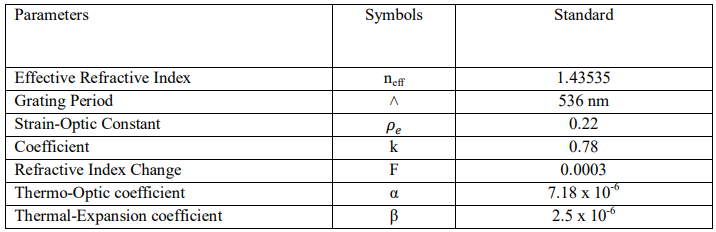
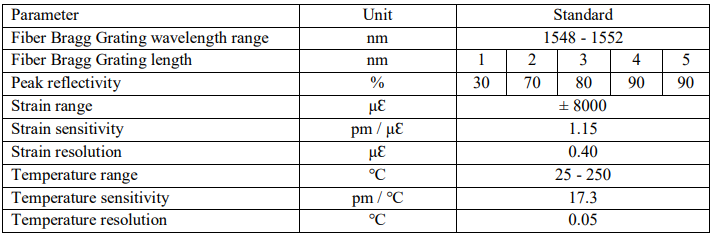
Table 2: Specifications of Parameters in the the Fiber Bragg Grating

VII. RESULTS AND DISCUSSION

The goal of this study on Fibre Bragg Grating simulation is to illustrate the behaviours and properties of the fibre bragg grating for temperature and strain sensors. Bragg wavelength shift variations are regulated by temperature and strain. Under various refractive index changes and grating lengths, the spectrum reflectance of Fibre Bragg Grating sensors varies. The findings of this simulation of Fibre Bragg Grating acting as temperature and strain sensors are shown in the table below. When there is a change in the fiber's length from its initial length, the strain is measured. The fibre detects strain in the fibre when the length of the fibre deviates from its initial length. when a result, strain increases when fibre length changes more dramatically. When ?l = 0.45 was the fibre change, it rose to 272411 µε.

Table 3: Strain imposed by a change in the length of the fibre

Bragg Wavelength Shift: MATLAB may be used to plot the graph of Bragg Wavelength Shift with applied strain, which can be obtained from a table.

Table 4 : The Bragg wavelength shift with applied strain

Figure 1 : Graph of the Bragg wavelength shift versus strain

The spectrum reflectance is dependent on both the grating length and changes in refractive index.

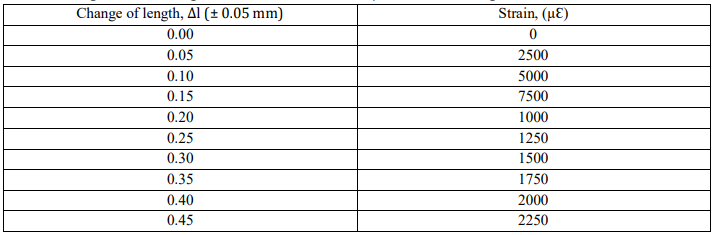
Dependence of Spectral Reflectivity on distinct Refractive Index Changes: A graph representing the spectral reflectivity of Fibre Bragg Grating is displayed against five distinct refractive index changes, namely = 0.0003, 0.0005, 0.0008, 0.0012, and 0.0015. Research has demonstrated that there are distinct changes in refractive index that affect the reflectivity of Fibre Bragg Grating. When the refractive index changes, spectral reflectivity rises. At a grating length of 1.0 mm, it rises to 99.09% with ?n = 0.0015.

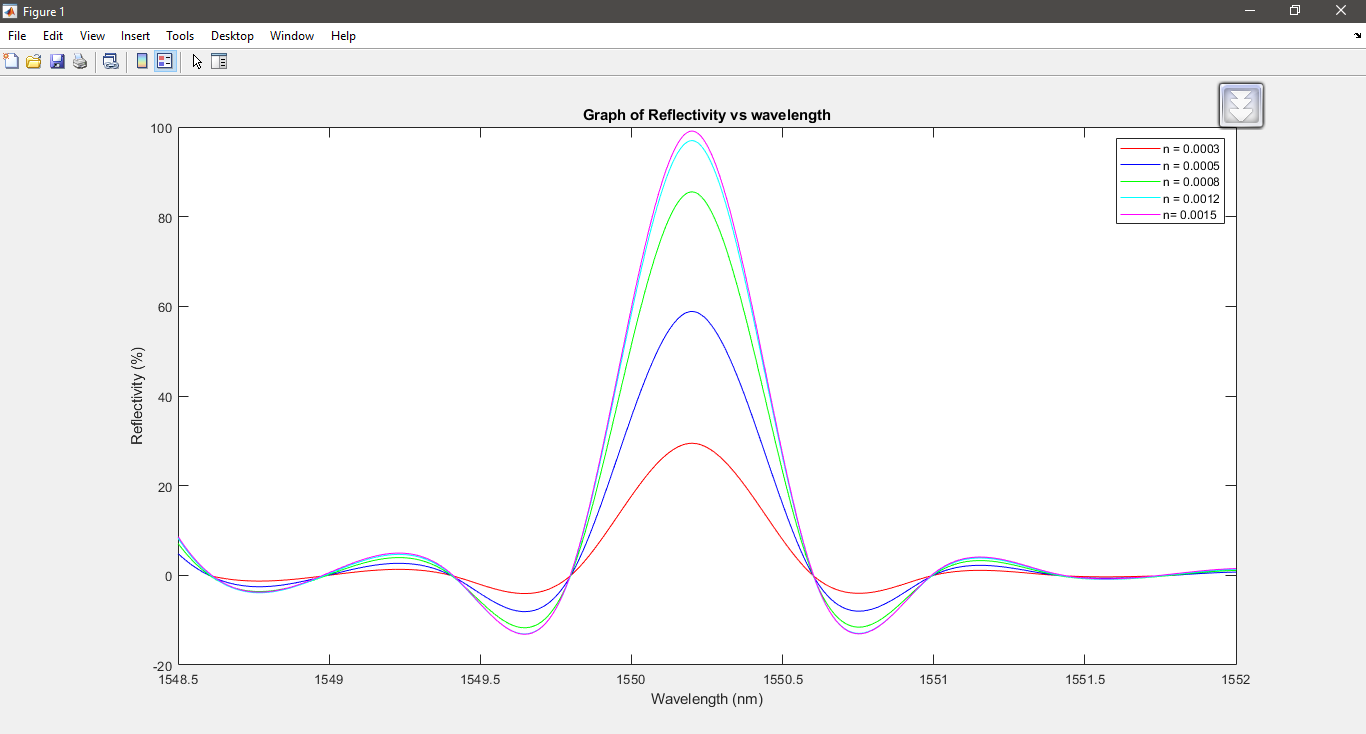
At grating length L = 1mm, the reflection spectrum of Fibre Bragg Grating with varying refractive indices changes.

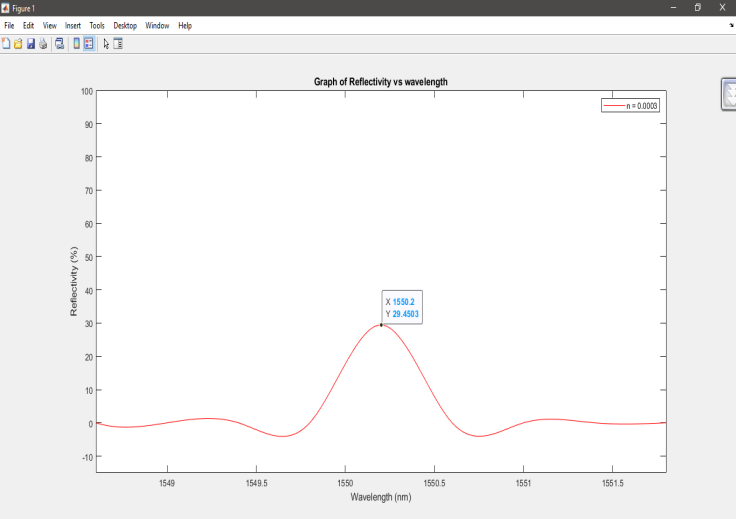
The Fibre Bragg reflection spectrum Grating with peak reflectivity of R = 29.45% and refractive index change of ?n = 0.0003 at grating length of L = 1 mm

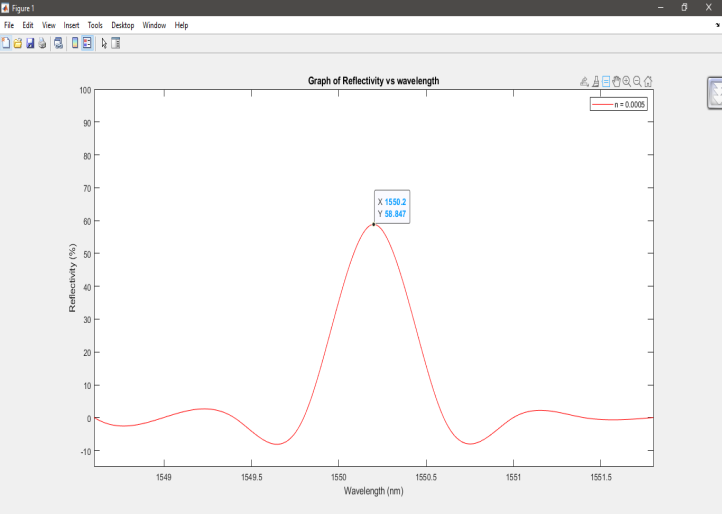
Fibre Bragg's reflection spectrum Grating with peak reflectivity of R = 58.85% and refractive index change of ?n = 0.0005 at grating length of L = 1 mm

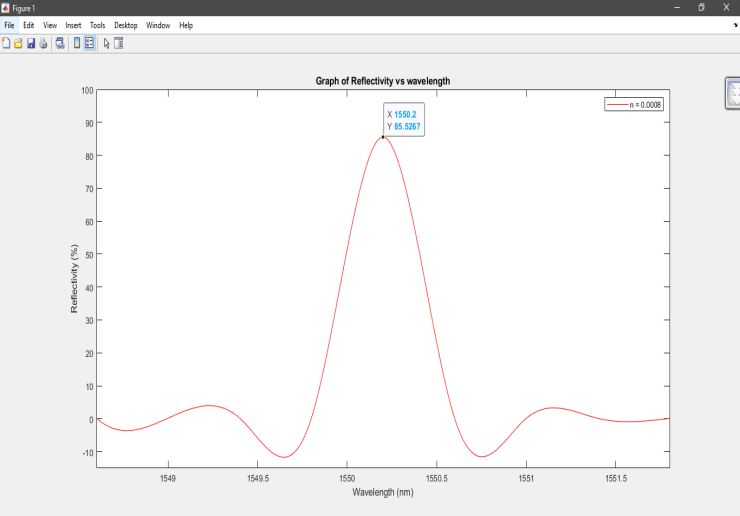
The Fibre Bragg reflection spectrum Grating with peak reflectivity of R = 85.53% and refractive index change of ?n = 0.0008 at grating length of L = 1 mm

The Fibre Bragg reflection spectrum Grating with peak reflectivity of R = 96.95% and refractive index change of ?n = 0.0012 at grating length of L = 1 mm

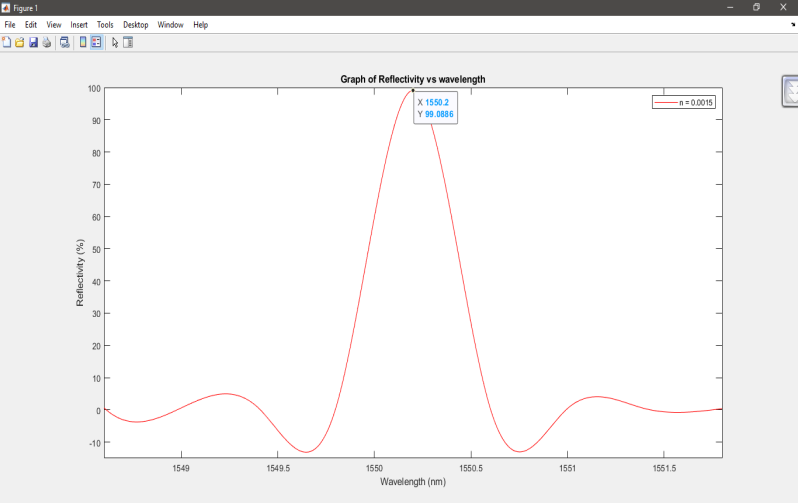
The Fibre Bragg reflection spectrum Grating with peak reflectivity of R = 99.09% and refractive index variation of ?n = 0.0015 at grating length L = 1 mm

Conclusion

In conclusion , this study has successfully accomplished every one of its stated goals. This study suggested simulating the behaviours and properties of fibre bragg gratings as temperature and strain sensors. This simulation can be used to examine performance, identify traits and behaviour, and assess how well the temperature and strain sensors work. The current work for this simulation created model for the temperature and strain sensors in the Fibre Bragg Grating was successfully analysed using MATLAB. The strain and temperature sensors of the Fibre Bragg Grating sensing system were simulated and coded for this research project using MATLAB software. This simulation can be used to analyse the behaviour, characteristics, and performance of fibre bragg gratings. Among the properties are the strain, temperature, and spectrum reflectivity for varying refractive index changes as well as grating length. The variations in grating length and refractive index were used in this simulation to examine these traits and behaviours.According to the simulation, strain is produced when a fiber\'s length deviates from its initial length. In the simulation, the increase in strain has an impact on the increase in Bragg wavelength shift.

References

[1] Fidanboylu, K. A., & Efendioglu, H. S. (2009, May). Fiber optic sensors and their applications. In 5th International Advanced Technologies Symposium (IATS’09) (Vol. 6, pp. 2-3) [2] Sidek, O., & Afzal, M. H. B. (2011, September). A review paper on fiber-optic sensors and application of PDMS materials for enhanced performance. In 2011 IEEE Symposium on Business. Engineering and Industrial Applications (ISBEIA) (pp. 458-463). IEEE. [3] Ye, X. W., Ni, Y. Q., & Yin, J. H. (2013). Safety monitoring of railway tunnel construction using Fiber Bragg Grating sensing technology. Advances in Structural Engineering, 16(8), 1401-1409 [4] E. Al-Fakih, N. A. Abu Osman, and F. R. Mahamd Adikan, “The Use of Fiber Bragg Grating Sensors in Biomechanics and Rehabilitation Applications: The State-of-the-Art and Ongoing Research Topics,” Sensors, vol. 12, no. 12, pp. 12890–12926, 2012. [5] T. Fink, Q. Zhang, W. Ahrens, and M. Han, “Study of ?-phase-shifted, fiber Bragg gratings for ultrasonic detection,” Fiber Opt. Sensors Appl. IX, vol. 8370, no. 7, pp. 1–7, 2012. [6] G. Wild and S. Hinckley, “Optical Fibre Bragg Gratings for Acoustic Sensors,” Int. Congr. Acoust., no. August, pp. 1–7, 2010. [7] A. Yarai and T. Nakanishi, “Fiber Bragg grating applied pulsed photoacoustic detection technique for online monitoring concentration of liquid,” J. Acoust. Soc. Am., vol. 123, no. 5, p. 3285, 2008. [8] C. Li and L. V Wang, “Photoacoustic tomography and sensing in biomedicine,” Phys. Med. Biol., vol. 54, no. 19, pp. R59–R97, 2009. [9] M. Xu and L. V. Wang, “Photoacoustic imaging in biomedicine,” Rev. Sci. Instrum., vol. 77, no. 4, p. 041101, 2006. [10] J. Xia, J. Yao, and L. V Wang, “Photoacoustic Tomography?: Principles and Advances,” Prog. eletromagnic Res., vol. 147, no. May, pp. 1–22, 2014. [11] E.Udd, Fiber Optic Sensors: An Introduction for Engineerings and Scientists (John Wiley and Sons, New York, 1991). [12] A.Cusano, A. Cutolo and M. Giordano, “Fiber Bragg Gratings Evanescent Wave Sensors: A View Back and RecentAdvancements”, Sensors, Springer-Verlag Berlin Heidelberg, 2008. [13] K.O.Hill and G. Meltz, “Fiber Bragg Grating Technology Fundamentals and Overview”, Journal of Lightwave Technology, Vol. 15,No. 8, August 1997. [14] G.P. Agrawal, Fiber-Optic Communication Systems, (John Wiley & Sons, 2002). [15] P. Fomitchov and S. Krishnaswamy, “Response of a fiber Bragg grating ultrasonic sensor,” Opt. Eng., vol. 42, no. 4, pp. 956–963, 2003. [16] M. A. Othman, M. M. Ismail, H. A. Sulaiman, et.al., “An Analysis of 10 Gbits / s Optical Transmission System using Fiber Bragg Grating ( FBG ),” IOSR J. Eng., vol. 2, no. 7, pp. 55–61, 2012. [17] https://www.fiberoptics4sale.com/blogs/archive-posts/95046406-what-is-fiber-bragg-grating [18] https://en.wikipedia.org/wiki/Fiber_Bragg_grating

Copyright

Copyright © 2024 Muhammad Arif Bin Jalil. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.