Optical Fiber Bragg Grating As A Temperature Sensor

Abstract

The optical fibre sensor (OFS) has become quite well-known and prominent in the sensor technology industry. It is often used to react to outputs from other systems, like those in industrial, monitoring, and chemical analysis applications, and to detect changes in the environment. A Fibre Bragg Grating (FBG) is a device that allows light to be reflected from a short section of optical fiber at a specific wavelength, while the Bragg reflector expands and transmits all other wavelengths. The current effort focuses on the evolving characteristics and behaviors of strain and temperature sensors operating on fiber bragg gratings through computer modeling. The temperature sensor is employed to detect and quantify any variations in temperature on the Fiber Bragg Grating that could result in accidents or fires. This will show how the Fibre Bragg Grating may be used to showcase temperature sensors.

Introduction

I. INTRODUCTION

A fiber-optic sensor is one that uses optical fibre both as an intrinsic sensor and as a method of processing extrinsic sensor signals that are relayed from the far sensor to the electronics. The three components of an optical fibre are the coating, cladding, and core. The cladding layer has an index of refraction of n2 , and it was initially composed of a dielectric substance. The cladding material's index of refraction is lower than the core material's.[1]. Optical fibre sensors with a very wide bandwidth, resilience to electromagnetic interference, and a robust ability to operate in harsh temperature, toxic, and pressure situations.[2] One of the most interesting advancements in optical fibre sensing technology is the fibre Bragg grating (also known as fibre Bragg Grating) sensor, which has multiplexing capacity and is widely used in a variety of SHM.[3] A Fibre Bragg Grating functions as a sensor and has a unique character to follow. For example, the strain is determined by the Fibre Bragg Grating when the fibre is compacted. This occurs as a result of the optical fibre distortion, which modifies the microstructure's time adjustment. For a fibre Bragg grating, affectability of the temperature-sensitive material is also inherent. The temperature sensor acting in the Fibre Bragg Grating, where the Bragg wavelength shifted due to the change in refractive index is induced by the thermo-optic coefficient and the thermal-expansion coefficient, is similar to the strain sensors where the single-point sensors belong to and save the highlights the characteristics of small size, solidness, peak accuracy, and elasto-optic for the optical strain.[4] In the past several years, numerous studies have been conducted on Fibre Bragg Grating (Fibre Bragg Grating) by numerous researchers who have used simulation to use Fibre Bragg Grating as a strain and temperature sensor. The two main outcomes of Fibre Bragg Grating are the refractive index and the grating period. This study presents Fibre Bragg Grating and centres on its numerical theoretical demonstration and simulation using MATLAB, aided by simulation results that provide insight into the impacts of Fibre Bragg Grating.

Fibre Bragg Grating (FBG) have shown a great potential advantage in biomedical application over the past ten years [5] due to their prominent characteristics, which include their extremely small size, light weight, immunity to electromagnetic interference (EMI), electrical neutrality, and ability to be easily embedded into a structure without having any effects on the mechanical properties of the object under investigation[6][7].Fibre Bragg Grating was used as a photoacoustic (PA)detection method to detect the existence of tumours because of its capacity to transform the absorbed energy entirely into heat without producing PA signals caused by scattering particles[7]. Because it combines light contrast and ultrasonic resolution, the photoacoustic approach is unique[8]. This technique is used in tumour diagnosis because of its benefits, which include noninvasiveness, high detection sensitivity, and the ability to identify small element sizes[9],[10].

Optical fibre that has been specially designed can be used to create sensors. The core refractive index of the optical fibre meant for sensor applications is different from the core and cladding of a conventional fibre only a very small fraction of the fibre [11]. Usually, in that little area of the optical fibre core, a periodic structure is inserted. This part of the fibre core is called Fibre Bragg Gratings (FBG) because it reflects particular light wavelengths. The effective refractive index of a dielectric waveguide is periodically changed when the waveguide's characteristics are changed on a regular basis [12], [13]. On the other hand, a DBR is a structure made up of several alternating layers of materials with different refractive indices. The FBG, which is a periodic wavelength-scale modification of the refractive index, is encoded in the fibre core segment. Light that satisfies the Bragg condition at a specific wavelength is reflected by Bragg gratings. When forward and back propagation modes couple at a particular wavelength, a grating experiences this reflection [14]. When a particular requirement, such as the Bragg condition, between the vectors of the light waves and the vector number of the grating is met, the coupling coefficient of the modes is at its highest:

  (1)

the Bragg wavelength, the diffraction order m, the grating period, the core's effective refractive index, and the effective wavelength of light. The working concept of the fibre Bragg grating is shown in Figure 1.

There is an infinite number of possible Bragg wavelengths for a single FBG. Equation (1) suggests that for a given value of m, the diffraction order Bragg wavelength varies. In fact, due to a huge spectral difference between the two, only one or sometimes two Bragg resonance wavelengths are used. Assuming the first Bragg wavelength, m=1550 nm, is 1550 nm, the second Bragg wavelength of the grating will be twice as short, at 750 nm. Nevertheless, the sources used for fibre typically have a spectral range of only 100 nm. If the refractive index modulation in FBG is not sinusoidal, as it normally is, then additional Bragg peaks could appear. For instance, the Fourier spectrum of a rectangular grating has many modulation frequencies, which can lead to multiple Bragg peaks. despite the fact that most fiber-based gratings have essentially sinusoidal index modulation. There are several FBG structures; however, the experiment and analysis in this paper used a uniform FBG to test how well an FBG functions as a sensor.Extra Bragg peaks may show up if the refractive index modulation in FBG is not sinusoidal as it usually is. For example, a rectangular grating's Fourier spectrum contains a large number of modulation frequencies, which can result in several Bragg peaks, even though the index modulation of the majority of fiber-based gratings is essentially sinusoidal. Although there are several FBG structures, the experiment and analysis in this work tested the sensor performance of an FBG using a uniform FBG.

II. THE FUNDAMENTALS OF FBG SENSING PRINCIPLE

The Fibre Bragg Grating (FBG) is a single mode fibre having periodic refractive index modulation along its core, as seen in figure 1. When a single mode optical fibre is subjected to intense UV radiation, the reflective index of the fibre core rises, creating a fixed index modulation known as a grating[9]. Since the period of the grating area is approximately half that of the wavelength of the input light, as shown in equation (2) [4][6][11], the wavelength that is reflected when the FBG is subjected to a particular wavelength is known as the Bragg's wavelength, or maximum reflectivity.

                                                                                                 (2)

where Λ is the FBG period, λB is the Bragg grating wavelength in the free-space centre wavelength of the input light that will be back-reflected from the FBG, and neff is the effective refractive index of the fibre core. The remaining fraction of the light is likewise transmitted by the fibre.

Figure 1: Schematic diagram of a fiber Bragg grating. [17]

Two quantities in (1), namely temperature and strain, are susceptible to changes in external conditions.Effective index of the core ,neff  and grating period  Λ are these parameters. When the temperature varies, the thermo-optic effect causes the effective index to change, whilst the glass thermal expansion causes the period to vary. When strain is applied, effective index changes as a result of the elasto-optic effect, whereas period changes as a result of the glass's elasticity, both of which are explained by Hooke's law. The overall Bragg wavelength will change by λB as a result of the effective index and period of the grating shifting as a result of strain and temperature changes. Therefore, the Bragg condition will produce an equation (3):

                    (3)

Since the final part of the formula represents the multiplication of two little amounts, it can be ignored. We shall arrive at the formula for the change of Bragg wavelength after including accounting for (1):

                                                 (4)

If any of the previously mentioned parameters changes, the Bragg wavelength will also change. By contrasting the related Bragg wavelength shift with the reference, one may identify the alteration.

III. REFLECTION AND TRANSMISSION OF LIGHT IN FIBER BRAGG GRATING

As observed in the below image, the refractive index of the fibre core varies with a period of . Λ  The part of light whose wavelength coincides with the fiber wavelength When a broad spectrum light source is discharged into one end of the fibre, the remaining light will pass through to the other end, and the bragg grating will be reflected back to the input end. This reflection phenomena is explained in the diagram that follows.

Figure 2 : The reflection and Transmission Spectrum of an FBG. [18]

The necessity of momentum conservation in the Bragg grating condition leads to the following equation:

                                           (5)

where neff is the effective refractive index of the fibre core and λB is the wavelength of light reflected by the Bragg grating.

The basic principle behind the functioning of fibre Bragg gratings (FBGs) is Fresnel reflection. when two mediums with different refractive indices come together and allow light to reflect and refract. The fibre Bragg grating will typically show a sinusoidal variation in refractive index over a specified length. As seen in Figure 3, Δλ, where δn0 is the fluctuation in the refractive index (n3-n2) and η is the fraction of power in the core, determines the bandwidth, or the distance in wavelengths between the first minima.

                                                          (6)

A. Working Principle of Fiber Bragg Grating

A single mode fibre core is regularly exposed laterally to a powerful UV laser light pattern, creating an optical sensor called an FBG. The fiber's core's refractive index steadily increases as a result of the exposure, producing fixed index modulation known as grating spacing. The grating within the fibre optic core, as shown in the image below, is in charge of transmitting all other light while reflecting a certain input light wavelength that is referred to as the Bragg wavelength (Bragg related to grating period). Using the equation, we can determine the Bragg wavelength.

                                                                                                   (7)

When a change in physical features occurs, an interrogation unit, as depicted in the above picture, detects the shift in the reflected Bragg wavelength, which is determined by equation.

                     (8)

Where pe is the strain-optic coefficient, T is the change in temperature, induced strain, thermal expansion coefficient, and thermo-optic coefficient are all present. According to the equation above, temperature and strain both affect Bragg shift. Pe = 0.22 and various coefficients are known for silica fibre.

B. FBG Equations for Temperature Measurement

The Bragg wavelength shift is given by the following equation.

                          (9)

                                           (10)

For fused Silica,

                                                             (11)

                                                                   (12)

Bragg wavelength temperature sensitivity,

                                                                                                                                    (13)

IV. METHODOLOGY

One of the most crucial and significant parts of the Fibre Bragg Grating simulation is setting the parameter. In this simulation, the main Fibre Bragg Grating parameter is left at its default settings. However, it is crucial to set the specification setting where the sensor shows the effect only after identifying any changes caused by strain and temperature differences.

Table 1: Fundamental Parameters in the Fiber Bragg Grating

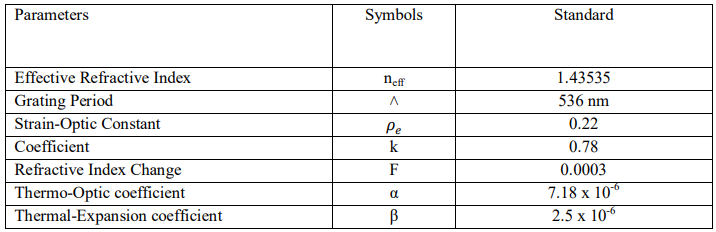
Table 2: Specifications of Parameters in the the Fiber Bragg Grating

V. RESULTS AND DISCUSSION

The temperature increase are used to measure the Bragg wavelength shift. If temperature variations rise, the Bragg wavelength shift indicates an increase. When the Bragg wavelength shift continues to climb until 12.48745, the temperature change increased to 250 °C.

Table 5: Temperature Change with a Bragg Wavelength Shift

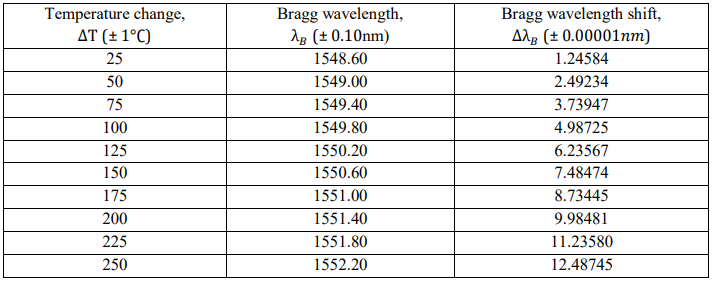
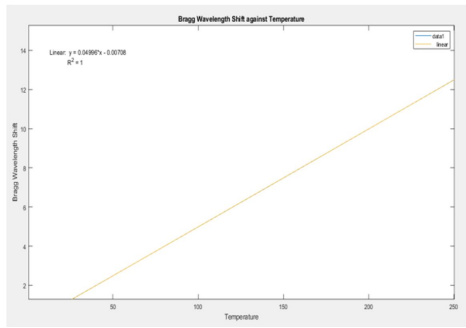
Figure 3 : Graph Temperature against Bragg Wavelength Shift

A. Spectral Reflectivity dependence on various Grating Length

A graph showing the dependency of spectral reflectivity on various grating lengths, L = 1mm, 2mm, 3mm, 4mm, and 5mm, is displayed. The outcome displays how the spectral reflectivity varies for L = 1 mm, 2 mm, 3 mm, 4 mm, and 5 mm grating lengths, while the changes in the refractive index were fixed at ?n = 0.0003. The reflectance increased as the grating length increased. When the refractive index changes were set to remain constant at ?n = 0.0003, the spectrum reflectivity increased to 99.08% when the grating length increased to 5mm.

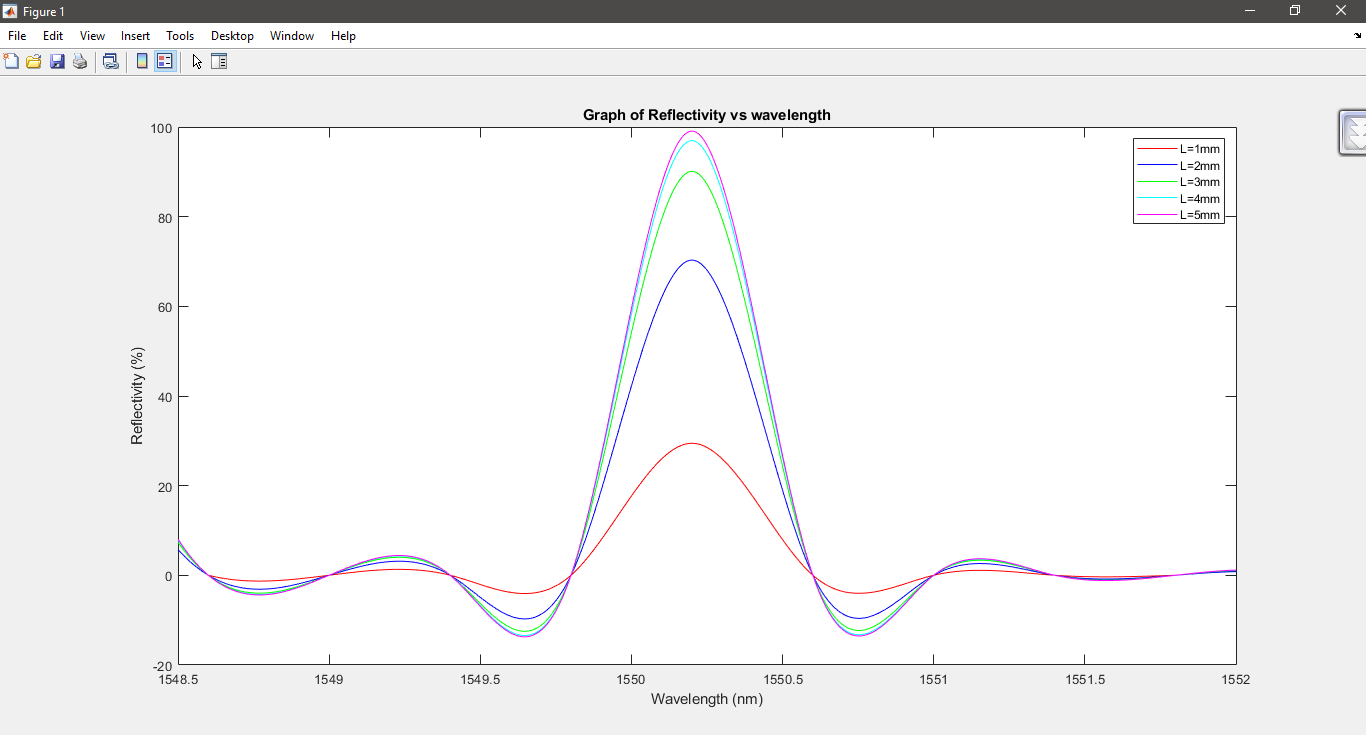
Figure 4: The Fiber Bragg Grating reflection spectrum with a refractive index shift of ?n = 0.0003 with varying grating lengths

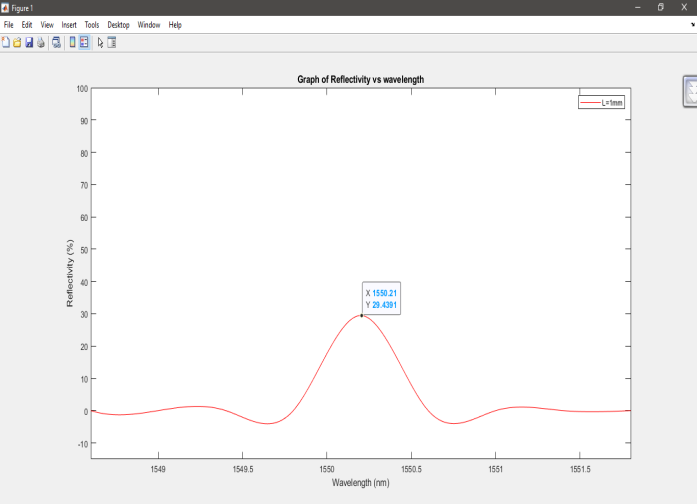
Figure 5: The reflection spectrum of Fiber Bragg Grating with grating length, L = 1mm at refractive index change of ?n = 0.0003 with peak reflectivity, R = 29.44%

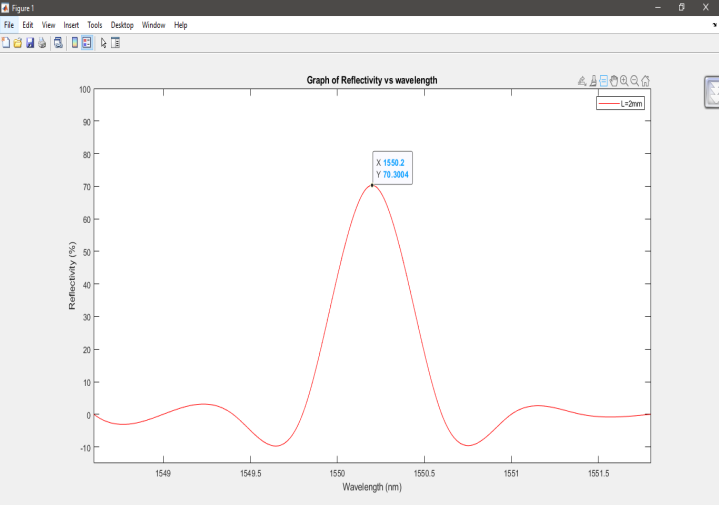
Figure 6: The Fiber Bragg reflection spectrum grating having a peak reflectivity of R = 70.31% and a grating length of L = 2 mm at a refractive index variation of ?n = 0.0003.

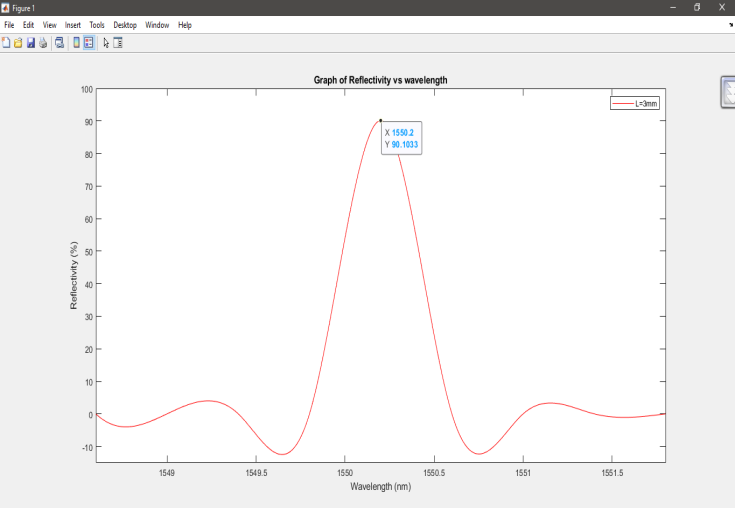
Figure 7: The Fiber Bragg reflection spectrum grating with a peak reflectivity of R = 90.10 percent and a grating length of L = 3 mm at a refractive index variation of ?n = 0.0003.

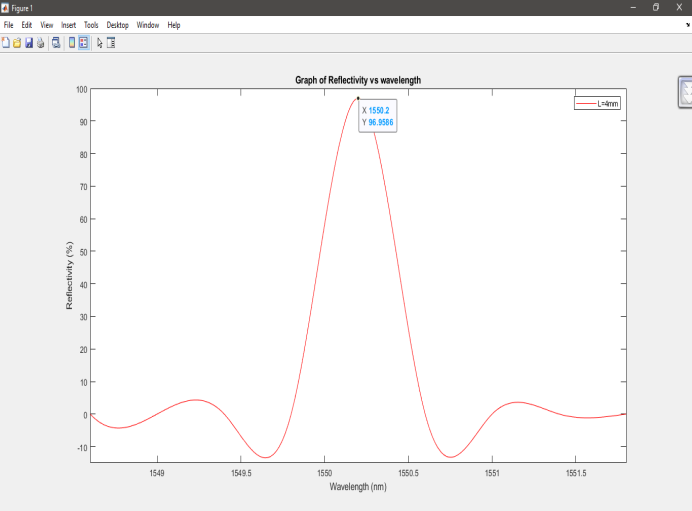
Figure 8: The reflection spectrum of Fiber Bragg Grating with grating length, L = 4mm at refractive index change of ?n = 0.0003 with peak reflectivity, R = 96.96%

Figure 9: The Fiber Bragg reflection spectrum grating with a peak reflectivity of R = 99.08% and a grating length of L = 5mm at a refractive index change of ?n = 0.0003.

Conclusion

In conclusion, all of the objectives of this study have been successfully met. In order to simulate temperature sensors, this study proposed modeling the characteristics and behaviors of fiber bragg gratings. Performance analysis, trait and behavior identification, and the evaluation of the temperature sensor functionality can all be done with this simulation. MATLAB was successfully used to analyze the current work for this simulation-designed model for the temperature sensors in the Fiber Bragg Grating. For this study, MATLAB software was used to simulate the spectral characteristics for temperature sensors of the Fiber Bragg Grating sensing system. The behavior, features, and functionality of Fiber Bragg Gratings can be examined with this simulation. The same for temperature, which in this study is simulated linearly. The temperature will be affected by the Bragg wavelength shift, as the Bragg wavelength shift increases, so does the temperature.

References

[1] Fidanboylu, K. A., & Efendioglu, H. S. (2009, May). Fiber optic sensors and their applications. In 5th International Advanced Technologies Symposium (IATS’09) (Vol. 6, pp. 2-3) [2] Sidek, O., & Afzal, M. H. B. (2011, September). A review paper on fiber-optic sensors and application of PDMS materials for enhanced performance. In 2011 IEEE Symposium on Business. [3] Engineering and Industrial Applications (ISBEIA) (pp. 458-463). IEEE. Ye, X. W., Ni, Y. Q., & Yin, J. H. (2013). Safety monitoring of railway tunnel construction using Fiber Bragg Grating sensing technology. Advances in Structural Engineering, 16(8), 1401-1409 [4] E. Al-Fakih, N. A. Abu Osman, and F. R. Mahamd Adikan, “The Use of Fiber Bragg Grating Sensors in Biomechanics and Rehabilitation Applications: The State-of-the-Art and Ongoing Research Topics,” Sensors, vol. 12, no. 12, pp. 12890–12926, 2012. [5] T. Fink, Q. Zhang, W. Ahrens, and M. Han, “Study of ?-phase-shifted, fiber Bragg gratings for ultrasonic detection,” Fiber Opt. Sensors Appl. IX, vol. 8370, no. 7, pp. 1–7, 2012. [6] G. Wild and S. Hinckley, “Optical Fibre Bragg Gratings for Acoustic Sensors,” Int. Congr. Acoust., no. August, pp. 1–7, 2010. [7] A. Yarai and T. Nakanishi, “Fiber Bragg grating applied pulsed photoacoustic detection technique for online monitoring concentration of liquid,” J. Acoust. Soc. Am., vol. 123, no. 5, p. 3285, 2008. [8] C. Li and L. V Wang, “Photoacoustic tomography and sensing in biomedicine,” Phys. Med. Biol., vol. 54, no. 19, pp. R59–R97, 2009. [9] M. Xu and L. V. Wang, “Photoacoustic imaging in biomedicine,” Rev. Sci. Instrum., vol. 77, no. 4, p. 041101, 2006. [10] J. Xia, J. Yao, and L. V Wang, “Photoacoustic Tomography?: Principles and Advances,” Prog. eletromagnic Res., vol. 147, no. May, pp. 1–22, 2014. [11] E.Udd, Fiber Optic Sensors: An Introduction for Engineerings and Scientists (John Wiley and Sons, New York, 1991). [12] A.Cusano, A. Cutolo and M. Giordano, “Fiber Bragg Gratings Evanescent Wave Sensors: A View Back and RecentAdvancements”, Sensors, Springer-Verlag Berlin Heidelberg, 2008. [13] K.O.Hill and G. Meltz, “Fiber Bragg Grating Technology Fundamentals and Overview”, Journal of Lightwave Technology, Vol. 15,No. 8, August 1997. [14] G.P. Agrawal, Fiber-Optic Communication Systems, (John Wiley & Sons, 2002). [15] P. Fomitchov and S. Krishnaswamy, “Response of a fiber Bragg grating ultrasonic sensor,” Opt. Eng., vol. 42, no. 4, pp. 956–963, 2003. [16] M. A. Othman, M. M. Ismail, H. A. Sulaiman, et.al., “An Analysis of 10 Gbits / s Optical Transmission System using Fiber Bragg Grating ( FBG ),” IOSR J. Eng., vol. 2, no. 7, pp. 55–61, 2012. [17] https://www.fiberoptics4sale.com/blogs/archive-posts/95046406-what-is-fiber-bragg-grating [18] https://en.wikipedia.org/wiki/Fiber_Bragg_grating

Copyright

Copyright © 2024 Muhammad Arif Bin Jalil. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.