Optimizing Visual Sensor Node Image Compression for Resource-Constrained Environments

Abstract

An Approximate hybrid multiplier design is proposed to reduce the data-path width of lifting 2-D discrete wavelet transform (DWT) especially for wireless visual sensor node applications. The proposed multiplier design takes multiplier operand of size less by 3 bit and calculates full-width outputs with marginal loss of accuracy, which is significant. The proposed approximate 2-D DWT structure uses data-path DWT levels and produces reconstructed color images higher than the 70-dB peak-signal-to-noise ratio (PSNR). Compared with the existing fractional wavelet transform (FrWT)-based 2D DWT structures, the proposed structure has a smaller data-path width and free from overhead. Compared with the existing parallel structure based on hybrid approximate radix-4 and radix-8 encoded Booth multiplier, the proposed approximate structure involves nearly 23% less ADP and 22% less EPI and calculates output images with nearly (4–7)-dB higher PSNR.

Introduction

I. INTRODUCTION

The Visual sensor nodes are the part of wireless visual sensor network (WVSN) and Internet-of-Things (IoT) network, which are used in several interesting applications, such as security, surveillance, healthcare, traffic management, wildlife monitoring, automatic assistance and monitoring of elderly persons, and many more. Availability of low-cost CMOS cameras has created the opportunity to build low-cost visual sensor network (VSN) platforms that are able to capture, process, and disseminate visual data collectively... Visual sensor nodes have a very small memory, typically 64 kB or lesser.

In general, Therefore, the encoder design is highly constrained by resource and timing. A typical image coder consists of three computing blocks. The image transform followed by quantization and coding block. Discrete wavelet transform (DWT) is mostly preferred over the discrete cosine transform (DCT) due to higher compression ratio, multiresolution signal analysis features, and relatively lower computational complexity. DWT structure. In the proposed scheme, we have considered data-path optimization using an approximation technique to reduce ON-chip memory complexity without any overhead. The main contributions of this article are as follows are A design scheme is proposed based on the computational complexity analysis of FrWT and lifting 2-D DWT structures.  Fixed-point simulation lifting 2-D DWT is performed to optimize data-path width of different decomposition levels, which plays an important role on hardware efficiency of 2-D DWT structures and output image quality. Proposed novel approximate hybrid Booth multiplier design using radix-4 and radix-16 encoding that uses operand less by 3 bit  calculates full-width outputs with marginal loss of accuracy. A hardware-efficient approximate parallel lifting 2-D DWT structure  proposed for visual sensor node applications..

A. Overview of DWT

Discrete Wavelet Transform (DWT). Due to its excellent de correlation, energy compaction, and symmetry properties, the DCT has been widely adopted in image and video coding standards, such as JPEG, MPEG-2, H.264, and HEVC. The DCT is generally applied on image blocks, thereby reducing the required memory, but coding block-based DCT coefficients at very low bit-rates the conventional DWT computation method requires the complete image to be kept in memory which is challenging for memory-constrained devices, These low-cost mass-market consumer devices have only limited memory. Moreover, there are many imaging oriented applications, such as visual sensors with very limited on-board memory

B. Characteristics of DWT

The Discrete Wavelet Transform (DWT) is a mathematical tool used for signal processing and data compression. Some of its characteristics include: Multi resolution analysis: DWT decomposes a signal into different frequency components at different resolutions, allowing for analysis at multiple scales. Time-frequency localization: It provides both time and frequency localization, meaning it can accurately detect transient events in signals. Sparse representation: DWT often leads to a sparse representation of signals, which is useful for compression and demonizing applications. Orthogonality: time applications. Applications: DWT is widely used in image and signal processing, including compression, demonizing, feature extraction, and pattern recognition.To sort the tomatoes our proposed system uses two TCS3200 colour sensors which are cost effective and identify the colour dependent on the recurrence examination of the yield. Our proposed system aims to develop a simple, efficient and affordable tomato sorting machine which helps us to get good quality ripe tomatoes without any human error. Further the exhibited paper talks about the current writing of tomato sorting machines in Section II. In Segment III, the design of the proposed framework alongside the equipment and programming utilized are examined in detail. In segment IV, execution of the proposed framework is talked about lastly in segment V, the outcomes alongside its cost investigation are displayed. Area VI finishes up the work with its future extension.

C. Visual Sensor Networks

Visual sensor networks are based on several diverse research fields, including image/vision processing, communication and networking, and distributed and embedded system processing. Thus, the design complexity involves finding the best tradeoff between performance and different aspects of these networks. According to Hengstler and Achaean the design of a camera-based network involves mapping application requirements to a set of network operation parameters that are generally related to several diverse research fields, including network topology, sensing, processing, communication, and resource utilization.

D. Classification Of DWT

Biorthogonal Wavelets: Biorthogonal wavelets do not necessarily have symmetric wavelet functions. They use two sets of wavelet functions: one for decomposition (analysis) and the other for reconstruction (synthesis).

Biorthogonal wavelets offer more flexibility compared to orthogonal wavelets, as they allow for asymmetric wavelets and better adaptation to specific signal characteristics. They are commonly used in applications where perfect reconstruction is not required, such as in loss compression or demising, where preserving certain signal features is more important than perfect reconstruction

1. Data Storage System

The cameras generate large amounts of data over time, which in some cases should be stored for later analysis. An example is monitoring of remote areas by a group of camera nodes, where the frequent transmission of captured image data to a remote sink would quickly exhaust the cameras' energy resources. Thus, in these cases the camera nodes should be equipped with memories of larger capacity in order to store the data. To minimize the amount of data that requires storage, the camera node should classify the data according to its importance by using spatiotemporal analysis of image frames, and decide which data should have priority to be stored. For example, if an application is interested in information about some particular object, then the background can be highly compressed and stored, or even completely discarded. The stored image data usually becomes less important over time, so it can be substituted with newly acquired data. In addition, reducing the redundancy in the data collected by cameras with overlapped views can be achieved via local communication and processing. This enables the cameras to reduce their needs for storage space by keeping only data of unique image regions. Finally, by increasing the available memory, more complex processing tasks can be supported on-board, which in return can reduce data transmissions and reduce the space needed for storing processed data.

2. Signal Processing

Obtaining precise information about the cameras' locations and orientations is crucial for many vision processing algorithms in visual sensor networks. Information on a camera's location and orientation is obtained through the calibration process. Calibration of cameras can be done at one processing center, which collects image feature points from all cameras in the system and based on that, it estimates the calibration parameters for the entire system. However, such a calibration method is expensive in terms of energy and is not scalable, and thus it is not suitable for energy-constrained visual sensor networks. Therefore, visual sensor networks require distributed energy-efficient algorithms for multi camera calibration.

The localization algorithms developed for wireless sensor networks cannot be used for calibration of the cameras since they do not provide sufficient precision, nor do they provide information on the camera orientation.

3. Autonomous Camera Collaboration

Visual sensor networks are envisioned as distributed and autonomous systems, where cameras collaborate and, based on exchanged information, reason autonomously about the captured event and decide how to proceed. Through collaboration, the cameras relate the events captured in the images, and they enhance their understanding of the environment. Similar to wireless sensor networks, visual sensor networks should be data-centric, where captured events are described by their names and attributes. Communication between cameras should be based on some uniform ontology for the description of the event and interpretation of the scene dynamics.

4. Time Synchronization

The information content of an image may become meaningless without proper information about the time at which this image was captured. Many processing tasks that involve multiple cameras (such as object localization) depend on highly synchronized cameras' snapshots. Time synchronization protocols developed for wireless sensor networks can be successfully used for synchronization of visual sensor networks as well.

5. Precise Location and Orientation Information

In visual sensor networks, most of the image processing algorithms require information about the locations of the camera nodes as well as information about the cameras' orientations. This information can be obtained through a camera calibration process, which retrieves information on the cameras' intrinsic and extrinsic parameters. Estimation of calibration parameters usually requires knowledge of a set of feature point correspondences among the images of the cameras. When this is not provided, the cameras can be calibrated up to a similarity transformation meaning that only relative coordinates and orientations of the cameras with respect to each other can be determined.

6. Local Processing

Local (on-board) processing of the image data reduces the total amount of data that needs to be communicated through the network. Local processing can involve simple image processing algorithms as well as more complex image/vision processing algorithms Thus, depending on the application, the camera nodes may provide different levels of intelligence, as determined by the complexity of the processing algorithms they use For example, low-level processing algorithms can provide a camera node with the basic information about the environment, and help it decide whether it is necessary to transmit the captured image or whether it should continue processing the image at a higher level. More complex vision algorithms enable cameras to reason about the captured phenomena, such as to provide basic classification of the captured object.

II. SYSTEM ANALYSIS

A. Existing System

In the Existing system,The existing system is the FrWF architecture. It is implemented on the Xilinx Artix-7 FPGA platform. It uses an input pixel width of 8 bits and a data-path width of 16 bits. The system stores the original image and its transformed coefficients in an external SD card. The system evaluates and compares the memory requirement and computational complexity of the FrWF architecture. Existing fixed-width AT designs employ direct or post-truncation methods. Proposed design compensates for truncation error using a bias estimation formula. Proposed design improves image reconstruction with higher PSNR for higher-texture images. Proposed design creates an advantage for optimizing other blocks in complex designs.

Disadvantges

1. Compression techniques in resource-constrained environments  lead to degradation  image quality.
2. Implementing complex compression on Resource contrained visual sensor nodes.
3. Balancing with trade-offs between  performance, complexity&energy efficiency requires careful design .
4. Aggressive compression techniques remove redundancy from the image data.

B. Proposed System

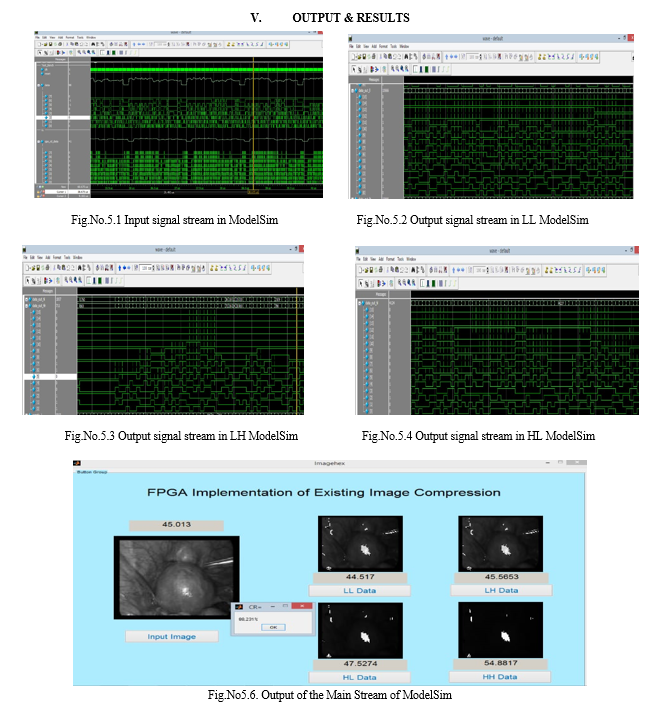
In a recent technology of digital image processing algorithm will have priority in all digital gadgets and all signal processing applications such image, video transmission and receptions in this case it will take large area and more power consumptions in VLSI methodology to transfer and retrieve the original images, therefore image compression technique of JPEG, DCT coding will take a more complications to compress images. Here in this proposed work will compress the image using discrete wavelet transform (DWT) with different level of image compression such as High-High, High-Low, Low-High, Low-Low methods and proved the performance with low area and low power consumptions. Finally this work will present in VLSI methodology of Verilog HDL and synthesized in Xilinx FPGA.

 ADVANTAGES:

1. Simplified Hardware: With fewer arithmetic operations involved, the hardware design can be simplified, requiring fewer processing elements such as multipliers and adders.     
2. Reduced Arithmetic Operations: The lifting scheme involves simpler arithmetic operations such as additions and subtractions, which typically consume less power compared to more complex operations like multiplications.
3. Energy-Efficient Data Transmission: In wireless visual sensor networks, where images are transmitted wirelessly, reducing the size of encoded images through efficient compression techniques results in lower energy consumption during data transmission.

III. SYSTEM ARCHITECTURE

A. Architecture Diagram

B. Architecture Specification

2D-DWT architecture explains the concept of extraction of images into low frequency and high frequency sub-bands.

The 2D-DWT architecture consists of forward DWT and inverse DWT in row and column wise on the input image’s header file.

In first stage the DWT is computed along the rows, in second stage DWT is computed along the column and hence achieving the first level of decomposition.

The XILINX coding is done in such a way that the whole code is reusable if the design is to be built in as a sub design for a larger design. The HAAR transform executes 2D-DWT and IDWT on images of pixel size 128x128 pixels.

We observe that the output image quality degrades substantially beyond 2nd-level of decomposition. In-fact 2-level decomposition is suf?cient to achieve the required compression ratio in most of the applications.

The data-?ow of proposed structure is identical to the parallel structure except the data-path width. The proposed structure has data-path width less by 3-bit compared to the parallel structure.

IV. LITERATURE SURVEY

Approximate hybrid multiplier design is proposed to reduce the data-path width of lifting 2-D discrete wavelet transform (DWT) especially for wireless visual sensor node applications. The ADP and EPI reduction is O(10ˆ2 ×). Compared with the existing parallel structure based on hybrid approximate radix-4 and radix-8 encoded Booth multiplier, the proposed approximate structure involves nearly 23% less ADP and 22% less EPI and calculates output images with nearly (4–7)-dB higher PSNR Inner-product computation forms the core of many important digital signal processing (DSP) functions such as linear and circular convolutions, correlation, digital filtering, and discrete trigonometric transforms. Many of these algorithms involve computation of inner product with a constant vector. Distributed arithmetic (DA) is widely used in such cases for efficient hardware realization of inner products Reference [1].

Parallel distributed arithmetic (PDA)-based structures are widely used for high-speed computation of inner product in digital signal processing (DSP) applications. To achieve higher bit saving with relatively less truncation error, we present here a novel approach using approximate look-up tables (LUTs), adder trees (ATs), and Wallace-like shift-AT (SAT) with truncated operands to obtain hardware-efficient fixed-width PDA-based inner-product structures. We find that the proposed inner-product structure-1 using approximate LUT (ALUT) and approximate AT offers nearly 20% higher bit saving, 20% saving in area-delay product (ADP) and offers relatively less truncation error than the existing structures. Proposed structure-3 offers nearly 60% higher bit saving and calculates outputs with almost the same or marginally less accuracy than the existing structures for higher coefficient word lengths Reference [2].

 An algorithm to compute the 2-D discrete wavelet transform (DWT) of high-resolution (HR) images on low-cost visual sensor and Internet of Things (IoT) nodes. The main advantages of the proposed segmented modified fractional wavelet filter (SMFrWF) are reduced computation (time) complexity and energy consumption compared to the state-of-the-art low-memory 2-D DWT computation methods. In particular, the conventional convolution-based DWT is very fast but requires large random access memory (RAM), as the entire image needs to be in the system memory. The fractional wavelet filter (FrWF) requires only a small RAM but has high complexity due to multiple readings of image lines. The proposed SMFrWF avoids the multiple readings of image lines, thus reducing the memory read access time and, thereby, the complexity Reference[3].

Conventionally, fixed-width adder-tree (AT) design is obtained from the full-width AT design by employing direct or post-truncation. In direct-truncation,and in the case of post-truncation   $p$   lower order-bits of final-stage adder output are truncated, where p=⌈log2N⌉ and  N  is the input-vector size. Both these methods does not truncated input. A bias estimation formula based on probabilistic approach is presented to compensate for the truncation error.

Conclusion

The approximation technique is used to reduce ON-chip memory of lifting 2-D DWT structures without any overhead. In the proposed scheme, data-path width of fixed-width lifting 2-D DWT is optimized for different decomposition levels. To further reduce the data-path width, a novel hybrid approximate multiplier design is proposed using radix-4 and radix-16 Booth encoding schemes. The proposed hybrid multiplier takes multiplier operand of size less by 3 bit and calculates full-width multiplier output with a marginal loss of accuracy, which is significant. A parallel approximate lifting 2-D DWT structure is derived using the proposed hybrid approximate multiplier with reduced data-path width. The proposed structure uses a data-path width of 9 and 11 for the first and second DWT levels and produces reconstructed images of 73 dB or higher PSNR. Compared with the existing FrWTbased 2-D DWT structures, the proposed structure involves a smaller data-path width and free from overhead. The proposed structure has nearly equal or marginally higher ON-chip memory requirement when compared with the existing FrWT-based 2-D DWT structures and involves a substantially less ADP and EPI. The reduction in ADP and EPI is O(102×). Besides, the proposed structure is free from memory-access overhead unlike the existing FrWT-based structures, which involves memory-access overhead O(Mb) per image. Therefore, the proposed approximate lifting 2-D DWT structure would be a better alternative to the existing FrWT-based structures for visual sensor node applications.

References

[1] Basant Kumar Mohanty\"Approximate Lifting 2-D DWT Hardware Design for Image Encoder of Wireless Visual sensors\", IEEE sensors journal, vol.23,no.7.1April 2023. [2] Basant Kumar Mohanty; Pramod Kumar Meher, \"An Efficient Parallel DA-Based Fixed – Width Design for Approximate Inner – Product Computation\", IEEE Access, vol. 6, pp. 20596-20608, 2022. [3] Mohd Tausif; Ekram Khan; Mohd Hasan; Martin Reisslein, \"SMRrWF: Segmented Modified Fractional Wavelet Filter: Fast Low-Memory Discrete Wavelet Transform (DWT)\", IEEE Access, vol. 5, pp. 5354-5365, 2021. [4] Y. Shu, C. Han, M. Lv and X. Liu, \"Fast super-resolution ultrasound imaging with compressed sensing reconstruction method and single plane wave transmission\", IEEE Access, vol. 6, pp. 39298-39306, 2018 [5] H. Zheng, K. Zeng, D. Guo, J. Ying, Y. Yang, X. Peng, et al., \"Multi-contrast brain MRI image super-resolution with gradient-guided edge enhancement\", IEEE Access, vol. 6, pp. 57856-57867, 2018. [6] G. Latif, D. N. F. A. Iskandar, J. M. Alghazo and N. Mohammad, \"Enhanced MR image classification using hybrid statistical and wavelets features\", IEEE Access, vol. 7, pp. 9634-9644, 2019. [7] S. A. Azzouzi, A. Vidal-Pantaleoni and H. A. Bentounes, \"Monitoring desertification in Biskra Algeria using Landsat 8 and Sentinel-1A images\", IEEE Access, vol. 6, pp. 30844-30854, 2018. [8] G. Chander and B. Markham, \"Revised Landsat-5 TM radiometric calibration procedures and postcalibration dynamic ranges\", IEEE Trans. Geosci. Remote Sens., vol. 41, no. 11, pp. 2674-2677, Nov. 2003. [9] S. Li and G. Jiang, \"Land surface temperature retrieval from Landsat-8 data with the generalized split-window algorithm\", IEEE Access, vol. 6, pp. 18149-18162, 2018. [10] S. C. Park, M. K. Park and M. G. Kang, \"Super-resolution image reconstruction: A technical overview\", IEEE Signal Process. Mag., vol. 20, no. 3, pp. 21-36, May 2003. [11] A. Madanayake, R. J. Cintra, V. Dimitrov, F. Bayer, K. A. Wahid, A. Edirisuriya, et al., \"Low-power VLSI architectures for DCT/DWT: Precision vs approximation for HD video biomedical and smart antenna applications\", IEEE Circuits Syst. Mag., vol. 15, no. 1, pp. 25-47, 1st Quart. 2015. [12] C. Chrysafis and A. Ortega, \"Line-based reduced memory wavelet image compression\", IEEE Trans. Image Process., vol. 9, no. 3, pp. 378-389, Mar. 2000.

Copyright

Copyright © 2024 K. Balaji, Arunkumar S, Dineshkumar L, Magesh A. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.