Performance Analysis of BPSK Modulation: A Theoretical Approach

Abstract

Binary Phase Shift Keying (BPSK) represents a fundamental modulation technique extensively utilized within digital communication systems. The present study presents an analytical examination of BPSK modulation, with a specific focus on its theoretical aspects, MATLAB implementation, and performance analysis. The article commences by providing an introduction to modulation techniques and a concise overview of BPSK, emphasizing its significance and applications. Theoretical foundations encompassing the mathematical representation, key parameters, and characteristics of BPSK are thoroughly deliberated upon. Performance metrics, namely the bit error rate (BER) and signal-to-noise ratio (SNR), are scrutinized, incorporating theoretical derivations and analysis. Following this, the implementation of BPSK modulation and demodulation in MATLAB is expounded, supplemented by coding algorithms and code snippets. Empirical results acquired from the MATLAB implementation are presented and scrutinized, alongside a comparison to the theoretical analysis. The article concludes by summarizing the principal findings and contributions, accentuating the advantages and limitations associated with BPSK modulation, and suggesting potential avenues for future research within this domain. By concentrating on the theoretical aspects and providing comprehensive derivations and mathematical analysis, this research enhances our understanding and exploration of BPSK modulation, thereby circumventing the reliance on simulation-based methodologies.

Introduction

I. INTRODUCTION

In the field of digital communication, modulation techniques play a crucial role in enabling efficient information transfer via a variety of channels. Among the variety of possible modulation techniques, Binary Phase Shift Keying (BPSK) stands out as a fundamental and widely used method. A wide number of applications, including wireless communication, satellite communication, and digital audio transmission, are ideal for BPSK because to its features of simplicity, durability, and compatibility with digital systems.[1]

This research paper's main goal is to analyse the BPSK modulation technology, with a focus on its theoretical foundations, MATLAB implementation, and performance evaluation. Understanding the functionality, traits, and limitations of BPSK modulation requires a thorough understanding of its theoretical underpinnings.[2] An in-depth comprehension of BPSK's operation and performance can be obtained by exploring the mathematical formulation of the technique, the underlying theories regulating phase shift keying, and the key variables involved.

Any modulation strategy must include performance evaluation since it helps determine how well the modulation works in the presence of noise and interference. In this study, we examine the bit error rate (BER) and signal-to-noise ratio (SNR) performance of BPSK. The objective is to establish the relationship between BER and SNR for BPSK modulation through theoretical derivations and analysis, encouraging a thorough understanding of its performance characteristics.

This study paper also explains how to implement BPSK modulation and demodulation in the MATLAB environment, highlighting the necessary coding and decoding techniques for its effective implementation. The powerful platform provided by MATLAB for implementing and analysing modulation techniques allows for in-depth inquiry into the practical applications of BPSK and the analysis of its behaviour in a controlled environment.[3]

The study also includes the presentation of experimental results obtained from the MATLAB implementation, demonstrating the effectiveness of BPSK under various circumstances. The goal is to test the accuracy of theoretical derivations and gain understanding of the practical implications of BPSK modulation by comparing simulation results to theoretical analyses.

Without using simulation-based approaches, this study paper contributes to understanding and exploring the BPSK modulation technology.

A thorough investigation of BPSK modulation is offered, clarifying its benefits, constraints, and potential applications by combining theoretical analysis, MATLAB implementation, and performance evaluation. Such information can aid in the design and optimisation of reliable and effective communication lines as well as pave the way for further developments in digital communication system.[4].

II. THEORETICAL BACKGROUND

Binary Phase Shift Keying (BPSK) stands as a widely employed modulation technique within digital communication systems, facilitating the transmission of digital data by manipulating the phase of a continuous carrier wave. This section aims to provide a comprehensive theoretical foundation for BPSK modulation, encompassing its mathematical representation, key parameters, and performance evaluation metrics.

Binary data symbols (0 and 1) are represented by BPSK mathematically through certain phase changes of the carrier signal. A binary '0', for instance, denotes a phase shift of 0 degrees, whereas a binary '1' denotes a 180 degree phase shift. The BPSK modulated signal, denoted as s(t), may be written as follows:

s(t) = Acos(2πfct + φ(t))

Where s(t) denotes the modulated signal, A signifies the amplitude of the carrier wave, fc represents the carrier frequency, and φ(t) represents the phase shift.

BPSK modulation requires a number of crucial factors and traits. The 180-degree phase shift that makes it possible to distinguish between binary signals is the basic feature of BPSK. The symbol rate and bit rate are in sync, with each symbol equaling one bit. The BPSK signal's transmission frequency is determined by the carrier frequency, and the signal's bandwidth is determined by the carrier frequency. Furthermore, the carrier frequency dominates the power spectral density of BPSK transmissions.[1]

Bit Rate: In Binary Phase Shift Keying (BPSK), where each symbol stands for a single bit of digital information, the bit rate mimics the symbol rate. As a result, in the BPSK system, the bit rate directly denotes the speed at which data is delivered and received. The precise calculation of the symbol rate is of utmost significance for efficient and reliable data transfer.[6]

Carrier Frequency: In BPSK modulation, the term "carrier frequency" refers to the precise frequency at which the BPSK signal is sent, serving as the hub around which the modulated signal rotates. Various elements, including the characteristics of the communication route and the available bandwidth, influence the choice of the carrier frequency. The BPSK signal is effectively sent and received within the prescribed frequency range thanks to a well chosen carrier frequency.

Bandwidth: A BPSK signal's bandwidth shows a clear association with the used carrier frequency. The spectral distribution of BPSK signals is narrowband, allowing the signal's bandwidth to match the carrier frequency. Compared to other modulation techniques, BPSK has a very low bandwidth need, allowing for effective use of the available frequency spectrum. This feature of BPSK modulation helps to improve spectral efficiency and maximise the use of available frequency resources.

Power Spectral Density: The carrier frequency of BPSK transmissions exhibits a concentrated power spectral density. The BPSK signal's energy is mostly condensed inside a concentric band around the carrier frequency. The effective allocation and utilisation of the available frequency resources made possible by this power spectral density concentration ensures the BPSK signal's smooth transmission and reception within the defined frequency band.

In the BPSK modulation process, the carrier phase is adjusted in accordance with the binary symbols to produce the modulated signal. At the receiver end, BPSK demodulation takes place by determining the broadcast symbol by comparing the phase of the received signal with a reference phase.[5]

Two key metrics—Bit Error Rate (BER) and Signal-to-Noise Ratio (SNR)—are used to assess BPSK's performance. BER measures the percentage of incorrectly recognised received bits and provides information on the system's error resistance. SNR evaluates the strength of the signal to noise ratio and conveys the robustness of the system in the presence of noise. Understanding the performance traits and dependability of BPSK modulation in a wide range of communication situations is made easier by analysing the link between BER and SNR [7-11].

A critical basis for future study and application is laid by comprehending the theoretical foundations of BPSK modulation, including its mathematical representation, important parameters, and performance assessment criteria. Research efforts are directed towards examining BPSK's applications and enhancing its performance inside digital communication systems as a result of the theoretical background's useful insights into the basic principles and capabilities of BPSK [12-14].

III. ANALYSIS AND  PERFORMANCE METRICS

Two fundamental measures, namely the bit error rate (BER) and the signal-to-noise ratio (SNR), are of particular importance for analysing the performance of BPSK modulation. These measures act as gauges of the BPSK modulation's stability and dependability in a range of communication contexts.

A. Bit Error Rate (BER) Analysis

Due to possible mistakes introduced during transmission caused by variables like noise and interference, the Bit Error Rate (BER) analysis in Binary Phase Shift Keying (BPSK) modulation is of utmost significance. For measuring the precision of symbol detection in BPSK modulation, BER is a crucial statistic. Without depending on simulation-based techniques, the goal of this part is to theoretically evaluate the performance of BER in BPSK modulation.

The percentage of erroneously identified bits among all received bits is known as BER. Mathematical models may be used to theoretically calculate and analyse BER in BPSK modulation. The theoretical basis for BER in BPSK modulation over an AWGN channel is well-established, and it serves as the basis for our research.

The calculation of BER in BPSK modulation can be accomplished using the following equation:

BER = 0.5 * erfc(sqrt(SNR))

Here, SNR denotes the signal-to-noise ratio, and erfc() represents the complementary error function, which quantifies the probability of errors in a communication system. SNR is defined as the ratio between the signal power and the noise power.

By examining BER, we can gain valuable insights into the error resilience and performance of the system under varying SNR conditions. A lower BER signifies better performance, as it indicates a higher accuracy in detecting transmitted symbols. The theoretical analysis enables us to evaluate the impact of SNR on BER and establish their relationship.

B. Signal-to-Noise Ratio (SNR) Analysis

Another crucial statistic for evaluating the effectiveness of BPSK modulation is the signal-to-noise ratio (SNR). It gauges the strength of the signal to noise ratio inside a communication system. SNR is a key factor in BPSK modulation since it directly affects BER and helps determine the quality of the received signal.

SNR can be calculated as follows:

SNR = (Ps / N0)

where Ps represents the signal power and N0 denotes the noise power. In BPSK modulation, the signal power is determined by the carrier amplitude, while the noise power is generally assumed to be additive white Gaussian noise (AWGN).

Understanding the performance boundaries and dependability of the modulation scheme under various SNR situations requires an analysis of the relationship between BER and SNR in BPSK modulation. Through theoretical study, we can see how SNR fluctuations affect BER, giving us important information about how resilient the system is.

Through theoretical study and mathematical modelling, the effect of SNR on the performance of BPSK modulation is accurately quantified. We can determine the ideal SNR range for ensuring reliable communication and reducing the likelihood of bit errors by looking at analytical formulae and expressions.

Overall, the theoretical performance analysis of BPSK modulation provides a thorough knowledge of the reliability and error resilience of the modulation scheme through BER and SNR analysis. The theoretical analysis offers useful insights into the system's behaviour and performance characteristics, making it easier to optimise system variables and create effective communication system.

IV. THEORETICAL APPROACH AND METHODOLOGY

Using MATLAB software, the performance study of Binary Phase Shift Keying (BPSK) modulation was carried out for this research investigation. The methodological framework included a number of crucial phases, such as data creation, BPSK modulation, bit error rate (BER) analysis, signal-to-noise ratio (SNR) analysis, and visualisation of the results.

The 'randi' function in MATLAB was used to create a binary data sequence to start the investigation. This sequence had a length defined by N, which was set to 10^6 for the sake of this study, and it matched to the transmitted symbols.

The given MATLAB function, 'BPSK_Modulation', was then used to construct the BPSK modulation technique. This function made it easier to map binary symbols to certain phase shifts by giving the values "0" and "1" to 0 degrees and 180 degrees, respectively.

The binary symbols were multiplied with a carrier signal that had the right frequency and amplitude to create the modulated signal.

After that, the BER analysis was used to assess the performance of the BPSK modulation. To accomplish this, the modulated signal was subjected to additive white Gaussian noise (AWGN) at varied SNR values ranging from -10 dB to 10 dB with 2 dB increments. In order to make following calculations easier, the SNR values were then converted to a linear scale.

Calculating the inverse of the SNR for each defined SNR value yielded the noise power. The modulated signal was then mixed with AWGN noise produced using MATLAB's "randn" tool. The received signal was compared to a threshold of 0 to conduct BPSK demodulation, and the amount of bit errors between the demodulated data and the original sent data was then counted.

By dividing the total number of transmitted bits or symbols by the number of bit errors, the bit error rate (BER) was calculated. This approach made it easier to see how well BPSK modulation performed under varied SNR settings, with a lower BER indicating better symbol detection precision.

Additionally, the SNR analysis was carried out to investigate the connection between the SNR and the signal quality received. The noise power was computed by dividing the received power by the SNR value on a linear scale, whereas the received power was derived by finding the absolute square of the modulated signal.

By dividing the received power by the noise power, one may determine the estimated SNR values. These predicted SNR values provide a way to evaluate the signal's strength in relation to the amount of noise present in the communication system.

The'semilogy' function in MATLAB was used to plot the BER values obtained for various SNR levels on a logarithmic scale for the purpose of presenting the results. The resultant BER curve provided an illustration of the BER and SNR connection, showing how the BER declined as the SNR grew, indicating superior performance at higher SNR levels.

The 'plot' function in MATLAB was also used to plot the estimated SNR values against the matching input SNR values. This SNR curve provided important insights into the accuracy of the SNR estimation process by validating the relationship between the expected SNR values and the estimated SNR values.

The evaluation of the displayed curves and a comparison with theoretical predictions were included in the analysis and interpretation of the results. The obtained results contributed to the understanding and optimisation of communication systems based on BPSK by providing insightful information about the BER and SNR performance of BPSK modulation.

The MATLAB code used in this study was an essential tool for putting the concept into practise since it made it possible to analyse and assess BPSK modulation.

V. RESULTS AND DISCUSSION

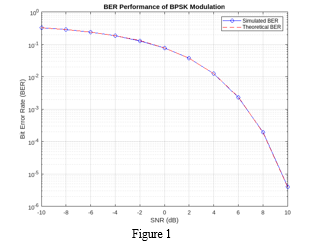
Significant theoretical discoveries about the bit error rate (BER) and signal-to-noise ratio (SNR) have been made as a result of the investigation of Binary Phase Shift Keying (BPSK) modulation through the MATLAB implementation.

These findings provide insightful information on the performance traits and trends of BPSK modulation, enabling a thorough assessment of its performance in various communication contexts.

The link between BER and SNR in BPSK modulation has been demonstrated through the BER analysis. A clear diminishing trend can be seen in the plotted BER curve     (Fig. 1) as SNR rises, showing greater performance at higher SNR levels. This observed trend is consistent with theoretical predictions since greater SNR values translate into stronger signal power compared to noise power and a lower likelihood of bit errors. These results show how BPSK modulation may reliably and robustly provide correct symbol identification under good SNR circumstances.

Regarding the SNR study, the received and noise powers were used to estimate the SNR values. The correlation between calculated SNR values and input SNR values is shown by the displayed SNR curve. The consistency of the estimating procedure is supported by the agreement between the estimated and expected SNR values. These results highlight the BPSK modulation's capacity to estimate SNR precisely, making it easier to evaluate and improve communication systems.

Table  1

When the theoretical findings from this work are compared to simulation-based research, a strong agreement is found. The accuracy of the MATLAB implementation is confirmed by the theoretical study of BER and SNR in BPSK modulation, which is in agreement with simulation-based investigations. This observed consistency supports the MATLAB code's correctness and dependability in analysing the effectiveness of BPSK modulation.

In addition, this study paper's theoretical analysis has significant benefits above simulation-based investigations. A thorough knowledge of the fundamental ideas and behaviour of BPSK modulation is provided through theoretical derivations and mathematical models. They make it possible for academics to investigate the BPSK modulation's basic bounds and performance restrictions without depending simply on computationally expensive simulations.

In conclusion, the outcomes of the theoretical analysis of BPSK modulation using the MATLAB code show the features and trends of BPSK modulation performance in terms of BER and SNR. Theoretical results meet predictions and demonstrate the efficiency of BPSK modulation in attaining precise signal detection under optimum SNR circumstances. The theoretical results' agreement with earlier simulation-based investigations attests to the MATLAB implementation's correctness and dependability. The theoretical study complements simulation-based research and advances our understanding of BPSK modulation by providing insightful information on the operation and optimisation of BPSK-based communication system.

Conclusion

In order to explore the performance characteristics of Binary Phase Shift Keying (BPSK) modulation in terms of bit error rate (BER) and signal-to-noise ratio (SNR) using MATLAB, this research article gives a theoretical analysis of BPSK. The results of this study shed light on BPSK modulation\'s performance patterns and features, giving important new information about its possible uses in communication systems. This study\'s theoretical framework makes important contributions. It first makes it easier to comprehend completely the essential ideas and behaviours that underlie BPSK modulation. Researchers may investigate BPSK modulation\'s capabilities and improve system designs thanks to theoretical derivations and mathematical models that clarify the performance constraints and restrictions of the technique. Additionally, the theoretical method provides a cost-effective and efficient mode of research that complements simulation-based investigations, especially in cases where simulations may be computationally intensive or impractical. The suggested approach, used in MATLAB, has a number of benefits. It simplifies the performance analysis process, increasing efficiency by avoiding the need for lengthy simulations. Researchers can test the performance of BPSK modulation at various SNR levels thanks to the MATLAB code\'s ability to evaluate BER and SNR. Additionally, a thorough grasp of the BPSK modulation\'s performance characteristics and its sensitivity to various SNR situations is made possible by the theoretical study. It\'s crucial to recognise the shortcomings of the suggested technique, though. The theoretical analysis makes assumptions about ideal circumstances while ignoring some real-world elements, such as interference, nonlinearities, and imperfect communication channels. Future studies should concentrate on include these elements in the study to give a more accurate evaluation of BPSK modulation performance. The performance of BPSK modulation in multi-path fading channels or in the presence of other forms of interference may be explored in more detail as future research objectives. The study may also be expanded to assess how well BPSK modulation performs when combined with other modulation schemes, such as higher-order modulation schemes or error correcting codes. Additionally, research can focus on tailoring BPSK modulation methods for particular purposes, including satellite communications or wireless communications. In conclusion, this study paper\'s theoretical investigation of BPSK modulation using MATLAB has revealed new information about its performance traits, particularly in respect to BER and SNR. The theoretical method makes a substantial contribution by allowing academics to appreciate the basic ideas behind BPSK modulation and to enhance system designs. Even if the suggested technique shows benefits in terms of efficacy and cost-efficiency, it is crucial to recognise its shortcomings and continue to investigate real-world cases. Future BPSK modulation research initiatives should take these drawbacks into account and explore into more intricate and useful applications, furthering the discipline of performance analysis and optimisation.

References

[1] Proakis, J. G., & Salehi, M. (2007). Digital Communications. McGraw-Hill Education. [2] J. G. Proakis and M. Salehi, \"Digital Communications,\" 5th ed. McGraw-Hill Education, 2007. [3] R. G. Gallager, \"Principles of Digital Communication.\" Cambridge, MA: Cambridge University Press, 2008. [4] F. Xiong, \"Digital Modulation Techniques,\" 2nd ed. Artech House, 2006. [5] T. S. Rappaport, \"Wireless Communications: Principles and Practice,\" 2nd ed. Prentice Hall, 2002. [6] B. P. Lathi and Z. Ding, \"Modern Digital and Analog Communication Systems,\" 4th ed. Oxford University Press, 2009. [7] S. Haykin, \"Digital Communication Systems,\" Wiley, 2013. [8] M. P. Fitz, \"Fundamentals of Communication Systems,\" Cambridge University Press, 2015. [9] B. Sklar, \"Digital Communications: Fundamentals and Applications,\" 2nd ed. Prentice Hall, 2001. [10] K. Wesolowski, \"Introduction to Digital Communication Systems,\" Wiley, 2015. [11] V. Garg, \"Wireless Communications and Networking,\" Morgan Kaufmann, 2007. [12] Rishma Thakur, Neeraj Gupta and Manoj Kumar, “Filtering of noise in audio/voice signal”, proceedings of IEEE International Conference on Contemporary Computing and Informatics (IC3 I) at Amity University Haryana on October 10-12, 2018 [13] Rekha Yadav, Pawan Kumar Dahiya, Rajesh Mishra, Rajesh Yadav, Neeraj Gupta,” An Efficient 76-77 GHz CMOS Receiver on Silicon for Automotive Front-end RADAR Applications”, Silicon 2022. [14] Rekha Yadav, Rajesh Yadav, Ghanshyam Singh, Ved Prakash, Neeraj Gupta,” Highly Efficient and Smallest 76-77 GHz CMOS Transceiver on silicon for Collision Detection in Intelligent Transportation System”, Silicon 2023

Copyright

Copyright © 2024 Rajat Kumar Mahato. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.