Ijraset Journal For Research in Applied Science and Engineering Technology

Abstract

Due to its decentralised structure, blockchain technology has acquired great traction in fields such as banking, business, healthcare, and e-voting due to its decentralised nature. Because of the difficulty of lesser throughput, many blockchain systems have sought efficiency enhancements. Mathematical models such as Markov processes, queuing theory, and game theory are employed to analyze various aspects of blockchain systems, including mining processes, consensus mechanisms, and overall performance. This paper focuses on using M/M/1 queuing theory to analyze blockchain mining processes, utilizing the Raft algorithm for consensus. A simulation done by using python is also provided.

Introduction

I. INTRODUCTION

The successful launch of Bitcoin in 2010 brought blockchain into the spotlight. Numerous companies are adopting blockchain technology including software, financial services, healthcare, and banking. Blockchain is a peer-to-peer distributed database and transaction system that is decentralized, secure, and openly accessible. Its security and performance are largely dependent on consensus algorithm. Consensus algorithms are essential for maintaining the performance and security of blockchain networks. Practical Byzantine Fault Tolerance (PBFT) and Raft are the traditional consensus algorithms used in private blockchain.

Raft algorithm has been widely used in distributed systems because of its high efficiency and simplicity as compared with PBFT. It utilizes a leader-based consensus process, where the leader manages client requests, duplicates logs, and distributes them to nodes. It allows freshly created blocks to be directly added to the chain without additional consensus procedures. However, Raft can tolerate up to 50% of crash fault nodes but cannot handle malicious nodes. Certified nodes act as participants in private blockchain networks, ensuring the integrity and security of the system.

The factors that influence blockchain performance are.

1. Transaction Latency: Transaction latency refers to the time between the time a transaction is requested and finally committed. Transaction latency must be short for a blockchain to achieve high performance.
2. Transaction Throughput: Transaction throughput represents the rate at which a valid transaction is processed within a set period of time and is referred to as TPS.

II. LITERATURE REVIEW

Memon et. al. [5] (2019) analyzed a model based on queuing theory that replicated a blockchain. The M/M/1 queue was used for the mining pool, while the M/M/c queue was used as the memory pool, in the provided model. This model was a straightforward but efficient method to show a variety of significant measurements, including (a) The number of client requests per block (b) The mining time of each block (c) System Throughput (d) Memory-pool count (e) Waiting Time in memory-pool (f) The number of unconfirmed client requests in the whole System (g) Total number of client requests and (h) number of blocks generated.

Kim et. al. [3] (2021) proposed a mechanism for electing leaders via the Raft algorithm considering network stability. Developed method reduced the probability of network split using Raft. It also prevented further performance degradation when a blockchain node network is unstable.

Tomi? [7] (2021) studied functional advantages and disadvantages of observed protocol. Characteristics compared: security, trust among participants, throughput, and scalability. They concluded that no protocol showed complete dominance in all aspects of the comparison. Most protocols in practice show deviations from the theoretically stated optimal results. All the observed proto - cols like PBFT, FBA, DBFT were intended for permissioned blockchains, not all have the same purpose. So, when choosing a consensus protocol for blockchain applications, take into purpose priority.

Vora and Gor [8] (2022) used blockchain queueing theory to analyze theoretical transaction-confirmation time of a block. The blockchain system was examined at arrival as well as departure point. This paper reflects on M/G/1 queue and examines the blockchain system using queueing theory.

Yang [10] (2022) performed a deep analysis of the consensus techniques for running BaaS in clouds. Experimented with variations on the number of orderer nodes, batch sizes, payload sizes, and fault nodes. Based on the experiment results, they provide key findings on 1) resource consumption of the three consensus algorithms, 2) the effect of block size and block creation rate on performance, and 3) the existence of high and low orderer nodes in terms of CPU cycles. That study contributed to understanding the characteristics of resource consumption.

Vora and Gor [9] (2022) provided a markovian queueing model of the form Mb/M/1 as the theoretical foundation for creating a Proof of Authority (PoA)-based blockchain system. It was focused on the stochastic behavior of the client requests, consensus process, and throughput. Client requests were thought to arrive in batches with a Poisson distribution, according to the model. The queueing model had been used to analyze the PoA consensus protocol. To demonstrate the reliability of the underlying simulation model, numerical experiments carried out in Python were presented. It had been noted that the block's optimal throughput rate was attained for small numbers of client requests.

III. RAFT CONSENSUS ALGORITHM [2],[3]

Consensus means multiple servers agreeing on the same information. The Raft consensus algorithm is a distributed consensus algorithm that verifies that few nodes in a distributed system agree on a system's condition.

It is used in permissioned blockchain. In permissioned blockchain participants must have an invitation or permission to participate. Raft consensus algorithm was introduced in 2014 by Diego Ongaro and John Ousterhout after Reliable, Replicated, Redundant and Fault-Tolerant.

1. Leader Election: In Raft, there is always one leader that coordinates the actions of the nodes in the cluster. The first step is to elect a leader. The nodes in the cluster send out "heartbeat" messages to each other. If a node does not receive a heartbeat message from the leader for a certain period, it will start an election. Each node will send out a vote request message to all other nodes in the cluster, and the node with the most votes become the leader.
2. Log Replication: Once a leader is elected, it begins to accept requests from clients and sends Append Entries messages to the other nodes in the cluster to replicate its log entries. Each log entry contains a command from the client and a unique index. The leader waits for acknowledgements from most nodes before it can commit the log entry.
3. Commitment: Once a leader receives acknowledgments from most nodes, it commits the log entry to its own log and sends out a Commit message to all other nodes in the cluster. Upon receiving the Commit message, each node applies the log entry to its state machine, which updates the state of the system.
4. Recovery: If the leader fails or loses connectivity, a new leader election is started. In this case, the new leader will search for the most up-to-date log entry and replicate it to all nodes that have outdated logs.

A. Election Process

In the Raft consensus algorithm, the nodes (i.e., server computers) vote for a leader, and the other nodes then follow the leader. Considering that every node is trustworthy and does not have any malicious intentions. When a timeout occurs, the system elects a new leader because there is no one now. During the election process few candidates compete for the role of leader and the rest of the nodes choose the winner.

Each node has a consensus module, which is always operating within one of the following modes:

1. Follower: A passive node, which only responds to RPC’s and will not initiate any        communications.   
2. Candidate: An active node which is attempting to become a leader, they initiate Request Vote RPC’s.
3. Leader: An active node which is currently leading the cluster, this node handles requests from clients to interact with the replicated state machine and initiates Append Entries RPC’s.
4. Voting Request: The candidate who receives the most votes become the leader. The followers can vote in support of or against the leader's proposition. The leader candidate requests the votes. This voting request contains two parameters:
5. Term: The last calculated number known to candidate + 1.
6. Index: Committed transactions available to the candidate.

These methods perform in numerous rounds, and the term indicates a new voting cycle. If the last round of voting is completed, the next term will be the old term number Plus 1. The index displays the committed transactions that are candidates but not yet committed.

B. Making Decisions as a Follower Node

After receiving a voting request, the nodes' responsibility is to give their vote for or against the candidate. So, in the Raft consensus approach, a leader is chosen in this manner. Each node compares the term and index that it has received to the corresponding, currently known values. The voting request is received by the node. It compares the previously viewed term to the newly received term. Because the node views this request as an old request, if a newly received term is less than the already observed term, it discards it. The newly received term is greater than the previously seen term. It compares the recently obtained index number to the one that has already been observed. It votes for the candidate if the recently obtained index number is higher than the one already observed; else, it stays away.

C. Leader Ordered Node Selection [10]

The candidates that receive the majority of the nodes' votes are declared the leaders, while the remaining nodes are made up of their followers. Through a "heartbeat mechanism," Raft maintains at least one leader node. The leader node sends "heartbeats" on a regular basis to alert the following ordered nodes about its presence. The leader election is started by the follower ordered nodes if they do not get the heartbeat by a specific time. When a new leader ordered node is elected, it begins sending heartbeats to the follower ordered nodes and generating blocks.

IV. MATHEMATICAL MODEL

This section describes the mathematical queuing approach of raft consensus algorithm. It determines the client request arrival, leader election process and block building process in blockchain. Here, M/M/1 queueing model is considered for this raft consensus system, in which arrivals are modelled as a Poisson process and service times are exponentially distributed. Client request arrives in the system at rate λ .  1/μ  is the required service time taken by the leader node as a server. Here, the election timeout is not considered.                 

1. Arrival Process:  The client requests are arrived at rate λ  in the network of nodes. The client requests are accumulated in the FCFS[7] fashion.
2. Service Process: When client requests come into the system, it is first checked whether there is a leader or not. If there is no leader, then the leader’s election is processed, and the leader is elected. The new leader sends a heartbeat message to all follower nodes.

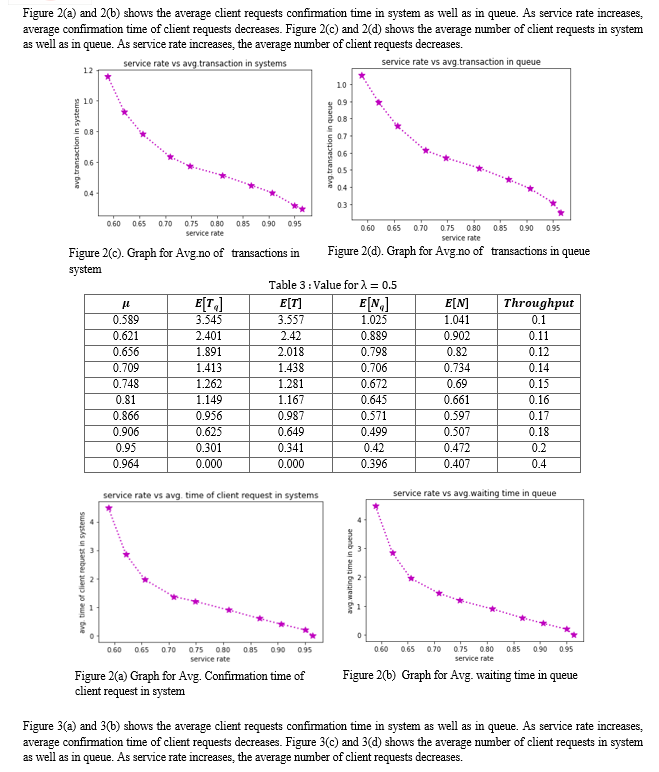
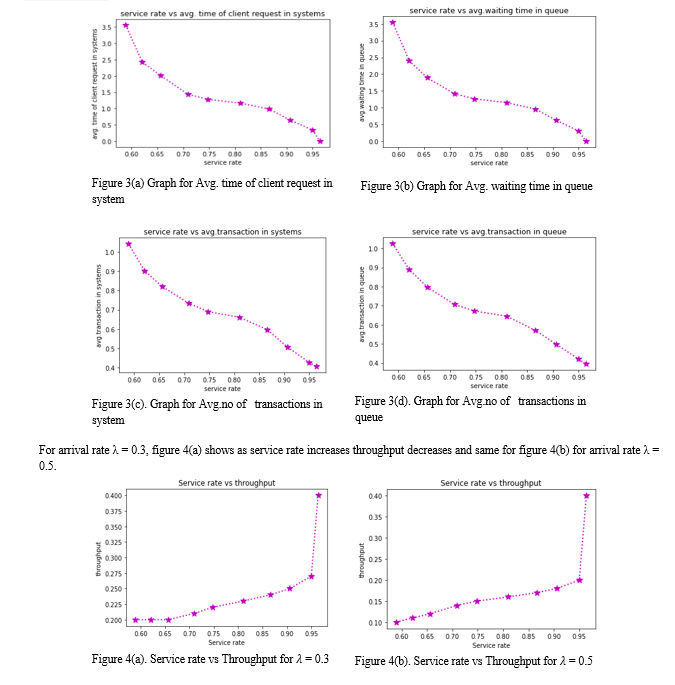
Conclusion

This study presents a theoretical examination of the Raft consensus process using M/M/1 queuing model for blockchain. The proposed methodology is straightforward yet effective to display numerous different parameters, such as average number of client request, average waiting time in the system as well as in queue. The analysed results demonstrates that as the service rate increases, throughput increases, and the other primary performance measures decreases. Numerical experiments and results are performed in python. This study opens several future research directions for optimizing the performance of the Raft consensus algorithm, considering scalability, network characteristics, empirical validation, comparative analysis with other algorithms, and exploring different workload scenarios. These approaches can contribute to the development of efficient and robust consensus algorithms for blockchain systems.

References

[1] Baliga, A., Subhod, I., Kamat, P., & Chatterjee, S. (2018). “Performance evaluation of the quorum blockchain platform”. arXiv preprint arXiv:1809.03421. [2] Huang, D., Ma, X., & Zhang, S. (2019). “Performance analysis of the raft consensus algorithm for private blockchains”. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 50(1), 172-181. [3] Kim, D., Doh, I., & Chae, K. (2021, January). “Improved raft algorithm exploiting federated learning for private blockchain performance enhancement”. In 2021 International Conference on Information Networking (ICOIN) (pp. 828-832). IEEE. [4] Li, Q. L., Ma, J. Y., & Chang, Y. X. (2018). “Blockchain queue theory”. In Computational Data and Social Networks: 7th International Conference, CSoNet 2018, Shanghai, China, December 18–20, 2018, Proceedings 7 (pp. 25-40). Springer International Publishing. [5] Memon, R.A.; Li, J.P.; Ahmed, J. “Simulation Model for Blockchain Systems Using Queuing Theory”. Electronics 2019, 8, 234. https://doi.org/10.3390/electronics802023004 [6] Ongaro, D., & Ousterhout, J. (2014). “In search of an understandable consensus algorithm”. In 2014 {USENIX} Annual Technical Conference ({USENIX}{ATC} 14) (pp. 305-319). [7] Tomi?, N. Z. (2021). “A review of consensus protocols in permissioned blockchains”. Journal of Computer Science Research, 3(2), 32-39. [8] Vora S.& Gor R. (2022), “Study of Average Transaction Confirmation time in a Blockchain using Queueing Model”, IOSR Journal of Computer Engineering (IOSR-JCE),24(3), 2022, pp. 60-68. [9] Vora and Gor, “Queueing Model for PoA based Blockchain system” IOSR Journal of Mathematics (IOSR-JM). [10] Yang, G., Lee, K., Lee, K., Yoo, Y., Lee, H., & Yoo, C. (2022). “Resource Analysis of Blockchain Consensus Algorithms in Hyperledger Fabric”. IEEE Access, 10, 74902-74920.

Copyright

Copyright © 2023 Stuti Vora, Nidhi Thakkar, Ravi Gor. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.