Quantum Computing

Abstract

The revolutionary technology known as quantum computing has the potential to completely transform several industries, including material research, medicine development, optimization, and cryptography. Quantum computers use the ideas of quantum mechanics to harness the power of quantum bits, or qubits, in contrast to classical computers, which function using binary digits, or bits. These qubits, which exist in a superposition of states, allow quantum computers to operate at a computational rate never before possible, potentially tackling challenging issues that are beyond the capabilities of classical systems.

Introduction

I. INTRODUCTION

Quantum computing is a rapidly developing field of study that explores the principles of quantum mechanics to design and build computers capable of solving complex problems more efficiently than classical computers. While classical computers use bits as the fundamental unit of information, which can represent either a 0 or a 1, quantum computers use quantum bits or qubits, which can exist in multiple states simultaneously, thanks to a property called superposition. Superposition is one of the fundamental concepts in quantum computing, allowing qubits to be in a combination of 0 and 1 at the same time. This characteristic enables quantum computers to perform parallel computations and consider multiple possibilities simultaneously, significantly enhancing their computational power. Another key principle in quantum computing is entanglement. When qubits become entangled, the state of one qubit becomes intrinsically linked to the state of another, regardless of the physical distance between them. This property enables quantum computers to process information in a highly interconnected manner, potentially leading to exponential speedups for certain types of calculations. The power of quantum computing lies in its ability to leverage superposition and entanglement to perform computations on a scale that surpasses classical computers for specific types of problems. Quantum computers have the potential to solve complex mathematical and optimization problems, simulate quantum systems, break certain encryption algorithms, and contribute to advancements in fields like drug discovery, materials science, and artificial intelligence. However, building a practical and large-scale quantum computer is still a significant technological challenge. Quantum systems are highly delicate and prone to errors due to environmental interference, a phenomenon known as quantum decoherence. Researchers are actively working on developing error-correcting techniques and qubit designs to mitigate these challenges and create stable quantum computers capable of performing meaningful computations. In recent years, there has been substantial progress in the development of quantum hardware, algorithms, and quantum programming languages, as well as increased interest from academia, industry, and government organizations. While quantum computers are still in the early stages of development, they hold tremendous potential to revolutionize various fields and tackle complex problems that are currently intractable for classical computers. Quantum computing and classical computing are two distinct paradigms of computation with fundamental differences in terms of how information is processed and stored. Here are the key differences between quantum computing and classical computers:

A. Basis of Computation

Classical computers, which include most of the devices we use today, rely on bits as the basic unit of information. A bit can represent a value of either 0 or 1. On the other hand, quantum computers use quantum bits, or qubits, which can represent a superposition of 0 and 1 simultaneously. This ability to exist in multiple states simultaneously is one of the key features of quantum computing.

B. Processing Power

Quantum computers have the potential to solve certain problems much more efficiently than classical computers. They leverage quantum phenomena like superposition and entanglement to perform computations in parallel across all possible states of the qubits. This parallelism allows quantum computers to solve certain types of problems exponentially faster than classical computers, particularly in areas such as prime factorization, optimization, and simulation of quantum systems.

C. Computational Models

Classical computers follow the principles of classical physics and use algorithms based on classical logic and mathematics, such as Boolean logic and Turing machines. Quantum computers, on the other hand, operate on principles of quantum mechanics. They utilize quantum algorithms, such as Shor's algorithm for factoring large numbers or Grover's algorithm for searching an unsorted database, which exploit the unique properties of qubits to achieve computational speedups.

D. Error Correction

Error correction techniques are employed by classical computers to guarantee the precision and dependability of their calculations. Due to quantum decoherence and noise, sustaining the delicate quantum states of qubits is a major difficulty for quantum computers. To solve these problems and maintain the integrity of quantum information, quantum computing thus needs advanced error correction and fault-tolerant algorithms.

E. Applications

Classical computers are well-suited for a wide range of everyday computing tasks, such as web browsing, data processing, and software applications. Quantum computers, while still in their early stages of development, hold promise for solving complex problems in various fields, including cryptography, optimization, drug discovery, material science, and quantum simulations.

II. APPLICATION AREAS

Quantum computing could have an impact on many different industries and solve difficult issues that traditional computers find difficult. These are a few areas of application where quantum computing may have a big impact.

A. Security and Cryptography

Quantum computers have the potential to break many of the currently used cryptographic algorithms, such as RSA and elliptic curve cryptography, which rely on the difficulty of factoring large numbers. Quantum-resistant cryptography algorithms are being developed to withstand attacks from quantum computers.

B. Optimization and Logistics

Complex system optimization and increased productivity in domains like supply chain management, transportation, scheduling, and route optimization can be achieved with the aid of quantum computing. It can solve optimization problems more quickly and accurately, which helps reduce costs and improve resource usage.

C. Drug Discovery and Material Science

Quantum computers can simulate the behavior and properties of molecules and materials with high precision. This capability can accelerate the discovery of new drugs, catalysts, and materials by accurately modeling their interactions, properties, and behavior, thus speeding up the development process.

D. Machine Learning and Artificial Intelligence

Because quantum computing allows for the faster processing of massive datasets and the execution of intricate optimizations, it can improve machine learning algorithms. Artificial intelligence may advance because of the potential for quantum machine learning algorithms to enhance pattern recognition, data analysis, and optimization tasks.

E. Financial Modeling

Complex financial modeling tasks including risk assessment, portfolio optimization, option pricing, and fraud detection can benefit from the use of quantum computing. These issues can be solved more quickly and precisely by quantum algorithms, which will enhance financial decision-making.

F. Energy and Environment

Quantum computing can contribute to solving energy-related problems, such as developing more efficient solar panels, optimizing energy distribution systems, and simulating complex chemical reactions for green energy generation. It can also help in environmental modeling, climate prediction, and finding solutions for climate change-related challenges.

G. Quantum Simulation

Quantum computers excel at simulating quantum systems, allowing researchers to better understand and explore the behavior of molecules, atoms, and other quantum phenomena. This capability can lead to advancements in quantum chemistry, quantum physics, and the development of new materials.

III. METHODOLOGIES

The methodology of quantum computing involves several key components and steps that are essential for designing and executing quantum algorithms. Here is a general outline of the methodology

A. Qubit Representation

Qubits are the fundamental units of information used in quantum computing. Qubits are commonly represented as a linear combination of 0 and 1, however they can exist in a superposition of states. Qubits can be realized in a variety of physical systems, including the energy levels of an atom, the spin of an electron, and the polarization of a photon. Challenge. 

B. Quantum Gate

Quantum gates are analogous to classical logic gates but operate on qubits. Quantum gates manipulate the state of qubits by performing unitary transformations. These gates include operations such as the Pauli-X gate (bit-flip), Pauli-Y gate (bit- and phase-flip), Pauli-Z gate (phase-flip), Hadamard gate (superposition creation), and others. Gate operations allow for the manipulation and transformation of qubit states to perform computations.

C. Quantum Circuit

Quantum circuits are constructed by combining quantum gates and applying them to specific qubits. A quantum circuit is a visual representation of the sequence of gate operations performed on the qubits to carry out a quantum algorithm. The arrangement and order of gates in a quantum circuit determine the computation being performed.

D. Quantum Algorithms

Quantum algorithms are designed to solve specific computational problems. Prominent examples include Shor's algorithm for factoring large numbers, Grover's algorithm for unstructured search, and the quantum phase estimation algorithm for simulating quantum systems. These algorithms utilize the unique properties of quantum systems to perform computations more efficiently than classical algorithms.

E. Quantum Measurement

At the end of a quantum computation, the qubits are measured to obtain the result. Measurement collapses the superposition of qubit states into classical bits, yielding a specific outcome with a certain probability. The probabilities of different measurement outcomes are determined by the quantum state of the qubits before measurement. Multiple measurements may be performed to gather statistical information.

F. Quantum Error Correction

Due to their extreme sensitivity to noise and outside interference, quantum systems are susceptible to errors in qubit operations that can have an impact on the computation.

The field of quantum error correction is an essential area of study that aims to provide methods for mistake detection and correction to guarantee the stability and dependability of quantum computing. This involves encoding information redundantly and implementing error-detection and error-correction protocols.

G. Quantum Hardware

Quantum computing requires physical systems that can realize qubits and perform quantum gate operations. Various technologies are being explored, such as superconducting circuits, trapped ions, topological qubits, and photonic qubits. Advances in quantum hardware are crucial for scaling up quantum computers and reducing noise and error rates.

IV. ALGORITHMS/TECHNIQUES

In order to solve computational problems more quickly than conventional algorithms, quantum computing and quantum algorithms are specially created algorithms that make use of the ideas of quantum physics. These algorithms execute parallel computations and simultaneously explore various possibilities by utilizing the features of quantum systems, such as superposition and entanglement. Here are a few notable quantum algorithms

A. Grover's Algorithm

Grover's algorithm is a quantum search algorithm that can search an unstructured database faster than classical algorithms. It provides a quadratic speedup over classical search algorithms, making it useful for problems like finding an entry in an unsorted list or solving certain optimization problems.

B. Shor's Algorithm

Shor's algorithm is a breakthrough quantum algorithm for factoring large numbers exponentially faster than the best-known classical algorithms. It has significant implications for breaking cryptographic systems based on integer factorization, which are widely used in modern security protocols.

C. Quantum Fourier Transform

The Quantum Fourier Transform is a quantum counterpart of the classical discrete Fourier transform and is a key component of many quantum algorithms. It allows for the transformation of information from the time domain to the frequency domain, enabling efficient quantum signal processing and algorithms like Shor's algorithm.

D. Variational Quantum Eigensolver

Variational Quantum Eigensolver is an algorithm designed for solving quantum chemistry problems. It utilizes quantum computers to simulate the behavior of molecules and find their ground-state energy. VQE combines classical optimization techniques with quantum computations to approximate the lowest energy state of a molecule.

E. Algorithms for Quantum Machine Learning

Numerous quantum machine learning techniques, including quantum principal component analysis, quantum k-means clustering, and quantum support vector machines, have been proposed. These methods seek to improve traditional machine learning tasks, such as dimensional reduction, clustering, and classification, by utilizing the capabilities of quantum computing.

F. Quantum Simulations

Quantum computers can simulate quantum systems more efficiently than classical computers. This capability is valuable for studying the behavior of molecules, materials, and quantum phenomena. Quantum simulations can provide insights into chemical reactions, quantum magnetism, superconductivity, and other complex quantum systems.

V. TOOLS AND TECHNOLOGIES

There are several tools and technologies used in the field of quantum computing. Here are some key ones:

A. Quantum Processor

Quantum processors are the physical devices that manipulate and store quantum information, represented by qubits. Different technologies are used for implementing quantum processors, including superconducting circuits, trapped ions, topological qubits, and photonics.

B. Quantum Development Kits/Frameworks

Quantum development kits provide software frameworks, libraries, and tools for programming quantum computers. These kits often include simulators for testing and debugging quantum algorithms and interfaces for interacting with quantum hardware. Examples include Qiskit, IBM Quantum Experience, Microsoft Quantum Development Kit, and Cirq.

C. Quantum Programming Languages

Quantum programming languages are designed specifically for expressing quantum algorithms and computations. These languages offer abstractions and constructs to work with qubits, quantum gates, and quantum operations. QASM (Quantum Assembly Language) and Q# (Q Sharp) are examples of quantum programming languages.

D. Quantum Simulators

Quantum simulators are software programs that simulate the behavior of quantum systems on classical computers. They enable researchers and developers to test and verify quantum algorithms before running them on actual quantum hardware. Examples include Qiskit's Aer, Google's Cirq simulator, and QuTiP.

E. Quantum Control and Measurement Device

These devices are used to manipulate and measure qubits in quantum processors. They include microwave and radiofrequency generators, control electronics, cryogenic systems for cooling the quantum hardware, and sensitive detectors for qubit measurement.

F. Quantum Error Correction Tools

As mentioned earlier, error correction is crucial in quantum computing. Tools and algorithms are being developed to detect and correct errors in quantum computations. These tools include error-correcting codes, error-detection circuits, and quantum error correction software.

G. Quantum Networking Equipment

Quantum networking involves the transmission and distribution of quantum information between quantum computers or quantum devices.

Specialized equipment, such as quantum repeaters, quantum memories, and quantum communication hardware, are being developed to enable secure and efficient quantum communication.

H. Quantum Cryptography Systems

Quantum cryptography systems utilize quantum properties for secure communication. These systems typically involve devices like quantum key distribution (QKD) systems, which generate and distribute cryptographic keys using quantum principles.

I. Quantum Machine Learning Libraries

Quantum machine learning combines quantum computing with machine learning techniques. Libraries and frameworks, such as TensorFlow Quantum (TFQ) and Pennylane, provide tools and interfaces for designing and implementing quantum machine learning models.

J. Quantum Software Development Environments

Integrated development environments (IDEs) tailored for quantum computing help streamline the development and debugging of quantum programs.

They often include features such as code editors, code visualization, and debugging tools. Examples include Microsoft Quantum Development Kit with Visual Studio, Qiskit Aqua, and PyQuil with Forest.

VI. CURRENT/LATEST WORKS IN FIELDS

Quantum computing is a rapidly evolving field with ongoing research and development worldwide. Here are some areas of current focus in quantum computing research:

A. Quantum Supremacy

Researchers are working towards achieving quantum supremacy, which refers to the ability of a quantum computer to perform tasks that are infeasible for classical computers. This milestone was achieved in 2019 by Google's Sycamore quantum processor, which solved a problem that would take classical computers thousands of years to solve.

B. Error Correction

Quantum systems are prone to errors caused by decoherence and external disturbances. Error correction techniques are being developed to mitigate these errors and improve the reliability of quantum computations. This involves encoding information redundantly and implementing error-detection and error-correction algorithms.

C. Quantum Algorithms

Researchers are exploring and creating quantum algorithms that, in comparison to conventional algorithms, can solve complicated problems more quickly by utilizing the special qualities of quantum systems. Grover's method for unstructured search and Shor's technique for factoring big numbers are two examples.

D. Quantum Simulation

Quantum computers have the potential to simulate and model quantum systems more accurately than classical computers. This has applications in materials science, drug discovery, optimization problems, and understanding fundamental physics. Research is focused on developing efficient simulation algorithms and improving the scalability of quantum simulations.

E. Cryptography at the Quantum Level

There are special prospects for safe communication in quantum mechanics. The goal of quantum cryptography is to create unbreakable cryptographic protocols, including quantum key distribution (QKD), based on the ideas of quantum physics. Scientists are attempting to create scalable and useful quantum cryptography systems.

F. Hardware in Quantum

One of the most important aspects of quantum computing research is the development of scalable and dependable quantum hardware. Superconducting qubits, photonics, trapped ions, and topological qubits are among the technologies being investigated. Enhancing qubit coherence times, lowering error rates, and increasing the qubit count are the three main goals of research.

G. Quantum Networking

Connecting multiple quantum computers through quantum networks is essential for distributed quantum computing and secure communication. Research focuses on developing protocols for quantum communication, quantum repeaters, and quantum network architectures.

H. Quantum Computational Learning

Research is now being conducted in the area where machine learning and quantum computing converge. Quantum machine learning aims to harness quantum properties to enhance learning algorithms and solve complex pattern recognition problems more efficiently.

I. Quantum Software and Programming

Developing quantum programming languages, compilers, and software tools is crucial for facilitating the programming and optimization of quantum algorithms. Efforts are underway to create user-friendly frameworks and programming interfaces for quantum computing.

J. Quantum Ethics and Policy

As quantum technologies advance, there is a growing need to address the ethical, societal, and policy implications of quantum computing. Research is exploring the potential impact of quantum computing on areas such as cryptography, Cybersecurity, privacy, and economic sectors.

VII. METHODOLOGY

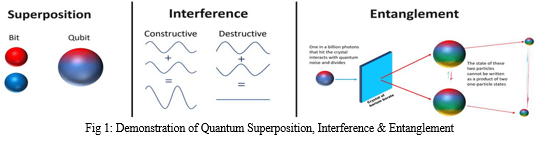
A. Superposition

It is a property of quantum systems that allows a qubit, the basic unit of information in quantum computing, to exist in a combination of multiple states simultaneously. Unlike classical bits, which can only be in a state of 0 or 1, a qubit in superposition can be in a state that is a linear combination of 0 and 1. To illustrate this concept, imagine a qubit represented as a particle that can be in a state of spinning up or spinning down.

In classical physics, the particle's spin would be either up or down. However, in quantum physics, the particle can exist in a superposition of both spinning up and spinning down at the same time. Superposition allows quantum computers to process information in parallel, exploring multiple possibilities simultaneously. This property is leveraged in quantum algorithms to perform computations more efficiently for certain tasks compared to classical computers. By applying quantum gates and operations to qubits in superposition, quantum algorithms can manipulate and transform the qubit states, ultimately yielding the desired result. The ability to process information in parallel through superposition is one of the key advantages of quantum computing and forms the basis for many quantum algorithms and their potential for exponential speedup in specific computational problems.

B. Quantum entanglement

It is a phenomenon in which two or more qubits become intrinsically linked in a way that their states are interdependent. When qubits are entangled, the measurement of one qubit instantaneously affects the state of the other qubits, regardless of the distance between them. To illustrate this concept, imagine two qubits that are entangled. If you measure the state of one qubit, the outcome of that measurement will be completely random. However, the result of the measurement will be correlated with the state of the other qubit. Even if the qubits are physically separated, when you measure the second qubit, its state will be found to be directly related to the result of the first qubit's measurement. This correlation is what makes entanglement a powerful resource in quantum computing. It allows for the transmission of information in an instantaneous and non-local way, which can be leveraged in various quantum algorithms and protocols. One notable application of entanglement is quantum teleportation, where the state of one qubit can be transmitted to another qubit instantaneously, without physically moving the qubit itself. This process relies on the entanglement between two qubits and classical communication to recreate the state of the original qubit in a different location. Entanglement is a crucial resource for quantum computing, enabling the implementation of quantum algorithms that take advantage of the interconnectedness and parallelism provided by entangled states. It plays a fundamental role in quantum communication, quantum cryptography, and quantum teleportation, among other areas of research and development in quantum computing.

C. Quantum interference

It is a phenomenon that arises due to the nature of superposition in quantum systems. When qubits are in a superposition of states, their combined states can interfere with each other, leading to interesting effects. To illustrate quantum interference, let's consider a thought experiment with a quantum system represented by a qubit. Imagine that this qubit is in a superposition of the states |0⟩ and |1⟩, where |0⟩ represents a particle being in one state and |1⟩ represents it being in another state. When these two states are superimposed, they can interfere with each other. Depending on the relative phase or alignment of the states, interference can be constructive or destructive. Constructive interference occurs when the two states are aligned in a way that their amplitudes add up, resulting in an enhanced signal or a higher probability of measuring a particular outcome. This reinforcement occurs when the phases of the two states are in sync, leading to a larger amplitude at that specific outcome. On the other hand, destructive interference occurs when the phases of the superimposed states are misaligned, causing their amplitudes to cancel out or diminish. This interference results in a reduced probability of measuring a particular outcome. Quantum interference is a fundamental concept that enables the manipulation and control of probabilities in quantum systems. It forms the basis for many quantum algorithms, such as quantum Fourier transform-based algorithms and quantum algorithms for solving optimization problems. By carefully designing and manipulating the superposition of quantum states and leveraging interference effects, quantum algorithms can exploit the constructive interference to enhance the desired outcomes and suppress undesired ones, leading to computational advantages over classical algorithms. It's important to note that while quantum interference is a powerful concept, its practical implementation and control depend on various factors, including the coherence and stability of the quantum system and the ability to manipulate and measure qubits with high precision.

VIII. CONCERNS

Although quantum computing has a lot of promise, there are several significant concerns associated with its development and implementation. Here are some of the key concerns:

A. Fragility of Qubits

Qubits are highly sensitive to environmental disturbances, making them susceptible to errors and decoherence. Maintaining the delicate quantum states of qubits for a sufficiently long time is a major technical challenge. Error correction techniques and fault-tolerant designs are being developed to mitigate these issues, but they add complexity and overhead to quantum systems.

B. Scalability

Building large-scale, practical quantum computers is a formidable task. Currently, quantum computers have a limited number of qubits, typically in the range of tens to hundreds. Scaling up to thousands or millions of qubits while maintaining their coherence and reducing error rates is a significant engineering hurdle that needs to be overcome.

C. High Resource Requirements

Quantum computers often require specialized and sophisticated hardware, such as superconducting circuits or trapped ions, which operate at extremely low temperatures. These requirements result in high costs, complex infrastructure, and significant power consumption, making it challenging to make quantum computing accessible and economically viable.

D. Limited Applicability

Quantum computers excel at solving specific types of problems, such as factoring large numbers or simulating quantum systems. However, they may not provide significant speedups or advantages for many other computational tasks that are well-suited for classical computers. Identifying practical applications where quantum computers can outperform their classical counterparts remains an active area of research.

E. Security Implications

Quantum computing presents a risk to current cryptography methods even though it has the ability to solve complicated problems. Large numbers can be factored efficiently by Shor's algorithm, a quantum computation that may make popular encryption techniques like RSA susceptible.

To protect sensitive data, new quantum-resistant encryption techniques must be developed.

F. Impacts on Society and Ethics

Ethical questions are raised by quantum computing, just like with other sophisticated technology. It might make simulations quicker and more effective, which could have an impact on the creation of novel substances, medications, or even armaments. The effects of quantum computing on labor markets, financial systems, and social dynamics are also being discussed and researched.

IX. ACKNOWLEDGMENT

I would like to express my sincere gratitude to Prof. Jigar Bhawsar, our guide, for his invaluable guidance, support, and encouragement. His extensive knowledge, experience, and feedback were instrumental in shaping the project and ensuring its success.I would also like to extend my heartfelt thanks to the staff and faculty of MCA, for their support and assistance during this project. Their expertise and resources were indispensable in making this project a reality. Finally, I would like to thank my family for their unwavering love, support, and encouragement, which have been a constant source of inspiration and motivation for me.

Conclusion

To sum up, quantum computing is at the vanguard of technological advancement, providing previously unheard-of computational capacity and having the potential to completely transform several industries, including material science, cryptography, and optimization. In this research study, we have investigated the basic ideas of quantum mechanics that drive quantum computing and looked at the field\'s status, highlighting both the field\'s impressive advancements and upcoming difficulties. It\'s clear from researchers\' continued exploration of the limits of quantum computing that interdisciplinary cooperation and consistent investment in R&D will be necessary to realize its full potential. The potential of quantum computing to solve intricate issues that are unsolvable for conventional computers is alluring, even if there are still many formidable obstacles to overcome. As we continue to explore the world of quantum computing. It is evident that a new era in computation is about to dawn, one that could fundamentally alter how we address and resolve some of the most important problems confronting humanity.

References

[1] Santanu Ganguly. \"Quantum Machine Learning: An Applied Approach\", Springer Science and Business Media LLC, 2021 [2] Vladimir Silva. \"Practical Quantum Computing for Developers\", Springer Science and Business Media LLC, 2018 [3] Jules Tilly, Hongxiang Chen, Shuxiang Cao, Dario Picozzi et al. \"The Variational Quantum Eigensolver: A review of methods and best practices\", Physics Reports, 2022 [4] \"Quantum Machine Learning\", Walter de Gruyter GmbH, 2020 [5] Adrian Gepp. \"A review of procedures to evolve quantum algorithms\", Genetic Programming and Evolvable Machines, 06/2009

Copyright

Copyright © 2024 Kingkar Das. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.