Quantum Machine Learning: Bridging Quantum Computing and Artificial Intelligence

Abstract

This comprehensive article explores the burgeoning field of Quantum Machine Learning (QML), examining its foundational principles, key algorithms, and potential applications. We delve into the fundamentals of quantum computing, including qubits, quantum gates, and the challenges of quantum measurement and decoherence. The article provides an in-depth analysis of Quantum Support Vector Machines (QSVM) and Quantum Neural Networks (QNN), comparing them with their classical counterparts and highlighting their unique advantages and limitations. We investigate the promising applications of QML in material science, cryptography, and optimization problems, showcasing its potential to revolutionize drug discovery, secure communication, and complex problem-solving. The review also addresses the significant challenges facing QML, including hardware constraints, error correction, algorithm development, and integration with classical systems. By synthesizing current research and identifying future directions, this article offers a comprehensive overview of QML\'s transformative potential in artificial intelligence and computational science, while acknowledging the hurdles that must be overcome to fully realize its capabilities.

Introduction

I. INTRODUCTION

Quantum Machine Learning (QML) represents a groundbreaking fusion of quantum computing and machine learning, poised to revolutionize artificial intelligence by harnessing the power of quantum mechanics. This emerging field promises to solve complex problems with unprecedented efficiency, potentially outperforming classical algorithms in various domains [1]. As quantum hardware continues to advance, researchers are developing novel quantum algorithms that leverage quantum superposition and entanglement to enhance machine learning tasks.

This article explores two fundamental QML algorithms: Quantum Support Vector Machines (QSVM) and Quantum Neural Networks (QNN), and their potential applications in material science, cryptography, and optimization. By examining these cutting-edge techniques, we aim to provide AI researchers and practitioners with a comprehensive understanding of QML's current capabilities and future prospects, highlighting the transformative potential of this interdisciplinary field.

II. FUNDAMENTALS OF QUANTUM COMPUTING

A. Quantum bits (qubits) and superposition

Quantum computing is built upon the concept of quantum bits, or qubits, which are fundamentally different from classical bits. While a classical bit can exist in only one of two states (0 or 1), a qubit can exist in a superposition of both states simultaneously. This property is described by the quantum state |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex numbers satisfying |α|² + |β|² = 1. Superposition allows quantum computers to process multiple states concurrently, potentially leading to exponential speedups in certain computations.

B. Quantum gates and circuits

Quantum gates are the building blocks of quantum circuits, analogous to logic gates in classical computing. However, quantum gates operate on qubits and must be reversible and unitary. Common single-qubit gates include the Hadamard gate (H), which creates superposition, and the Pauli-X, Y, and Z gates. Multi-qubit gates, such as the controlled-NOT (CNOT) gate, enable entanglement between qubits. Quantum circuits are constructed by combining these gates to perform complex quantum operations and algorithms.

C. Quantum Measurement and Decoherence

Measurement plays a crucial role in quantum computing, as it collapses the superposition of a qubit to a classical state. This process is probabilistic, with the probability of measuring |0⟩ or |1⟩ determined by |α|² and |β|² respectively. Decoherence is a major challenge in quantum computing, referring to the loss of quantum information due to interactions with the environment. It limits the time available for quantum computations and necessitates error correction techniques [2].

III. QUANTUM SUPPORT VECTOR MACHINES (QSVM)

A. Classical SVM Recap

Support Vector Machines (SVMs) are powerful classical machine learning algorithms used for classification and regression tasks. They work by finding an optimal hyperplane that separates data points into different classes, maximizing the margin between the classes. SVMs can handle non-linear classification through kernel methods, which implicitly map data to higher-dimensional spaces [3].

B. Quantum implementation of SVM

Quantum Support Vector Machines (QSVMs) leverage quantum computing to enhance the performance of classical SVMs. QSVMs utilize quantum algorithms to perform computationally intensive parts of the SVM process, such as the kernel evaluation and optimization steps. One approach involves encoding the input data into quantum states and using quantum circuits to compute kernel functions more efficiently [4].

C. Advantages over classical SVM

QSVMs offer potential advantages over their classical counterparts, particularly for large-scale problems. They can provide exponential speedups in kernel evaluation and dimensionality reduction, allowing for faster processing of high-dimensional data. Additionally, QSVMs may be able to explore more complex feature spaces that are intractable for classical algorithms, potentially leading to improved classification accuracy [5].

D. Challenges and limitations

Despite their promise, QSVMs face several challenges. Current quantum hardware is limited by noise and decoherence, which can affect the accuracy of results. Scaling QSVMs to handle large datasets remains a significant challenge, as it requires maintaining coherence for longer periods.

Moreover, the quantum advantage may be problem-specific, and not all SVM tasks will benefit equally from quantum implementation.

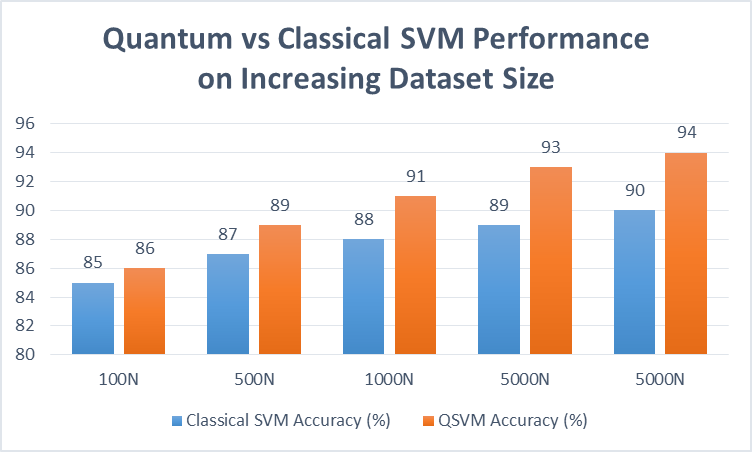
Fig 1: Quantum vs Classical SVM Performance on Increasing Dataset Size [4,5]

IV. QUANTUM NEURAL NETWORKS (QNN)

A. Classical neural network overview

Classical neural networks are machine learning models inspired by biological neural systems. They consist of interconnected layers of artificial neurons that process and transform input data to produce desired outputs. Deep neural networks, with multiple hidden layers, have achieved remarkable success in various tasks, including image and speech recognition.

B. Quantum states and operations in QNNs

Quantum Neural Networks (QNNs) incorporate quantum mechanics principles into neural network architectures. They use quantum states to represent and process information, leveraging superposition and entanglement. Quantum operations, such as unitary transformations and measurements, replace classical neural network operations. This allows QNNs to explore exponentially large state spaces and potentially capture more complex patterns in data [6].

C. Architectures of QNNs

Various QNN architectures have been proposed, including quantum circuit-based models and continuous-variable quantum neural networks. Some designs use variational quantum circuits as layers, where quantum gates with trainable parameters act on qubits. Others exploit quantum reservoirs, utilizing the natural dynamics of quantum systems for computation. Hybrid quantum-classical architectures, combining quantum and classical layers, are also being explored to leverage the strengths of both paradigms.

D. Potential performance enhancements

QNNs have the potential to outperform classical neural networks in certain tasks. They may offer advantages in terms of expressivity, allowing for more efficient representation of complex functions. QNNs could potentially process certain types of data more naturally, such as quantum data in quantum simulations or quantum sensing applications. Additionally, they might provide improved generalization capabilities and faster training for specific problem classes.

Table 1: Comparison of Classical and Quantum Machine Learning Algorithms [4-6]

V. APPLICATIONS OF QUANTUM MACHINE LEARNING

A. Material Science

1. Molecular simulations: Quantum Machine Learning (QML) shows great promise in revolutionizing molecular simulations. By leveraging quantum algorithms, researchers can more accurately model complex quantum systems, such as molecules and materials, at scales that are computationally infeasible for classical computers. QML techniques can enhance the prediction of molecular properties, including electronic structure, reactivity, and spectroscopic characteristics. This capability has far-reaching implications for materials design, potentially accelerating the discovery of new materials with desired properties for applications in energy storage, catalysis, and nanotechnology [7].
2. Drug discovery: In the pharmaceutical industry, QML has the potential to dramatically accelerate the drug discovery process. By employing quantum algorithms to simulate molecular interactions and predict drug efficacy, researchers can screen vast libraries of compounds more efficiently. QML can improve the accuracy of binding affinity predictions between drug candidates and target proteins, potentially reducing the time and cost associated with traditional drug discovery pipelines. This approach could lead to the identification of novel therapeutic compounds and personalized medicine strategies.

B. Cryptography

1. Quantum key distribution: Quantum Key Distribution (QKD) is a secure communication method that uses quantum mechanics principles to generate and distribute cryptographic keys. QML algorithms can enhance QKD protocols by optimizing the quantum states used for key generation and improving error correction techniques. This can lead to increased key generation rates and improved resilience against noise and eavesdropping attempts, ultimately resulting in more secure communication systems.
2. Post-quantum cryptography: As quantum computers threaten to break many classical encryption schemes, post-quantum cryptography aims to develop algorithms resistant to both classical and quantum attacks. QML can assist in the design and analysis of post-quantum cryptographic systems by exploring vast solution spaces more efficiently. Machine learning techniques can be applied to optimize key generation, enhance the security of lattice-based cryptosystems, and develop novel quantum-resistant encryption methods.

C. Optimization problems

1. Traveling salesman problem: The Traveling Salesman Problem (TSP) is a classical NP-hard optimization problem with applications in logistics, circuit design, and genome sequencing. Quantum algorithms, such as the Quantum Approximate Optimization Algorithm (QAOA), combined with machine learning techniques, show promise in finding near-optimal solutions to TSP instances more efficiently than classical methods. QML approaches can potentially handle larger problem sizes and provide better approximations, leading to significant improvements in various industries relying on routing and scheduling optimizations [8].
2. Portfolio optimization: In finance, portfolio optimization involves selecting the best asset allocation to maximize returns while minimizing risk. QML algorithms can potentially outperform classical methods in solving complex portfolio optimization problems, especially when dealing with large numbers of assets and considering various constraints. By leveraging quantum superposition and entanglement, QML techniques can explore a broader range of possible portfolio configurations simultaneously, potentially leading to more optimal investment strategies and improved risk management in financial markets.

Table 2: Applications and Challenges of Quantum Machine Learning [7,8]

VI. CHALLENGES AND FUTURE DIRECTIONS

A. Hardware limitations

Current quantum hardware faces significant challenges in terms of scalability, coherence times, and gate fidelities. Most quantum processors have a limited number of qubits, typically fewer than 100, which restricts the size and complexity of problems that can be tackled. Additionally, quantum states are highly sensitive to environmental disturbances, leading to short coherence times and high error rates. Overcoming these hardware limitations is crucial for realizing the full potential of quantum machine learning algorithms.

B. Error correction and noise mitigation

Quantum error correction (QEC) and noise mitigation techniques are essential for building fault-tolerant quantum computers capable of running complex QML algorithms. While theoretical frameworks for QEC exist, implementing them on current noisy intermediate-scale quantum (NISQ) devices remains challenging. Developing practical and efficient error correction methods, as well as noise-resilient algorithms, is a key area of ongoing research.

C. Algorithm development and benchmarking

As the field of quantum machine learning evolves, there is a pressing need for the development of new algorithms that can demonstrate clear quantum advantages over classical counterparts. This includes identifying problem classes where quantum algorithms can provide exponential speedups or qualitative improvements. Standardized benchmarking protocols are also crucial to accurately assess the performance of QML algorithms across different hardware platforms and compare them with classical methods.

D. Integration with classical systems

The future of quantum machine learning likely lies in hybrid quantum-classical systems that leverage the strengths of both paradigms. Developing efficient interfaces between quantum and classical components, optimizing data encoding and decoding strategies, and creating software frameworks that seamlessly integrate quantum and classical resources are important challenges. Additionally, exploring ways to use quantum processors as accelerators for specific subtasks within larger classical machine learning pipelines could lead to practical near-term applications [9].

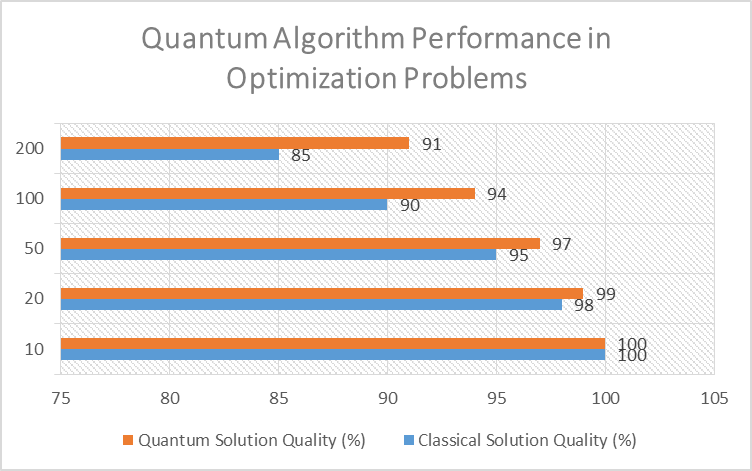
Fig 2: Quantum Algorithm Performance in Optimization Problems [9]

Conclusion

In conclusion, Quantum Machine Learning represents a frontier of immense potential at the intersection of quantum computing and artificial intelligence. This article has explored the fundamental concepts of QML, focusing on Quantum Support Vector Machines and Quantum Neural Networks, and their promising applications in fields such as material science, cryptography, and optimization. While QML offers tantalizing possibilities for exponential speedups and enhanced problem-solving capabilities, it also faces significant challenges, including hardware limitations, error correction, and algorithm development. As quantum technologies continue to advance, the integration of quantum and classical systems will likely play a crucial role in realizing practical QML applications. The future of QML depends on collaborative efforts across disciplines to overcome current obstacles and harness the full power of quantum mechanics for machine learning tasks. As research progresses, QML has the potential to revolutionize AI, opening new avenues for scientific discovery and technological innovation that were previously unattainable with classical computing alone.

References

[1] J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, and S. Lloyd, \"Quantum machine learning,\" Nature, vol. 549, no. 7671, pp. 195-202, Sep. 2017. [Online]. Available: https://www.nature.com/articles/nature23474 [2] F. Arute et al., \"Quantum supremacy using a programmable superconducting processor,\" Nature, vol. 574, no. 7779, pp. 505-510, Oct. 2019. [Online]. Available: https://www.nature.com/articles/s41586-019-1666-5 [3] C. Cortes and V. Vapnik, \"Support-vector networks,\" Machine Learning, vol. 20, no. 3, pp. 273-297, Sep. 1995. [Online]. Available: https://link.springer.com/article/10.1007/BF00994018 [4] V. Havlí?ek et al., \"Supervised learning with quantum-enhanced feature spaces,\" Nature, vol. 567, no. 7747, pp. 209-212, Mar. 2019. [Online]. Available: https://www.nature.com/articles/s41586-019-0980-2 [5] P. Rebentrost, M. Mohseni, and S. Lloyd, \"Quantum support vector machine for big data classification,\" Physical Review Letters, vol. 113, no. 13, p. 130503, Sep. 2014. [Online]. Available: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.113.130503 [6] K. Beer et al., \"Training deep quantum neural networks,\" Nature Communications, vol. 11, no. 1, p. 808, Feb. 2020. [Online]. Available: https://www.nature.com/articles/s41467-020-14454-2 [7] K. Bharti et al., \"Noisy intermediate-scale quantum algorithms,\" Reviews of Modern Physics, vol. 94, no. 1, p. 015004, Feb. 2022. [Online]. Available: https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.94.015004

Copyright

Copyright © 2024 Sunny Guntuka. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.