Queuing Theory in Traffic Management System

Abstract

In cities where the number of vehicles has consistently expanded faster than the transportation infrastructure available to serve them. More on queuing theory and its crucial application has been discussed in the current study. In Thudiyalur, Gandhipuram, and Periyanaickenpalayam, all in Coimbatore, this research examines the usefulness of queuing theory in the field of traffic management. The concept of traffic intensity is applied to a set of areas in queuing theory in this study.

Introduction

I. INTRODUCTION

Operations research (OR) is a discipline that focuses on the use of advanced analytical tools to aid in decision- making. Furthermore, operational analysis is an integral aspect of capabilities creation, management, and assurance in the British (and some British Commonwealth) military. Operational analysis is a component of the Combined Operational Effectiveness and Investment Appraisals, which aid in the procurement of British defence capability. The mathematical study of waiting lines, or queues, is known as queuing theory. The study of queues deals with measuring the phenomenon of waiting lines using representative measures of performances, such as average queue length , average waiting time in queue and average facility utilization. A queuing model is constructed so that queue lengths and waiting time can be predicted. Queuing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. This methodology is applicable in the field of Business, Industries, Government, Transportation, Restaurants, and Library etc. Queues arise when the short term demand for service exceeds the capacity. The Mathematical analysis of queues and waiting times in stochastic systems is called Modeling theory or Queuing theory.

II. MATERIALS AND METHODS TRAFFIC INTENSITY

The average occupancy of a server or resource for a particular period of time, usually a busy hour, is referred to as traffic intensity. It is defined as the ratio of the time a facility is cumulatively occupied to the time it is available for occupancy and is measured in traffic units

Some applications of traffic management systems are:

1. Automated Traffic Management System (ATMS): Manage the flow of road traffic using a variety of technologies.
2. E-tolls: Electronic toll booths deduct toll payments without stopping.
3. Electronic Road Pricing (ERP): Requires drivers to pay different tolls at different times.
4. Traveller Information System: provides online, real- time information on road condition.
5. Route Guidance System: Helps a driver navigate the best routes to a given location.

III. STRUCTURES AND CLASSIFIACTION OF QUEUING THEORY:

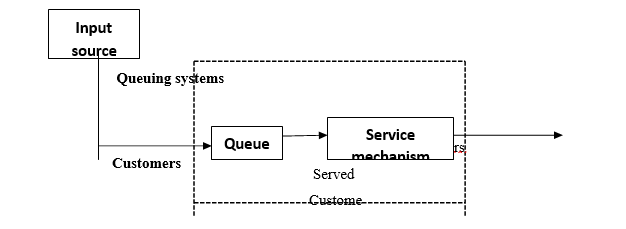
A. Characteristics of Queuing System

In designing a good queuing system, it is necessary to have a good information about the model. The characteristic listed below would provide sufficient information,

• Arrival pattern
• Server pattern
• Number of servers
• Queuing discipline

1. Arrival Pattern: This is the manner in which arrivals occur, indicted by the inter-arrival time between any two consecutive arrivals. For our stochastic modelling framework, the inter-arrival time may vary and may be described by a specific probability distribution that best describes the arrival pattern observed.

• Mean Arrival rate (λ): The mean arrival rate in a waiting line situation is defined as the expected number of arrivals occurring in a length unity. We define λ to be the arrival rate, which will have units of arrivals per hour

2. Service Pattern: This is the manner in which the service is rendered and is specified by the time taken to complete a service. Similar to the arrival pattern, distribution of the service time must be specified under stochastic modelling considerations.

• Mean service Rate (µ): The mean service rate is defined as the expected number of services completed in a time interval of length unity. We define µ to be the service rate is the expected number of customers that can be served by one of the servers per unit time

3. Number of Servers: The number of servers that are being utilize should be specified and in the manner. They work as a parallel servers or a series server has to be specified

4. Queuing Discipline

The most common queue disciplines are:

• First in first out(FIFO)
• First in last out (FILO)
• Served in random order(SIRO)
• Priority scheduling
• Processor sharing

B. The Single Server Poisson Queue Model (M/M.I) : (FIFO/∞)

The M/M/I is a Markovian model, where a solitary server is taken into concern. The model is the most rudimentary of queuing models. In this model we assume that appearance follows a Poisson distribution and administration times have an exponential distribution.

In this model we assume the appearance rate λ and administrative rate µ. Discipline followed here is first in first out that is there is no need arrangement for an appearance on help. There is no limit to the number of users the services provided works at their full capacity and the services rate is independent of the line length. The M/M/I model is viewed as steady just if λ > µ. On the off chance that on an average arrival happens quicker than services completion the queue will develop uncertainity long and the framework won’t have a stationary distribution

IV. FORMULAS

A. Traffic Intensity

The average number of customers being served is the ratio of arrival and service rate (i.e.) p = ????

????

For a stable system the service rate µ should always exceed the arrival rate λ and thus ρ should always be less than one. Therefore, it is also known as utilization factor of the server.

B. Average Number of Customer in the System

The average number of customer in the system is equal to the average number of customer in the queue together with those being serviced.

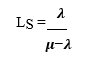
C. Average Number of Customer in Queue

It can be viewed as average queue length that is, the average number of customers who are waiting in the queue. It is defined as

D. Average Time Spent in the System

The average time spent in the system is equal to the total time that a customer spends in a system i.e. waiting time plus the service time. It is given by

E. Average Waiting Time in Queue

The average waiting time in queue is the average time a customer waits in queue forgetting service. It is expressed as

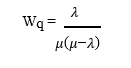
V. RESULT AND DISCUSSION

A. Tabulation

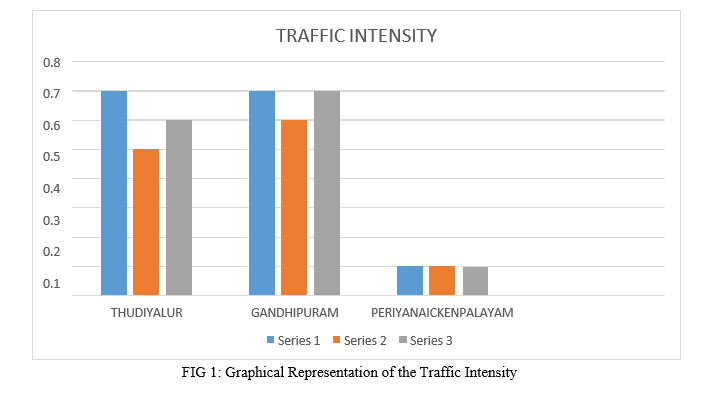
By using the different parameters stated in this paper on the basis of queuing theory we represent the traffic flow of traffic in the cities of Thudiyalur , Gandhipuram , and periyanickenpalayam .

TABLE -1

Table 2

VI. RESULT/ ANALYSIS

A. Morning Session

The arrival and service rate in the traffic intensity suggests an insecure traffic scenario, but not a particularly smooth flow of traffic.

B. Afternoon Session

In the afternoon session, the arrival and service rate in traffic intensity indicates an unstable and steady flow of traffic.

C. Evening Session

In the evening traffic session, the arrival and service rate suggest a somewhat consistent but unsmooth traffic flow

VII. ACKNOWLEDGEMENT

Thank you to S. REKHA, Assistant professor in Department of Mathematics at Dr SNS Rajalakshmi College of Arts and Science which has supported this research

Conclusion

The morning session, when commuters are reporting for work/business, and the evening session, when work/business is finished, are the busiest times, according to this study, especially on Thudiyalur, Gandhipuram, and Periyanaickenpalayam. As a result, additional time at junctions for traffic onto such routes is required during the morning and evening sessions. Increased traffic signal time reduces traffic intensity, resulting in less delays on such routes/channels during morning and evening rush hours Steps to reduce traffic congestion include: 1) Improving traffic light management, 2) Improving bus perceptions, and 3) Enforcing existing road traffic laws.

References

[1] Dr. jozsef Biro Doctor of the Hungarian Academy of science, Full professor Budapest university of technology and economics. Dr Zalan Herger P.h.D. Associate professor Budapest University of Technology and economics [2] Journal of physics in “Research on marginal cost model of electric vehicle charging and swapping facilities based on queuing theory” Laxin Hu and Tyler Yue 2021. IP Address 122.178.90.208 [3] Journal of Elsevier in “A short review on queuing theory as a deterministic tools in sustainable telecommunication system “ s.a afolalu, o.m ikumapayi , a. abulkareem , m.emetere , o.adejumo” journal available at www.elsevier.com/locate/matpr. [4] Journal of IOP conference series in “Application of queuing theory to reduce waiting period at ATM using in simulated approach” S. Devi Soorya and k.sreelatha 2021 IOP Conf.Ser:.mater.sci.eng.1145012041 [5] International journal of science in “The uses of queuing theory in management of traffic intensity” International journal of science Rowland jerry okecukwu ekocha and ikechi lhebom journal available in https//www.researchgate.net/publication/324194203. [6] Research Scholar J.J.T.University Rajasthan “Application of queuing theory in traffic management system” sathish agnihotri .ISSN – 2455 6602. [7] Further Applied Mathematics “The assessment of bank service performance in delta State Nigeria: A queuing theory Approach” Charles Okechukwu Aronu , Jophet Ewere okoh , Godspower onyekachukwc Ekwueme Vincent ikemefuna sol- Akubude. www.furthersci.com.

Copyright

Copyright © 2022 Divya. P, S. Rekha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.