An Overview on Several Types of the Optical Interferometers

Abstract

A common research instrument in many branches of science and engineering is the interferometer. Because they can identify and analyse interference patterns caused by the combination of light sources, these mid- to late-19th-century technologies are known as interferometers. The tool used for this process is called a \"interferometer\" or \"interfere-meter.\" Interferometers are remarkably versatile devices that enable the development of highly accurate optical sensors for a wide range of applications. This article discussed the principles of interferometry as well as three different interferometer configurations. The chosen configuration will be influenced by the machinery, mechanical stability, laser coherence, and particular goals. Interferometers are widely used in lab-on-a-chip systems for non-invasive biomolecule research, astronomy, and gravitational wave detection. [2].

Introduction

I. INTRODUCTION

A measurement technique called interferometry makes use of the phenomenon of wave interference (typically of radio, light, or sound waves). Certain properties of the waves themselves as well as the materials the waves interact with may be measured. Furthermore, methods for studying displacement changes using light waves are referred to as interferometry. In precision machining, displacement measurement interferometry is widely utilised for calibration and mechanical stage motion control. [1]An interference pattern can be created when two light beams are used, usually by splitting one beam into two. These two beams can then superimpose on each other. Due to the very short wavelength of visible light, even minute variations in the optical paths the distances travelled by the two beams can be detected since they will create discernible changes in the interference pattern. As a result, optical interferometry has been a useful measurement method for over a century. Later, when lasers were developed, its accuracy was increased.[1] Albert A. Michelson created the first interferometer in the 1880s, demonstrating the use of light interference principles as a measurement tool for the first time. The fundamental ideas of the Michelson interferometer continue to be at the heart of interferometry, despite advancements in technology as well as measurement precision) throughout time.[1]Two mirrors and a beamsplitter, or half-silvered mirror, make up a Michelson interferometer. The partially reflecting half-silvered mirror/beam splitter divides light into two beams with distinct optical paths, one of which is directed towards mirror 1 and the other towards mirror 2. These beams recombine at the beam splitter after being reflected back at the mirrors and before they reach the detector. An interference fringe pattern is produced by the phase difference between these two beams' different paths. Depending on what measurement the interferometer was being used for, the detector then analyses this pattern to determine the wave characteristics, material qualities, or displacement of one of the mirrors.[1] Having a single, extremely stable wavelength source is crucial for producing an interference pattern with great precision (distinct fringes), and the XL-80 laser helps achieve this Although there are other interferometer configurations based on Michelson's theory, the most straightforward to comprehend is the linear configuration.The two mirrors in the Michelson interferometer of the XL-80 laser system are retroreflectors, which are prisms that return incident light in a direction perpendicular to its original direction. One of these is fastened to the reference arm's beam splitter. As its distance from the beam splitter changes, the other retroreflector produces the variable length measurement arm. [1]After exiting the XL-80 laser head, the laser beam (1) splits into two beams at the polarising beam splitter: (1) reflected beam and (2) transmitted beam. Before reaching the detector, these beams are recombined at the beam splitter after being reflected back from the two retroreflectors. When the beams from the reference and measurement arms recombine at the beam splitter, the employment of retroreflectors guarantees that the beams are parallel. When the recombined beam reaches the detector, it either constructively or destructively interferes with one another. The two beams are in phase during constructive interference, and their peaks reinforce one another to produce a bright fringe. In contrast, during destructive interference, the beams are out of phase, and the peaks of one beam cancel out the troughs of the second beam, producing a dark fringe.[1]

These two beams' interference may be seen thanks to the detector's optical signal processing. The two beams' relative phases alter as a result of the measurement arm's displacement. The intensity of the recombined light varies cyclically as a result of this cycle of constructive and destructive interference. Every time the measurement arm/retroreflector is moved by 316.5 nm, or half the laser wavelength, the optical path changes by 633 nm, or the laser wavelength, resulting in one cycle of intensity variation from light to dark to light. As a result, the movement is quantified by utilising the following formula to get the number of cycles [1]:

d = Nλ/2

where N is the number of fringes crossed, λ is the laser's wavelength (0.633 microns), and d is the displacement (measured in microns). Phase interpolation during these cycles provides the better resolution of 1 nm.

The accuracy with which the laser beam's wavelength is understood determines how accurate and stable the laser unit is, as it has no bearing on how accurate the linear positional measurements are. The refractive index of the air that the laser beam travels through determines its operating wavelength, and this value varies with air temperature, air pressure, and relative humidity. Consequently, any changes in these parameters require adjustment in terms of compensation of the beam's wavelength.[1]

II. THEORY OF INTERFEROMETERS

A series of optical systems known as Iterferometers can be tailored for a variety of uses, including pathogen identification, the detection of liquid changes brought on by contaminants or oxygen depletion, and the correction of atmospheric aberrations. The idea of superposition, which allows two or more waves to occupy the same space at the same time, is a crucial characteristic of waves, such as light. Unlike particles that collide when they attempt to occupy the same space at the same time, this is a crucial property of all waves. When waves overlap, each overlapping wave gets added as a whole. Interference is a term commonly used to describe the superposition of two or more waves[2].

Three possible outcomes result from two waves travelling in the same direction and having equal characteristics in terms of amplitude and frequency.

Constructive interference occurs when both waves are in phase, matching each other's crests and valleys; destructive interference occurs when both waves are out of phase, causing the crest of one wave to coincide with the valley of the other; and neither constructive nor destructive interference occurs when there is a phase delay between the waves, meaning the waves are neither in nor out of phase. As it turns out, interference plays a significant role in explaining a variety of physical phenomena, including harmonics, diffraction gratings, standing waves, resonance, hearing, and speech.[2]

One of the most widely used optical instruments is the interferer, which can be made reasonably easily and with very high precision. Essentially, an interferometer divides a light beam which is typically a laser beam into two parts which are a sensor beam and a reference beam. The reference beam will follow an optical path without changing. A change in the optical route will impact the sensor beam and cause it to travel through a new path. Parameters we wish to measure such as temperature, pressure, or gases is the source of that change.

When the beams are recombined on a screen, an interference pattern will be produced by the interference between the two beams [2]. Consider the scenario when you wish to quantify the amount of a gas present. The sensor beam of your interferometer is designed to pass through a small air-filled gas container that we may have. An empty container and a reference beam are used to calibrate the interferometer. The interference pattern serves as a benchmark against which to evaluate your findings. For  instance we add a gas to your container which can be nitrogen, contaminated air, or even a liquid changing the refractive index of the container. The optical path and interference pattern of the sensing beam will alter in a manner that is related to the optical characteristics of the element being measured.[2]

III. TYPES OF INTERFEROMETERS

Interferometers come in various varieties. The most popular ones are Fabry-Perot, Michelson, and Mach-Zehnder. Still, there is a longer number of possible configurations, and specialised performance can be obtained with a custom interferometer design. The most popular interferometer types and their performance characteristics are described. [2]

In Figure 1, a Mach-Zehnder Interferometer is displayed. Two beams are created from the collimated beam: a reference beam (RB) and a sensor beam (SB).  After bouncing off a mirror and travelling down separate, equal-length optical routes, the two beams are recombined using a beam splitter.  One detector, often a CMOS camera, may then identify the interference pattern.[2]

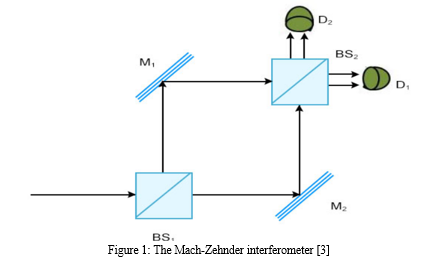
One kind of interferometer used to measure the relative phase shift between two collimated light beams is the Mach-Zehnder interferometer. With two beam splitters and two mirrors, it is also an amplitude-based beam division interferometer. Unlike the Michelson-Morley interferometer, the Mach-Zehnder interferometer recombines beams downstream of the second beam splitter, with each beam travelling a distinct path. Still, the coherent superposition of the two waves is what causes the interference.[3] At the first beam splitter, the incoming light is separated into two directions. Depending on the phase difference between the two waves, each beam reflects off a mirror before recombining at the end of the second beam splitter to create an interference pattern. One can purposefully introduce the phase difference, or analogous optical path, by making minimal modifications to one of the mirrors or beam splitters to produce a tiny asymmetry.[3]

If the difference between the two beams' optical path lengths is less than the light source's coherence length, interference fringes will be produced. The distance across which the light waves preserve their phase relationship is known as the coherence length. Interference fringes can be produced by constructive or destructive wave interference even when the two beams' optical path length differences are contained within the coherence length of the light source. In the interference pattern, these fringes appear as patterns of dark and light bands.[3] In order to guarantee that the two beams in the Mach-Zehnder interferometer have almost equal optical path lengths a feat made possible by the exceptionally small coherence lengths of light sources ,accurate parts and meticulous alignment are essential. Maintaining the interference fringes visibility and clarity requires this level of precision. It is possible to measure the difference in the optical path length caused by the sample by inserting it into one of the beam paths. The interference fringe changes are observed in order to obtain this measurement. These modifications reveal important details regarding the features and attributes of the sample under examination. Because it can detect even minute variations in optical path length, the Mach-Zehnder interferometer is an invaluable instrument for a wide range of scientific and technical uses.[3]

The Michelson interferometer holds a particularly distinctive place in the annals of physics.  It was created by Albert Michelson for use in the Michelson-Morley Experiment, one of the most well-known physics experiments in history.  The purpose of this experiment was to measure the variations in light speed as the earth went through space in order to identify the presence of luminiferous aether. The universe was meant to include aether, which would permit light to flow through it in the same way as sound waves require air to exist. The concept of aether's existence was disproved by Michelson and Morley, who were never able to measure any change in the speed of light.[2] The fact that gravitational waves were detected by the LIGO experiment using a Michelson interferometer is the second reason the MI is so important.  As previously stated, the LIGO experiment enables us to identify gravitational wave activity. Envision yourself in a forest, surrounded by a variety of plants, birds, and insects. Though you can recognise them and pick up on their habits, you never knew you had earplugs until someone took them out.  You can now hear the sounds of the birds, the wind blowing through the leaves, and a river you were unaware existed.  That is the extent of the LIGO experiment's relevance; it has given us a fresh perspective on cosmic exploration.[2]

A coherent light beam is split into two directions by the Michelson interferometer, a precision device, and after they have taken distinct optical routes, they are then combined again to create interference fringes. It divides a light beam into two or more segments and functions as a beam division interferometer as well. Two mirrors, a beam splitter, and a compensating plate make up the arrangement. In 1890, American scientist Albert A. Michelson created this amplitude-splitting apparatus. It is still a crucial instrument in contemporary labs, where it is frequently used to measure the wavelength of unknown light sources, detect minuscule distances, and research the characteristics of optical medium.[4]

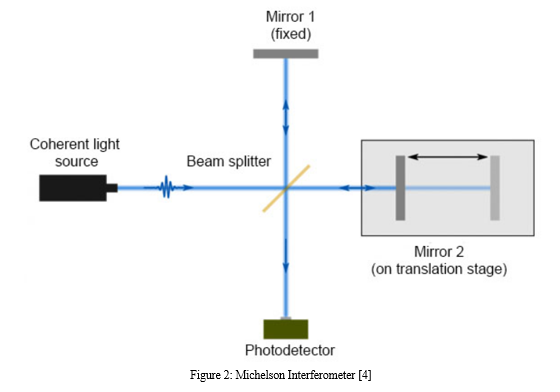
As shown in Figure 2, the Michelson interferometer is made up of three mirrors: a beam splitter (a semi-transparent mirror), a compensating glass plate, and two reflectors the very polished mirrors, M1 (fixed) & M2 (movable). The locations of M1 and M2 in relation to the beam splitter varies. The beam reflects back directly along the path it originally travelled because to the mirrors' precise alignment. At a 45° angle, the compensating glass plate and the beam splitter are positioned parallel to one another between the mirrors. The amplitude splitting is made possible by the beam splitter's opposing side, which is semi-silvered and evenly reflects and transmits light from the source.[4] A monochromatic source of light splits into two equally intense, perpendicular beams when it travels through the beam splitter. The mirror M1 receives half of the light that strikes the beam splitter and  reflects it back to the observer via the beam splitter. As shown in Figure 2, the transmitted half of the original beam travels towards the observer via the beam splitter after being reflected back by the mirror, M2. Fringes can be seen when coherent beams interfere with one another either destructively or constructively as they recombine at the beam splitter.[4]

Two flat surfaces with partially reflected mirrors make up the Fabry-Perot interferometer (Figure 5). There may be a tiny space between the surfaces that are facing one another.  One glass slab with slightly reflected surfaces can occasionally be used to form an FPI.[2] The beam splits on each reflection, converting the FPI into a multiple beam interferometer.The very high resolution of a multiple beam interferometer is one of its advantages just like a high number of lines/mm produces a high resolution diffraction grating. A very distinct interference pattern with a strong contrast between the light and dark fringes is achievable.FPI is used in many different contexts. The most popular method involves creating a laser with a very high quality factor Q using a Fabry-Perot cavity laser.[2]

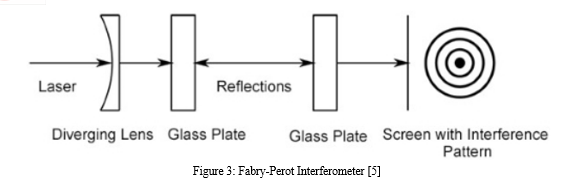
The multiple beam interference theory underpins the operation of the high-resolution Fabry-Perot Interferometer. A phenomenon known as multiple beam interference happens when several coherent light beams interact with one another and create an interference pattern. It is used to measure exact wavelengths, analyse two wavelengths that are very close to one another, calculate the refractive index of gases, calibrate standard metre scales based on wavelengths, and more.[5]

There are two very flat, parallel glass plates that make up the interferometer. They make a level space in the air between them. Eighty percent of the light is reflected by a glossy metal coating on the interior sides of the glass panels. The many reflections that occur between these plates are what allow the interferometer to function.[5] The thickness of the glass plates used in the interferometer varies, and the exterior of the plates are angled at a slight angle (~0.1º) in relation to the inner surfaces. This is done in order to remove any potential interference fringes from parallel, equally-inclined glass surfaces. With the use of a precision micrometre screw, one plate can be moved while the other is fixed. As a result, the air space between the plates is not as thick. A Fabry-Perot etalon is the name given to the device when both plates are stationary. Figure 5 depicts the Fabry-Perot interferometer configuration.[5]

Conclusion

Interferometers are incredibly adaptable devices that enable the development of highly precise optical sensors for a variety of uses. The fundamentals of interferometry and three distinct interferometer configurations were covered in this article. The equipment, mechanical stability, laser coherence, and specific objectives will all influence which configuration is used. Interferometers find extensive uses in astronomy, gravitational wave detection, and non-invasive methods for biomolecules in lab-on-a-chip systems.[2]. The interferometer is a widely used research tool in many fields of science and engineering. These technologies from the mid to late 19th century are called interferometers because they are able to recognise and interpret interference patterns that result from the combination of light sources. Interferometers are incredibly adaptable instruments that make it possible to create extremely precise optical sensors for a variety of uses. Three distinct interferometer configurations and the fundamentals of interferometry were covered in this study. The machinery, mechanical stability, laser coherence, and specific objectives will all have an impact on the arrangement that is selected. In lab-on-a-chip systems, interferometers are frequently utilised for gravitational wave detection, astronomy, and non-invasive biomolecule research. [2].

References

[1] https://www.renishaw.com/en/interferometry-explained--7854 [2] https://www.opticsforhire.com/blog/interferometers-types-performance-design-considerations/ [3] https://www.gophotonics.com/community/what-is-a-mach-zehnder-interferometer [4] https://www.gophotonics.com/community/what-is-a-michelson-interferometer [5] https://www.gophotonics.com/community/what-is-a-fabry-perot-interferometer

Copyright

Copyright © 2024 Muhammad Arif Bin Jalil. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.