The Next Frontier of Security: Homomorphic Encryption in Action

Abstract

Encryption is essential in preventing unauthorized access to sensitive data in light of the growing concerns about data security in cloud computing. Homomorphic encryption promises to enable secure calculations on encrypted data without the need for decryption, particularly for cloud-based operations. To evaluate the effectiveness and applicability of several homomorphic encryption algorithms for safe cloud computing, we compare and contrast them in this research paper. Partially homomorphic encryption (PHE), somewhat homomorphic encryption (SHE), and fully homomorphic encryption (FHE) are the three basic homomorphic encryption subtypes that we examine. The implications of this study can aid cloud service providers and organizations in selecting the most appropriate homomorphic encryption scheme based on their specific security requirements and performance considerations. The research contributes to the ongoing efforts to enhance data privacy in cloud computing environments, opening new possibilities for secure data processing in an increasingly connected digital world. The exploration of homomorphic encryption schemes in this study opens new avenues for research and development in the field of cryptographic techniques. As technology continues to evolve, so too must our approaches to safeguarding data. This research serves as a catalyst for further innovations in homomorphic encryption algorithms, enabling even more efficient and robust methods for secure data processing in cloud environments and beyond. The insights derived from this research paper not only empower cloud service providers and organizations to make informed decisions about selecting the most appropriate homomorphic encryption scheme but also contribute to the broader mission of fortifying data privacy and security in cloud computing.

Introduction

I. INTRODUCTION

Encryption plays a crucial part in keeping sensitive data secure in colourful operations and diligence. By converting information in plaintext format into cipher text using cryptographic algorithms, encryption protects data confidentiality and possession of the correct encryption keys, precluding unauthorized access and wiretapping.

Crucial operation is an integral part of encryption security because the strength of encryption depends on encryption keys being secure and accessible only to trusted individuals. In addition, encryption can also corroborate data integrity and ensure that data remains unchanged during transmission or storehouse.

By generating digital autographs or using vindicated encryption, encryption can reveal any unauthorized variations and save data integrity and responsibility.

Overall, encryption serves as an essential tool for guarding sensitive information and conserving data sequestration and integrity in a decreasingly connected and digital world. A ground-breaking idea that has transformed the area of cryptography is homomorphic encryption, promising to bridge the gap between data privacy and computational capabilities. In a world where data security and privacy are paramount concerns, homomorphic encryption emerges as a beacon of hope, offering a novel approach to protecting sensitive information [1].

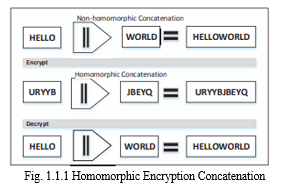
II. LITERATURE REVIEW

Security is a major requirement as cyber crimes are increasing nowadays. Today is a public environment to maintain data security. Many private environments are available, but saving data in these environments can be more expensive than in public flats. Therefore, it's convenient for everyone to store data in public the cloud, i.e. the Internet. There are many encryption algorithms available. With them, a safe environment is created. Homomorphic encryption enables this secure environment in which operations can be performed on the already encrypted data and the same result as on the original data can be obtained. There are many homomorphic encryption schemes described in this article that uses this approach. Homomorphic encryption, an innovative cryptographic concept, traces its roots back to the late 1970s when researchers Rivest, Adleman, and Dertouzos proposed a Multiplicative Homomorphic Cryptographic System based on the RSA algorithm. Despite this early introduction, homomorphic encryption has not gained much attention or practical use due to various problems and limitations. However, significant progress has been made in the following years. In the 1980s, Andrew Yao formally defined the idea of fully homomorphic encryption (FHE) and demonstrated the possibility of performing computations on encrypted data without decryption. The early 21st century saw increased interest and researchers focused on developing more practical semi-homomorphic encryption schemes. The big breakthrough came in 2009 when Craig Gentry's Ph.D. thesis revealed the first fully homomorphic encryption scheme based on lattice cryptography. Although the original scheme was computationally slow and not immediately suitable for real-world applications, it paved the way for further advances. During the 2010s, efforts were focused on improving the efficiency of homomorphic encryption with the development of partially and partially homomorphic encryption schemes, including the Brakerski-Gentry-Vaikuntanathan (BGV) scheme, which offered increased practicality for secure computation. In 2013, the release of the open-source library "HElib" by Craig Gentry andothers allowed researchers to experiment and innovate fully homomorphic encryption. Microsoft's implementation of "Microsoft SEAL" in 2014 further increased the performance and availability of homomorphic encryption for developers. IBM's "IBM Homomorphic Encryption Toolkit" in 2015 provided further R&D support in this area. As the technology matured, practical applications began to emerge. In 2016, Microsoft demonstrated the first real-world use case by securely analyzing medical data in the cloud using homomorphic encryption. Subsequently, this technique found application in finance, healthcare, secure machine learning, and other areas [2].

III. HOMOMORPHIC ENCRYPTION

A. Homomorphic Encryption Schemes

1. Partially Homomorphic Encryption (PHE):

Partially homomorphic encryption (PHE) allows the evaluation of a single type of mathematical operation on the encrypted data, either addition or multiplication. Although it does not support arbitrary calculations, it still has practical applications. The two main PHE schemes are:

A. Paillier Cipher: The Paillier cipher is a popular partially homomorphic encryption scheme based on number theory. Supports homomorphic addition on encrypted data. With Paillier, you can add two encrypted numbers and later decrypt the result to get the sum of the original numbers in plaintext.

B.ElGamal Encryption: ElGamal is another partially homomorphic encryption scheme that supports homomorphic multiplication on encrypted data. It allows an encrypted number to be multiplied by a plaintext number, resulting in a cipher text representing the product [3].

2. Somewhat Homomorphic Encryption (SHE):

Somewhat Homomorphic Encryption (SHE) allows multiple types of mathematical operations to be evaluated on encrypted data, but there are limitations. Although it provides more features than PHE, it is not fully capable of arbitrary calculations. The two main SHE schemes are:

A. RSA encryption (with appropriate padding): The RSA cryptosystem, when used with appropriate padding schemes such as OAEP (Optimal Asymmetric Encryption Padding), can support both homomorphic multiplication and addition on encrypted data. This allows users to perform limited calculations without decrypting the data.

B. Benaloh Cipher: Benaloh is another somewhat homomorphic encryption scheme that supports both homomorphic addition and multiplication. It is based on the RSA problem and the Decision Composite Residuality Assumption (DCRA) [3].

3. Fully Homomorphic Encryption (FHE):

Fully Homomorphic Encryption (FHE) is the most advanced and powerful type of homomorphic encryption. Unlike PHE and SHE, FHE allows arbitrary computations on encrypted data, meaning that any function that can be expressed mathematically can be performed on encrypted data without decryption. FHE enables end-to-end privacy for data processing. The two main FHE schemes are:

A. TFHE (Fully Homomorphic Encryption over the Torus): The TFHE scheme is based on lattice-based cryptography and provides full homomorphic capabilities to enable universal gate computations on encrypted data.

 B. BGV (Brakerski-Gentry-Vaikuntanathan) scheme: The BGV scheme is another fully homomorphic grid-based encryption that allows arbitrary computations on encrypted data.

It is essential to understand that while FHE provides the most comprehensive functionality, it comes with higher computational complexity, so practical implementations are currently less efficient compared to traditional encryption methods. Researchers continue to work on improving the performance of FHE to make it more viable for real-world applications [3].

B. Homomorphic Encoding Function

Homomorphic Encryption H is a set of four functions:

H = {Key Generation, Encryption, Decryption, Evaluation}

1. Key generation: the client will generate pair of keys public key pk and secret key sk for encryption of plaintext.
2. Encryption: Using a secret key sk client encrypts the plain text PT and generates Esk(PT) and along with public key pk, this cipher text CT will be sent to the server.
3. Evaluation: The server has a function f for doing an evaluation of cipher text CT and performed this as per the required function using pk.
4. Decryption: Generated Eval(f(PT)) will be decrypted by the client using its sk and it gets the original result.

Basic operations of homomorphic encryption:

a. Key Generation

• The process starts with a crucial generation step. A trusted authority generates a set of keys a public key and a  private key.
• The public key is used for encryption, while the private key is kept secret and is used for decryption

b. Encryption

• Suppose Alice wants to securely shoot a communication (plaintext) to Bob without revealing its contents. She uses Bob's public key to cipher the communication.
• The encryption process takes the plaintext and transforms it into cipher text using the public key.
• The performing cipher text is a representation of the translated communication and can be safely participated with anyone, including Bob.

c. Homomorphic Operations

• In a homomorphic encryption scheme, certain fine operations can be performed directly on the cipher texts, conserving the translated format.
• For illustration, let's assume the homomorphic encryption scheme supports addition as the homomorphic operation.

d. Addition

• Alice wants to perform an addition operation on two translated cipher texts without decoding them.
• She takes the two cipher texts, translated with Bob's public key, and performs the addition operation on them directly,   producing a newly translated cipher text as the result.
• The new cipher text represents the sum of the two original translated plaintexts.

e. Decryption

• Only Bob, who possesses the corresponding private key, can decipher the final result( the sum of the translated plaintexts) to gain the factual sum of the original plaintexts.
• No one differently, including Alice, gains any knowledge about the individual plaintext values during the calculation.

The process can be extended to support other homomorphic operations, similar to addition, depending on the type of homomorphic encryption scheme used [2].

IV. HOMOMORPHIC ENCRYPTION AND NETWORK CODING IN IOT ARCHITECTURES

The Internet of Things (IoT) has quickly spread throughout many industries, opening up new markets and enabling intelligent applications. Security and privacy issues, however, have become important growth hindrances for IoT. The security threats and requirement for improved protection grow along with the number of linked devices, especially for remotely monitored actuators. Homomorphic Encryption (HE), a novel encryption technique, has gained popularity as a solution to privacy issues. HE allows operations on encrypted data, in contrast to standard algorithms, assuring end-to-end dataflow privacy in IoT. It enables machine learning computations without requiring access to user data by enabling safe data storage in public clouds. However, this strategy results in network latency because it raises computing expenses and packet size. An effective way to address latency problems is by network coding or NC. Its characteristics aid distributed storage systems and wireless sensor networks (WSNs) by improving communication robustness and reducing latency in a variety of topologies. In order to examine the possibilities of this synergy, this article examines approaches fusing NC and HE within the IoT architecture. The IoT architecture under consideration consists of endpoint devices for data collection, a multi-cloud environment for storage and processing, and a middle network linking them. Achieving end-to-end privacy is possible using HE encryption. NC is integrated throughout the design to address issues about latency during data transmission and computation in the multi-cloud context. The combination of NC and HE provides a novel method for optimizing the IoT ecosystem, maintaining data privacy, and cutting down on communication lag for real-time applications [4].

1. Privacy-preserving IoT-based crowd-sensing network with comparable homomorphic encryption and its application in combating COVID-19

Privacy-preserving techniques for the crowd-sensing network have been a hot topic in recent years. Focusing on data privacy protection in mobile sensing, Wang et al introduced a framework called ARTSense. Based on such a framework, two privacy-preserving solutions were proposed to maintain reputation and trust in mobile sensing. In, a privacy protection mechanism was built in the crowd-sensing network based on the combination of dynamic trust management with the distribution of keys. By enabling privacy-preserving data processing and analysis, homomorphic encryption (HE) can play a critical role in the fight against COVID-19, especially in situations where sensitive health data needs to be gathered and shared for public health purposes. Here are some applications for homomorphic encryption:

a. Contact tracing: To locate and alert people who may have been exposed to COVID-19, contact tracing is crucial. Without compromising people's privacy, homomorphic encryption enables the secure capture and analysis of location and interaction data. In order to protect data privacy while still detecting prospective contacts, it enables health authorities to run contact tracing algorithms on encrypted data without first decrypting the personal information of the individuals.

b. Secure sharing of health data across various healthcare organizations and research institutes is made possible by homomorphic encryption. With Homomorphic Encryption, test results and medical records can be processed and encrypted without the need for decryption, shielding private information from prying eyes as it is being transmitted and analyzed.

c. Vaccine Distribution: Data on susceptible groups, infection rates, and vaccination coverage must be examined for effective vaccine distribution. In order to secure data aggregation and analysis without disclosing the raw data, homomorphic encryption is used, which promotes better vaccination distribution decisions.

d. Personalized Treatment: By enabling secure analysis of medical data while protecting patient privacy, HE can provide COVID-19 patients with personalized treatment options. Without disclosing sensitive patient health information, machine learning models can be trained on encrypted data and the findings utilized to create treatment regimens specifically for each patient.

e. Research Collaboration: Secure collaboration between researchers from various institutions is made possible by homomorphic encryption. Without distributing raw data, researchers can collaborate on the analysis of encrypted datasets, protecting data privacy while yet gaining from group intelligence.

f. Public Health Surveillance: Homomorphic encryption enables safe data aggregation from numerous sources, including clinics, hospitals, and testing facilities. While maintaining individual anonymity, this encrypted data can be used for analysis to track infection rates, pinpoint hotspots, and spot possible outbreaks.

These applications of homomorphic encryption enable public health authorities, academics, and healthcare providers to leverage the power of data analytics while guaranteeing the protection of individual privacy. It facilitates data exchange for better disease prevention and management while fostering public confidence [4].

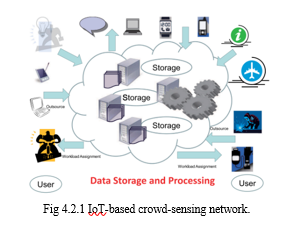
2. Privacy-Preserving Machine Learning with Homomorphic Encryption

Machine learning with privacy protection: Homomorphic encryption can be used to train and use machine learning models on data that has been encrypted. Applications like fraud detection, health diagnostics, and targeted advertising might all benefit from this.

Homomorphic encryption could be used in the context of fraud detection to train a machine learning model to recognize fraudulent transactions without the requirement to decode consumer financial information. This would enable the bank to safeguard consumer privacy while employing machine learning to combat fraud. For instance, a bank could encrypt the financial information of its clients before providing it with a machine-learning algorithm. Then, without having access to unencrypted data, a machine learning algorithm might make calculations on encrypted data. The bank might use the results of the calculations to spot fraudulent transactions once they had been decrypted. Homomorphic encryption could be utilized in the context of medical diagnosis to train a machine-learning model to identify diseases without the need to decode patient records. This will enable medical professionals to safeguard patient privacy while enhancing the standard of treatment through the use of machine learning. A healthcare practitioner might, for instance, encrypt patient medical records before feeding them to a machine-learning algorithm. Then, without having access to unencrypted data, a machine learning algorithm might make calculations on encrypted data. After deciphering the equations' results, the healthcare professional could utilize them to identify disorders [4].

V. KEY REDUCTION IN MULTI-KEY AND THRESHOLD MULTI-KEY HOMOMORPHIC ENCRYPTIONS BY REUSING ERROR

As cloud computing and AI as a Service are provided, it is increasingly necessary to deal with privacy-sensitive data. To deal with sensitive data, there are two cases of outsourcing process:

i) Many clients participate dynamically ii) many clients are pre-determined. The solutions for protecting sensitive data in both cases are the multi-key homomorphic encryption (MKHE) scheme and the threshold multikey homomorphic encryption (TMKHE) scheme. However, these schemes may be difficult for clients with limited resources to perform MKHE and TMKHE. In addition, due to the large size of the evaluation keys, in particular multiplication and rotation keys, the communication between the clients and server that provides outsourcing service increases. Also, the size of the evaluation keys that the server must hold is tremendous, in particular, for the multiplication and rotation keys, which are essential for bootstrapping operation. In this paper, we propose a variant of MKHE and TMKHE with reduced evaluation keys. To reduce the size of the evaluation keys, we propose a variant of ring learning with errors (RLWE), called RRLWE reusing errors (ReRLWE). ReRLWE generates other components by reusing the error that is used when generating an RLWE sample. We prove that RLWE can be reduced to ReRLWE and propose modified evaluation keys under the ReRLWE assumption, which are the modified multiplication and rotation keys.For MKHE, multiplication, and rotation keys are reduced by 66% and 25%, respectively. For TMKHE, multiplication, and rotation keys are reduced by 50% and 25%, respectively[6].

1. Multikey Verifiable Homomorphic Encryption

A homomorphic encryption (HE) scheme is an advanced encryption technology that allows any user receiving cipher texts to perform computations over them in a public manner. An important application of an HE scheme is a private delegating computation where clients encrypt their secret data and send the cipher texts to (computationally powerful) server thatperforms computations over encrypted data. In this application, one of the crucial problems is that the delegated server might be not a trusted one and in this case, we can't believe that a server always returns correct computation results. To solve this problem, Lai et al. (ESORICS 2014) proposed verifiable homomorphic encryption (VHE) as a core primitive realizing private and verifiable secure delegating computation. However, their VHE scheme only supports homomorphic evaluation over cipher texts generated by a single user. In this paper, we propose formalization and its construction of multi-key verifiable homomorphic encryption (MVHE), which is anew cryptographic primitive for realizing private and verifiable delegated computation in the multi-client setting. Our construction can be obtained by combining a multi-key homomorphic encryption scheme and a multi-key homomorphic encrypted authentication scheme, which is also a new primitive provided in this work [7].

2. A Framework for Privacy-Preserving Multi-Party Skyline Query Based on Homomorphic Encryption

Nowadays, the management and analyses of ‘big data’ are becoming indispensable for numerous organizations all over the world. In many cases, multiple organizations want to perform data analyses on their combined databases. Skyline query is one of the popular operations for selecting representative objects from a large database, where any other object within the database does not dominate each of the representative objects, called ‘skyline’. Like other data analytics operations, the multi-party skyline query can provide benefits to the participating organizations by retrieving the skyline objects from their combined databases. Such a multi-party skyline query demands the disclosure of individual parties’ objects to others during the computation. But, owing to the data privacy and security concern of the present IT era, such disclosure of the individual parties’ databases is strictly prohibited.

Considering this issue, we are proposing a new framework for the privacy-preserving multi-party skyline query, exploiting additive homomorphic encryption along with data anonymization, perturbation, and randomization techniques. The underlying protocols within our proposed framework ensure that every participating party can identify its multi-party skyline objects without revealing the objects to others during the multi-party skyline query. The detailed privacy and security analyses show that the proposed framework can achieve the desired computational without privacy leakage. Besides, the performance evaluation through complexity analyses, extensive simulations, and comprehensive comparison also demonstrates the utility and efficiency of the proposed framework [8].

3. Cyber-Security Enhancement of Networked Control Systems Using Homomorphic Encryption

Cyber-security of the networked control system is one of the significantly important issues in the control engineering area because the networked control system is applied to the industrial and critical infrastructures such as water, transportation, and electricity networks. There are several approaches such as the model-based detection methods, risk management for the threats, and protections of the signals transmitted over the communication channels, in order to enhance the cyber-security against malicious users and adversaries. The authors are interested in how to prevent malicious users and adversaries from monitoring and stealing the information to operate the control system, in terms of cryptography. Cryptography is an important technology enabling to the protection of information against third parties such as malicious users and adversaries, and recently public-key cryptography is in widespread use in cloud systems. For example, the RSA encryption system, named after its inventors Rivest, Shamir, and Adleman, is the first public-key encryption system in widespread use and is still important to learn. The ElGamal encryption system is the more secure public-key encryption system, and actually is used in the free GNU privacy guard, the digital signature algorithms. In such a public-key encryption scheme, the public key generated by some party severs as an encryption key; anyone who knows that public key can use it to encrypt messages and generate corresponding cipher texts[9].

4. Efficient Levelled (Multi) Identity-Based Fully Homomorphic Encryption Schemes

The first identity-based fully homomorphic encryption (IBFHE) scheme was constructed from identity-based encryption (IBE) and lattice-based cryptography by Gentry, Sahai, and Waters in CRYPTO2013. Their IBFHE scheme is improved in this paper, exploiting Alperin–Sheriff and Peikert’s tight and simple noise analysis method when evaluating homomorphically and Micciancio and Peikert’s powerful and novel trapdoor. Furthermore, using the masking scheme (Mukherjee and Wichs in EUROCRYPT 2016), we construct an efficient multi-identity fully homomorphic encryption (MIFHE) scheme by expanding afresh’’ cipher text under a single identity key to an ‘‘expanded’’ one under a combined key that enables cipher texts under different identities to be homomorphically evaluated [10].

5. Fidelity Preserved Data Hiding in Encrypted Images Based on Homomorphism and Matrix Embedding

Data hiding in images is a scheme that hides a secret message in a cover image. It can be used to send secret message through the cover image or embed important information, such as copyright information, authentication information, or management information into the cover image. In the past decade, many data-hiding schemes have been proposed. Schemes embedded the data in the spatial domain. Schemes implemented the data hiding in the compressed domain. Recently, a new technology called data hiding in encrypted images (DHEI) has become an interesting notion in the data hiding arena. Considering such an application, in a cloud storing and computing system, a user will send the encrypted images to the cloud server to protect the private data. For data management, this process still requires that the server can embed the messages, such as copyright information or authentication message, in uploaded encrypted images. The DHEI technology just meets the requirements [11].

6. Health data privacy through homomorphicencryption and distributed ledger computing:an ethical-legal qualitative expert assessment study

Background: Increasingly, hospitals and research institutes are developing technical solutions for sharing patient data in a privacy-preserving manner. Two of these technical solutions are homomorphic encryption and distributed ledger technology. Homomorphic encryption allows computations to be performed on data without this data ever being decrypted. Therefore, homomorphic encryption represents a potential solution for conducting feasibility studies on cohorts of sensitive patient data stored in distributed locations. Distributed ledger technology provides a permanent record of all transfers and processing of patient data, allowing data custodians to audit access.

A significant portion of the current literature has examined how these technologies might comply with data protection and research ethics frameworks. In the Swiss context, these instruments include the Federal Act on Data Protection and the Human Research Act. There are also institutional frameworks that govern the processing of health-relatedand genetic data at different universities and hospitals. Given Switzerland’s geographical proximity to European Union (EU)member states, the General Data Protection Regulation (GDPR) may impose additional obligations.Methods: To conduct this assessment, we carried out a series of qualitative interviews with key stakeholders at Swiss hospitals and research institutions. These included legal and clinical data management staff, as well as clinical andresearch ethics experts. These interviews were carried out with two series of vignettes that focused on data discovery using homomorphic encryption and data erasure from a distributed ledger platform.Results: For our first set of vignettes, interviewees were prepared to allow data discovery requests if patients had provided general consent or ethics committee approval, depending on the types of data made available. Our interviewees highlighted the importance of protecting against the risk of re identification given different types of data. For our second set, there was disagreement amongst interviewees on whether they would delete patient data ]locally, or delete data linked to a ledger with cryptographic hashes. Our interviewees were also willing to delete data locally oron the ledger, subject to local legislation [12].

7. He-Booster on Multiple GPUS

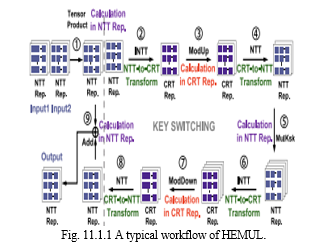
 In supercomputing and cloud scenarios, multiple GPUs are usually integrated with the same high-performance server node. Thus, it is worth investigating the FHE acceleration on multi-GPU systems. A straightforward method is assigning different FHE operations to different GPUs in an operation-level granularity. Essentially, this is a task-scheduling mechanism. Instead, this paper focuses on accelerating a single FHE operation on multiple GPUs because such fine-grained parallelization is critical for a scalable design. Among the homomorphic operations, homomorphic multiplication (HEMUL) and homomorphic rotation (HEROT) suffer from significantly higher computation overhead than homomorphic addition (HEADD). Both HEMUL and HEROT require computationally expensive key-switching operations to maintain the cipher text, which dominates the cost of the entire workflow. In contrast, HEADD only involves simple polynomial-wise addition with negligible computation cost. Therefore, it is critical to figure out how to execute key switching operations in parallel on multiple GPUs for overall performance gain. Further, due to the commonality, this paper primarily takes HEMUL as an example to present our design. As we can see from the typical workflow of HEMUL in Fig. 8, HEMUL mainly involves the calculation of several polynomials in different representations (e.g., CRT and NTT representations). Actually, these polynomials are transformed from original coefficient matrices. And the size of each matrix is large and can thus be partitioned for parallel execution. Therefore, in the case of the acceleration on multiple GPUs, the opportunities come from the tremendous data-level parallelism provided by those large coefficient matrices, which can be exploited to map the same task on multiple GPUs to process different data partitions. Note that HE-Booster on a single GPU primarily exploits the thread-level parallelism, such as the local synchronization in the NTT phase. And the task running on each GPU still applies the single-GPU acceleration design. Since the polynomials represented by coefficient matrices are usually accessed with different patterns or granularity, three typical partitions on data-level parallelism are accordingly adopted in HE-Booster for different stages [13].

8. Secure Fully Homomorphic Authenticated Encryption

Homomorphic authenticated encryption allows implicit computation on plaintexts using corresponding ciphertexts without losing privacy and provides the authenticity of the computation and the resultant plaintext of the computation when performing decryption. However, due to its special functionality, the security notions of homomorphic authenticated encryption are somewhat complicated and the construction of fully homomorphic authenticated encryption has never been given. In this work, we propose a new security notion and the first construction of fully homomorphic authenticated encryption. Our new security notion is a unified definition of data privacy and authenticity of homomorphic authenticated encryption. Moreover, our security notion is simpler and stronger than the previous ones. To realize our new security notion, we also suggest a construction of fully homomorphic authenticated encryption via generic construction. We combine a fully homomorphic encryption and two homomorphic authenticators, one fully homomorphic and one OR-homomorphic, to construct a fully homomorphic authenticated encryption that satisfies our security notion. Our construction requires its fully homomorphic encryption to be indistinguishable under chosen plaintext attacks and its homomorphic authenticators to be enforceable under selectively chosen plaintext queries. Our construction also supports multiple datasets and amortized efficiency. For efficiency, we also construct a multi-dataset fully homomorphic authenticator scheme, which is a variant of the first fully homomorphic signature scheme. Our multi-dataset fully homomorphic authenticator scheme satisfies the security requirement of our generic construction above and supports amortized efficiency [14].

9. Secure Outsourced Computation of Matrix Determinant Based on Fully Homomorphic Encryption

Fully homomorphic encryption enables to perform of arbitrary computation over encrypted data, providing a powerful tool for secure outsourced computation in an un trusted environment. This paper investigates secure outsourced computation of matrix determinants based on fully homomorphic encryption. We propose an efficient secure outsourced computation scheme for matrix determinants based on an efficient matrix encoding technique called hypercube structure which packs a matrix into a single cipher text. Experimental results show that our scheme efficiently computes the matrix determinant in the cipher text domain. Finally, we show that our proposed scheme can be easily applied as a sub module in high-level applications.

Cloud computing offers users with scalable and on-demand access to computing resources saving them the cost of acquiring and maintaining their IT systems. Some well-known examples of cloud computing services are Google Drive, Amazon AWS and Microsoft Azure, and so on. Outsourced computation is one of the main services provided by the cloud computing paradigm, where a resource-constrained user may outsource data storage and processing task to the cloud server, and the latter returns the computational result back to the user. Outsourced computation utilizes the powerful capabilities of cloud computing, greatly reducing the local computation overhead. However, despite the great advantages offered by the outsourced computation paradigm, it also brings in some new challenges. The primary concern with outsourced computation is the client’s data privacy. As data involved in outsourced computation may include sensitive information, storing private data in the cloud server somewhere could pose a severe threat to data privacy as cloud service providers can directly access to the client’s data. Actually, the data privacy concern remains one of the main barriers to the widespread adoption of the cloud computing paradigm, according to the Cloud Security Alliance. While the client may choose to encrypt data with the traditional encryption techniques before outsourcing, the cloud servers can no longer perform any meaningful operations on the encrypted data. Therefore, it is highly desirable that while the cloud server provides the computing services, it cannot obtain any information about the client’s data. Fully homomorphic encryption (FHE)  enables us to perform arbitrary computations over encrypted data, which has great practical significance in the secure outsourced computation on an untrusted computation environment. Fully homomorphic encryption allows a weak client to securely delegate computation-intensive tasks to the cloud platform and thus greatly reduces the local computational overhead. As fully homomorphic encryption provides a general framework to compute any function on cipher texts, a variety of secure outsourced computation applications based on fully homomorphic encryption have been proposed in recent years, ranging from fundamental functions [15].

10. Secure Scheme for Locating Disease-Causing Genes Based on Multi-Key Homomorphic Encryption

Genes have great significance for the prevention and treatment of some diseases. A vital consideration is a need to find a way to locate pathogenic genes by analyzing the genetic data obtained from different medical institutions while protecting the privacy of patient’s genetic data. In this paper, we present a secure scheme for locating disease-causing genes based on Multi-Key Homomorphic Encryption (MKHE), which reduces the risk of leaking genetic data. First, we combine MKHE with a frequency-based pathogenic gene location function. Medical institutions use MKHE to encrypt their genetic data. The cloud then homomorphically evaluates specific gene-locating circuits on the encrypted genetic data.

Second, whereas most location circuits are designed only for locating monogenic diseases, we propose two location circuits (TH-intersection and Top-q) that can locate the disease-causing genes of polygenic diseases. Third, we construct a directed decryption protocol in which the users involved in the homomorphic evaluation can appoint a target user who can obtain the final decryption result. Our experimental results show that compared to the JWB+17 scheme published in the journal Science, our scheme can be used to diagnose polygenic diseases, and the participants only need to upload their encrypted genetic data once, which reduces the communication traffic by a few hundred-fold [16].

11. Separable Reversible Data Hiding Scheme in Homomorphic Encrypted Domain Based on NTRU

NTRU (Number Theory Research Unit) has the characteristics of resistance to quantum computing attacks, fast encryption and decryption, and high security. It is very suitable for wireless confidential data networks and authentication systems. Combined with reversible data hiding technology, a separable reversible data hiding scheme in a homomorphic encrypted domain based on NTRU is proposed. The image owner directly divides the cover image into groups of a reference pixel and T adjacent pixels. Then, the grouped image is encrypted by NTRU. Finally, the encrypted image is uploaded to the data hider. The encrypted image is divided into groups by the same grouping method as the image owner. After that, the data hider calculates the T absolute differences of adjacent pixels in each group to obtain a histogram of the absolute differences. The additional data can be embedded into the encrypted image by shifting the histogram of the absolute differences. After receiving the encrypted image with hidden data, the receiver can either use the data hiding key to directly extract the additional data from the encrypted domain to obtain the encrypted image or use the private key and data hiding key to extract the additional data from the plaintext domain to get the cover image. Experimental results show that our scheme has higher security and better embedding performance compared with other state-of-the-art works [17].

12. Verifiable Homomorphic Secret Sharing for Machine Learning Classifiers

When using machine learning classifiers to classify data in cloud computing, it is crucial to maintain data privacy and ensure the correctness of classification results. To address these security concerns, we propose a new verifiable homomorphic secret sharing (VHSS) scheme. Our approach involves distributing the task of executing a polynomial form of the machine learning classifier among two servers that produce partial results on encrypted data. Each server cannot obtain any data information, and the classification result can be reconstructed and verified using a verification key in conjunction with the two partial results. Compared to previous VHSS schemes, our scheme can compute the degree of polynomials as high as the polynomials in the system security parameters while performing comparably to homomorphic secret sharing (HSS) schemes. We implement our proposed scheme and demonstrate its application to decision trees (a type of machine learning classifier). Our experiments show that our scheme is twice as fast as previous VHSS schemes when evaluating decision trees with depths ranging from 2-14 [18].

13. Improved Homomorphic Discrete Fourier Transforms and FHE Bootstrapping

Homomorphic encryption (HE), which enables computation on ciphertexts without any leakage, rises as a most promising solution for privacy-preserving data processing, including secure machine learning and secure out-sourcing computation. Despite the extensive applicability of HE, the current constructions are sometimes considered impractical due to their inefficiency. In this paper, we propose improvements on the linear transformation in bootstrapping, a technique allowing the infinite number of operations for HE, and homomorphic discrete Fourier transformation (DFT) using batch homomorphic encryption. We observe that the multiplication of a sparse diagonal matrix and ciphertext of a vector can be done within O(1) homomorphic computations. This observation induces a faster algorithm for linear transformation in bootstrapping and homomorphic DFT. To achieve this, we use Cooley-Tukey matrix factorization andconstruct a new recursive factorization of the linear transformation in bootstrapping. Our method with radix r only requires O(r log n) constant vector multiplication and O( √ r log n) rotations by consuming O(log n) depth when the input vector size is n. The previous method used in the library, a library that implements homomorphic encryption for approximate computation, requires O(n) and O( √ n), respectively. To show performance improvement, we implement our method on top of the library. Our implementation, along with further techniques, of these algorithms shows significant improvements compared to the previous algorithm.

A new homomorphic DFT with length 214 only takes about 8s which results 150 times faster than the previous method. Furthermore, the bootstrapping takes about 2 minutes for C 32768 plaintext space with 8-bit precision, which takes 26 hours with the same bit precision using the previous method [19].

14. Precise Approximation of Convolutional Neural Networks for Homomorphically Encrypted Data

Homomorphic encryption (HE) is one of the representative solutions to privacy-preserving machine learning (PPML) classification enabling the server to classify the private data of clients while guaranteeing privacy. This work focuses on PPML using word-wise fully homomorphic encryption (FHE). In order to implement deep learning on word-wise HE, the ReLU and max-pooling functions should be approximated by polynomials for homomorphic operations. Most of the previous studies focus on HE-friendly networks, which approximate the ReLU and max-pooling functions using low-degree polynomials. However, this approximation cannot support deeper neural networks due to large approximation errors in general and can classify only relatively small datasets. Thus, we propose a precise polynomial approximation technique, a composition of minimax approximate polynomials of low degrees for the ReLU and max-pooling functions. If we replace the ReLU and max-pooling functions with the proposed approximate polynomials, standard deep learning models such as ResNet and VGGNet can still be used without further modification for PPML on FHE. Even pre-trained parameters can be used without retraining, which makes the proposed method more practical. We approximate the ReLU and max-pooling functions in the ResNet-152 using the composition of minimax approximate polynomials of degrees 15, 27, and 29. Then, we succeed in classifying the plaintext ImageNet dataset with 77.52% accuracy, which is very close to the original model accuracy of 78.31%. Also, we obtain an accuracy of 87.90% for classifying the encrypted CIFAR-10 dataset in the ResNet-20 without any additional training [20].

15. Significance of Homomorphic Encryption

Millions of customers' accounts on Sony's PlayStation network were compromised in April 2011 as a result of a hack into the system, exposing passwords, credit card numbers, and other personal data. Sony admitted responsibility for the event and acknowledged that other security measures, such as encrypting the data on their network, may have been implemented. Researchers learned that Dropbox was keeping user files that weren't protected around the same time. As a result, users who were upset that the corporation hadn't encrypted their private files terminated their accounts in protest. The problem these two businesses were having was not as easily resolved as one might think. First, the data needed to be decrypted before their customers and clients could use it. To accomplish this, the decryption key needed to be somewhere between the user and the data repository. The decryption key should be kept as near to the user and as far away from the data repository as possible. However, doing this without compromising the confidentiality of their client's data was quite challenging. For instance, Sony wanted a billing address so that they could charge customers' credit cards whether or not they were online. They still needed to store the decryption key on their servers even if the credit card details and addresses were encrypted. The decryption key had to be accessible to decrypt the data as soon as the consumer clicked "update account" if they provided an "update account" page with the address already filled in.There is therefore only so much protection encryption would have been able to offer if Sony's web server needed to be able to decrypt data and hackers broke into Sony's servers. Users are now able to outsource the storage and computation of their data to cloud services thanks to the advent of cloud storage platforms like Dropbox and computing platforms. Businesses are now increasingly using cloud services for data management and storage. Although they obtain these benefits, using cloud services may have disadvantages such as loss of privacy and the commercial value of secret data. Encrypting all data stored in the cloud and performing operations on the encrypted data is one practical solution to these challenges as well as Sony's problems. If the encryption method is homomorphic, the cloud can still use the data to make useful calculations even though the data is encrypted.

16. Multi-cloud computing privacy challenges using homomorphic encryption

When it comes to the security of user data in cloud computing, multi-cloud has numerous benefits. One of the issues that demand a lot of attention is multi-cloud security.

Security issues include isolation management, data exposure and confidentiality, VM security, trust, and unique security threats related to collaboration amongst cloud entities are hotly debated by academics and industry experts. In multi-cloud systems, trust, policy, and privacy in particular are important factors. In our plan, we'll put a lot of emphasis on protecting client data and identification.

Because it should not be disclosed to anybody who is not authorized to view it, cloud data privacy is essential.

There should be a strategy in place to guarantee data privacy and identification when data is stored across numerous clouds.Clients must conceal their identity from Cloud computing services when the volume of data is particularly sensitive in order to ensure anonymity. Appropriate data encoding techniques should be used to prevent unauthorized access while data is being transported and stored in the cloud services [22].

17. Applications of Homomorphic Encryption

Homomorphic encryption (HE) has various potential applications in different domains. Here are some key applications of homomorphic encryption:

a. National Security/Critical Infrastructure: HE can be employed to protect data from various nodes in critical infrastructure systems, such as smart grids. It ensures that computations on the data can be performed securely and remotely without the need to expose sensitive information[23].

b. Education: The use of homomorphic encryption can enable predictive analytics in the education sector without compromising data privacy. It allows for the secure computation of sensitive student information from various institutions, aiding in predicting student dropouts and designing interventions[23].

c. Smart Cities: Homomorphic encryption can play a crucial role in smart cities, where data from various sources need to be analyzed for route planning, emergency response, and infrastructure management without disclosing sensitive information[23].

d. Genomics: Homomorphic encryption can facilitate data sharing in genomics while preserving privacy. It allows researchers to perform computations on encrypted genomic data without the need to decrypt it, thus maintaining the confidentiality of sensitive genetic information[23].

e. Health: Homomorphic encryption can be utilized in healthcare applications to protect patient data while allowing computations for billing, reporting, and precision medicine. It enables secure analysis of sensitive medical records without revealing the actual data[24].

f. Control Systems/Cyber-Physical Systems: HE can be utilized to protect control systems from potential hacking attempts. Encrypting sensing data and control commands ensures data confidentiality and detection of unauthorized manipulations[25].

Conclusion

The ongoing advancements in homomorphic encryption schemes, such as Partially Homomorphic Encryption (PHE), Somewhat Homomorphic Encryption (SHE), and Fully Homomorphic Encryption (FHE), are driving the field toward more practical and efficient implementations. Given itsextensive functionality, researchers are actively attempting to enhance Fully Homomorphic Encryption\'s (FHE) performance tomake it more suitable for practical applications. Furthermore, the incorporation of homomorphic encryption and network coding in IoT designs opens up new opportunities for improving data privacy and lowering communication latency. Homomorphic encryption is at the fore as companies and organizations become more aware of the value of data security, offering a potential way to achieve both computational efficiency and data confidentiality in cloud computing and IoT ecosystems.

References

[1] Introduction to Homomorphic Encryption and Schemes Jung Hee Cheon, Anamaria Costache, Radames Cruz Moreno, Wei Dai,Nicolas Gama, Mariya Georgieva, Shai Halevi, Miran Kim, Sunwoong Kim,Kim Laine, Yuriy Polyakov, and Yongsoo Song. [2] Survey of Various Homomorphic Encryption Algorithms and Schemes by Payal V. Parmar Institute of Technology Bharuch,India.Shraddha B. Padhar Institute of Technology,Shafika N. Patel, Niyatee I. Bhatt,Rutvij H. Jhaveri [3] A Survey on Homomorphic Encryption Schemes by ABBAS ACAR, HIDAYET AKSU, and A. SELCUK ULUAGAC, Florida International University MAURO CONTI, University of Padua. [4] Privacy-preserving IoT-based crowd-sensing network with comparable homomorphic encryption and its application in combating COVID-19 Daxin Huang, Qingqing Gan, Xiaoming Wang, Marek R. Ogiela,Xu An Wang. [5] Homomorphic Encryption by Monique Ogburna*, Claude Turner, Pushkar Dahalc a,b,c Bowie State University, Department of Computer Science, 14000 Jericho Park Rd., Bowie, MD 20715, United States. [6] Key Reduction in Multi-Key and Threshold Multi-Key Homomorphic Encryptions by Reusing Error ZAHYUN KOO, JOON-WOO LEE, (Member, IEEE), JONG-SEON NO 1(Fellow, IEEE)AND YOUNG-SIK KIM (Member, IEEE). [7] Multikey Verifiable Homomorphic EncryptionYI LU 1,2, KEISUKE HARA2,3, AND KEISUKE TANAKA1 1Department of Mathematical and Computing Science, Tokyo Institute of Technology, Tokyo 152-8550, Japan,2.National Institute of Advanced Industrial Science and Technology (AIST), Tokyo 100-8921, Japan,3.Graduate School of Environment and Information Sciences, Yokohama National University, Yokohama 240-8501, Japan. [8] A Framework for Privacy-Preserving Multi-Party Skyline Query Based on Homomorphic EncryptionMAHBOOB QAOSAR KAZI MD. ROKIBUL ALAM ,ASIF ZAMAN,CHEN LI ,SALEH AHMED , MD. ANISUZZAMAN SIDDIQUE, AND YASUHIKO MORIMOTO. [9] Cyber-Security Enhancement of Networked Control SystemsUsing Homomorphic Encryption by Kiminao Kogiso and Takahiro Fujita. [10] Efficient Leveled (Multi) Identity-Based FullyHomomorphic Encryption SchemesTONGCHEN SHEN,FUQUN WANG,KEFEI CHENKUNPENG WANG (Member, IEEE), AND BAO. [11] Fidelity Preserved Data Hiding in Encrypted Images Based on Homomorphism and Matrix Embedding SISHENG CHEN CHIN-CHEN CHANG (Fellow, IEEE), AND QUNYING LIAO. [12] Health data privacy through homomorphic encryption and distributed ledger computing:an ethical-legal qualitative expert assessmentstudy James Scheibner Marcello Ienca1and Efy Vayena. [13] HE-Booster: An Efficient Polynomial Arithmetic Acceleration on GPUs for Fully Homomorphic Encryption Zhiwei Wang, Peinan Li, Rui Hou, Zhihao Li, Jiangfeng Cao, XiaoFeng Wang, and Dan Meng. [14] Secure Fully Homomorphic Authenticated Encryption JEONGSU KIM 1 AND AARAM YUN 2 1Department of Computer Science and Engineering, Ulsan National Institution. [15] Secure Outsourced Computation of Matrix Determinants Based on Fully Homomorphic Encryption HAORAN ZONG, HAI HUANG, AND SHUFANG WANG. [16] Secure Scheme for Locating Disease-Causing Genes Based on Multi-Key Homomorphic Encryption Tanping Zhou, Wenchao Liu, Ningbo Li, Xiaoyuan Yang, Yiliang Han, and Shangwen Zheng. [17] Separable Reversible Data Hiding Scheme in Homomorphic Encrypted Domain Based on NTRU NENG ZHOU, MINQING ZHANG, HAN WANG, YAN KE, AND FUQIANG DI. [18] Verifiable Homomorphic Secret Sharing for Machine Learning Classifiers XIN CHEN. [19] Improved Homomorphic Discrete Fourier Transforms and FHE Bootstrapping KYOOHYUNG HAN, MINKI HHAN, AND JUNG HEE CHEON. [20] Precise Approximation of Convolutional Neural Networks for Homomorphically Encrypted Data JUNGHYUN LEE 1 , (Graduate Student Member, IEEE), EUNSANG LEE 2 , JOON-WOO LEE 3 , (Member, IEEE), YONGJUNE KIM 4 , (Member, IEEE), YOUNG-SIK KIM 5 , (Member, IEEE), AND JONG-SEON NO 1 , (Fellow, IEEE) [21] Homomorphic Encryption by Monique Ogburna*, Claude Turner, Pushkar Dahalc a,b,c Bowie State University, Department of Computer Science, 14000 Jericho Park Rd., Bowie, MD 20715, United States [22] Handling security issues by using homomorphic encryption in the multi-cloud environment by Yulliwas Ameur, Samia Bouzefranea, Le Vinh ThinhbaCEDRIC Lab, Conservatoire National des Arts et Metiers (Cnam), Paris, France Faculty of Information Technology, HCMUTE, Ho Chi Minh, Vietnam. [23] APPLICATIONS OF HOMOMORPHIC ENCRYPTION David Archer, Lily Chen, Jung Hee Cheon, Ran Gilad-Bachrach, Roger A. Hallman,Zhicong Huang, Xiaoqian Jiang, Ranjit Kumaresan, Bradley A. Malin, Heidi Sofia,Yongsoo Song, Shuang Wang. [24] Achieving GWAS with homomorphic encryption by Jun Jie Sim, Fook Mun Chan, Shibin Chen, Benjamin Hong Meng Tan, and Khin Mi Mi Aung. [25] ]Health data privacy through homomorphic encryption and distributed ledger computing:an ethical-legal qualitative expert assessment study by James Scheibner, Marcello Ienca1and Efy Vayena1. [26] Cyber-Security Enhancement of Networked Control Systems Using Homomorphic Encryption by Kiminao Kogiso and Takahiro Fujita.

Copyright

Copyright © 2024 Prof. Shweta Sabnis, Prof. Pavan Mitragotri. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.