Ultra-High Birefringence Property and Low Confinement Loss of Circular Photonic Crystal Fiber for Telecommunication Application

Abstract

A redesigned PCF structure with minimal confinement loss and high birefringence is proposed in this research paper. It employs a circular lattice arrangement with one ring of identical air holes. High birefringence and low confinement loss are two of the properties that have been numerically studied using the finite element method with circular perfectly matched layer boundary conditions. By adjusting the hole size and spacing, it is possible to achieve both properties simultaneously. At an excitation wavelength of 1550 nm, a numerically obtained modal birefringence of 2.3179×10-2 is observed. Simultaneously, by methodically evaluating the cladding rings, the center-to-center distance between the air holes, and the number of cladding rings with equal diameters, a minimal confinement loss (<10-1) may be achieved. Additionally, the suggested PCF verifies that it is feasible to acquire. Our extremely birefringent fiber can be controllably created thanks to the development of birefringence with structural modifications. The suggested structure has better optical characteristics, making it a potential contender for sensing and broadband dispersion correction.

Introduction

I. INTRODUCTION

In terms of geometric parameters like hole-to-hole distance/spacing [1,2,3], pitch, air hole radius/diameter, and air filling fraction, photonic crystal fibers (PCFs), hole-fibers (HFs), and microstructure optical fibers (HFs) display a spectrum of unique optical properties that cannot be achieved with traditional optical fibers (COFs) technology. PCFs provide more leeway in adjusting birefringence, confinement loss [4], and dispersion [5,6] for any combination of air channels in the vicinity, all without doping the silica core [7].

Optical fibers made on a silica-air microstructure type are known as PCFs. The reduced refractive index cladding and small air holes in the silica backdrop run the length of the fiber [8]. It is typical for air holes to be positioned in periodic patterns inside the cladding, although they may also be hexagonal, octagonal, circular, or square. The central component might be solid (like a silica core) or hollow (like an air core). Just like traditional optical fibers (COFs), the first core type PCF uses a modified Total Internal Reflection (TIR) mechanism to steer light.

The latter employs a novel pathway called the photonic band gap (PBG) to direct light [9]. So, it's not strictly required for PCFs that the core and cladding be constructed of materials with high refractive indices. Additionally, it is not required that all optical fibers use TIR mechanisms to restrict light to their cores.

By including small air passages into the cladding of PCFs, a greater range of design options is available, allowing for tremendous property customization [10]. One may create guiding qualities tailored to a particular application by adjusting the parameters of the silica-air hole microstructure.

PCFs exhibit a wide range of peculiar and unfathomable characteristics, such as permanently operating in a single mode [11], very high or low nonlinearities [12], extremely high or low birefringence [13], extremely flattening and extremely low chromatic dispersion [14], and many more. Due to their better and readily modifiable optical qualities, PCFs may quickly surpass traditional optical fibers in several technical and scientific domains.

II. BACKGROUND AND METHODS OF PCF

A. PCF

An important step forward in optical technology is the development of photonic crystal fibers, also known as holey fibers (HFs). These fibers have a cladding that resembles a two-dimensional (open periodic) array of densely packed glass capillaries, which is drawn at a high temperature. Much research on the extraordinary characteristics of holey fibers has been going on since the first publications detailing their production in 1996 [1]. As the range of possible uses for these fibers continues to develop, more and more academic institutions are beginning to use holey fibers in their investigations. Such fibers are of great interest in the context of numerous optical fiber problems [2–13], nonlinearities properties [14–19], atomic optics [14,20,21], the physics of photonic crystals and quantum electrodynamics [20–24], biomedical optics [26], data transmission [18], super-sensitive gas sensors, microwave sensors, and other practical application areas. The optical fibers that are often used to transmit messages via light are usually constructed from two glasses. A cylindrical core made of solid glass with a higher refractive index runs along the center of the fiber, making it a waveguide. In order to provide a uniform covering for the core, another solid glass with a lower refractive index is used [5]. Silica (SiOz) is a common substance that both glasses are formed of. For silica glass to have a higher or lower refractive index, the element germanium or fluorine is often doped into the material [6]. By creating an index difference between the core and cladding, light may be guided down the fiber's length using total internal reflection (TIR) [7]. This helps to confine the light within the core. Conventional optical fiber describes this kind of fiber. While its current state of the art indicates extensive use in telecom and non-telecom applications, there are certain things that it just cannot perform. For such common fibers, the characteristics of the glass used in their production are the limiting factor [8]. Because silica glass has rigid characteristics, regular fibers aren't going to cut it for certain new uses. Photonic crystal fibers, also known as holey optical fibers (HOFs) or microstructure optical fibers (MOFs), were invented as a possible solution to the problems caused by traditional fibers and are now a staple in fiber-optics technology [9].

B. Evolution of PCF

After the first holey optical fiber was shown in 1996 by Knight et al. [17], the area of PCF research got underway. Holey fibers with periodic air-holes organized in a hexagonal lattice have been practically realized by them [18]. The researchers' first goal was to find a way to guide light using the PBG principle, but they ended up finding that the new holey fiber is more like regular fibers in that it uses a modified TIR mechanism, much like the old ones [9]. It wasn't long before they noticed the new fiber's durability and light-guiding efficiency. Coupled light is also simple to achieve. When comparing the traditional fibers with the PCFs, we found that they differed significantly in both design space and optical characteristics. Figure 2 shows how the PCF research area has grown rapidly in recent years [35]. Since only the most prominent journals are taken into account, the real quantity of papers is more than what is shown in the chart.

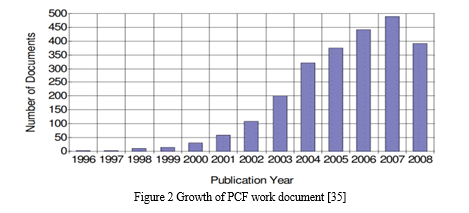
Thus, index guiding PCF research is ongoing; however, hollow core fibers were not yet feasible owing to the difficulty in creating enough big air holes in the fiber core to meet the dimensions necessary for PBG guidance. A breakthrough in numerical computation—the development of fully vectorially numerical methods—led to the 1978 demonstration of the Bragg fiber[41]. Research on PCF has made significant strides since its discovery in 1978, as shown in Table I [36].

TABLE I
Important milestones in the evolution of HFs

In the time after, it underwent extensive study by academics and industry professionals alike, and it is today a prominent area of electro-optical research [9, 20].

C. Inclination

One of the most significant developments in the history of fiber was the creation of the PCF [9]. It has ushered in an era of boundless opportunity and possibility. Many industrial and scientific applications in linear and nonlinear regimes rely on its exceptional optical features, which include a larger design space, flexibility, and superiority [9, 35]. According to predictions, PCFs and our investigation of their light-control possibilities hold the key to optics's bright future. In the medical field, for instance, new-wavelength lasers or broadband light sources are needed for diagnosis; in the telecommunications industry, more adaptable amplifiers and inexpensive, easy-to-install fibers are sought after; and in the sensor business, sensitive gas detector systems for both on-site and off-site monitoring are sought after. PCFs, with their hollow or solid cores, may function as optical components in all of these new industries [36]. These fibers are ideal for delivering high-power beams for laser cutting and welding since they may display much greater damage thresholds compared to traditional fibers. They have the potential to greatly improve environmental sensing by facilitating a number of nonlinear optical processes. Nevertheless, for a number of new uses, including power supply with ultra-short pulses and pulse compression, design and refinement of additional features are necessary. These features should ideally have enhanced bandwidth, near-zero flat chromatic dispersion, and nonlinear response control [9, 35, 36].

Great technical hurdles persist in doing these vital jobs. The next parts will provide a quick overview of some of these challenges, while the following chapters will go into more depth on them. Taking into account the aforementioned technical challenges and the boundless potential of this emerging area, I have chosen to contribute to the continuing endeavours of developing smart PCFs for a range of technological uses.

D. Applications Based on Dispersion Managed

Even though PCFs provide a lot of leeway in terms of design, designers still have a tough time creating nearly-zero dispersion-flat PCFs (NZDF PCFs), which are necessary for practically all applications [16, 21]. The reason is, that in addition to dispersion-flat features, minimal confinement loss is needed for the majority of dispersion-managed applications [21]. To obtain a dispersion-flat curve and low confinement losses at the same time, designers employ either PCFs with non-uniform cladding [23] or PCFs with multiple rings of air-holes [12] to decrease confinement losses. In addition to being inappropriate for managing wideband dispersion [23], the previous design method significantly increases the holey cladding area and makes manufacturing more difficult [24]. The second method reportedly poses a significant manufacturing challenge due to non-uniform cladding, despite its widespread usage. Increasing the number of design factors has a multiplicative effect on fabrication and tolerance when the cladding is not uniform, as is the case with air-hole modulation. Novel design strategies are necessary to solve these obstacles, which still remain today.

E. Non-linear Applications of PCFs

In the field of nonlinear optics, highly nonlinear PCFs (HNL-PCFs) have found many uses, including optical parametric amplification, wavelength converters, super continuum production, and soliton creation [25, 26]. Choosing an appropriate zero-dispersion wavelength around the telecom window is the most difficult part of designing highly nonlinear PCFs. This is because, on one hand, a PCF with a small pitch and uniformly small air holes will cause the zero-dispersion wavelength to move towards shorter wavelengths [26]; on the other hand, a PCF with a large air hole relative to its pitch will limit the bandwidth available for single mode operation [27]. For this reason, maximizing the air-hole diameter while simultaneously retaining architectural simplicity is of the utmost importance. As the pitch value of HNL-PCFs decreases, controlling confinement loss and being sensitive to changes in the parameters become significant challenges. A greater sensitivity to changes in parameters and a greater confinement loss are outcomes of a narrower pitch [28]. Up until this point, the same difficulty has persisted and requires effective resolution.

F. Applications as Sensor

Sensor applications are well-suited to highly birefringent PCFs, or HB-PCFs. It is necessary to impart pressures to the cladding or to disrupt the symmetry of the fiber axis in order to design extremely birefringent PCFs [29]. Problems with manufacturing and other issues with designing for low confinement losses and almost nil dispersion are brought on by such modifications to PCF claddings. This is because, according to the literature, birefringent fibers should exhibit almost negligible dispersion at the desired wavelength [30]. Because of the need of careful design, this is also a continuous problem.

G. Telecom Application

Optical device applications were the only ones first thought of while PCF technology was being studied, rather than data transmission medium. This occurred because these fibers had very large optical losses [31]. The optical losses have been brought down to 0.28 dB/km recently by using precise and high-tech methods of design and manufacture [32]. As a result, there is a rising tide of enthusiasm for reconsidering PCFs as a medium for reconfigurable data transmission in the future [33]. For these kinds of tasks, PCFs with a big mode area work well. Even if there are papers that deal with this matter, there are additional problems associated with the design of large mode area PCFs (LMA-PCFs).

III. PROPERTIES AND LOSS CALCULATION OF PHOTONIC CRYSTAL FIBER (PCF)

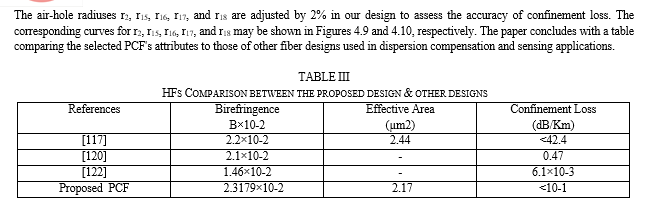
Achieving excellent properties in birefringence [61-69], dispersion [70-78], single polarization single mode [79-80], nonlinearity [81], and effective mode area [83-85], photonic crystal fibers (PCFs) [52-60] have been widely used in applications such as fiber sensors [86,87], fiber lasers [88,89], and nonlinear optics [42-45] for some time now. Ultrahigh birefringence and distinctive chromatic dispersion are two optical features of PCFs that have been the subject of several research articles; they are almost difficult for standard optical fibers to achieve. Optical fiber communications, filters, sensors, lasers, and more may all benefit from optical fibers having a high birefringence.

V. ACKNOWLEDGMENT

This research can be extended to design PCF using circular cladding for octagonal and decagonal design and artificially defected core PCFs as they offer a wide wavelength range of single-mode operation, controllable effective modal area tailorable dispersion, high birefringence and controllable nonlinearity.

Conclusion

To summarize, a polarization-maintaining fiber and telecommunication band PCF with a circular form that has been intentionally adjusted to assure strong birefringence and low confinement loss has been presented. The numerical findings show that the suggested design has a strong birefringence of 2.3179×10-2 and a low confinement loss of roughly less than 10-1 (dB/km), making it a promising choice for use in the telecommunication window design\'s fiber optic communication connection. As a result of their wide wavelength range of single-mode operation, controllable effective modal area, tailorable dispersion, high birefringence, and controllable nonlinearity, this study can be expanded to design PCFs with circular cladding for octagonal and decagonal designs, as well as with artificially defected core PCFs. The suggested structure is difficult to fabricate due to the usage of several kinds of air holes, including elliptical air, in this thesis. Therefore, finding the best fabrication for sensing and broadband dispersion correction will be the next step. once again, the fiber\'s splice loss and bending loss, which are essential for certain applications, are not taken into account in this study. Thus, more research is necessary to quantify the splice loss and bending loss and find a way to compensate for these. once again, despite significant efforts to improve birefringence, the confinement loss remains rather high. the confinement loss should be minimized to the greatest extent feasible.

References

[1] Knight, J.C., T. A. Birks, P. S. J. Russell, and D. M. Atkin, “Allsilicasinglemode optical fiber with photonic crystal cladding,\" Opr. Lett., Vol. 21, 15471549, 1996. [2] Birks, T. A., J. C. Knight, and P. S. J. Russel, “Endlessly singlemode photonic crystal fiber,\" Opt. Lett., Vol. 22, 961-963, 1997. [3] Knight, J. C., J. Broeng, T. A. Birks, and P. S. J. Russell, “Photonic band gap guidance in optical fibers,\" Science, Vol. 282, 1476-1478, 1998. [4] Knight, J.C. and P. S. J. Russell, “Photonic crystal fibers: New way to guide light,\" Science, Vol. 296, 276-277, 2002. [5] Knight, J. C. “Photonic crystal fibers,\" Nature, Vol. 424, 847-851, 2003. [6] J. A. Buck, Fundamentals of Optical Fibers, John Wiley & Sons Inc., USA, 2™ Edition, 2004. [7] S. V. Kartalopoulos, DWDM Networks, Devices, and Technology, John Wiley & Sons Inc., USA, 2003. [8] J. Hecht, Understanding Fiber Optics, Prentice Hall, USA, 3rd Edition, 1999. [9] E. Udd, Fiber Optic Sensors, John Wiley & Sons Inc., USA, 1991. [10] G.P. Agrawal, Nonlinear Fiber Optics, Academic Press, USA, 2nd Edition, 1995. [11] G.P. Agrawal, Fiber-Optic Communication Systems, John Wiley & Sons Inc., USA, 2nd Edition, 1997. [12] G.P. Agrawal, Fiber-Optic Communication Systems, John Wiley & Sons Inc., USA, 3rd Edition, 2002. [13] T. A. Birks, J. C. Knight, and P. St. J. Russell, “Endlessly single-mode photonic crystal fiber,” Optics Letters, vol. 22, no. 13, pp. 961-963, July 1997. [14] P. Petropoulus, T. Monro, W. Berlardi, K. Furusawa, J. Lee, and D. Richardson, “2R regenerative all-optical switch based on a highly nonlinear holey fiber,” Optics Letters, vol. 26, pp. 1233-1235, 2001. [15] M. Y. Chen, “Polarization and leakage properties of large-mode-area micro structured-core optical fibers,” Optics Express, vol. 15, no. 19, pp. 1249812507, 2007. [16] A. Ferrando, E. Silvestre, P. Andres, J. Miret, and M. Andres, “Nearly zero ultra-flattened dispersion in photonic crystal fibers,” Optics Letters, vol. 25, pp. 790-792, 2000. [17] J.C. Knight, T. A. Birks, P. St. J. Russel, and D. M. Atkin, “All-silica single-mode optical fiber with photonic crystal cladding,” Optics Letters, vol. 21, no. 19, pp. 1547-1549, 1996. [18] J.C. Knight, T. A. Birks, D. M. Atkin, and P. St. J. Russell, “Pure silica singlemodefibre with hexagonal photonic crystal cladding,” Optical Fiber Communication Conference, vol. 2, pp. 305-330, 1999. [19] J. Broeng, S. Barkou, A. Bjarklev, J. C. Knight, T. A. Birks, and P. St. J. Russell, “Highly increased photonic band gaps in silica/air structures,” Optics Communications, vol. 156, pp.240-244, 1998. [20] B. Kuhlmey, G. Renversez, and D. Maystre, “Chromatic dispersion and losses of microstructure optical fibers,” Applied Optics, vol. 42, no. 4, pp. 634-639, Feb. 2003. [21] G. Renversez, B. KuhImey, and R. McPhedran, “Dispersion management with microstructured optical fibers: ultra-flattened chromatic dispersion with low losses,” Optics Letters, vol. 28, no. 12, pp. 989-991, 2003. [22] K. Saitoh, M. Koshiba, T. Hasegawa, and E. Sasaoka, “Chromatic dispersion control in photonic crystal fibers: application to ultra-flattened dispersion,” Optics Express, vol. 11, no. 8, pp. 843-852, 2003. [23] F. Poletti, V. Finazzi, T. Monro, N. Broderick, V. Tse, and D. Richardson, “Inverse design and fabrication tolerances of ultra-flattened dispersion holey fibers,” Optics Express, vol. 13, no. 10, pp. 3728-3736, May 2005. [24] F. Poli, A. Cucinotta, S. Selleri, and A. Bouk, “Tailoring of Flattened dispersion in highly nonlinear photonic crystal fibers,” IEEE Photonics Technology Letters, vol. 16, no. 4, pp. 1065-1067, 2004. [25] K. Saitoh, and M. Koshiba, “Highly nonlinear dispersion-flattened photonic crystal fibers for supercontinuum generation in the telecommunication window,” Optics Express, vol. 12, pp.2027-2032, 2004. [26] T. A. Birks, J. C. Knight, and P. St. J. Russell, “Endlessly single-mode photonic crystal fiber,” Optics Letters, vol. 22, no. 13, pp. 961-963, 1997. [27] K. Kaneshima, Y. Namihira, N. Zou, H. Higa, and Y. Nagata, “Numerical investigation of octagonal photonic crystal fibers with strong confinement field”, IEICE Transactions on Electronics, vol. E89-C, no. 6, pp. 830-837, June 2006. [28] A. Ortigosa-Blanch, J. C. Knight, W. Wadsworth, J. Arriaga, B. Mangan, T. A. Birks, and P. St. J. Russell, “Highly birefringent photonic crystal fibers,” Optics Letters, vol. 25, pp.1325-1327, 2000. [29] H. Ademgil, S. Haxha, “Highly Birefringent photonic crytal fibers with ultralow chromatic dispersion and low confinement losses,” J. Lightwave Technology, vol. 26, pp. 441-448, 2008. [30] K. Tajima, J. Zhou, K. Nakajima, and K. Sato, “Ultralow loss and long length photonic crystal fiber,” J. Lightwave Technology, vol. 22, pp. 7-10, 2004. [31] J. Zhou, K. Tajima, K. Nakajima, K. Kurokawa, C. Fukai, T. Maisui, and J. Sankawa, “Progress on low loss photonic crystal fiber,” Optical Fiber Technology, vol. 11, pp. 101-106, 2005. [32] P. Roberts, F. Couny, H. Sabert, B. Mangan, D. Williams, L. Farr, M. Mason, A Tomlinson, T. A. Birks, J. C. Knight, and P. St. J. Russell, “Ultimate low loss of hollow-core photonic crystal fibers,” Optics Express, vol.13, no.1, pp. 236-244, Jan. 2005. [33] N. J. Florous, K. Saitoh, and M. Koshiba, “The role of artificial defects for engineering large effective mode area, flat chromatic dispersion, and low leakage losses in photonic crystal fibers: towards high-speed reconfigurable transmission platforms,” Optics Express, vol. 14, pp. 901-913, Jan. 2006. [34] P. St. J. Russell, “History and future of photonic crystal fibers,” Optical Fiber Communication Conference/ National Fiber Optic Engineers Conference (OFC/NFOEC) 2009, OTuC1, San Diego, CA, USA, March 22-26, 2009. [35] P. St. J. Russell, “Photonic crystal fibers: A historical account,” IEEE LEOS Newsletter, vol. 21, pp. 11-15, Oct. 2007. [36] S.M.A. Razzak, Y. Namihira, ‘’Tailoring dispersion and confinement losses of photonic crystal fibers using hybrid cladding’, J. Light w. Technol. 26 (2008) 1909~ 1914. [37] Patrice Megrett, Sebatien Bette, Cathy Crunelle, Christophe Caucheteur, “Fiber Bragg Gratings: Fundamentals and Applications,” 3rd May 2007. [38] R. Buczynski, Information Optics Group, Faculty of Physics, Warsaw University, Pasteura 7, 02- 093 Warsaw, Poland, “Photonic Crystal Fibers”, ActaPhysicaPolonica A, Vol. 106 (2004), No.2 [39] J. Ju, W. Jin, M.S. Demokan, Properties of a highly birefringent photonic crystal fiber, [EEE Photon. Technol. Lett. 15 (2003) 1375-1377. [40] J.C. Knight, T.A. Birks, P.S.J. Russell, J.P. Sandro, Properties of photonic crystal fiber and the effective index model, J. Opt. Soc. Am. A 15 (1998) 748-752. [41] T. Matsui, J. Zhou, K. Nakajima, I. Sankawa, Dispersion-flattened photonic crystal fiber with large effective area and low confinement loss, J. Lightw. Technol. 23 (2005) 4178-4183. [42] Y.N. Zhang, Design and optimization of high birefringence low loss photoniccrystal fiber with two zero dispersion wavelengths for nonlinear effects, Appl.Opt. 50 (2011) E125—-E130. [43] Yuh-Sien SUN, Yuan-Fong CHAU_, Han-Hsuan YEH, and Din Ping TSAI,”’ Highly Birefringent Index-Guiding Photonic Crystal Fiber with Squeezed Differently Sized Air-Holes in Cladding’’, Japanese Journal of Applied Physics Vol. 47, No. 5, 2008, pp. 3755-3759. [44] Md. Samiul Habib, K. M. Nasim, Md. Selim Habib, Md. Imran Hasan, RedwanAhmad,’’Relative dispersion slope matched dispersion compensating highly birefringent spiral microstructure optical fibers using defected core’’, Optical Engineering 52(9), 096110 (September 2013). [45] M Selim Habib, M.MejbaulHaqueb, M. Samiul Habiba, M.I. Hasanc, M. ShaifurRahmanb, S.M.A. Razzaka, ‘’Polarization maintaining holey fibers for residual dispersion compensation over S + C + L wavelength bands’’, at Science Direct. [46] J. A. Buck, Fundamentals of Optical Fibers, John Wiley & Sons Inc., USA, 2nd Edition, 2004. [47] S. V. Kartalopoulos, DWDM Networks, Devices, and Technology, John Wiley &Sons Inc., USA, 2003. [48] J. Hecht, Understanding Fiber Optics, Prentice Hall, USA, 3rd Edition, 1999. [49] ArismarCerqueira S. Jr., F. Luan, C. M. B. Cordeiro , A. K. George and J. C. Knight, “Hybrid Photonic Crystal Fiber”, OPTICS EXPRESS 92623, vol. 14, No. 2 , January 2006 . [50] Martin Hermatschweiler, Alexandra Ledermann, Geoffrey A. Ozin, Martin Wegener and Georg von Freymann, “Fabrication of Silicon Inverse Woodpile Photonic Crystals”, Advanced Functional Materials, pp.2273–2277, 2007. [51] P. St. J. Russell, “History and future of photonic crystal fibers,” Optical Fiber Communication Conference/ National Fiber Optic Engineers Conference (OFC/NFOEC)2009, OTuC1, San Diego, CA, USA, March 22-26, 2009. [52] Rodrigo Amezcua Correa, “Development of Hollow-core Photonic Bandgap Fibers Tree of Surface Modes”, University of Southampton, Optoelectronics research center, March 2009. [53] Gelin Zhang, Fengfei Xing, Peiguang Yan, Huifeng Wei, Huiquan Li, Shisheng Huang, Rongyong Lin and Kangkang Chen, “Double Cladding Seven-Core Photonic Crystal Fiber”, Optics and Photonics Journal, pp. 47-49, 2013 [54] Shizhuo Yin and Ruyan Guo, “Advances in Materials and Innovations in Device Applications VIII ”, SPIE Proceedings, 9200A, September 5, 2014. [55] T.S. Sainia, A. Bailib, A. Kumara, R. Cherifb, M. Zghalb and R.K. Sinhaa, “Design and Analysis of Equiangular Spiral Photonic Crystal Fiber for mid-infrared Supercontinuum Generation”, Journal of Modern Optics, vol. 62, Issue 19, pages 1570-1576, June 9,2015. [56] Pascal Dupriez and Claude Aguergarary, “Advances in Integration of Photonic Crystal Fibers in High-power Fiber Laser”, Workshop on Specialty Optical Fibers and Their Applications OSA Technical Digest (online) (Optical Society of America, 2015), paper WT2A.2 [57] Shen G.-F., X.-M. Zhang, H. Chi, and X.-F. Jin, “Microwave/millimeter-wave generation using multi-wavelength photonic crystal fiber brillouin laser,\" Progress In Electromagnet ics Research, Vol. 80, 307-320, 2008. ‘ [58] Nozhat N. and N. Granpayeh, “Specialty fibers designed by photonic crystals,\" Progress In Electromagnetics Research, Vol. 99, 225-244, 2009. [59] Wu J.-J., D. Chen, K.-L. Liao, T.-J. Yang, and W.-L. Ouyang, “The optical properties of bragg fiber with a fiber core of 2dimension elliptical-hole photonic crystal structure,\" Progress In Electromagnetics Research Letters, Vol. 10, 87-95, 2009. [60] Chau Y.-F., C.-Y. Liu, H.-H. Yeh, and D. P. Tsai, “A comparative study of high birefringence and low confinement loss photonic crystal fiber employing elliptical air holes in fiber cladding with tetragonal lattice,\" Progress In Electromagnetics Research B, Vol. 22, 39-52, 2010. [61] Ortigosa-Blanch, A., J. C. Knight, W. J. Wadsworth, J. Arriaga, B. J. Mangan, T. A. Birks, and P. S. J. Russel, “Highly birefringent photonic crystal fibers,\" Opt. Lett., Vol. 25, 1325-1327, 2000. [62] Ademgil, H. and S. Haxha, “Highly birefringent photonic crystal fibers with ultralow chromatic dispersion and low confinement losses,\" J. Lightwave Technol., Vol. 26, 441-448, 2008. [63] Hansen, T. P., J. Broeng, S. E. B. Libori, E. Knudsen, A. Bjarklev, J. R. Jensen, and H. Simonsen, “Highly birefringent index-guiding photonic crystal fibers,\" IEEE Photon. Technol. Lett., Vol. 13, 588-590, 2001. [64] Sapulak, M., G. Statkiewicz, J. Olszewski, T. Martynkien, W. Urbanczyk, J. Wojcik, M. Makara, J. Klimek, T. Nasilowski, F. Berghmans, and H. Thienpont, “Experimental and theoretical investigations of birefringent holey fibers with a triple defect,\" Appl. Opt., Vol. 44, 2652-2658, 2005. [65] Anthkowiak, M., R. Kotynski, T. Nasilowski, P. Lesiak, J.Wojcik, W. Urbanczyk, f. Berghmans, and H. Thienpont, “Phase and group modal birefringence of tripledefect photonic crystal fibers,\" J. Opt. A: Pure Appl. Opt., Vol. 7, 763-766, 2005. [66] Chen, D. and L. Shen, “Highly birefringent elliptical-hole photonic crystal fibers with double defect,\" J. Lightw. Technol., Vol. 25, 2700-2705, 2007. [67] Steel, M. J. and R. M. Osgood, “Elliptical-hole photonic crystal fibers,\" Opt. Lett., Vol. 26, 229-231, 2001. [68] Steel, M. J. and R. M. Osgood, “Polarization and dispersive properties of ellipticalhole photonics crystal fibers,\" J. Lightwave Technol., Vol. 19, 495-503, 2001. [69] Yue, Y., G. Kai, Z. Wang, T. Sun, L. Jin, Y. Lu, C. Zhang, J. Liu, Y. Li, Y. Liu, S. Yuan, and X. Dong, “Highly birefringent elliptical-hole photonic crystal fiber with squeezed hexagonal lattice,\" Opt. Lett., Vol. 32, 469-471, 2007. [70] Chen, D. and L. Shen, “Ultrahigh birefringent photonic crystal fiber with ultralow confinement loss,\" IEEE Photon. Technol. Lett., Vol. 19, 185-187, 2007. [71] Agrawal, A., N. Kejalakshmy, J. Chen, B. M. A. Rahman, and K. T. V. Grattan, “Golden spiral photonic crystal fiber: Polarization and dispersion properties,\" Opt. Lett., Vol. 33, 2716-2718, 2008. [72] Shen, L. P., W. P. Huang, and S. S. Jian, “Design of photonic crystal fibers for dispersion related applications,\" J. Light wave Technol., Vol. 21, 1644-1651, 2003. Ferrando, A., E. Silvestre, J. J. Miret, and P. Andres, “Nearly zero ultra-flattened dispersion in photonic crystal fibers,\" Opt. Lett., Vol. 25, 790-792, 2000. [73] Ferrando, A., E. Silvestre, P. Andres, J. Miret, and M. Andres,”Designing the properties of dispersion-flattened photonic crystal fibers,\" Opt. Express, Vol. 9, 687697, 2001. [74] Saitoh, K., M. Koshiba, T. Hasegawa, and E. Sasaoka, “Chromatic dispersion control in photonic crystal fibers: Application to ultra-flattened dispersion,\" Opt. Express, Vol. 11, 843-852, 2003. [75] Saitoh, K., M. Koshiba, T. Hasegawa, and E. Sasaoka, “Chromatic dispersion control in photonic crystal fibers: Application to ultra-flattened dispersion,\" Opt. Express, Vol. 11, 843-852, 2003. [76] Glernome, F., J.-L. Auguste, and J.-M. Blondy, “Design of dispersion-compensating fibers based on a dual-concentric-core photonic crystal fiber,\" Opt. Lett., Vol. 29, yM5-2T27, 2004. [77] Hutunen, A. and P. TAormAa, “Optimization of dual-core and microstructure fiber geometries for dispersion compensation and large mode area,\" Opt. Express, Vol. 13, 627-635, 2005. [78] Varshney, S. K., T. Fujisawa, K. Saitoh, and M. Koshiba, “Design and analysis of a broadband dispersion compensating photonic crystal fiber Raman amplifier operating in S-band,” Opt. Express, Vol. 14, 3528-3540, 2006. [79] Yang, S., Y. Zhang, X. Peng, Y. Lu, S. Xie, J. Li, W. Chen, Z. Jiang, J. Peng, and H. Li, “Theoretical study and experimental fabrication of high negative dispersion photonic crystal fiber with large area mode field,\" Opt. Express, Vol. 14, 3015-3023, 2006. [80] Ju, J., W. Jin, and M. S. Demokan, “Design of single-polarization single mode photonics crystal fibers,\" J. Light wave Technol., Vol. 24, 825-830, 2001. [81] Saitoh, K. and M. Koshiba, “Single-polarization single-mode photonic crystal fibers,\" IEEE Photon. Technol. Lett., Vol. 15, 1384-1340, 2003. [82] Kubota, H., S. Kawanishi, S. Koyanagi, M. Tanaka, and S. Yamaguchi, “Absolutely single polarization photonic crystal fiber,\" IEEE Photon. Technol. Lett., Vol. 16, 182-184, 2004. [83] Knight, J. C. and D. V. Skryabin, “Nonlinear waveguide optics and photonic crystal fibers,\" Opt. Express, Vol. 15, 15365-15376,2007. [84] Mortensen, N. A., M. D. Nielsen, J. R. Folkenberg, A. Petersson, and H. R. Simonsen, “Improved large-mode-area endlessly singlemode photonic crystal fibers,\" Opt. Lett., Vol. 28, 393-395, 2003. [85] Limpert, J., T. Schreiber, S. Nolte, H. Zellmer, T. Tunnermann, R. [liew, F. Lederer, [86] J. Broeng, G. Vienne, A. Petersson, and C. Jakobsen, “High-power air-clad largemode-area photonic crystal fiber laser,\" Opt. Express, Vol. 11, 818-823, 2003. [87] Folkenberg, J., M. Nielsen, N. Mortensen, C. Jakobsen, and H. Simonsen,“Polarization maintaining large mode area photonic crystal fiber,\" Opt. Express, Vol. 12, 956-960, 2004. [88] Dobb, H., K. Kalli, and D. J. Webb, “Temperature-insensitive long period grating sensors in photonic crystal fibre,\" Eletron. Lett., Vol. 40, 657-658, 2004. [89] Dong, X. and H. Y. Tam, “Temperature-insensitive strain sensor with polarizationmaintaining photonic crystal fiber based on Sagnac interferometer,\" Appl. Phys. Lett., Vol. 90, 151113, 2007, [90] Wadsworth, W. J., J.C. Knight, W. H, Reewes, P. S. J. Russell, and J. Arriaga, “Yb+3 doped photonic crystal fibre laser,\" Eletron. Lett., Vol. 36, 1252-1253, 2000. [91] Liu, X., X. Zhou, X. Tang, J. Ng, J. Hao, T. Chai, E. Leong, and C. Lu, “Swithable and tunable multi-wavelength erbium-doped fiber laser with fiber Bragg grating and photonic crystal fiber,\" IEEE Photon. Technol. Lett., Vol. 17, 1626-1628, 2005. [92] Chen, D., “Stable multi-wavelength erbium-doped fiber laser based on photonic crystal fiber Sagnac loop filter,\" Laser Phys. Lett., Vol. 4, 437-439, 2007. [93] Broderick, N. G. R., T. M. Monro, P. J. Bennett, and D. J. Richardson, “Nonlinearity in holey optical fibers: Measurement and future opportunities,\" Opt. Lett., Vol. 24, 1395-1397, 1999. [94] Zhu, Z. and T. G. Brown, “Experimental studies of polarization properties of super continua generated in a birefringent photonic crystal fiber,\" Opt. Express, Vol. 12, 791-796, 2004. [95] Zhu, Z. and T. G. Brown, “Polarization properties of super continuum spectra generated in birefringent photonic crystal fibers,\" J. Opt. Soc. Am. B, Vol. 21, 249257, 2004. [96] Zhu, Z. and T. G. Brown, “Polarization properties of super continuum spectra generated in birefringent photonic crystal fibers,\" J. Opt. Soc. Am. B, Vol. 21, 249257, 2004. [97] Dudley, J. M. and J. R. Taylor, “Ten years of nonlinear optics in photonic crystal fiber,\" Nature Photonics, Vol. 3, 85-90, 2009. [98] A. Bjarklev, J. Broeng, A. S. Bjarklev, Photonic Crystal Fibers, Kulawer Academic Press, USA, 2003. [99] F, Poli, A. Cucinotta, S. Selleri, and A. Bouk, “Tailoring of Flattened dispersion in highly nonlinear photonic crystal fibers,” IEEE Photonics Technology Letters, vol. 16, no. 4, pp. 1065-1067, 2004. [100] Broeng, D. Mogilevstev, S.E. Barkou, A. Bjarklev, Photonic crystal fibers: a newclass of optical waveguides, Opt. Fiber Technol. 5 (1999) 305-330. [101] T.A. Birks, J.C. Knight, B.J.P. Mangan, St.J. Russell, Photonic crystal fibers: anendless variety, IEICE Trans. Electron. E84-C (2001) 585-592. [102] J.C. Knight, T.A.P. Birks, St.J. Russell, D.M. Atkin, All-silica single-modeoptical fiber with photonic crystal cladding, Opt. Lett. 21 (1996)1547-1549. [103] L. Dong, H.A. McKay, L. Fu, All glass endless single mode photonic crystal fibers,Opt. Lett. 33 (2008) 2440—2442. [104] J. Li, J. Wang, Y. Cheng, et al., Novel large mode area photonic crystalfibers with selectively material filled structure, Opt. Laser Technol. 48 (2013)375—380. [105] H. Ademgil, S. Haxha, Endlessly single mode photonic crystal fiber withimproved effective mode area, Opt. Commun. 285 (2012) 1514-1518. [106] F. Begum, Y. Namiuhira, S.M. Abdur Razzak, et al., Design and analysis of novelhighly nonlinear photonic crystal fibers with ultra-flattened chromatic dispersion, Opt. Commun. 282 (2009) 1416-1421. [107] Y. Liu, J.Y. Wang, Y.Q. Li, R. Wang, J.-H. Li, X.G. Xie, A novel hybrid photonic crystaldispersion compensating fiber with multiple windows, Opt. Laser Technol. 44(2012) 2076—2079. [108] B. Hu, M. Lu, W. Li, et al., High birefringent rhombic hole photonic crystal fibers,Appl. Opt. 49 (2010) 6098-6101. [109] R. Bhattacharya, S. Konar, extremely large birefringence and shifting of zerodispersion wavelength of photonic crystal fibers, Opt. Laser Technol. 44 (2012)2210—2216. [110] J. Knight, T. Birks, R. Cregan, P. Russell, and J. Sandro, “Large mode area photonic crystal fiber,” Electron. Lett., vol. 34, no. 13, pp. 1347—1348, Jun. 1998. [111] M. Eguchi, Y. Tsuji, Single-mode single-polarization holey fiber usinganisotropic fundamental space-filling mode, Opt. Lett. 32 (2007) 2112-2114. [112] DJ. Juan Hu, P.P. Shum, C. Lu, G. Ren, Dispersion-flattened polarizationmaintaining photonic crystal fiber for nonlinear application, Opt. Commun.282(2009) 4072—4076. [113] S. Zuoming, S. Ningfang, J. Jing, S. Jingming, M. Pan, Low loss fusion splicing polarization maintaining photonic crystal fiber and conventional polarizationmaintaining fiber, Opt. Fiber Technol. 18 (2012) 452-456. [114] L. An, Z. Zheng, Z. Li, T. Zhou, J. Cheng, Ultra-wideband single polarization single mode high nonlinearity photonic crystal fiber, Opt. Commun. 282 (2009)32663269. [115] S.-G. Lee, S.D. Lim, K. Lee, S.B, Lee, Single polarization single mode photonic crystal fiber based on index matching coupling with a single silica material,Opt. Fiber Technol. 17 (2011) 36—40. [116] Y.N. Zhang, Design and optimization of high birefringence low loss photoniccrystal fiber with two zero dispersion wavelengths for nonlinear effects, Appl.Opt. 50 (2011) E125—-E130. [117] Z. Xingtao, Z. Guiyao, L. Shuguang, L. Zhaolun, W. Dongbin, H. Zhiyun, et al., photonic crystal fiber for dispersion compensation, Appl. Opt. (2008)5190. [118] S.K. Varshney, T. Fujisawa, K. Saitoh, M. Koshiba, Design and analysis of a broadband dispersion compensating photonic crystal fiber Raman amplifier ‘ operating in S-band, Opt. Express (2006) 3528 [119] Md. Samiul Habib, K. M. Nasim, Md. Selim Habib, Md. Imran Hasan, Redwan Ahmad ‘Relative dispersion slope matched dispersion compensating highly birefringent spiral microstructure optical fibers using defected core’ Optical Engineering 52(9), 096110 (September 2013) [120] Rui Haoa,b, Zhiquan Lib, HuijingDua, LiyongNiub ‘’Squeezed hexagonal highly birefringent photonic crystal fiber with low effective modal area.” [121] M.Samiul Habiba, M. Selim Habiba, M.I. Hasanb, S.M.A. Razzaka, M.A. Hossainc, Y.Namihiraca Polarization maintaining large nonlinear coefficient photonic crystalfibers using rotational hybrid cladding. [122] K. Prabua,? , R. Malavikab, highly birefringent photonic crystal fiber with hybrid cladding.”Optical Fiber Technology.,Vol.47. January 2019. [123] M. Selim Habiba, M. MejbaulHaqueb, M. Samiul Habiba, M.I. Hasanc, M. ShaifurRahmanb, 8.M.A. Razzaka ‘’Polarization maintaining holey fibers for residual dispersion compensation over S + C + L wavelength bands’’ [124] C. Gui, J. Wang, Elliptical-spiral photonic crystal fibers with wideband high birefringence, large nonlinearity, and low dispersion, IEEE Photon. J. 4 (2012)

Copyright

Copyright © 2024 Ramin Chapa Rumpa, Abu Zafur , Md Ratul Hasan, Imtiaz Ahamed Apon, Md. Imran Badsha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.